Matlab在绘制两相互垂直斜锯齿振动与简谐振动合成运动轨迹图形的应用
刘会玲 王小克 牛海波 赵丽华 胡龄之 雷玉明
(西安交通大学城市学院,陕西 西安 710018)
1 提出问题
在振动学中,相互垂直的两简谐振动合成时,如果两简谐振动的频率相同,则可形成稳定的椭圆曲线,极端条件为圆和直线;而当两相互垂直的简谐振动频率不同时,合成运动比较复杂,其运动轨迹一般不闭合,但当两分振动频率成简单的整数比时,其合成运动的轨迹则为封闭曲线,因由法国物理学家李萨如发现而得名,故称为李萨如图形(Lissajous figure)。而相互垂直的两任意振动的合成运动轨迹图形,则称为广义李萨如图形。
在学习物理学的波动理论和大学物理实验的振动合成时,都接触过李萨如图形,关于李萨如图形的几何特征(大小、结构、对称性、歪曲方向和歪曲程度等),以及李萨如图形的合成轨迹受多个因素(两个分振动的频率比、初相位、相位差等)的影响规律,书中也有很好的归纳和总结,然而,这些结论比较抽象,不易理解和掌握;虽然课堂上和实验室中也有很多演示李萨如图形的方法,比如物理课堂上用激光来演示李萨如图形,实验室中用示波器来显示,但是一般都需要比较多的仪器来配合完成,而且演示的效果及种类受仪器的限制,很难满足实际的需求。
如果能够用软件绘制出多种情况下的李萨如图形,就可以直观体现出李萨如图形的几何特征,以及上述因素对轨迹合成的影响,从而便于学生比较分析,进行深入理解和认识,为教学和测量提供有效的手段。
本文主要介绍利用MatLab编程绘制广义李萨如图形,主要绘制不同参数下的两相互垂直的斜锯齿振动与余弦振动的合成运动轨迹图形,锯齿振动也是一种简单的周期性振动,两相互垂直的锯齿振动与简谐振动的合成运动轨迹图形,也可以用两相互垂直简谐振动的合成运动轨迹图形的方法讨论。此类合成运动轨迹图形比较复杂,而MatLab编程绘制这类图形快速、灵活且准确度高,从而体现出其在绘图方面的强大功能。
2 用Matlab编程绘制 两相互垂直斜锯齿振动与简谐振动合成运动轨迹
2.1 锯齿函数的定义
相位φ的锯齿函数S(φ) 定义如下:
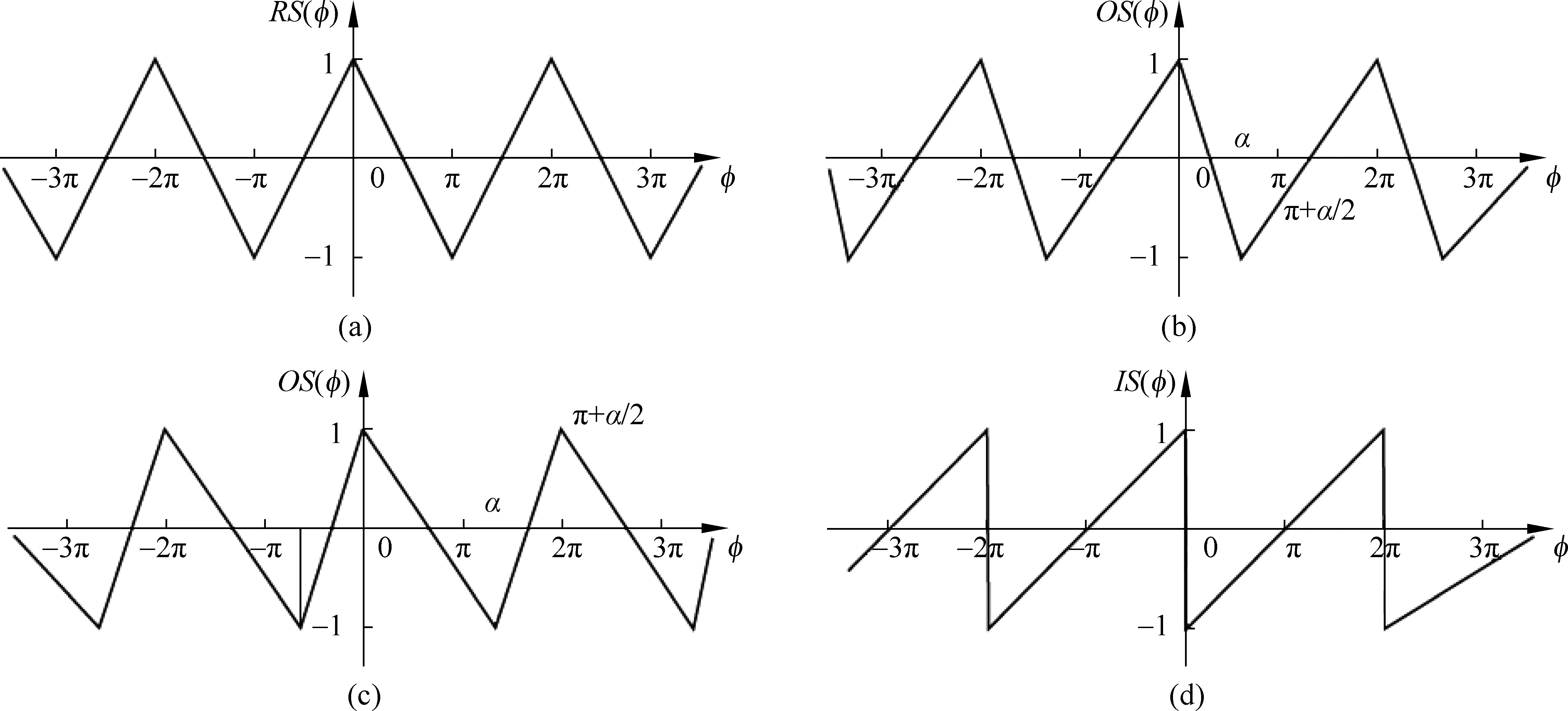
图1 S(φ) 函数曲线(a) α=π; (b) 0<α<π; (c) π<α<2π; (d) α=0
(1)
在式(1)给定的锯齿函数中,α为常数。图1是S(φ) 的函数曲线,其中横坐标代表相位φ,纵坐标代表函数S(φ)(RS(φ)、OS(φ) 和IS(φ)),这3类函数定义见下面几段文字。
习惯上,把α等于π的锯齿函数,称为正锯齿函数,记作RS(φ),对应的曲线叫做三角波,见图1(a);
把α等于零的锯齿函数,称为理想锯齿函数,记作IS(φ),对应的曲线见图1(d);
把α不等于零和π的锯齿函数,统称为斜锯齿函数,记作OS(φ),对应的曲线如图1(b)和1(c)。
它们所描述的振动,分别称为正锯齿振动、理想锯齿振动和斜锯齿振动。
2.2 两相互垂直斜锯齿振动与余弦振动的合成运动
设x分振动为斜锯齿振动,y分振动为余弦振动,合成运动的方程为
(2)
2.3 绘制上述合成运动轨迹图形的程序设计
Matlab中的M文件的语法与C语言类似,是一种程序化的编程语言,同时也是一种解释性的编程语言,即逐行解释运行程序,程序更容易调试。它只是一个简单的ASCII码文本文件,语法比一般的高级语言都要简单,与数学语言比较接近,更容易掌握和理解。
以下是用MatLab编程绘制的不同频率比(为有理数)、不同相位差的两相互垂直斜锯齿振动与余弦振动合成运动轨迹图形程序的完整代码:
clc;clear;
fx=1;
f0=0;
ffx=0:0.01:(2*pi);
y1=zeros(size(ffx));
N=length(ffx);
for k=1:N
x=floor((ffx(k)-f0)/(fx*pi))/2;
if(x==floor(x))
y1(k)=2*(2*x+f0/(fx*pi))+1-2*ffx(k)/(fx*pi);
else
y1(k)=-1+2*(ffx(k)-(2*x)*pi*fx)/(fx*pi)-2*f0/(fx*pi);
end
end
fy=1;
fy0=0;
ffy=0:0.01:(2*pi);
y2=zeros(size(ffy));
N=length(ffy);
for k=1:N
x=floor((ffy(k)-fy0)/(fy*pi))/2;
if (x==floor(x))
y2(k)=2*(2*x+fy0/(fy*pi))+1-2*ffy(k)/(fy*pi);
else
y2(k)=-1+2*(ffy(k)-(2*x)*pi*fy)/(fy*pi)-2*fy0/(fy*pi);
end
end
y3=cos(ffy+fy0);
plot(y3,y1,'k');
2.4 上述合成运动轨迹图形结果
下面是不同频率比、不同相位差的两相互垂直斜锯齿振动与余弦振动合成运动轨迹图形的举例图像,见图2,以便学生对比研究。
3 应用上述Matlab程序绘制并分析两相互垂直振动的合成运动轨迹图形的分振动频率比规律
3.1 两相互垂直简谐振动合成运动轨迹图形的分振动频率比规律
在李萨如图形中,当两相互垂直的简谐振动的频率比为整数比时,若设Y方向振动的频率为fY,X方向振动的频率为fX,设纵直线与合成运动轨迹的切点数为nY,横直线与合成运动轨迹的切点数为nx,则Y方向振动与X方向振动的频率比规律为:fY:fX=nx:nY,或者说两相互垂直的简谐振动的周期比为整数比时,则XY方向振动的周期比等于图形中横纵切点数目比。
当两相互垂直简谐振动频率比一定时,李萨如图形随相位Φ变化周期性地变化,若Φ取一个周期2π内的一系列适当值,作出一组李萨如图,称为系列图。
系列图可以形象地表示出分振动频率比与横纵切点数的关系,及不同频率比时的李萨如图形随Φ变化的规律,同时还可根据系列图推想出该频率比的所有李萨如图形的性状。图3是几种不同频率比的两相互垂直简谐振动合成运动轨迹系列图。

图2 两相互垂直的斜锯齿振动与余弦振动的合成运动轨迹图形举例图

图3 几种不同频率比的两相互垂直的简谐振动合成运动轨迹系列图

图4 几种不同频率比的两相互垂直的正锯齿振动与余弦振动的合成运动轨迹系列图
从系列图还可以看出,李萨如图形性状与Φ值和频率比有关,与频率比对应的两个分振动fY、fX的大小没有直接关系。
3.2 两相互垂直的正锯齿振动与余弦振动合成运动轨迹图形、两相互垂直正锯齿振动合成运动轨迹图形的分振动频率比规律
图4是几种不同频率比的 两相互垂直的正锯齿振动与余弦振动的合成运动轨迹系列图。图5是几种不同频率比的 两相互垂直正锯齿振动的合成运动轨迹系列图。
从图3、图4和图5可以看出,合成运动轨迹图形具有相似性,所以当两相互垂直的锯齿振动的频率比为整数比时,或者当两相互垂直的锯齿振动与简谐振动的频率比为整数比时,其分振动的频率比仍遵循两相互垂直的简谐振动合成运动轨迹图形的频率比规律。
3.3 两相互垂直锯齿、两相互垂直锯齿与简谐振动及两相互垂直简谐振动的合成运动轨迹图形的相似性
正锯齿函数曲线与余弦函数曲线除去连接两个时间相邻的极值点的函数曲线为直线段之外,正锯齿函数曲线与余弦函数曲线有许多共同之处。因此,两相互垂直的正锯齿振动的合成运动轨迹图形,或相互垂直的正锯齿振动与余弦振动的合成运动轨迹图形,与两相互垂直的余弦振动合成运动轨迹图形具有一定的相似性。

图5 几种不同频率比的两相互垂直的正锯齿振动的合成运动轨迹系列图
理想锯齿函数和斜锯齿函数的性质与余弦函数有较大的差别,但也有一些共同之处,它们都是相位和时间的周期函数,相位周期为2π,时间周期为1/f,在一个周期内,函数只有一个极大值和一个极小值,在时间相邻的正、负极值点之间,函数随自变量单调连续地变化,因此,两相互垂直的简谐振动的合成运动轨迹图形的很多规律,也适用于两相互垂直的理想锯齿(或斜锯齿)振动的合成运动轨迹图形,及相互垂直的理想锯齿(或斜锯齿)振动与简谐振动的合成运动轨迹图形。
4 总结
上面的程序具有通用性,只需要更改函数及参数,就可以绘制出各种情况的这类合成运动轨迹图形。利用Matlab编程还可以绘制高斯分布、麦克斯韦分布、电场分布、等势线分布、等厚干涉及干涉衍射图样等等。物理学是一门实验性很强
的科学,其理论是建立在实验的基础之上的,由于实验条件的限制,物理学中的许多内容无法在课堂上直接用实验来验证,使学生对理论的理解有一定的困难,而通过Matlab数值计算和图形模拟,能够把抽象复杂的物理概念和公式以更加直观的图形形式呈现出来,从而激发学生学习的兴趣,提高了教学质量。同时通过绘制出的图形,还可以进行很多方面的分析和研究,在解决实际问题时有着非常重要的作用。

