沙堆休止角与含水量关系探究
王涵斌 史鼎元 王文玲
(北京航空航天大学 1航空科学与工程学院; 2高等理工学院;3物理科学与核能工程学院,北京 100083)
颗粒休止角是在重力场中,颗粒在粉体堆积层的自由斜面上滑动时所受重力和粒子之间摩擦力达到平衡而处于静止状态下测得的最大角。它对泥石流预测与土壤结构稳定等问题的探索具有重要意义,日本学者Yoshioka N. 在研究地震中的土壤稳定性问题时就使用休止角作为土壤稳定性的力学指标[1]。
研究表明,影响休止角大小最为明显的因素是含水量[2]。自然世界中土壤颗粒的半径、形状、密度等性质相对稳定(不会受环境影响而急速改变),含水量则不同,它会受降水的影响在短时间显著变化,极大地改变土壤的力学性质。故含水量对土壤结构的影响既是很主要的,也具有很强的实际意义。因此本文将重点研究沙堆休止角随含水量的变化关系。但目前对于含水量与休止角的关系研究并不成熟。在《颗粒物质力学导论》[3]一书中,建立了含水量与颗粒间液桥力的大小关系,但是没有将含水量与休止角两个宏观量建立联系。 Cundall P.A.等人发表文章提出了离散元方法(discrete element method, DEM),这种方法的基本思想是把每个颗粒看作独立的微元,通过给定的相互作用力和边界条件,使用计算机蛮力迭代求解[4],这可以建立颗粒粘聚能量密度与休止角的关系,依旧没有将两个宏观量建立起联系。
在实验方面,本文搭建了合理限制自由度的休止角生成装置,并使用计算机视觉的处理方法,利用OpenCV这款开源的计算机视觉库,把图像的颜色转化成灰度值,将灰度值平均运算,进行平滑处理,剔除图像中不必要的信息。最后计算灰度变化梯度,因为沙堆的颜色和背景差异很大,梯度较大的地方可以推测为沙堆的轮廓。有了轮廓上每个点的坐标,就可以使用数学工具进行直线拟合,进而通过直线斜率得到角度大小。
我们的视觉处理方法可以准确地进行了休止角测量,由此可以得到可靠的含水量与休止角数据。在理论方面,初步构建了休止角-含水量数学模型,并给出了合理的物理解释。
1 实验设计
1.1 休止角生成的方法
常见的休止角生成方法有3种:注入法、排出法和倾斜法。注入法是在漏斗中添加粉体使之下落在承接台上形成锥体的方法,休止角为锥体侧面与地面夹角。排出法是使粉体从容器流出部分之后剩余粉体形成的凹陷的方法,休止角是凹陷面与水平面的夹角。倾斜法是在绕水平轴慢速回转的圆筒容器内加入1/2~1/3容积的粉体,当粉体的表面产生滑动时,测定其表面的倾角的方法。具体模式如图1所示。
3种方法中,排出法形成的休止角位于装置内部,不便于测量;倾斜法是动态过程实验装置较为复杂,休止角的生成角度误差较大。特别是不便于使用本实验的测量方法。因此,我们选择注入法。
1.2 实验仪器的搭建
传统的休止角生成和测量如图2所示[2、5]。由图2可以看到,此装置(图2(a)[2])有一些不足之处:第一,支架和漏斗的固定处可能存在转动自由度,使漏斗的出口方向和下面的承接台不完全垂直,造成误差。第二,漏斗的固定臂会因为漏斗重力的作用产生挠度与支端转角。第三,承接台不平也会影响到实验准确度。

图2 传统休止角测定仪模式图
针对上述3个问题,本文分别加以改进。
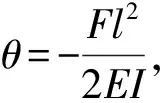

图3 实验仪器
1.3 测量方法设计
沙堆是一个三维锥体,不便于测量,因此可以通过拍照将其转化为二维。但是沙堆并不是标准锥体,图像边缘不是直线,人手工测量会有一定的主观性和不确定性,因此采用计算机视觉技术进行测量。OpenCV是一款开源成熟度的计算机视觉库,应用这个库,可以在照片上找出沙堆的轮廓,并把轮廓上点的坐标进行直线拟合,直线的斜率即对应休止角的正切值,这样就规避了人在测量非标准直线构成的夹角时的主观性。
在实际拍摄的时候,使用三脚架固定了镜头的位置,保持镜头和水平面垂直,且距离被测沙堆20cm左右。这样每次拍摄的位置固定,可以避免因为镜头倾斜或俯仰造成的误差。另外通过保持被测物体在照片中间等手段大大减少了手机镜头引起的镜头畸变或感光元件间隔不均匀造成的测量误差。
颗粒在下落过程中,使用漏斗上方固定的搅拌装置缓慢搅拌,这让颗粒流出漏斗后具有微小且随机的水平速度,保证了沙堆的形状是近似中心对称的,加上多次测量求平均值的处理,就可以消除因为拍摄位置固定而可能带来的系统误差。
为了在照片上找到轮廓,要在灰化的基础上采用Sobel算子进行梯度检测,这样有助于定位边界的位置和检测边缘,之后再使用模糊化处理通过灰度梯度的变化找到边界,就可以计算休止角的大小了。其完整的测量流程和各阶段效果如图4。

图4 测量流程
该程序能够十分准确地找到沙堆的边界,并且通过直线拟合推测休止角的大小,完全规避了人在测量中的主观性,测量十分准确。
另外,由于拍照通常是在手机上进行,但是程序的运行和调试使用电脑更加方便,为了弥合两者之间的矛盾,搭建了一个小服务器实现前后端架构。手机浏览器作为前端上传图片并显示结果,服务器作为后端进行测量。
此测量方式跟传统测量方式(图2(b)[5])比较,有了很大改进。首先,它在测量时保持了沙堆的完整性,从而能够保证数据的可靠性,避免了传统测量方式只生成了半个沙堆而一定程度上破坏了沙堆的力学性质的缺憾。其次,传统测量方式进行测量时需要使用标尺,这个操作极易对沙堆造成破坏导致测量不准确。而拍照的方式能够最大程度地对被测对象进行保护。此外,在得到沙堆轮廓之后采用数学方法拟合直线计算角度,也要好于人的手工测量。因为沙堆的轮廓往往不是严格的直线,这使得手工测量极易因有主观性造成误差,而采用计算机数值计算的方法,可以消除这种主观性造成的影响。

图5 实验数据
通过此实验装置,我们实验得到了一系列沙堆含水量和休止角的关系,列在图5中,横坐标是含水量(水的质量与颗粒质量之比),变化范围从0到0.12,每变化0.01进行一组实验,纵坐标是休止角(大小用角度表示)。为得到充分的实验数据,同一含水量重复实验3次,由图显示,同一含水量下3次实验数据很相近,进一步验证了实验结果的可靠性。
2 理论分析
2.1 液桥力的计算
我们利用液桥力的相关理论,进一步理论分析沙堆休止角与含水量的关系。计算液桥力的前提是确立液桥模型(图6),并根据宏观含水量确定液桥含水体积。为简化模型,假设颗粒为直径相同的球体,根据含水量计算液桥体积如下:
(1)
式(1)中,ρp是颗粒密度;Rp是颗粒半径;nc°是配位数;ρ1是液体密度;ω0是含水量。

图6 颗粒液桥模型
液桥力是表面张力与静水压力之和
(2)
式(2)中,γ是填隙液体的表面张力;Δp液桥汽液界面压强差;rN是液桥颈部曲率半径。
为简化式(2)的计算,本文采取其回归形式.
计算式如下:
lnF*=f1°°-f2°exp(f3°lnS++f4°ln2S+)
(3)
2.2 修正系数的引入
《颗粒物质力学导论》[3]中使用液桥理论和水的表面张力理论,认为液体在颗粒间以小液柱(液桥)的形式存在,建立了含水量与颗粒间液桥力的大小关系,但是其公式中液桥与颗粒之间的接触角、液桥的距离都不能确定。因此公式使用起来有困难。
微小尺度上成千上万的颗粒、液桥相互作用最终决定宏观尺度上休止角大小,其物理过程需要的巨量计算在计算机技术发展后得以解决。Cundall P.A.等人发表文章提出了离散元方法(discrete element method, DEM),通过给定的相互作用力和边界条件,使用计算机蛮力迭代求解[4],这可以建立颗粒粘聚能量密度与休止角的关系,但是粘聚能量密度与液桥力之间的关系取决于目前无法确定的液桥与颗粒的接触面积。
在现有理论中,存在许多未知量,比如我们很难确定液桥距离S(参考文献[3]给出了液桥距离的计算公式,但实际距离与极限距离的关系难以确定),颗粒与液桥的接触角,以及在从液桥力向颗粒粘聚能量密度过渡时我们难以确定软球模型中颗粒的接触面积A。
诸多不确定因素使该公式无法计算出准确解,本文将不确定因素造成的影响集中起来引入修正系数修正。这些不确定因素都和含水量有关,因此修正系数应为含水量的函数设为δ(ω)。
EDEM是大型商用离散元仿真软件,它的原理是从某些在外力(如重力)条件下发生微小位移的离散元(如颗粒)开始计算,通过位移引发的受力变化计算其他颗粒发生的位移,不断迭代计算,直至所有的颗粒达到稳定状态,不再发生位移,就得到了受力平衡时的沙堆形状。
仿真时,需要控制的参数主要有4个:颗粒的形状、颗粒的半径、颗粒的密度以及粘聚能量密度。颗粒的形状、半径和密度应该与实验中实际使用的颗粒相近,所以颗粒形状近似为球形,平均半径取0.5mm,颗粒密度使用二氧化硅的密度2600kg/m3。而粘聚能量密度则是仿真的自变量,在其他3个参数确定不变的情况下,每指定一个粘聚能量密度,就进行一次仿真得到一个对应的休止角。仿真时的粘聚能量密度的范围是50000~140000J/m3,每隔10000J/m3做一次,一共得到了10组粘聚能量密度k和对应休止角θ的大小,发现有如式(4)的线性关系:
θ=0.0000793381k+35.356
(4)
为了确定修正系数的具体函数表达式,需要使用加入修正系数的公式和上述关系,使用实验数据进行最小二乘法拟合。发现修正系数的表达式采用如下形式效果最好。
(5)
式中参数如下:
p1=-51.01,p2=14.69,p3=-1.241,
p4=0.03918,p5=-0.0003692,
p6=6.177×10-7,q1=-0.09502,
q2=0.002622,q3=-6.745×10-5,
q4=3.11×10-6。
进一步,在理论模型下的拟合曲线如图7所示。至此我们找到了休止角与含水量的单值关系式。首先将含水量ω代入式(1)计算颗粒液桥体积,再将颗粒液桥体积代入式(3)计算系数F*,随后将系数F*与式(5)中的系数代入式(6)来计算黏聚能量密度,最后将黏聚能量密度代入式(4)即可得到休止角。
(6)

图7 引入δ的拟合曲线
2.2 休止角阶段性变化的性质描述

图8 休止角随含水量变化的四个阶段
由图8的拟合曲线,可以看到,当沙堆含水量在逐渐增大的时候,其休止角一直处于增大阶段,这说明沙堆在含水量较小时,随着含水量的增加,休止角依旧可以稳定增加,但当含水量达到一定区域约8%时,沙堆休止角就将随着其含水量迅速下降,此时沙堆的稳定性越来越差,直至坍塌。
进一步,我们分别对这4个阶段依次分析。
2.2.1 线性阶段
含水量在0%~4%左右,休止角-含水量曲线,近似为一条直线,休止角与含水量成正比,在该阶段过程中随着含水量的增加休止角也在增加,说明土壤的蓄水能力,没有达到饱和,还可以继续储水,在降水量较少时,土壤稳定性高。
2.2.2 水平阶段
含水量在4%~5%左右,休止角与含水量之间不再保持正比关系,当含水量增加的时候,休止角-含水量曲线出现水平线段,休止角不再随含水量的增加而增加。此时为休止角的稳定状态阶段,含水量微量变化时,休止角可以维持在一个固定的角度。
2.2.3 跃升阶段
含水量在5%~8%左右,先是含水量的小范围增加导致的休止角突变,之后随着含水量的增加休止角继续增加,且增长速度较快,该阶段沙堆依然保持一定的储水能力,但相比于近似线性阶段,储水能力下降,休止角随含水量的变化的反馈程度变得剧烈,8%为该阶段的极点,为非稳定的状态。土壤变得粘稠因而可以更稳定。
2.2.4 下降阶段
含水量大于8%,此时土壤的储水能力将遭到破坏,休止角随含水量的增加而减少,系统稳定性丧失,这表明降水量很大的时候土壤会从粘稠变滑,稳定性下降。
2.3 休止角阶段性变化的理论解释
由图9,可以看到修正系数大小变化的特征为,在不同的含水量区域修正系数随含水量的变化趋势不同,可以把含水量的区间分为0~4%,4%~5%,5%~9%,9%~12% 4个区间。

图9 随含水量递增导致的液桥变化
参考液桥变化图9[3],我们进一步给出理论解释。
2.3.1 线性阶段
含水量在0%~4%阶段,休止角与含水量成正比,该阶段颗粒间液桥通过接触点上的液桥发生黏连,该阶段含水量增加过程,导致休止角增加的原因可以理解为液体逐渐填隙在颗粒之间导致颗粒间的接触点数目增多,所以该阶段是线性阶段。
2.3.2 水平阶段
含水量在4%~5%阶段,接触点数目已经达到饱和,颗粒间液桥力的成型液桥形状基本不变,依旧可以等效为钟摆状,该阶段颗粒液桥达到该形状的最大容纳量。
2.3.3 跃升阶段
含水量在5%~8%阶段,此时液桥的形状正在由钟摆状转型为环索状和毛细管状,部分颗粒间隙充满液体黏连力增加。导致了休止角的突变和后续休止角的增加。
2.3.4 下降阶段
含水量大于8%,此时颗粒间有填隙液体,液体压力开始增加,液桥发生破坏,所以呈现微小的下降阶段。
3 结语
本文搭建了合理限制自由度的休止角生成装置,提出了以计算机视觉方式进行休止角测量的方法。进一步,通过引入有效修正系数理论,构建了休止角-含水量数学模型,并给出了与实验相吻合的物理解释。这有利于人们在已知含水量的情况下对休止角进行合理预测,对于泥石流预测等土力学应用问题,将具有重大意义。

