量纲方法与弹簧振子周期的二级质量修正
周国全 祁 宁
(武汉大学物理科学与技术学院,湖北 武汉 430072)
关于弹簧质量对谐振周期的影响, 其研究结论已散见于各种文献[1-4],一般是根据弹性理论建立振动微分方程加以解决。本文介绍一种简便而实用的方法——量纲方法[5-9],配合实验研究,可以在不求解弹簧谐振动系统的振动微分方程的情况下同样得出正确的谐振周期一、二级修正公式
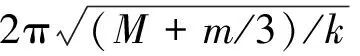
(1)
及
(2)
其中,M,m分别为弹簧振子及弹簧本身的质量;k为弹簧的劲度系数。通过这一实例,可以体会到量纲理论在物理教学研究中的辅助作用。
1 量纲和谐原理与Π定理的应用
量纲和谐原理要求:支配物理现象的数学物理方程的等号两侧的量纲表达式必须是相同的,亦即所涉及的各基本单位的量纲指数必须是独立而唯一的。这是量纲理论的基本要求。
具体研究思路如下:首先根据量纲和谐原理的要求,用量纲方法确定(M,m,k)振动系统周期T的基本形式,求出基本形式中各未知指数;寻找和构造若干独立的无量纲量,再根据Π定理,建立各无量纲量之间的函数关系,其中某些待定系数(或参量)可以通过理想情况或极限、特例情形的泰勒级数展开、精确的实验数据、巧妙的线性拟合技术加以确定。
以均匀直螺旋弹簧振子系统(M,m,k)为例,决定其周期T的因素如下:
① 弹簧劲度系数k;
② 振子质量M;
③ 弹簧的质量m。
量纲理论指出,周期T作为这一振动系统的一个特征物理量, 必然满足
T=CMαkβ
(3)
其中,α,β为待定常数指数;C是与一些无量纲量有关的因子。
设基本量纲为[L]=L,[T]=T;[M]=M;则[k]=牛顿/米=MT-2,量纲和谐原理要求[4,5]:等式(3)两侧的量纲表达式必须相同,故有
L0M0T1=Mα·(MT-2)β=L0Mα+β·T-2β
根据基本物理量(质量M与时间T)的量纲独立性,必有如下待定指数方程组

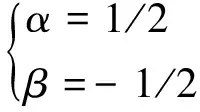
于是
(4)
作为范例之一,为了运用Π定理以分析这一振动过程的周期关于匀质弹簧质量的函数关系,我们要寻找和构造若干与问题相关的无量纲量。这在量纲分析理论中有一定程序化的手续[5-9],比较繁复。为了避免复杂的代数(如矩阵)运算,我们凭经验构造如下两个无量纲量。将有质量弹簧振子系统(M,m,k)的周期T与理想振子系统(M,0,k)的周期T0的公式
(5)
相比较,很明显我们可以构造一个有理化的独立的无量纲量μ
μ≡(T/T0)2
(6)
弹簧质量m与振子质量M之比,构成了另一独立的无量纲量ν
ν≡m/M
(7)
必须指出,我们凭观察和经验构造了两个无量纲量,当然可能遗漏其他独立的无量纲量,根据量纲分析方法中著名的Π定理,对于一个受到确定物理规律支配的、具有决定论性质的系统,这些无量纲量之间必定存在着某种确定的函数关系[5-9]:
Π(μ,ν,…)=0
(8a)
式(8a)等价于如下隐函数关系
μ=F(ν,…)
(8b)
相应于一个平稳连续的物理过程,除了物理状态的突变临界点之外,这个函数一定是光滑、连续而可微的。在此我们只关心无量纲参量μ随ν而变化的规律,在无量纲参量ν≪1,而其他无量纲量不变的情况下,我们对函数F(ν)在ν=0+附近作泰勒级数展开:
(9)
其中ci,(i=0,1,2,…,n,…),是待定常系数。
2 理想情形与周期修正公式

由此可得c0=1。当ν=m/M≪1时,仅保留式(9)中ν的一次方项,而略去ν的高阶无穷小项,可得
μ≐1+c1ν
(10)
代入式(6)、式(7),可得弹簧谐振周期的一级修正公式
(11)
这里c1为待定系数。式(11)表明,弹簧质量m对于谐振周期T的影响,即相当于以一定的折合质量c1m加入到振子质量M中去。在平面直角坐标系(μ,ν)中, 式(10)表示的μ与ν关系为一条斜率为c1,纵截距为1的射线(ν≥0)。当ν<1但不太小时,还可保留式(9)中的二次项,则有
μ=1+c1ν+c2ν2
(12)
代入式(6),式(7),可得弹簧谐振周期的二级修正公式
(13)
其中c1,c2也可通过精确的实验数据与巧妙的线性拟合技术求出。式(12)可化为
λ≡(μ-1)/ν=[(T/T0)2-1]/ν=c1+c2ν
(14)
其中λ与ν是一线性关系,c2为直线的斜率。
3 修正系数c1及c2的实验测定

实验结果表明:

值得提醒的是,实际上式(16)中的c2之值通过实验测量的误差很大,因为由c2带来的二阶修正值实际上已淹没在实验的偶然误差之下。姑且将它用如下理论修正值代替。基于弹簧的弹性理论, 建立起受载弹簧的振动的微分方程, 我们同样可求出弹簧质量对于振动周期的修正公式。理论上可导出[1]:
c1=1/3;c2=-1/9
(17)
于是弹簧谐振的周期的一级、二级修正公式分别为
这与我们用量纲方法及实验研究的结果正相吻合, 充分地证明了用量纲方法指导物理研究的方法论意义,其有效性与重要性毋庸低估。
4 结论
量纲方法之能有效地应用于科学研究,有其深刻的理论依据和厚实的实践基础。由于研究对象的结构多样性与运动复杂性,一些情况下我们无法建立严格有效的数理方程。所幸尽管存在困难,我们仍能借助量纲理论而得到一些富有启发意义的东西,在一些情形能够导出其物理规律的基本函数关系,在某些情形甚至能精确到仅差一个待定常数因子[9,11,12](如流体力学中的某些问题)。这给进一步的理论与实验研究提供了极有指导或参考意义的初始结论,正如前述范例所述。
量纲方法所得到的初步结论可以通过如下4种方法加以验证:(1)必须遵守量纲和谐原理,假定的函数方程的表达式中,各基本单位所要求满足的指数待定方程组必须是自治的。(2)用极限情形或理想情况下的已知结论去加以检验,或确定其中的某些参数。(3)用系统可能具有的对称性或周期性等特点去加以验证,或确定某些参数。(4)用实验结果加以直接检验,这是最根本、也是最终的检验方法。
总之,量纲理论与量纲方法不仅在科学研究中具有不可忽视的指导作用,而且在现代工程技术中也有重要的应用。工程上常用的相似模拟手段就直接来源于量纲理论,模拟的相似性判据更是量纲理论的直接结论。本文表明,量纲理论与量纲方法作为方法论的应用价值不容忽视。
——以匀加速直线运动公式为例

