静态双手拉车作业的肌肉疲劳分析与MET建模

唐范,易灿南,李开伟,2，左华丽,胡鸿,谢泽均

(1.湖南工学院 安全与环境工程学院，湖南 衡阳 421102；2.台湾中华大学 工业管理系，台湾 30012)

1 引言

在自动化水平大大提高的今天，人工搬运物料(Manual material handling,MMH)仍广泛存在于生产场所以及物流运输行业，通过手工完成提、拉、推、握等搬运动作[1]；而作业者长期不正确地进行手工搬运作业，容易产生肌肉疲劳，引起身体机能障碍，从而造成肌肉骨骼损伤(Musculoskeletal Disorders,MSDs)。在搬运方式中，拉、推是作业者更加倾向选择的搬运方式[2]；手动叉车由于能灵活地完成拉、推作业而被广泛应用。根据调查发现工人在工作时间内需多次使用手动叉车进行搬运作业[1，3]，而多次重复作业容易引起肌肉骨骼疾患[4]。利用手动叉车进行搬运作业时，通常可以使用单手或者双手来完成，在运载货物量过重的情况下，作业者更倾向于利用双手进行操作。易等[2,5-6]针对单手拉车作业的肌肉疲劳进行了研究，但针对双手拉车作业的肌肉疲劳研究还少有报道。

肌肉疲劳一直是工作设计研究中的重要课题，也是诱发MSDs的重要原因[7-8]。肌肉疲劳可以通过随着疲劳而产生的生理和心理症状来进行测量[9]，测量生理症状可以通过测量最大随意收缩(Maximum Voluntary Contractions,MVC)、最大耐受时间(Maximum Endurance Time,MET)和肌电图(Electromyogrphy，EMG)等来获得，心理症状的测量可以根据人员主观疲劳评分表(Ratings of Perceived Exertion,RPE)的评分来确定。从生理和心理两个方面着手观测肌肉疲劳，能够更加全面地了解疲劳发展过程，发现工作设计中是否可能存在工效学问题。

同时，一些学者基于肌肉疲劳的相关症状建立肌肉疲劳的预测模型，通过模型对肌肉和关节的疲劳以及变化进行预测[2,5,7-20]。在工效学中，预测模型一般分为两类：最大肌力随作业时间而变化的预测模型[2,8-10]和不同作业任务下可坚持的MET[5,7,11-20]。其中，MET模型输出结果为时间，非常适合确定静态作业的持续时间[21]，以及作息时间的安排[4]；因此，静态作业多以MET来构建预测模型。MET模型根据建模手段可以分为两种：针对特定关节或固定姿势下建立的实验模型[5,7,11-15,18-20]或基于力学分析而构建的理论模型[16-17]。现有静态作业MET实验模型[5,7,11-20]中的姿势与双手拉车实验中所采用姿势存在显著差异。Ma[16-17]基于肌肉疲劳的发展过程，建立了不受姿势和施力部位限制的MET预测理论模型，但是其模型中的疲劳速率K，计算时需假定其值等于1；实际上此值与作业任务相关，即不同作业任务下，K值存在差异，而目前无双手拉车实验K值大小的相关研究成果。因此，现有MET实验模型都不适合双手拉车作业，而理论模型是否适用，则需要进一步验证。

为了研究双手拉车作业的肌肉疲劳发展情况，本文通过模拟拉车试验测量被试的双手的MVC、MET、试验后双手的最大剩余拉力F，以及记录身体各部位的疲劳主观评价；探讨两种脚部姿势下MVC、MET、F以及疲劳评价值之间的关系，同时依据MET数据建立疲劳的预测模型，为设计拉车作业任务提供针对性依据，并评估MSDs 的风险。

2 对象与方法

2.1 被试

本试验共招募9名男性被试作为志愿者，所有被试身体健康均无肌骨骼的病历；实际作业中，拉杆与车身的夹角会随被试身高而改变，为控制由于被试身高不同而造成拉车角度改变的影响，被试的身高控制在160cm～170cm之间；所有被试要求在试验前24 h内无激烈运动。被试惯用手为右手，惯用脚为右脚，年龄21.11(±1.53)岁，身高163.85(±1.94)cm，体重60.33(±7.35)kg，身体质量指数22.79(±2.65)kg/m2，臂长为63.58(±2.33)cm，腿长为92.51(±2.54)cm，肩高为135.70(±2.08)cm，膝盖高为46.85(±3.99)cm。

2.2 试验设备

(1)拉力测量装置

由CHEMIST(FG-5100)肌力量测器、一条铁链、握杆以及连接在链中的S型单轴荷重传感器(loadcell)连结组成，用来测量被试的双手拉力。

(2)拉车模拟装置

基于实际测量手动叉车拉杆相关尺寸的基础上，设计模拟拉杆如图1所示，拉杆采用中空铝合金制作，拉杆总重1.5 kg，钢丝绳1和2固定在天花板上。实际拉车作业中，拉杆与车身的角度在36°左右，因此在试验过程中被试需维持拉杆与地面36°的拉车姿势，拉杆中间(即图1中40.5 cm处)悬挂50kg重物，经测量，被试维持拉车动作所需用力为170.03N。

(3)主观疲劳评价

采用RPE量表[22]，测量被试试验后身体各部位的疲劳或不适的主观感受。

2.3 试验方法

(1)试验准备阶段，试验员指导被试熟悉试验装置的操作，说明注意事项，确保被试完全熟悉后开始试验。本研究的预试验显示被试的肌力于无暖身运动下有较高的变异，适当的暖身运动有利于被试肌力的呈现，并减少数据的变异，同时也能避免肌肉拉伤。因此试验前10 min被试跟随视频进行5 min肌肉拉伸运动，以达暖身效果。

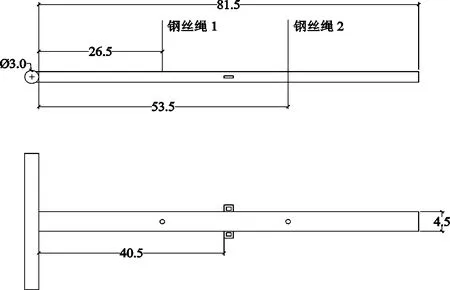
图1 模拟拉杆尺寸

(2)拉力测量阶段，暖身运动休息5 min后，测量其双臂的拉引肌力，测量过程中，被试面向测量装置，双手紧握车柄，身体向后倾斜，左右脚一前一后间距40 cm蹬地来完成动作，过程中需要保持前脚直立、后脚弯曲，双手握持握柄并以最大意志施力向链条方向拉引，持续施力约4 s至6 s，此时显示器上显示的力值即为被试在该姿势与条件下双手的MVC。

图2 模拟双手拉叉车试验

(3)拉车模拟阶段，被试测量最大拉力值后，休息3 min后进行模拟拉车试验。被试到指定位置后，保持与测量拉力时一致的动作拉引模拟装置，如图2所示，被试要求保持姿势不变，持续施力直至感觉身体无法承受时，即告知试验员；试验员立即接过拉杆停止试验。试验结束后，被试进行F的测量，其测量过程与MVC测量过程一致；同时，要求被试告知感觉身体无法承受时，其身体各部位的疲劳或不适的感受的RPE主观评分。

静态双手拉车作业根据脚部姿势可以分成左脚前立和右脚前立两种状态。被试需完成右脚前立和左脚前立的试验，每种情况进行两次重复试验，即被试需完成4次试验，试验顺序随机安排，且每两次试验需间隔24 h以上。

3 结果

3.1 疲劳分析

运用统计软件SAS®9.0进行方差分析(Analysis of Variance，ANOVA)，通过拉车试验，被试双手的拉力均显著下降(P<0.0001)，试验前双手拉力(MVC)为300.53(±29.68)N，试验后拉力(F)为234.40(±29.68)N，平均下降21.67(±7.53)%；分析结果显示，脚部姿势对MVC、F和拉力下降均没有显著性影响。CORR分析表明BMI与MVC的Pearson相关系数为0.61(P<0.0001)，BMI越高者其MVC越大。

对RPE进行ANOVA分析可知，同一脚部姿势下，前立脚的下肢部分(脚掌、小腿、膝盖)与后立脚相应部位的RPE存在显著差异(P<0.0001)，而左右上肢部分(手部、肘部、肩部)的RPE没有产生显著性差异；两种脚部姿势的上肢部分(手部、肘部、肩部)和腰部的RPE没有显著差异；试验中前立脚掌的RPE是显著高于其他部位的RPE(P<0.0001)，同时也显著高于后立脚掌的RPE(P<0.0001)；上肢部分的手部RPE也显著高于上肢的其他部位(P<0.0001)，如表1所示。

静态双手拉车作业的MET值为9.87(±2.39)min，ANOVA分析结果显示脚部姿势对MET没有显著影响。现有研究结果表明，负荷强度fmvc(fmvc=外部负荷/MVC)是影响肌肉疲劳的重要因素[23]。双手拉车条件下，fmvc范围为0.47～ 0.78，平均值为0.57(±0.06)。CORR分析结果表明，fmvc与MET显著负相关(P<0.05)，Pearson相关系数为-0.32。

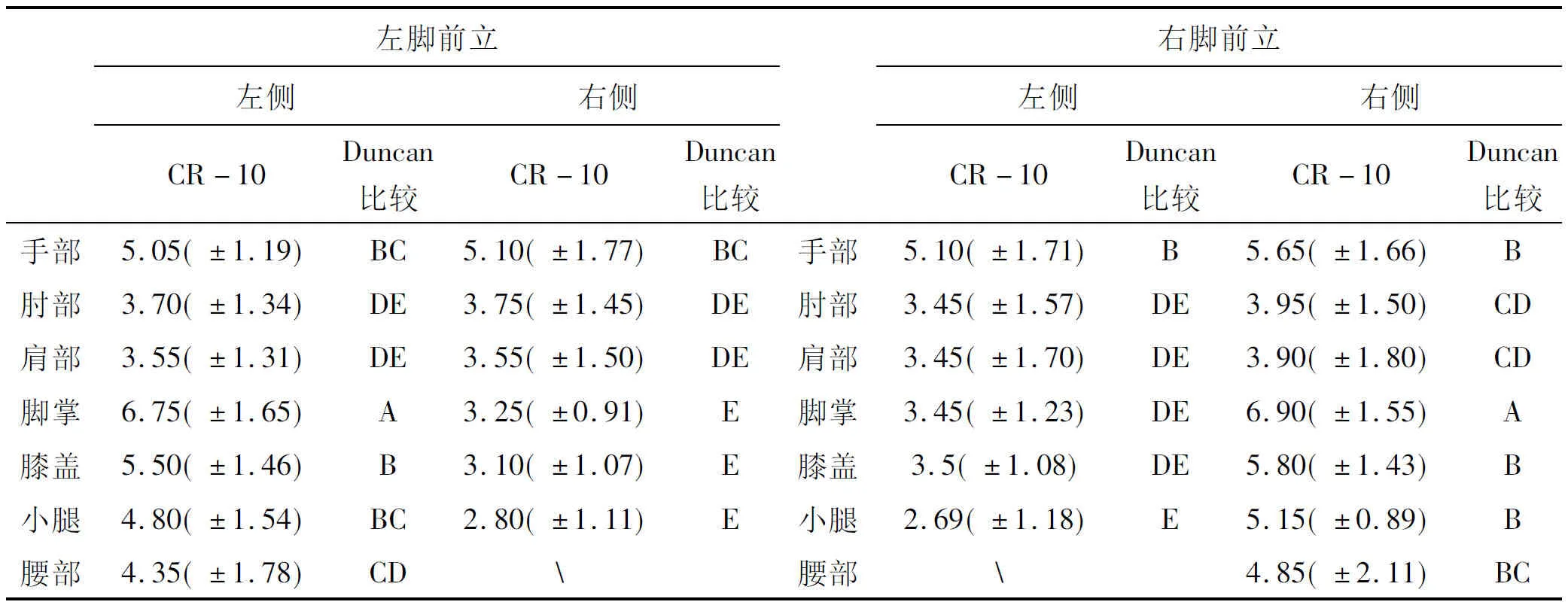
表1 不同脚部姿势下主观疲劳值ANOVA分析结果

3.2 MET建模

MET模型一般是以fmvc来构建预测函数，多以指数函数、幂函数形式来构建MET模型[5,7,13-14]，部分MET模型是以多项式、倒数等形式构建[15,18-20]。本文以指数函数、幂函数和对数函数建立MET模型，可以假设模型为：

MET=k×exp(cfmvc)

(1)

(2)

MET=k+c×ln(fmvc)

(3)

其中k为疲劳速率，min-1；c为常数。

式(1)、(2)可以转换为：

lnMET=lnk+c×fmvc

(4)

lnMET=lnk+c×ln(fmvc)

(5)

将试验数据转换成式(3)、(4)、(5)的变量的形式，通过线性回归分析，可得MET的回归方程如表2所示：

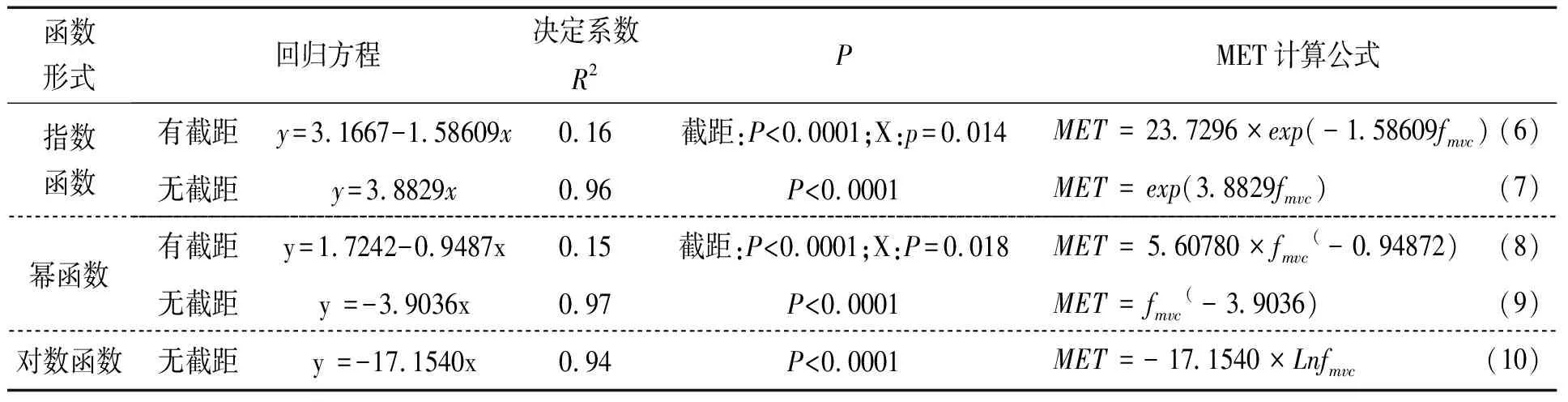
表2 双手拉车作业MET回归方程

根据表2可知，式(7)为升函数，不符合3.1节中提出的MET与fmvc为负相关关系的要求；式(6)和(8)的决定系数均小于0.5(R2<0.5)，自变量 fmvc对因变量MET的解释程度低；式(9)和(10)的决定系数均大于0.9(R2>0.9)，自变量fmvc对因变量MET的解释程度高；因此确定式(9)和(10)为静态双手拉车的MET预测模型。

平均绝对偏差(MAD)和相对偏差(PMAD)可以比较MET实测值与预测值之间的差距，其计算公式见式(11)和(12)：

(11)

(12)

式(9)、(10)的MAD和PMAD见表3。为进一步为验证所建预测模型的合理性，将双手静态拉车试验数据代入现有MET方程，分析MET- fmvc并计算其偏差。根据静态拉力作业的特点以及RPE结果，选取易等提出的单手拉车作业模型[5]、Ma的疲劳模型[16～17]、一般模型[14～15]、手部模型[13～14]以及腰/背模型[14,7]进行对比分析，获得MET- fmvc曲线图(图3)和各模型下的MAD和PMAD(表3)。图3显示本文所建模型与现有模型具有相同下降趋势。由表3可知：本文所建模型的偏差最小，其次是单手拉车作业模型(MAD>5.1,PMAD>49%)，腰/背部模型的偏差较大(MAD>7.2,PMAD>72%)，而Ma提出的疲劳模型、一般模型以及手部/抓握模型的偏差均比较大(MAD>8.5,PMAD>86%)。因此，本文所建的模型更适合反映双手拉车作业过程中肌肉疲劳发展的情况。

表3 本文建立预测模型与部分现有MET模型的MAD和RD

注：Ma的疲劳模型中的K=1。

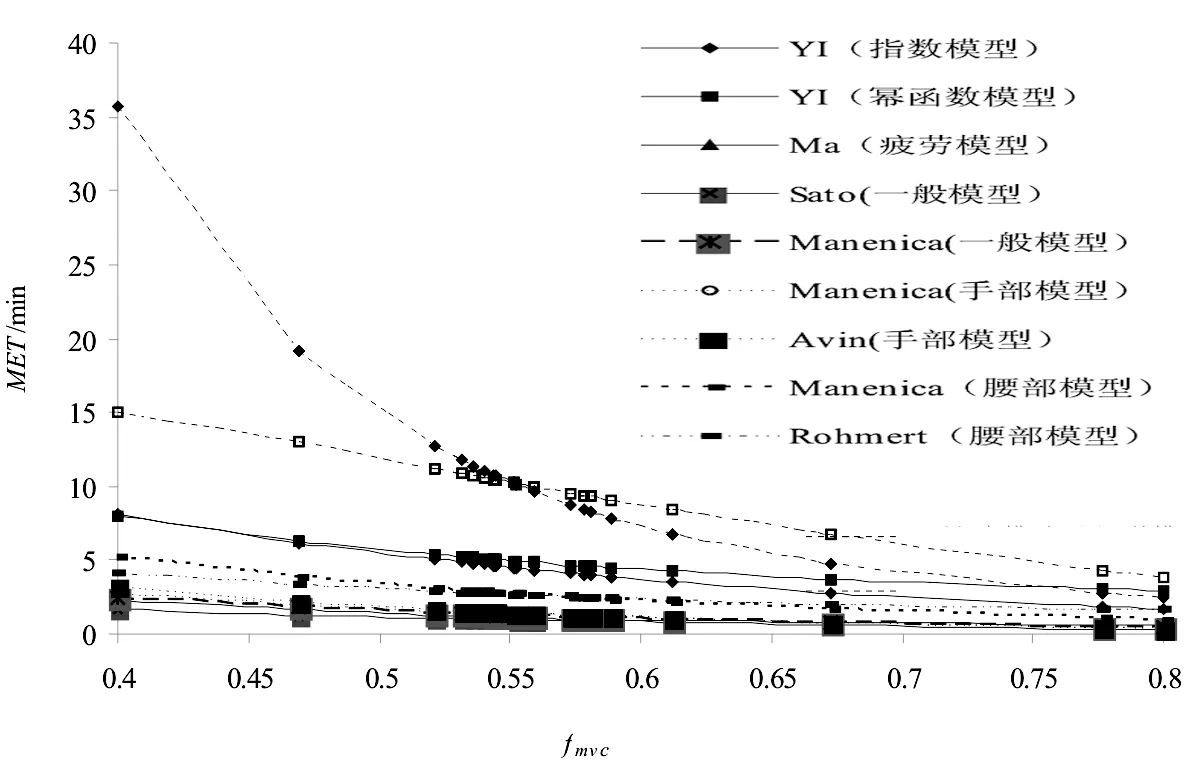
图3 MET 模型的 MET-fmvc 曲线图

4 讨论

本研究通过模拟静态双手拉车试验，设计两种脚部姿势，来对双手拉车状态下肌肉疲劳的发展情况进行了探讨，并根据MET建立双手拉车作业的肌肉疲劳预测模型。模拟试验的负荷设置为50 kg，被试在该负荷下需要用170.03N的拉力来维持模拟叉车的静止状态。负荷强度fmvc范围为0.47～0.78，平均强度为0.57(±0.06)，该负荷强度是大部分作业者长期承受的强度[5]。

脚部姿势对MVC、F、MET均没有产生显著影响，可能是由于模拟拉车作业中，被试通过拉力来保持重物静止状态，拉力主要是通过上肢和躯干部位施力来完成，而脚部在作业过程中主要起到保持上半身平衡的作用，与拉车的拉力没有直接作用关系。根据主观评分值分析发现，脚步姿势对上肢部位和腰部的RPE也没有产生显著差异，也进一步说明上肢和腰部的疲劳产生与脚部姿势无关。

试验中前立脚掌的RPE是显著高于其他部位的RPE(P<0.0001)，同时前立脚掌的RPE显著高于后立脚掌(P<0.0001)；在试验中，被试持续保持拉叉车的静止动作，直至感觉身体承受不住即停止试验，而从主观评分的结果来看，前立脚掌的疲劳感是决定被试停止试验的关键。在同一脚部姿势下，左侧的手部、肘部和肩部与右侧相应部位的RPE不存在显著性差异；CORR分析结果显示，左右两侧上肢对应部位的RPE相关程度非常高，左右两侧手部、肘部和肩部的相关系数分别为0.82(P<0.0001)、0.84(P<0.0001)、0.83(P<0.0001)。

通过MET模型的MAD和PMAD比较(表3)分析可知，本文所建MET模型偏差最小(幂函数：MAD=2.72±2.18min、PMAD=27.49±19.47%；对数形式：MAD=1.92±1.58min、PMAD=19.85±15.11%)。单手拉车作业模型[5](指数模型、幂函数模型)的偏差相对较小，MAD分别为(5.61±2.28)min和(5.10±2.275)min，PMAD分别为(55.14±11.42)%和(49.36±11.62)%；这可能是由于两试验条件的相似性，同为拉车模拟试验；但双手与单手拉车作业在拉车姿势、施力方式等存在的差异，也使得偏差大于5min。由上文分析可知，拉力主要由上肢和躯干部位施力来完成，脚部主要起保持上半身平衡的作用；而在上肢和躯干部分的RPE中，手部和腰部的RPE最高，是被试感知疲劳最为明显的两个部位，因此，本文选择了手部模型和腰/背部模型进行对比分析，但分析结果显示，手部模型[14-15](MAD>8.5,PMAD>86%)和腰/背部模型[14,7](MAD>7.2,PMAD>72%)的偏差都比较高；这可能是由于试验过程中，被试的手部除了产生拉力以外，还需依靠手部进行抓握拉车手柄，持续的抓握动作导致手部充血和麻木，从而导致被试对手部疲劳感知增强；同样，腰部在试验过程中不仅起到施力的作用，还需起到保持姿势(拉车过程中要求被试稍微向后倾斜)的作用，从而使其疲劳感增强。一般模型[14-15](MAD>8.5,PMAD>85%)的偏差比较大，可能是由于试验所测姿势、负荷水平和施力方式不同所导致。

Ma[16-17]的疲劳模型中建议集体疲劳速率K设定为1，但当K=1时，疲劳模型计算的结果比实际值存在8.8 min的偏差(MAD>8.8,PMAD>89%)；易等[2]研究表明K值是由作业任务决定，因此将双手拉车的试验数据MET和fmvc进行计算，可知双手拉车的疲劳速率K=0.11(P<0.0001)，此时疲劳模型计算的结果比实际值只存在2.16 min的偏差(MAD>2.1,PMAD>22%)，与本文所建模型的偏差水平比较接近。

值得指出的是，双手拉车作业在实际作业中是动态的作业过程，作业者的行走速度、行走姿势、用力习惯以及作业者长期作业的累积疲劳等都会影响肌肉疲劳；不同水平的负荷也会对肌肉疲劳产生不同影响，但在本研究中，由于条件的限制，只考虑了静止状态下50kg负荷水平的双手拉车试验；后续可研究更多水平的负荷以及动态作业的肌肉疲劳情形，进一步完善和修正MET模型。

5 结论

(1)双手拉车作业使被试的拉力显著下降，拉力的大小与被试的BMI存在正相关关系；脚部姿势对MVC、F、MET没有显著影响，对上肢和腰部的RPE也没有显著影响，对下肢的RPE存在显著影响；在同一姿势下，前立脚的脚掌、小腿和膝盖疲劳感明显强于后立脚，前立脚掌的疲劳感是决定停止拉车试验的关键。

(2)建立的幂函数和对数函数形式的MET预测模型，其预测值与实测值之间偏差均较小，可运用该预测方程对双手拉车作业者在作业过程中的肌肉疲劳进行预测。同时，修正Ma的预测模型中的疲劳速率，修正后的疲劳模型能反映双手拉车的肌肉疲劳发展过程。

(3)由于条件所限，试验设计为静态的拉车作业，但在实际拉车作业是一个动态作业过程，双脚交替移动，在后续研究中，可以将动态的因素考虑进来。此外，试验中负荷只有50kg一种水平，这与实际作业中负荷水平多的情况不符，未来研究可讨论更广泛的试验负荷条件。