超大型集装箱船支撑舱壁过渡结构疲劳强度研究

陈星达，郁惠民，谢永和，王 伟

(浙江海洋大学船舶与机电工程学院浙江舟山 316022)

相对于传统的干散货船、杂货船而言，以标准运输单位进行海上运输的集装箱船，其运输具有更便利、更有效率、更安全的特点，因此，传统意义上的干散货船逐渐被集装箱船取代，成了海上运输的主力军。

对于集装箱船的横舱壁，可以把该区域可分为上部及下部。在上部区域，与纵舱壁连接的结构大部分都为箱形抗扭箱结构，横舱壁的水平平台在与纵舱壁连接处通常设有肘板，该处结构的应力变化范围比较大，这是由于受到船体总纵弯曲以及扭转应力的作用。为了缓解这种情况，建造过程中一般会采用软趾结构、大型肘板或者两者结合的过渡结构，以此来减小交汇处的折角大小，提高该处的抗疲劳性能。不过，对于过渡结构处疲劳强度的研究尚且欠缺，相关文献也难以查阅，导致在集装箱船设计与建造过程中如何选取合适的过渡结构形式成为一个难题。

本文从疲劳强度出发，试图通过改变该过渡结构处的不同连接形式，并对其进行疲劳强度的计算，对比不同结构形式下的疲劳寿命，以此来寻求一种相对较好的大型集装箱船支撑式横舱壁过渡结构形式。

1 疲劳简化分析法

本文主要采用疲劳分析法的简化分析法，选择货舱区域关键位置的船体结构节点进行疲劳强度评估。疲劳简化分析法的主要步骤有：疲劳载荷计算、载荷工况设定、热点应力范围计算、选择S-N 曲线、累积损伤度的计算及衡准。

此外，对于设计的疲劳寿命，总累积损伤度D 在此期间内应满足式(1)要求：

其中：TD/a 为设计疲劳寿命，对于集装箱船的设计疲劳寿命一般为20 a。

2 疲劳强度计算

2.1 疲劳累积损伤计算

结构节点均匀满载“k1”与正常压载“k2”两种装载工况中的累积损伤度Dk应按式(2)计算：

式中：ND为集装箱船在设计疲劳寿命规定的年营运期间内载荷循环的总次数，取0.65×108；NL为载荷谱回复周期的循环次数，取为102；∂k为均匀满载“k1”与正常压载“k2”两种装载工况中的时间分配系数，对于集装箱船，均匀满载状态下的各子工况取为0.65，正常压载状态下的各子工况取为0.2；K 为S-N 曲线参数，如表1；SD(k)为均匀满载“k1”与正常压载“k2”两种装载工况的设计应力范围，N·mm-2；ζk为均匀满载“k1”与正常压载“k2”两种装载工况中的Weibull 形状参数，取为1；

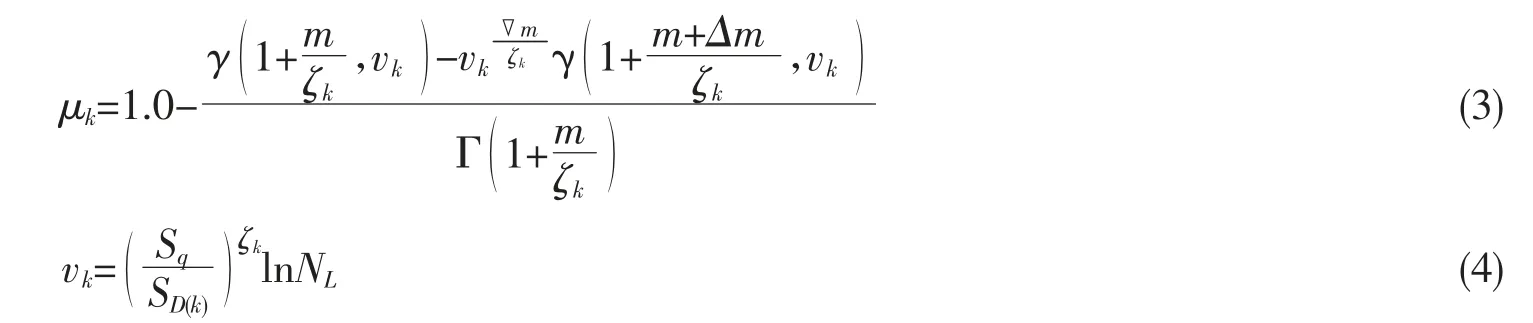
其中：m 为S-N 曲线反斜率，取为3；Δm为S-N 曲线两段反斜率差，取为2；γ（x,v）为不完全GAMMA函数，按式(5)计算：

Γ 为完全GAMMA 函数值，应按式(6)计算：Sq为S-N 曲线在交汇处的应力幅值，如表1。

表1 S-N 曲线参数Tab.1 S-N curve parameters

结构节点的总累积损伤度按式(7)计算：

式中：Dk为结构节点在均匀满载“k1”与正常压载“k2”两种装载工况下的累积损伤度。

结构疲劳寿命应按式(8)计算：

式中：D 为结构节点的总累积损伤度，见式(7)。

2.2 设计应力范围

均匀满载“k1”与正常压载“k2”两种装载工况中的设计应力范围SD(k)应按式(9)计算：

式中：Sh,i(k)为均匀满载“k1”与正常压载“k2”两种装载工况中编号为“i”的载荷工况下的热点应力范围，N·mm-2；fm，i(k)为均匀满载“k1”与正常压载“k2”两种装载工况中编号为“i”的载荷工况下的热点平均应力修正系数；ft为板厚修正系数。

3 实船计算

3.1 超大型集装箱船基本数据

本文以某12 200 TEU 集装箱船为例，其主尺度为：总长327.61 m，垂线间长313.13 m，设计船长309.15 m，型宽48.20 m，型深27.20 m，设计吃水13.00 m，结构吃水15.50 m，航速22 kn，方形系数0.678 9。

3.2 有限元模型

本文所分析的有限元模型选取了靠近船中位置处的舱段，包括了66-87 肋位之间的一整个货舱以及前后延伸的半个货舱，总长度为2 个货舱舱段结构。建模的过程主严格按照有限元建模原则进行，利用MSC.Patran 建立有限元模型如图1，分别为集装箱船的全宽模型和半宽模型。

图1 12 200 集装箱船舱段全宽模型Fig.1 Full width model of 12 200 container cabin section

3.3 计算工况

用于本文疲劳强度计算的工况称为计算工况，由各疲劳评估的两种装载工况，即正常压载和均匀满载，与及其对应的载荷工况组合而成。对于每一个疲劳评估装载工况，应考虑用于疲劳评估的动载荷组合之后所形成的所有疲劳载荷工况。对于每一疲劳评估装载工况的主导载荷工况选取，需要计算在热点处的所有载荷工况下的设计应力范围，选取其中热点应力范围值最大的载荷工况作为该装载工况下的主导载荷工况。

对于两种典型的装载工况，即均匀满载和正常压载，其12 种载荷工况将由以下规则波组成：

1)H：指在迎浪状态下，其垂向波浪弯矩达到最大时的一种规则波；

2)F：指在随浪状态下，其垂向波浪弯矩达到最大时的一种规则波；

3)R：指船舶在横摇运动达到最大时的一种规则波；

4)P：指船舶在水线处水动压力达到最大时的一种规则波。

将等效设计波与12 种载荷工况相对应，可得到如下12 种载荷工况：

H1、H2、F1、F2、R1P、R2P、R1S、R2S、P1P、P2P、P1S、P2S

3.4 过渡结构形式

在集装箱船的支撑式横舱壁位置，需要在内舷侧与上部抗扭箱相交处建立过渡结构，使其能够满足结构强度以及疲劳强度。因此，本章针对一般形式的过渡结构，及仅有大肘板作为支撑的过渡结构形式展开讨论，并设计了另外几种有关延伸结构与大肘板组合的过渡结构形式，并将几种过渡结构进行系统的对比，分析其疲劳强度与疲劳寿命，并讨论各个结构形式之间的差异与优劣。

设计的3 种支撑式横舱壁过渡结构形式如图2～4：

图2 形式一Fig.2 Form one

图3 形式二Fig.3 Form two

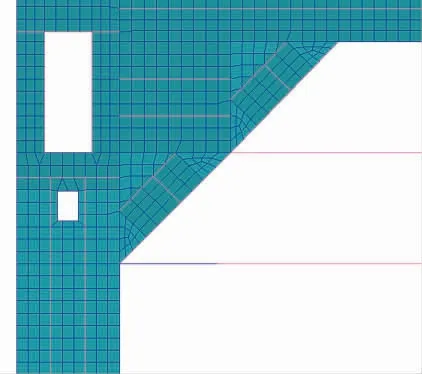
图4 形式三Fig.4 Form three

对于支撑舱壁处的第一种过渡结构形式选取，主要是考虑将其用于无一般大肘板情况时，过渡结构处疲劳强度与疲劳寿命的对比，因此设计了一种既无延伸结构，也无大肘板作为支撑的过渡结构。支撑舱壁的第二种结构形式，既安装了大肘板作为支撑，也做了棱角处的结构延伸。此外，支撑舱壁结构形式三为过渡结构处有大肘板作为支撑，但没有延伸结构。

3.5 疲劳评估热点位置

针对集装箱船支撑式横舱壁处的过渡结构，选取了内舷侧板与上层抗扭箱交汇处周围的节点为疲劳评估的热点，根据以上3 种不同形式的过渡结构，共有节点5 个。此外，为更好地对集装箱船进行疲劳评估，还对一个集装箱船的常规疲劳评估位置进行了疲劳计算，即位于1/4 舱段位置的内底板与内舷侧相交处节点。因此，表2 主要进行了6 个热点的疲劳计算。各热点的具体信息如表2。

在计算疲劳寿命时，为了能让应力呈现梯度的变化，需要将每一个热点处的有限元网格细化为比较小的精细网格，具体的大小尺寸一般可以取为与该处的板厚厚度一致。因此，在确定了各个疲劳热点的位置之后，对于现有的有限元粗网格，各个热点处的模型细化工作需按照有限元建模原则进行。图5～10 为各疲劳热点细化后的有限元模型图。

图5 HotSpot1 的有限元细化模型图Fig.5 Finite element refinement model diagram of HotSpot1

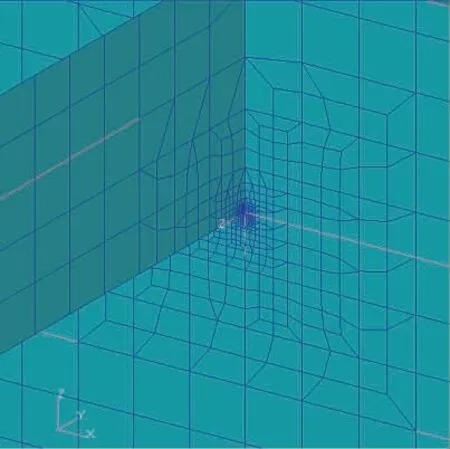
图6 HotSpot2 的有限元细化模型图Fig.6 Finite element refinement model diagram of HotSpot2

图7 HotSpot3 的有限元细化模型图Fig.7 Finite element refinement model diagram of HotSpot3

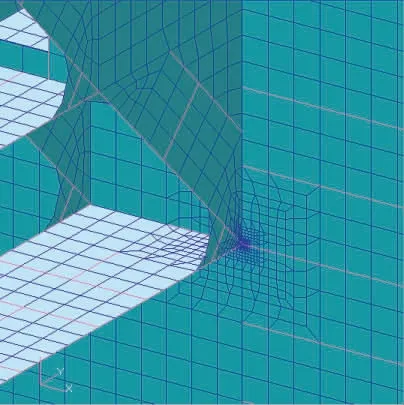
图8 HotSpot4 的有限元细化模型图Fig.8 Finite element refinement model diagram of HotSpot4

图9 HotSpot5 的有限元细化模型图Fig.9 Finite element refinement model diagram of HotSpot5

图10 HotSpot6 的有限元细化模型图Fig.10 Finite element refinement model diagram of HotSpot6

3.6 疲劳强度计算结果

在得到各位置处热点的热点应力范围后，可以乘以相应系数进行设计应力范围的计算，并选取设计应力范围最大的载荷工况为主导载荷工况，选取相对应的合适的S-N 曲线，并根据2.2 节疲劳损伤度计算公式，得到了集装箱船支撑式横舱壁过渡结构处各热点的疲劳损伤度和疲劳寿命，如表3。

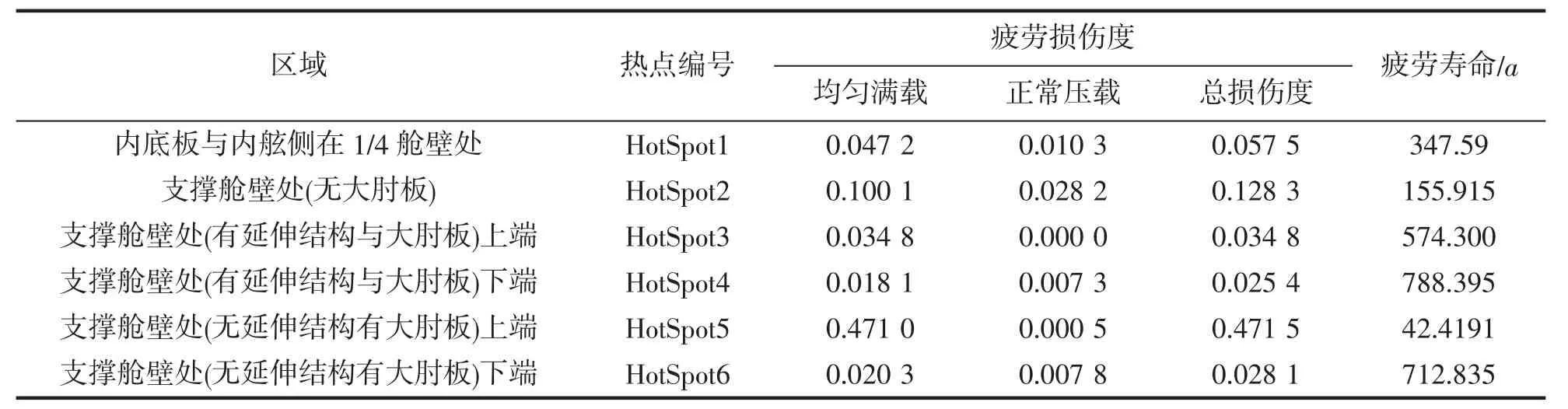
表3 各热点疲劳损伤度与疲劳寿命Tab.3 Fatigue damage degree and fatigue life of each hot spot

4 结论

围绕超大型集装箱船存在的疲劳强度问题，本文针对12 200 TEU 集装箱船的支撑式横舱壁的3 种不同形式的过渡结构进行了计算，并比较它们之间的差异。计算结果表明，本文选取的3 种过渡结构形式中各热点疲劳寿命均满足规定的20 a 标准。另外在综合考虑结构强度，疲劳寿命，以及结构轻量化的前提下，得到了一种最为合适的过渡结构形式。该结构有大肘板，且在靠近上部抗扭箱位置安装有延伸结构，在靠近内舷侧位置无延伸结构。