CIPSO算法在城市有轨电车控制策略中的应用研究

罗 淼,米根锁

(兰州交通大学自动化与电气工程学院,兰州 730070)

在保证电车安全运行的前提下，对电车运行过程采取不同的控制策略会使电车的能耗减少，提高电车的正点率，电车停靠站台时的精准度，降低电车运行的能耗同时提高运行过程中乘客的舒适度。文献[1]中对电车的运行过程进行了分析，主要分为启动、恒定加速、匀速、调速运行和制动停车，并采用了模糊神经网络方法对电车的运行过程进行优化，获得了高速列车运行的控制策略，但模糊神经网络本身存在一些固有的缺陷，优化过程中易陷入局部最优，实时学习和泛化能力较差，学习收敛速度较慢；文献[2]通过混合微粒群算法优化了多目标的高速铁路列车的控制策略，但文献中所采用的工况序列固定，具有一定局限性，且混合PSO(Particle Swarm Optimization，微粒群优化)算法计算量大，实时性差；文献[3]采用速度变异的粒子群算法提高了列车运行的能源利用率，但只对列车的运行能耗进行了优化；文献[5]基于混合系统模型预测控制HMPC的列车自动驾驶策略，合理的分配动车组各车厢的牵引力和制动力，节约了能耗，保证了动车的正点率，由于只采用了局部线路数据进行优化，获得的结果全局性较差，更适合对于传统的PID控制策略进行优化；文献[6]采用粒子群算法通过挖掘线路信息和列车运行信息指导优化过程，获得满足一定能耗、运行时间误差和停站误差的全局ATO控制策略，优化目标中未加入对乘客舒适度的考虑。综上可以看出，目前大多都是针对高速铁路列车的运行控制策略问题进行优化，且优化目标考虑不够全面，对于城市有轨电车的控制策略优化几乎处于空白。

结合我国轨道交通的运营特点，以城市有轨电车为研究对象，对电车运行过程中正点率、乘客舒适度、停靠准确性以及能耗为优化目标，以电车安全因素与动力学方程为约束条件，建立城市有轨电车运行过程多目标优化模型。采用混沌映射、免疫接种和免疫选择对PSO算法进行改进，利用改进的算法，对建立的电车运行过程多目标优化模型求解，得到最优的电车控制策略。

1 电车运行过程多目标建模

在城市轨道交通运行环境中的电车运动方程为[7-8]

(1)

式中，s表示电车在线路上位置，s∈[0，S]，S为区段全长；t表示电车运行时间，v表示电车运行速度，t∈[0，T]，T为给定的电车全程运行时间；v∈[0，V]，V为所允许的电车最高运行速度；u表示为输入控制序列包括制动“-1”、惰行“0”、牵引“1”，u∈{-1，0，1}=U。根据电车牵引特性曲线确定牵引力f(u，v)，牵引力与电车运行过程中的输入控制序列和电车的运行速度有关；电车附加阻力ω(s，v)，主要由电车的实时位置信息和速度求解；制动力b(u，v)，主要由电车运行时的控制策略，电车实时速度以及车辆制动性能求解。电车的3种运行状态可以定义为

(2)

电车运行过程中主要以4个方面为目标建立城市有轨电车运行过程多目标优化模型[9-12]。

目标1：令电车早晚点指标F1最小，此时电车正点运行的概率最高。电车在区间运行的总时长为T′[13]

(3)

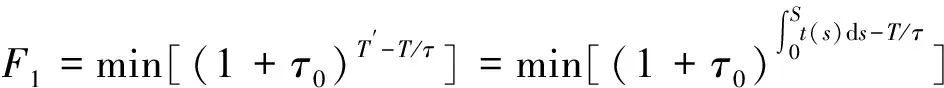
(4)

式(4)中，τ为电车容许早晚点的时间长度；τ0为电车在容许范围内晚点后，让电车调整至正点到达时间所需要的单位能耗，为惩罚项系数；F1指标反映了电车运行时正点到达的情况。综上在容许早晚点时间长度内时，F1取值较小，若电车晚点时间大于容许早晚点时间长度，F1的取值会快速增大。

目标2：乘客不舒适度最低，不舒适度指标F2，通过冲击率对整个运行时间的积分来获得[3-4]。

(5)

目标3：令电车运行全程所走行的实际距离与线路全长的差距F3最小，此时电车在车站内停靠站台的位置准确性高。电车进站后的实际停靠站台点位置为

(6)

F3=min[(1+σ)|S′-S|/S0]

(7)

其中，σ为惩罚项系数；S0为容许停靠站台的位置误差，根据具体情况确定。电车进站停靠站台后在线路上停靠点距预计停车点越近，F3越小，反之越大。

目标4：电车能耗最小。根据所有的(t，v)∈[0，T]×[0，V]，u∈U，电车不同输入控制序列在线路[0，S]上对应的能耗F4最小[14-15]。

(8)

本文利用加权和的方法将多目标优化问题转化为单目标优化问题，并采用CIPSO算法在优化过程中容易实现，精度高，收敛速度快等优点，以城市轨道交通运行环境中的有轨电车为研究对象，对电车运行过程中的多个目标求解，得到最优控制策略，其目标函数为

F=min[λ1F1+λ2F2+λ3F3+λ4F4]

(9)

因此电车运行控制策略的多目标优化模型为

(10)

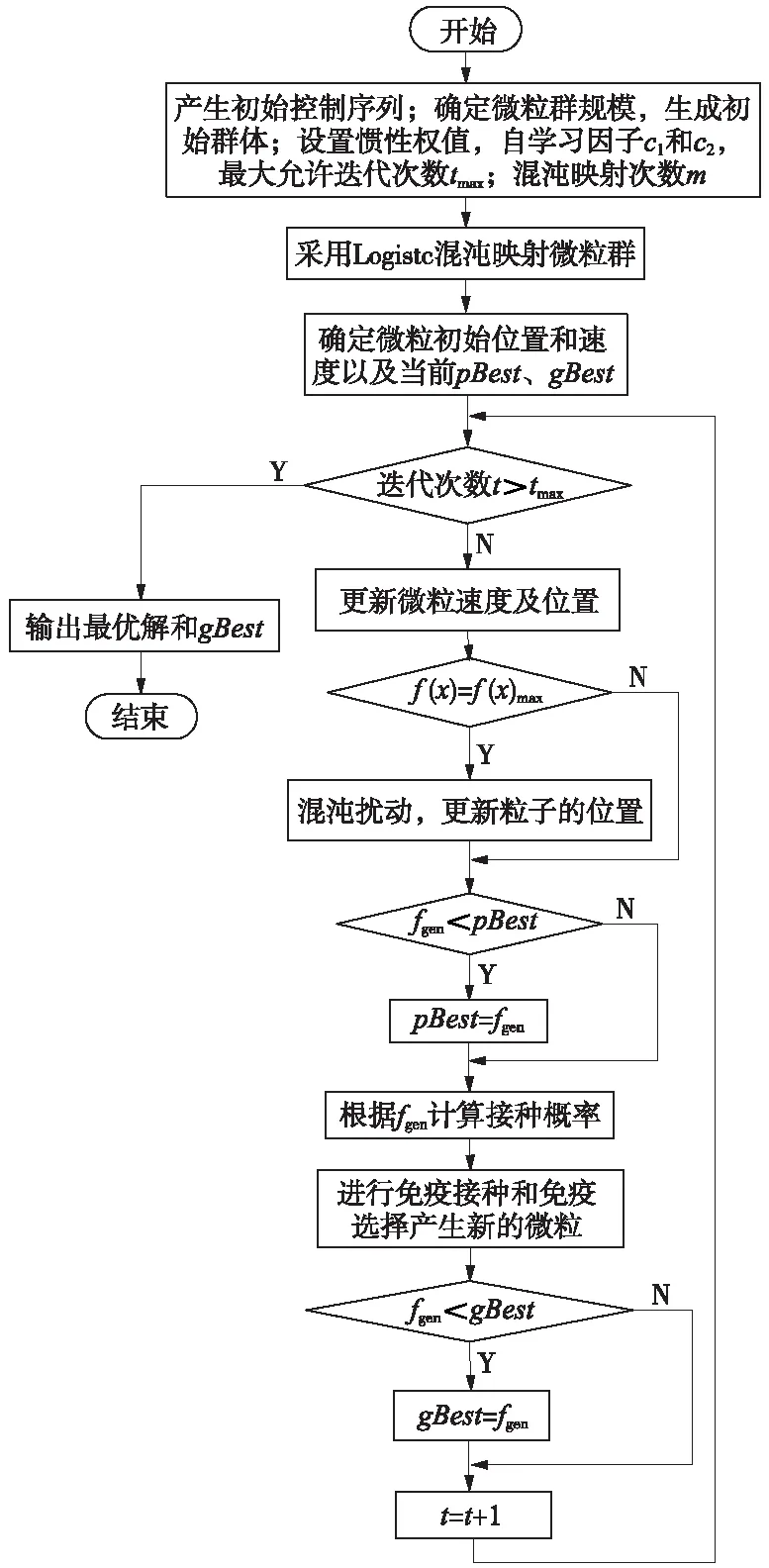
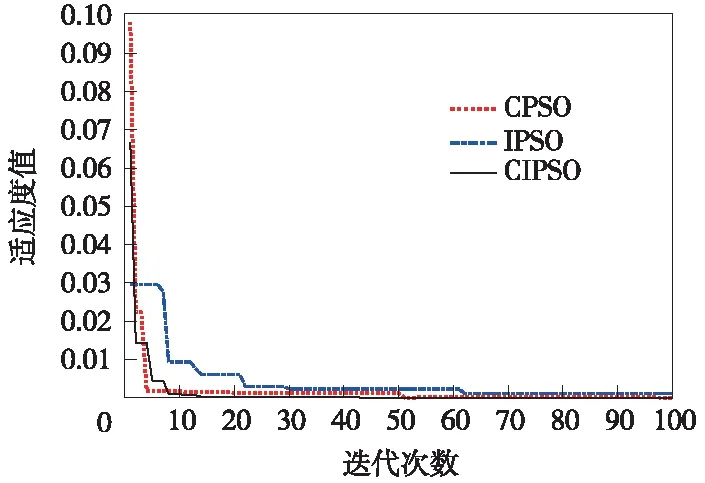
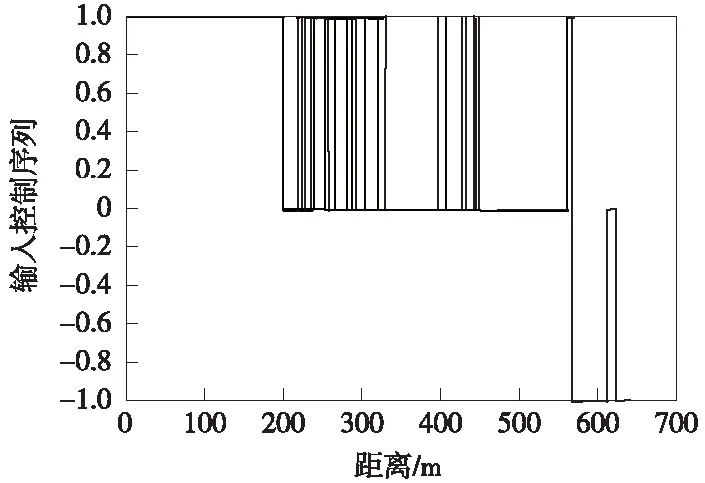
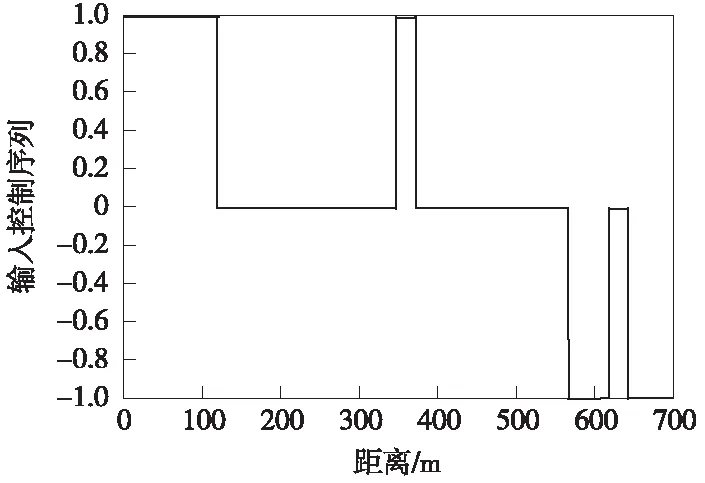
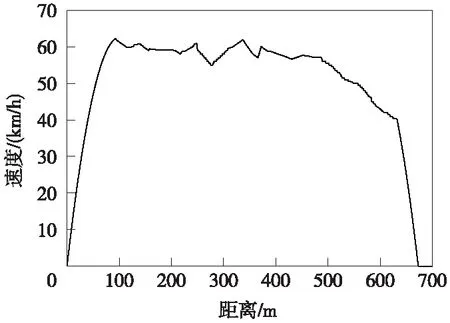
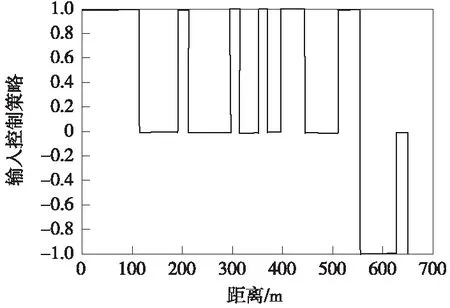
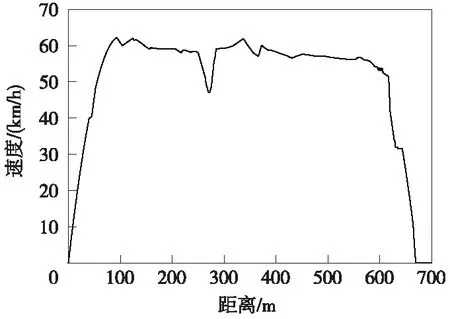
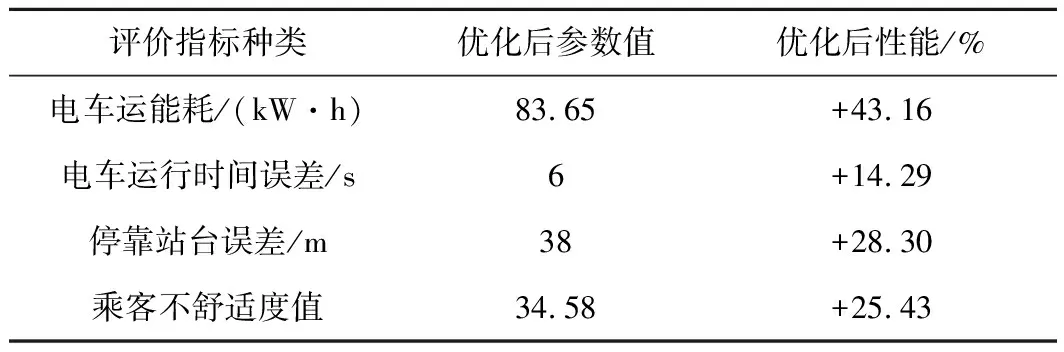
式(10)中，λ1、λ2、λ3和λ4分别为4个优化目标的权重系数，满足λ1+λ2+λ3+λ4=1，本文取λ1=0.3，λ2=0.3，λ3=0.2，λ4=0.2。以《电车牵引计算规程》为依据[16]，优化模型约束条件为式(1)描述的电车动力学方程以及电车安全因素t(0)=0，t(S)=T，v(0)=v(S)=0，v(s)

进行多目标优化时，电车的低能耗、高正点率、站台停靠准确性以及高乘客舒适度需要适应的函数值尽可能小，本文选取适应函数fitness(f)如式(11)所示。

fitness(f)=F=min[λ1F1+λ2F2+λ3F3+λ4F4]=

(11)

2 基于混沌免疫微粒群算法的电车运行过程多目标优化

2.1 基本微粒群算法

PSO算法是将每个个体看作n维搜索空间中的一个没有质量和体积的微粒，并以一定的速度飞行，在此过程中保存每个个体微粒的最佳位置以及所有微粒经的最佳位置，个体微粒与群体微粒之间实时的进行信息交互，从而使微粒移动至全局最优的位置，此时即为最优解。本文采用带有惯性因子的改进微粒群算法，可由式(12)和式(13)表示

v(i+1)，j=ωvi，j+c1rand()(pBest-xi，j)+

c2rand()(gBest-xi，j)

(12)

x(i+1)，j=xi，j+v(i+1)，j

(13)

式中，“i”代表微粒i；“j”代表微粒的第j维；t代表第t代；pBest代表第i个微粒所经历的最佳位置；gBest代表所有微粒所经历的最佳位置；c1为微粒的自学习因子；c2取值范围为0～2，即微粒群的学习因子；rand()的取值在(0，1)随机中选取；ω为惯性权重，较大的ω有较好的全局收敛能力，而较小的ω有较强的局部收敛能力，研究表明，采用式(14)表示的线性递减法调整权重因子能提高算法的优化能力。

(14)

式中，tmax为最大迭代次数；ω∈[ωmin，ωmax]，根据专家经验ωmin取0.4，ωmax取0.9。

2.2 CIPSO优化算法对模型的求解

为避免PSO算法在进化过程中易出现早熟收敛现象的发生，采用混沌Tent映射初始化粒子群，再将免疫算法中的疫苗接种应用到PSO算法当中，构成新的智能算法。

CIPSO(Chaotic Immune-vaccine Particle Swarm Optimization，混沌免疫微粒群优化)算法首先从混沌空间要把混沌变量映射到解空间，让一小部分微粒的飞行速度具有遍历性和随机性等特点，因为这一小部分微粒在混沌化之后就可以避免陷入局部最优，有效地减小进化过程中微粒出现的早熟收敛现象，从而寻找到全局最优值[17]。采用如式(15)所示Logistic混沌模型产生混沌变量[18]。

Xn+1=L(μ，Xn)=μXn(1-Xn)n=0，1，2，…

(15)

其中，Xn∈[0，1]；μ∈[0，4]为控制参数，当μ=4且Xn不等于0.25、0.5、0.75时，Logistic映射是混沌不变集。

接着将所求目标模型(10)式抽象为免疫接种算法中的抗原，将需求解的电车最优控制策略抽象为抗体，全局最优值gBest对应于免疫接种算法中的疫苗。而后调整对待求问题的解，让解的质量得到提高，接着引入免疫选择机制，增大搜索速度，可以更快地找到最优解。确定接种疫苗概率是疫苗接种算法的核心，选择接种疫苗概率时，更偏向于选择接种疫苗概率较大的微粒，这样可以使得到的适应度值更小，接种后的微粒接近全局最优值gBest(即疫苗)。本文的接种疫苗概率p按式(16)计算[19-20]。

(16)

其中，fgen为准备接种粒子的适应度值。

对城市有轨电车中电车运行操纵过程进行优化时需确定初始输入控制序列，该初始序列按照《电车牵引计算规程》要求并结合实际区段线路参数获得，设该输入控制序列为{ui}，i=1、2、…、k，该控制序列下走行的距离为{si}，i=1，2，…，k。

CIPSO优化算法的基本流程如图1所示。

图1 CIPSO算法流程

3 仿真验证与结果分析

本文选取城市有轨电车作为研究对象，以现场试验段实际线路及相应电车参数进行仿真研究，为了验证CIPSO算法对电车运行控制策略多目标优化的有效性。由于本次仿真所采用的数据为试验段数据，站间距离较短，根据该试验段实际情况，选取其中两站距离大小较长长度700 m的线路进行城市有轨电车运行仿真验证，电车运行线路参数如图2所示，电车自身的参数特性如表1所示。

图2 线路参数

参数名称参数特性电车总质量/t90最高运行速度/(km/h)100紧急制动距离/m30:v=26km/h220:v=70km/h340:v=100km/h基本阻力/kNω′0=2.25+0.0190v+0.000320v2牵引特性/kNF=234-0.2502v(026km/h)制动特性/kNb=570×(2×v+150)/(3×v+150)紧急制动b=406×(2×v+150)/(3×v+150)130kPab=285×(2×v+150)/(3×v+150)80kPa

在仿真验证中电车的运行时长为97 s，容许早晚点时间范围为10 s。采用的CIPSO优化算法选取的微粒群大小为200，迭代的次数设置为100次，实验采用Matlab脚本语言编写代码进行仿真实验。为了证明本文采用方法的优越性，分别采用了CIPSO算法与CPSO(Chaotic Particle Swarm Optimization，混沌微粒群优化)算法、IPSO(Immune-vaccine Particle Swarm Optimization，免疫微粒群优化)算法对多目标模型进行优化，各种方法的优化结果如图3所示。分析图中各适应度值的变化曲线可以得出3种算法的收敛速度排序为：CIPSO算法>CPSO算法>IPSO算法。

图3 适应度变化曲线

在仿真过程中，首先采用实际运行策略控制城市有轨电车，其相应的控制策略如图4所示。

图4 优化前控制策略

从图4可见，电车在大部分时间内均在接近限速的最大速度下运行，并且从曲线变化频率可以看出，电车工况频繁转换，以此方式控制电车，电车运行全程时间很短仅90 s，但由于电车的运行特点使得其能耗指标达到147.16 kW·h，此时电车全程的运行距离为647 m，因为工况的连续转换，在电车运行过程中乘客乘坐的体验感很差，电车在实际运行策略下4个优化目标的评价指标参数值如表2所示。

表2 实际运行策略下的评价指标参数

图5 CIPSO优化后控制策略

图6 CIPSO优化后速度距离曲线

鉴于实际运行控制策略下对节能、正点、停靠准确和乘客舒适度4个方面的提高并不理想，本文采用CIPSO算法优化多目标的运行模型，得到了如图5所示电车控制策略，其控制序列为 (1，0，1，0，1，0，-1，0，-1)，电车在该控制序列下在区间走行的距离(m)如图6所示，为：(93，117，69，101，54，109，48，61，31)，分析图6中的速度距离曲线，可知电车在运行过程中大多数时间并没以最大速度运行，在经过CIPSO优化后的控制策略下电车的运行过程有很大的改变，控制及运行的灵活性更强，并且在此控制策略下电车能够充分利用在区间的运行时分。通过对速度距离曲线的分析并结合图2给出的线路数据，在运行至230，340 m处存在48‰下坡以及53‰上坡，在速度曲线上可以看到，处于下坡时，电车为制动状态，速度有一定程度的降低，处于上坡状态时电车速度在牵引状态下有一定的上升，但上升幅度不大，曲线出现了较小范围的波动。从整体上分析，CIPSO优化后的控制策略下电车全程运行时间为95s，能量消耗为77.33 kW·h，此时电车全程的运行距离为693 m，乘客乘坐体验感很好，在此种控制策略下4个优化目标都能得到较好的结果。对CIPSO优化后控制策略的性能进行分析，结果如表3所示，其中用“+”表示性能的增大，用“-”表示性能减弱，经CIPSO优化后的控制策略下，电车在同一线路条件下运行，4个优化目标的指标评价结果都有较大幅度的提升。

表3 CIPSO优化后的评价指标参数及性能分析

本文还采用了文献[6]中提出的ADPSO算法在相同条件和环境下对本文建立的多目标模型求解，得到如图7和图8所示的电车控制策略及速度距离曲线。由图7可见，经ADPSO算法优化后比CIPSO算法优化后的“牵引-惰行-制动”工况转换更频繁，由于ADPSO算法本身存在的易陷入局部最优的缺点，会使经由ADPSO算法优化后控制策略下电车的运行工况存在较大波动，所优化的4个指标中电车的性能及乘客舒适度有较大的影响，CIPSO优化后的结果更佳。

图7 ADPSO算法优化后控制策略

图8 ADPSO算法优化后速度距离曲线

在经过ADPSO算法优化后，城市有轨电车的运行时长为91 s，能耗为83.65 kW·h，运行距离为662 m，乘客的不舒适度指标为34.58。采用ADPSO算法优化后的电车的运行能耗、区间运行时间误差、停车误差以及不舒适度的评价指标参数值及性能分析如表4所示。表4中，从性能分析结果可以看出经过ADPSO算法优化后，4个指标在性能上均有一定的提高。但与表3中的结果进行对比，所优化的4项目标，其性能提高相对较少。经ADPSO算法优化后，电车的全程运行时间更长，能耗更高，电车的停靠准确性以及乘客舒适度更低。

表4 ADPSO优化后的评价指标参数及性能分析

4 结论

(1)通过对城市有轨电车中电车运行多目标优化问题的分析，以电车安全因素以及电车运行动力学方程为约束条件，同时对电车能耗、正点率、停靠准确性、乘客舒适度等指标进行优化，建立了相应的数学模型。针对粒子群算法的缺点，引入混沌映射、免疫接种和免疫选择对其进行改进，提高了算法的全局搜索能力及搜索精度。

(2)根据城市有轨电车的运行特点，进行了实例仿真。结果表明，加入混沌映射、免疫接种和免疫选择算法优化的PSO算法能够实现对城市有轨电车运行过程的多目标优化，并与ADPSO优化算法进行比较，进一步验证本文提出的CIPSO算法在优化城市有轨电车控制策略时的可行性及有效性。