基于再生制动的城市轨道列车节能控制研究

厉 高，林建辉，庄 哲，何 刘

（西南交通大学 牵引动力国家重点实验室，四川 成都 610031)

0 引言

随着城市交通的发展，城市轨道交通快捷、准时、安全、高效等优点逐渐凸显，使得越来越多的居民出行选择城市轨道交通[1]。同时，随着列车运行速度的提高，列车的运行能耗也明显增大，因而在满足运行时间的条件下，对城市轨道列车节能运行的研究不仅可以促进低碳经济的发展，还能降低列车运营成本，具有重大的经济意义。

目前，国内外许多学者致力于研究城市轨道列车的节能优化问题。牟瑞芳等[2]将列车能耗最小值问题转化为寻找一系列满足约束条件的目标速度及速度集合问题；Liu等[3]采用极大值原理，求解列车节能策略集合，并采用数值算法对集合中的列车工况转换点进行计算；朱金陵等[4]采用极大值原理应用于模型求解，并结合列车操纵经验给出了列车节能算法；宋文婷等[5]通过遗传算法搜索最优的速度码组合序列，获得速度操纵范围；刘炜等[6]通过最大值原理得到列车节能最优控制工况集，提出分段处理列车运行区间方法。为此，提出将列车惰行时间进行动态分配，达到列车定时节能的目的，并设计开发城市轨道列车节能运行仿真平台，以佛山南海低地板列车为例，通过仿真结果与实际运行能耗数据相比较进行可行性验证。

1 再生制动下的城市轨道列车节能最优控制模型

列车的再生制动是指在发电机的工作工况下，牵引变流器将牵引电机产生出的三相交流电整流为直流电，并反馈回电网进行储存或利用。由于城市轨道交通站间距离较短，因而列车的起动及制动十分频繁。为了实现列车节能运行，列车在制动停车时主要采用再生制动，当再生制动力不足或失效时，才会使用机械制动或空气制动进行补足或替代。列车在制动过程中会产生巨大的再生制动能量，其原理是将电动机切换成发电机运转，进而将车辆的一部分动能转化成电能进行储存或利用，因而再生制动对城市轨道列车节能控制具有重要意义。

城市轨道列车节能最优控制是指在准时、安全的基础上，列车在运行过程中实现节能的目的，即列车在运行过程中所消耗的能量最小。在满足给定运行时间及运行距离的前提下，结合最优控制原理，对列车节能运行进行求解，使其能耗最低。在考虑列车再生制动的基础上，其节能优化的目标函数可表示为

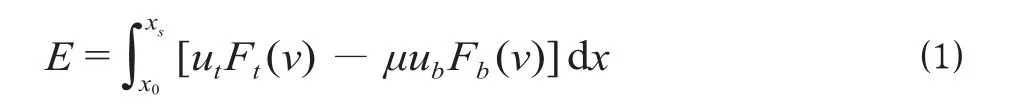
式中：E为列车在运行过程中的能量消耗；ut为列车的牵引手柄级位信息，0≤ut≤1；ub为列车的制动手柄级位信息，0≤ub≤1；x0为列车节能优化起点公里标；xs为列车节能优化终点公里标；μ为列车在制动工况下，其再生制动反馈能量的效率；Ft(v)为列车运行速度为v时所对应的列车能发挥的最大牵引力；Fb(v)为列车运行速度为v时所对应的列车能发挥的最大电制动力。

在线路运行过程中，城市轨道列车的运行过程可以表示为

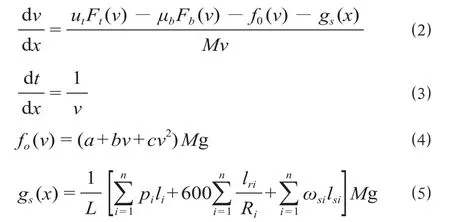
式中：f0(v)为列车的基本阻力，是列车在运行过程中所受到的空气阻力及轮轨摩擦力等，并在列车的运行过程中不受线路影响，一直都存在的力；gs(x)为列车的附加阻力，是列车在运行过程中的坡道附加阻力、曲线附加阻力及隧道附加阻力等合力，由线路中的坡道、曲线及隧道引起；M为列车的总质量[7]；a，b，c分别为列车的基本阻力公式系数；pi，li分别为线路中第i个坡道的坡道千分数及被列车覆盖的坡道长度；Ri，lri分别为线路中第i个曲线的曲线半径及被列车覆盖的曲线长度；ωsi，lsi分别为线路中第i个隧道的单位隧道阻力系数及被列车覆盖的隧道长度。

同时，列车在运行过程中还受到以下约束条件限制。

式中：v(x)为列车在公里标为x处的运行速度；V(x)为列车在公里标为x处的限速；t(x0)为列车在起点的时刻；t(xs)为列车在终点的时刻；T为在列车时刻表中规定的列车运行总时间。

结合公式⑴至公式⑺，根据牵引计算分析，结合最优控制原理，总结得出以下列车的运行工况有利于节能：①在列车运行时间一定的基础上，其牵引速度震荡越小，基本阻力所造成的能耗越小，即时间一定时保持匀速运行最节能；②在列车启动阶段，在不考虑舒适性的前提下，列车以最大加速度加速可减少阻力做功，有助于节能；③在列车制动阶段，在不考虑舒适性的前提下，列车以最大制动能力制动可减少制动时间，有助于节时及减少能耗；④为了达到节能的目的，在制动工况前，列车适当的惰行对于减少列车节能是非常重要的，可以减少列车运行中的动能损失；⑤在列车下坡阶段，为了减少能量消耗，尽量减少列车的制动。

基于以上分析，列车节能最优控制操作策略原则如下：①列车启动阶段全力牵引，ut= 1，ub= 0；②列车达到限速后转为巡航，ut∈ (0，1)，ub= 0或者ub∈ (0，1)，ut= 0；③列车制动前惰行，ut= 0，ub= 0；④列车全力使用电制动，ut= 0，ub= 1。

2 城市轨道列车节能最优控制算法

基于节能最优控制模型，给出从甲站到乙站最优操作为全力牵引、巡航、惰行、全力使用电制动。列车节能最优过程示意图如图1所示。

图1 列车节能最优过程示意图Fig.1 Schematic diagram of the optimal process of train energy saving

当线路拥有多个限速区段时情况更为复杂，多限速区段下的列车节能最优控制过程示意图如图2所示。图2中，x0x1，x1x2，x2x3，x3x4，x4x5分别代表5段限速区段，Vi代表不同限速区段的限速值。列车在每个由高限速区段到低限速区段的减速首先采用惰行，后再采用全力电制动，其他区段优化操作序列不变；如果列车在高限速区段过渡到低限速区段减速采用惰行直接减速到低限速区段的限速，则保持此速度巡航运行至低限速区段。

图2 多限速区段下的列车节能最优控制过程示意图Fig.2 Schematic diagram of the optimal control process of energy saving in multi-speed limits section

由图1和图2可知，列车优化操作可以转化为找出巡航至惰行的转换点及惰行至制动的转换点，即寻找图1中A，B两点坐标。基于时间逼近搜索方法搜索优化区间，提出一种将惰行时间动态分配的方法，得到节能最优控制模型。节能最优控制模型求解算法步骤如下。

步骤1：对列车使用最大运行策略进行仿真，计算列车运行通过该区间的时间t0。

步骤2：搜索区间内由高限速过渡到低限速的区段，如图2中的x1x2段到x2x3段便是需要寻找的高限速过渡到低限速的区段。

步骤3：记录列车在最大运行策略下“巡航→制动”转换点的坐标 (xi1，ti1)，(xi2，ti2)，…，(xij，tij)；如果不存在这样的区段，如整个区间距离短，列车未经历巡航工况，则跳转至步骤7。

步骤4：由步骤3中的所有高限速过渡到低限速区段中的“巡航→制动”转换点，转换点时间向前移动一个步长ΔT，相应计算出列车在该时刻到达的坐标 (xi1- Δx1，ti1- ΔT)，(xi2- Δx2，ti2-ΔT)，…，(xij- Δxj，tij- ΔT)，并由这些坐标分别开始转换工况为惰行。

步骤5：如果在惰行工况时，列车速度变大，则列车使用电制动，继续保持巡航工况；如果速度下降，则惰行至与列车最大运行策略中制动曲线相交，取交点为“惰行→制动”转换点。列车节能优化更新过程如图3所示。

图3 列车节能优化更新过程Fig.3 Train energy saving optimization update process

步骤6：通过调整列车运行策略，不同区段下列车运行时分比节时策略分别增加Δt1，Δt2，…，Δtj，并计算不同区段下列车运行消耗能量ΔE1，ΔE2， …，ΔEj， 通 过 比 较 ΔE1/Δt1，ΔE2/Δt2， …，ΔEj/Δtj选择列车节能最优控制过程。节能最优控制算法流程图如图4所示。

步骤7：当列车处于进站区段优化时，如果惰行工况下，使得列车停车却仍没有到站，则删除该工况，并转到步骤4。

步骤8：每更新一次列车运行方式，更新列车运行图像，如图3所示，更新后列车运行图像曲线为“O→M→A→B→S”。列车运行时分增加Δt后，如果满足时 (Δt(i)为第i次更新曲线后，列车运行时间的增量值；n为列车总共更新曲线次数；T为给定列车运行时间；δ为列车运行时间能够接受的时间误差极限)，则继续向前移动一个步长，并返回步骤5；如果列车满足时，则停止优化，并得到优化曲线。

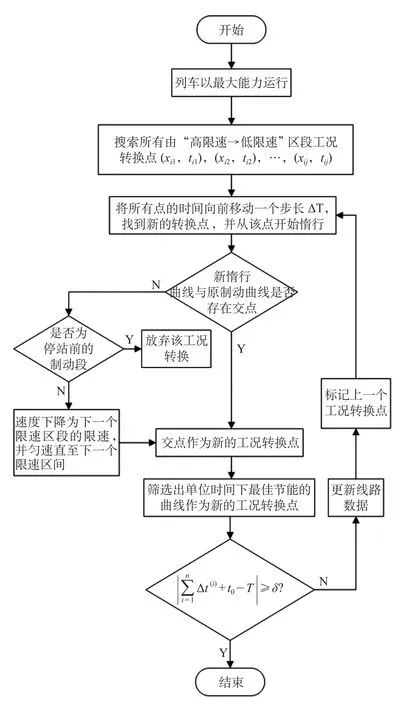
图4 节能最优控制算法流程图Fig.4 Flow chart of energy saving optimal control algorithm

3 仿真验证及实例分析

为进一步验证节能最优控制算法的可行性，使用列车牵引仿真计算模型，并结合“佛山南海”线路仿真数据，以低地板铰接式城轨列车建立仿真列车模型，设计列车节能仿真运行平台[8]，该平台是基于Visual Studio2010开发环境与MFC框架开发，同时考虑线路中坡道、曲线及限速影响，以及列车对再生制动能源的回收，组成一个比较完善的城轨列车节能运行仿真平台。列车相关参数如表1所示。

选择运行线路为“大坊站—泰山路站”，两站站间距约为1.748 km，该段限速转换较多，具有显著特征，因而选该段作为仿真区间，两站实际运行时间为137 s，允许误差为±3%以内，列车运行能耗为13.88 kW·h，再生制动能量为2.24 kW·h，列车总能耗为11.64 kW·h。列车仿真运行数据如图5所示。通过列车优化运行仿真得出，列车仿真的时间为140.2 s，仿真运行的能耗为11.27 kW·h，再生制动能量消耗为1.67 kW·h，消耗总能耗为9.61 kW·h，列车运行所能减少的能量占列车实际运行总消耗的能量的17.44%，列车运行能耗明显降低。

图5 列车仿真运行数据Fig.5 Train simulation operation data

以上分析均基于搜索优化区间动态分配惰行时间的情况。作为对比，未动态分配的仿真运行数据如图6所示。通过图6可以得出，列车仿真计算时间为140.3 s，仿真计算能耗为12.39 kW·h，再生制动能量为1.98 kW·h，消耗总能耗为10.41 kW·h。列车运行减少的能量占列车实际运行总能耗的10.57%。

节能最优控制算法采用牵引惰行相结合工况，在避免不必要制动的基础上，采用时间逼近搜索算法搜索优化区间，搜索各个惰行点，对惰行时间进行动态分配。经仿真，节省能量占未动态分配惰行时间仿真运行能耗的7.68%，从而达到节能最优的目的，验证了节能最优控制算法的可靠性。

4 结束语

随着列车运行速度的提升，能耗会明显增大，研究城市轨道列车节能运行，对列车惰性时间的有效分配、能量利用率的提高、车辆运行成本的降低具有重要意义。构建城市轨道列车节能最优控制模型，得出列车节能优化操纵最优序列，仿真验证结果表明节能效果显著，为城市轨道交通节能运营提供理论参考。为更好地发挥节能最优控制算法的优势，应进一步探究多车相互作用、列车过叉及乘坐舒适性要求等因素的影响，以提供更加节能、舒适的轨道交通出行服务。

图6 未动态分配的仿真运行数据Fig.6 Simulation run data not dynamically allocated