带柔性重叠时间窗编组站终到列车到发线优化研究

黄俊生，广晓平

（兰州交通大学 交通运输学院，甘肃 兰州 730070）

0 引言

编组站是我国铁路的运输枢纽，主要进行列车解体和编组等技术作业；同时作为列车“加工车间”，其运转效率直接影响铁路列车周转效率。无论是客运站还是技术站，到发线的高效运用都是行车作业的核心环节[1]。到发线的运用负荷，是反映车站到达场对运行图适应能力的重要指标之一[2]，同时到发线分配是否可行也是反映铁路日常工作效率的指标之一。由于到发线的运用受不确定因素影响较多，如列车到发不确定[3]、技术作业时间不确定、车辆等级和种类繁多[4]等，因而到发线的运用研究更为复杂，构建的目标模型也具有多种形式。龙建成等[5]构建以作业晚点时间最短、各进路总走行时间最短的多目标规划模型；张英贵等[6]采用排序理论方法，构建车站股道运用的排序模型；刘伟等[3]根据列车到发不确定性，构建车站咽喉利用和股道分配优化模型。

由于该类问题多为NP问题，因而大大增加了求解难度，此类问题的求解多采用启发式进化算法。郭莉等[7]运用遗传算法对到发线运用进行优化；康柳江[8]运用模拟退火算法计算福州站进出站咽喉时间、股道占用分配等问题。编组站到发线的运用可看作特殊的柔性车间调度问题[9]，列车加工顺序将对股道运用产生重要影响。

目前，同时考虑列车到达时刻不确定、到达场技术作业时间弹性、终到列车选择股道多样性及带重叠时间窗4种随机因素的研究较少。为进一步提高编组站到发线的运用效率，构建带柔性重叠时间窗约束、以股道最大占用时间最小化为目标的非线性规划模型，由于此类问题已被证明为NP-hard问题[10]，为在有限时间资源内搜寻到模型的满意解，设计模拟退火算法对该模型进行求解计算。

1 柔性和重叠时间窗

股道分配运用问题可以看作是传统车间调度问题的衍生，由于编组站到发线使用更灵活，因而股道分配运用问题有别于传统车间调度问题。终到列车股道分配问题建立在柔性和列车到达有重叠时间窗的基础上，考虑的柔性可以理解为完全柔性，有别于部分柔性和传统问题。完全柔性体现在列车到达时刻不确定，技术作业时间有弹性及终到列车选择股道多样性3个方面。因此，考虑完全柔性的股道分配更贴近编组站实际工作安排。完全柔性、部分柔性和传统问题区别如表1所示。

表1 完全柔性、部分柔性和传统问题区别Tab.1 Difference among fully flexibility, partial flexibility and traditional problems

在编组站实际工作中，多列终到列车到达时刻和列车从股道清空时刻的时间窗存在互相重叠的现象。重叠时间窗是指2 (多)列终到列车的到达时刻和列车从股道清空时刻的时间窗存在重叠，若2(多)列列车一旦存在“重叠时间窗”关系，则2 (多)列列车在重叠时间窗内不能占用同一股道。重叠时间窗关系如图1所示。

图1 重叠时间窗关系Fig.1 Relationship of overlapped time window

因此，以编组站终到列车为对象，以到发场股道为资源，构建以股道最大占用时间最小化为目标、带柔性重叠时间窗约束的非线性规划模型。

2 带柔性重叠时间窗非线性规划模型

2.1 变量定义

I为终到列车集合，任意列车i∈I，I= {i|i= 1，2，…，n}，n为某阶段计划内编组站接进的终到列车数量；J为编组站到发线股道集合，编组站内到发场任意到发线j∈J，J= {j| 1，2，…，m}，m为编组站到发线数量。

为0-1变量，表示列车i在t时刻是否占用j股道，如果= 1则表示列车i在t时刻占用j股道，否则= 0；为列车i占用股道j的实际结束时刻；为列车i占用股道j的实际开始时刻；为列车i占用股道j的计划开始时刻；pi为列车i在股道j的技术作业时间；Nj为股道使用均衡系数；，为偏差系数，> 1 对应列车晚到，0 ＜＜ 1 对应列车早到，> 1 表示技术作业时间延长，0 ＜＜ 1表示技术作业时间缩短；Tmin为同一股道接近列车最小安全时间间隔，设为14 min；M为一个无穷大的数。

2.2 约束条件

（1）股道占用约束。同一股道在同一时刻只能由一列车占用或不占用，计算公式为

（2）列车占用股道约束。同一列车在同一时刻只能占用同一股道，计算公式为（3）重叠时间窗约束。重叠时间窗内连续2趟列车不能占用同一股道，计算公式为

（4）股道占用最小时间间隔约束。最小安全时间间隔如图2所示。前后2列车占用同一股道，应保证后续列车i的接车时刻与前续列车i'从股道清空时刻之差大于最小安全时间间隔Tmin，否则= 0，计算公式为

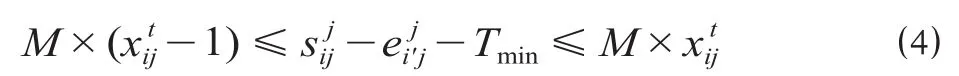
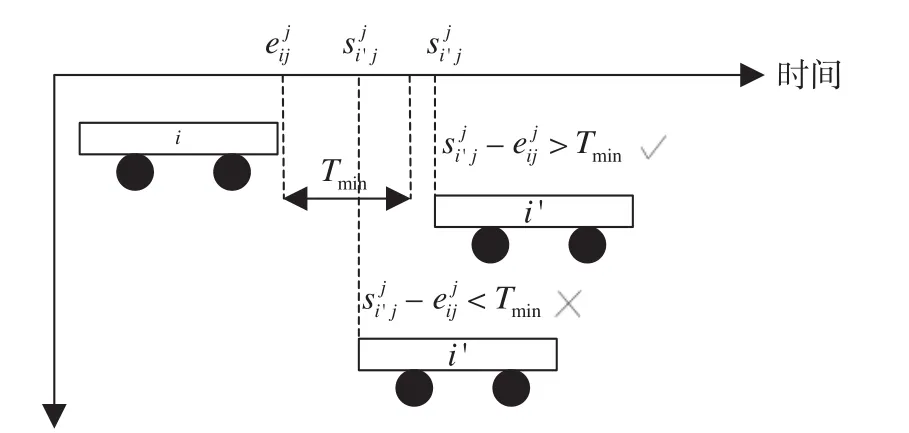
图2 最小安全时间间隔Fig.2 Minimum safety time interval

（5）股道使用均衡性约束。采用占用股道次数定义股道使用均衡性。为方便描述，将各到发线的占用次数与到发线平均占用次数之差的平方和定义为股道使用均衡性，Nj为股道使用均衡系数，计算公式为

已有研究[3]认为股道使用均衡系数越小，股道使用均衡性越好；股道使用均衡系数越大，股道使用均衡性越差。

（6）终到列车实际到达与清空股道时刻。为表示列车实际到达时刻，引入偏差系数，该值可用于调整列车到达时刻，计算公式为

终到列车实际从股道清空时刻等于终到列车实际到达时刻加上实际技术作业时间。为体现弹性技术作业时间，引入偏差系数，用于调整技术作业时间。

（7）股道占用时间。股道占用时间由3部分组成，分别是终到列车到达技术作业使用时间ti1，终到列车等待列车检查作业时间ti2，终到列车等待解体作业时间ti3。

2.3 目标函数

由于编组站站线资源紧张，应尽可能保证到发线能力富足，且合理分配股道，使到发线最大占用时间最小化，提高股道资源使用率，进而减少维修成本，优化目标函数为

2.4 模拟退火算法

带柔性重叠时间窗的终到列车股道应用问题属于柔性车间调度问题的衍生，属于NP-hard问题，使用传统数值计算方法解决此类问题将很难在有限时间内得到满意解。江秀等[11]列举了解决此大类问题的常用智能算法有遗传算法、蚁群算法、禁忌搜索算法、模拟退火算法等；Zhu等[12]设计了基于agent的启发式算法对车站线路进行调度优化。由于列车占用股道资源的起始时刻和占用股道资源的时间均不确定，使得合理调配股道资源模型的求解存在较大困难。因此，结合模型复杂性、多样性和特殊性的特点，选用模拟退火算法求解此问题。

模拟退火算法参照固体物理退火过程，当温度较高，分子运动剧烈，分子内能增大随着温度降低，分子也逐渐停止运动，趋于有序。因此，使用该算法求解大型组合类[1]NP问题能够避免求解结果陷入局部最优解，而使最终结果趋于全局最优。

模型中的为0-1决策变量，因而算例的模拟退火算法采用该编码方式表示列车与股道的关系。结合已构建的带柔性重叠时间窗模型的特点，设计模拟退火优化算法具体流程步骤如下。

步骤1：①输入初始温度T、降温系数α、最小时间间隔，设定外部循环阈值outIteration、内部循环阈值inIteration；②产生初始解 ，初始解为初始股道分配方案，判断初始解是否满足公式⑴—⑸的约束条件，不满足则重新生成，直到满足约束条件；计算f(i)，f(i)表示初始股道分配方案对应的股道占用总时间，并且设定a= 1，b= 1。

步骤2：①如果达到内部循环停止条件，转步骤3；②否则，父代通过交换某列车的股道得到新的子代解，两父代通过交叉产生2个新的解，判断是否满足公式⑴—⑸的约束条件,不满足则重新生成，直到满足约束条件；③取其中一个子代解j，计算f(j)，f(j)表示新股道分配方案对应的股道占用总时间，如果f(j) -f(i) ＜ 0，则表示新的分配方案目标值优于初始解目标值，则i=j；如果f(j) -f(i) > 0，则计算exp (- (f(j) -f(i)) /T)，如果存在exp (- (f(j) -f(i)) /T) >rand(0，1)，则以概率的形式让i=j，b=b+ 1，转①。

步骤3：①如果达到外部循环停止条件，终止运算；②否则，转步骤2，a=a+ 1。

3 算例分析

参数设置：模拟退火算法外部循环设置为1 000次，内部循环为5次，初始温度为100℃，降温系数为0.85，最小时间间隔设为14 min。

为验证模型的正确性和合理性，现以某三级六场编组站接进终到列车为例进行验算。该编组站下行到达场有12条股道，其中1股为正线，不进行接发列车作业，2-12股道可进行接发列车作业。为降低算例复杂性，终到列车接进股道不受其他种类列车的影响。编组站下行到达场股道布置如图3所示。

图3 编组站下行到达场股道布置Fig.3 Tracks arrangement of downward receiving yard

经统计，终到列车技术作业时间均值统计如表2所示。

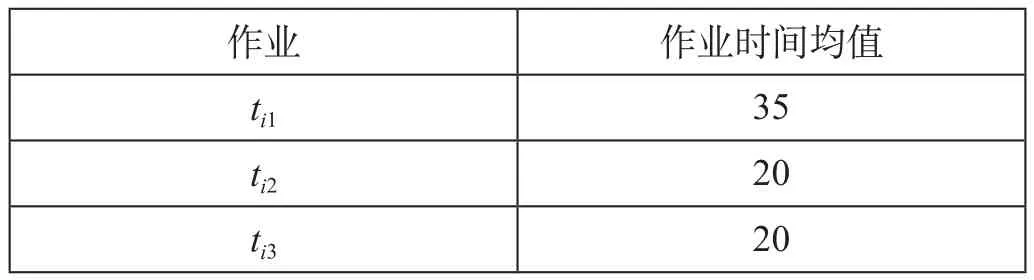
表2 终到列车技术作业时间均值统计 minTab.2 Average technical operation time of arriving trains

以某天下行到达终到列车接车计划为例，经统计得到该天下行终到列车的计划接入到发线时刻和列车计划从到发线清空时刻，其中5号和6号列车、10号和11号列车、14号和15号列车、21号和22号列车接入到发线时刻和从到发线清空时刻存在重叠时间窗关系，阶段计划接近列车时刻和计划清空股道时刻如表3所示。

3.1 算例1

编组站到发线占用计划安排是在不考虑列车发生意外条件下对股道进行的初始安排，因此，算例1优化不考虑列车早到、晚到、或技术作业延长(缩短)等情况。结合编组站到发线占用计划安排特点，以某天到发线初始占用计划安排为例，运用模拟退火算法对原始股道分配方案进行优化，优化前后的股道分配对比如表4所示。

相较于到发线占用计划安排，优化后股道总占用时间由149 min减少至109 min，股道总使用时间减少了40 min。进一步得到算例中股道占用时间迭代曲线如图4所示。

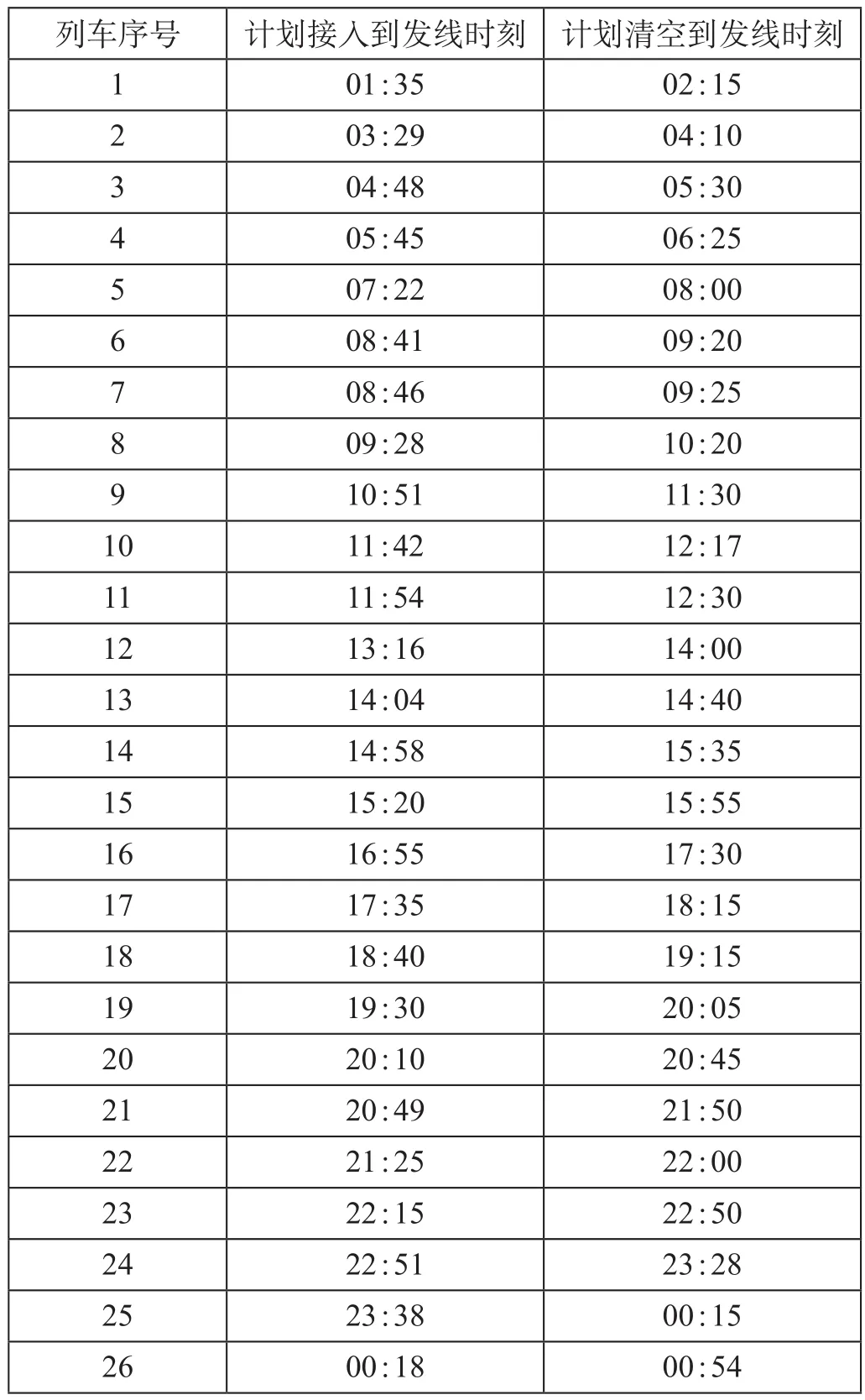
表3 阶段计划接近列车时刻和计划清空股道时刻Tab.3 Time of approaching trains and empty tracks under periodic plan

3.2 算例2

到发线占用计划安排并未考虑编组站终到列车实际到达时间和实际技术作业时间的不确定性，一旦发生列车晚点等意外情况，将对编组站正常作业产生严重影响，为提高到发线分配的鲁棒性，考虑部分终到列车早到、晚到或有技术作业延长或缩短的复杂情况，对原始股道占用计划安排进行优化。

参照文献[2,8]列车到发时间不确定的判断依据，到发时间偏差系数的波动范围设定为0.9≤≤1.1；根据实际工作经验，实际技术作业时间应在原技术作业时间上小幅度摆动，因此，技术作业时间偏差系数的波动范围设定为0.9≤≤1.1；均衡系数设定为Nj= 2.9。

表4 优化前后的股道分配对比Tab.4 Comparison of tracks allocation before and after optimization

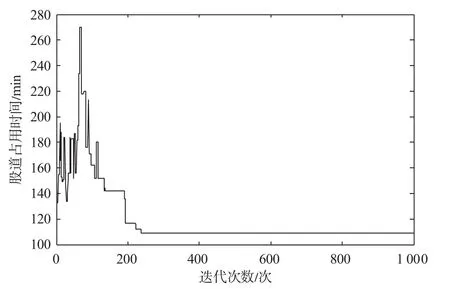
图4 股道占用时间迭代曲线图Fig.4 Iteration graph of occupation time of tracks

为降低求解复杂性，列车早到(晚到)与技术时间延长(缩短)并不同时出现在同一列终到列车上；且发生早到(晚到)或技术时间延长(缩短)的终到列车均在随机条件下进行设定。

经计算，优化前后股道分配方案比较如表5所示。

表5 优化前后股道分配方案比较Tab. 5 Comparison of tracks allocation before and after optimization

经计算，在到发线占用计划安排条件下，股道总占用时间为189 min，优化后股道总占用时间为125 min，股道总使用时间减少了64 min，股道的使用效率得到有效提高。

结合算例1和算例2可知，优化前到发线占用时间由149 min增加至189 min，增加了40 min；优化后到发线占用时间由109 min增加至125 min，增加了16 min。模型优化了编组站到发线对外界的干扰的适应性，因而股道分配的鲁棒性得到提高。

3.3 算例3

股道均衡系数越大，即占用某股道的次数越多，股道使用的均衡性越差。算例1和算例2的股道均衡系数均设定为Nj= 2.9，算例3对列车正常到达下的股道均衡系数进行灵敏度分析。不同均衡系数下优化前后股道总占用时间对比如表6所示。

表6 不同均衡系数下优化前后股道总占用时间对比Tab.6 Comparison of occupation time of tracks before and after optimization under different balanced parameters

由表6可知，优化后的股道总占用时间明显降低，且股道不均衡系数对终到列车占用到发线总时间影响较小，在编组站到发线运能紧张的情况下，增加某股道使用频次不会对到发线占用总时间产生显著影响。

4 结束语

编组站到发线运用计划直接优化目标是在减少列车进路交叉前提下，保证不间断接发列车，因而编组站到发线优化研究，可以有效保证编组站进行日常有序技术作业。在研究过程中，引入柔性重叠时间窗，建立以股道占用最大时间最小化为目标的非线性规划模型。仿真算例1和算例2得到的优化方案提高了到发线利用率和到发线分配的鲁棒性，表明所构建的模型和算法具有可行性和合理性，算例3的结论认为增加某股道的使用频次可以缓解编组站到发线运能紧张的状况。考虑到列车等级和列车种类也会对股道分配产生影响，如何在更复杂的条件下分配编组站到发线还需要进一步的研究。