废水处理系统的动态过程监测

刘鸿斌 陈 琴 张 昊 杨 冲

(1.南京林业大学林业资源高效加工利用协同创新中心，江苏南京，210037;2.华南理工大学制浆造纸工程国家重点实验室，广东广州，510640)

随着我国经济的高速发展，工业生产不断向规模化、复杂化、自动化的方向快速发展，工业生产中所需测量的变量逐渐增加［1］，且故障检测过程表现出高度非线性、时滞性等特征［2］，使得实际生产过程中出现故障甚至发生事故的可能性也随之增加，因此有效的系统检测和故障诊断对系统控制尤为重要［3］。近年来，基于多元统计分析的故障诊断方法已广泛应用于工业过程检测，然而随着生产过程的快速发展，连续生产所带来的时变性成为过程检测中的一大难题［4-6］。故障检测过程中的动态特性体现在变量之间以及变量与采样时间之间的相关性，传统的多元统计方法对于动态过程不能进行准确的检测［7］，因而故障检测中存在较大的偏差，且存在误检、误报等情况。因此在检测中解决工业生产过程中所存在的动态特性问题变得尤为重要。

多元统计方法是利用多变量之间的相关性进行诊断，常用的方法包括主元分析法 (Principle Component Analysis，PCA)、最小偏二乘法 (Partial Least Squares，PLS)、独立元分析法 (Independent Component Analysis，ICA)以及费舍尔判别分析法(Fisher Discriminant Analysis，FDA)。传统的PCA是将高维度数据投影至低维度的子空间，在尽量较小的维数中保留原空间的最大方差，以此来保留数据中的主要信息。然而，PCA在处理具有非高斯、非线性和强动态特征的数据时不能准确地解释变量间的关系［8-11］。与PCA不同的是，ICA是将多元数据用线性组合的方法，得到统计独立以及服从非高斯分布的潜变量，即独立元 (Independent Component);且在建模的过程中ICA涉及到了更为高阶的统计量，所以与PCA相比，在面对非线性数据时ICA具备更高的鲁棒性。然而，传统PCA及ICA方法故障检测是以采样点之间的相互独立为前提，但实际的生产过程几乎不会处于稳定状态，因此传统PCA、ICA等静态方法在过程故障检测中的准确性大幅下降，同时也存在较高的误报率。

对于故障检测过程采样点间存在的动态特性，Ku W等人［12］在1995年首次提出了动态主元分析(Dynamic Principle Component Analysis，DPCA) 的方法，在模型建立过程中使用时滞移位的动态主元分析法。DPCA考虑到故障检测过程中数据序列的相关性，引入时滞变量l，构建增广矩阵，以此来克服实际工业过程中存在的时变性，再通过统计量指标T2和SPE对故障检测率进行评价。但由于实际过程中存在数据非高斯性以及非线性的影响，使得该方法仅适用于线性或非线性较弱的对象［13］。

考虑到动态方法的有效性与ICA的非高斯性和高阶统计特征，使用动态独立元分析 (DynamicIndependent Component Analysis，DICA)进行故障检测在理论上具备更高的优越性，且在造纸废水领域对于DICA的运用尚未见报道。结合废水处理过程的非线性、非高斯性及动态特性，本实验通过引入时滞变量l，构建增广矩阵，分别通过构建DICA与DPCA方法对废水数据进行了故障检测与对比分析。

1 方法原理

1.1 PCA及ICA基本原理

1.1.1 PCA基本原理

PCA将空间划分为主元子空间以及残差子空间，并通过统计量是否超过控制线来对工业生产过程进行故障检测［14］。PCA主要用来将数据投影到更低维的空间来解决一些线性相关且符合高斯分布的问题。

将X∈Rn×m定义为n个样本和m个变量，将矩阵X分解如下:

式中，P^∈Rm×k为负载矩阵;T^∈Rn×k为得分矩阵;E为残差矩阵。

其中，得分矩阵T^∈Rn×k中的得分向量t如公式(2)所示;x的预测值x^如公式 (3)所示;残差向量e如公式 (4)所示。

T2统计量［15］给出了PCA模型中统计量的上限，如公式 (5)所示。

式中，n 为样本数;a 为主元个数;Fa，n－a，α表示在置信区间α下自由度为a和n－a的F分布。

1.1.2 ICA基本原理

ICA是一种将数据矩阵X分解成为统计独立分量线性组合的统计方法，其基本思想是提取驱动过程的基本独立组件，并将其与过程监控技术相结合［16］，使用 I2、I2e和SPE图进行在线监测，并对结果进行分析。

假设观测数据矩阵X∈Rm×n，其中m为样本数，n为变量数，通过ICA对X进行分解，得到公式(6)［7］。

式中，A∈Rm×r为混合矩阵;S∈Rr×n为独立成分矩阵;E∈Rm×n为残差矩阵;r为所选取的独立成分的个数。

1.2 DPCA及DICA基本原理

传统PCA在过程监测中只是关注某一时刻的观测数据，以观测对象各个时刻的状态处于静止作为前提，因此在生产过程较为稳定的工况下更为有效。然而实际工业生产过程大多数都存在动态特性，导致变量偏离稳定状态且不同测量变量之间存在着序列相关性［17］，这种变量之间的相互影响体现在不同时刻中，因此PCA方法在动态过程检测的有效性会大大下降。针对变量所存在的动态特征，需要考虑数据序列相关性及变量的延迟，为了解决该过程中的动态问题，采用了时滞转变的方法，引入时间滞后变量l来进行动态方法的构建。

1.2.1 DPCA基本原理

首先，DPCA运用于故障检测时，对原始数据矩阵进行增广［18］如公式 (7) 所示。

式中，X(l)是时滞数据矩阵;t是样本时间;n是样本数，x为矩阵X中的观测向量。

其次，DPCA在故障检测中对异常数据发出报警信号，通过得分矩阵及残差矩阵构建统计量T2和SPE［19］，其定义分别如下。

T2统计量定义为得分向量平方和，通过主元模型内部主元向量模的波动来反映过程中数据的变化，其定义如公式 (8)所示。

式中，t为得分矩阵中的得分向量;Λ为数据协方差矩阵特征值的对角矩阵。

SPE统计量又称Q统计量，定义为采样值与估计值残差的平方和，反映了某时刻测量值对主元模型的偏离程度，其定义如公式 (9)所示。

T2和SPE统计量的控制线是实际工业生产过程下的临界值，当测量值超过临界值时，则表明有故障发生，系统会将其认定为故障。T2统计量控制线如公式 (10)所示，SPE控制线如公式 (11)所示。

式中，Fk，n－k，α表示在置信区间 α 下自由度为 k和n－k的F分布。

1.2.2 DICA基本原理

DICA的故障检测，首先是进行增广矩阵的构造，其次是进行白化处理，利用FAST-ICA算法进行独立元的求解，最后计算统计量进行故障检测研究。

(1)增广矩阵的建立

DICA增广矩阵的构造与以上所提及DPCA相似，对其进行增广矩阵的建立如公式 (12)所示。

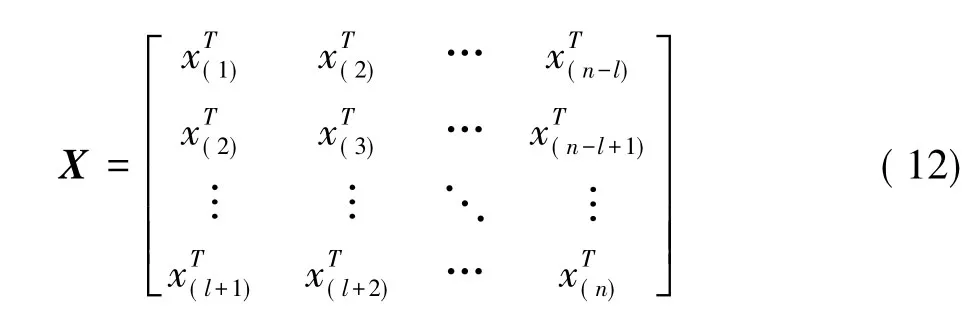
式中，n为采样点个数;l为滞后时间常数;x为矩阵X中的观测向量。

(2)白化处理

运用主元分析的方法进行白化处理，以此来消除过程变量之间的交叉相关性。

白化矩阵Q如公式 (13)所示。

式中，Λ为数据协方差矩阵特征值的对角矩阵;U为特征向量对应的矩阵。

白化处理后所得观测矩阵Z如公式 (14)所示。

式中，X为数据矩阵;S为独立成分矩阵。

(3)FAST-ICA算法

假设信号源相互独立，以源信号协方差矩阵及Z的协方差矩阵为单位阵如公式 (15)所示。

由公式 (15)可得B为正交矩阵。

由式 (14)得S的估计值S^如公式 (16)所示。

解混矩阵W可由公式 (17)所得。

(4)计算统计量

通过新观测数据采集得到实际测量变量的扩展向量xnew(k)以及动态独立成分的扩展过程变量解混矩阵W的行向量按估计值^s的行向量进行重排，选择主要部分组成Wd，解混矩阵W剩余部分则记为We，根据公式 (17)推导计算Bd，即:Bd=(WdQ－1)T

I2、SPE和I2e作为DICA统计量指标，计算公式分别如公式 (18)、(19) 和 (20) 所示［20］。

式中，k表示时间序列中的k时刻。

通过核密度估计方法分别对I2、I2e和SPE三种统计量的控制线进行计算，当测量值超出控制线即认定为发生故障。

2 结果与讨论

2.1 实验数据及变量选择

实验数据取自某废水处理厂，样本数据为2007年3月9日至2008年2月29日期间实际采集数据，共346组数据，9组变量。分别为进水流量 (Qin)、进水悬浮固形物 (SSin)、进水生物需氧量 (BODin)、进水化学需氧量 (CODin)、进水总氮 (TNin)、进水总磷 (TPin)、出水化学需氧量 (CODeff)、出水总氮(TNeff)、出水总磷 (TPeff)。

2.2 故障构建

废水处理过程的高度非线性以及外界系统干扰性，使废水处理过程具有较高的复杂性。本实验针对废水处理过程特点，构建了偏移故障、漂移故障及完全失效故障3种传感器故障，如图1所示。前246组数据为训练集，后100组数据为测试集，其中故障数据从测试集第31组数据开始加载。具体故障构建如表1所示，对进水化学需氧量CODin加入其均值的30%作为偏移故障，对出水总磷TPeff加入系数0.05来构建漂移故障，对进水总氮TNin的数据改为35作为完全失效故障。

表1 故障检测中故障构建公式

2.3 基于PCA及ICA的故障检测

2.3.1 基于PCA的故障检测

基于PCA对故障进行检测，主元数的选取为3。其中测试集中前30组数据为正常数据，后70组数据为异常数据，当前30组数据中有超过控制线的部分，则被认定为误检;后70组数据超出控制线则被认定为故障。实验结果如表2、表3所示，分别表示PCA故障检测率和PCA故障误检率。从表2和表3可知，在SPE统计量下偏移故障和完全失效故障的故障检测率均未超过36%且误检率均高达20%，漂移故障检测率虽然相对其他两种故障检测率较高，但SPE指标下的误检率也高达16.67%。从以上结果分析得出:基于PCA的故障检测方法对实际工业生产中的检测准确性较低且误检率较高。

表2 PCA故障检测率 %

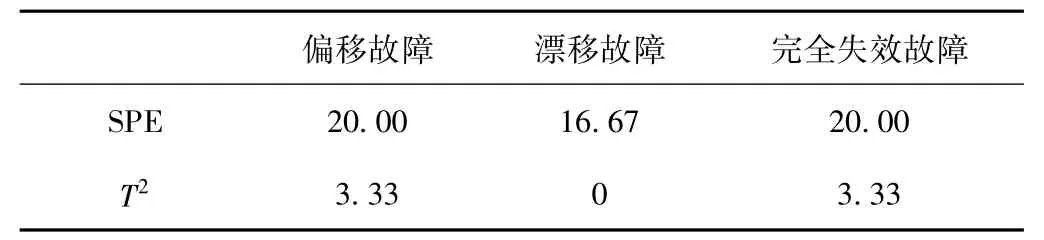
表3 PCA故障误检率 %

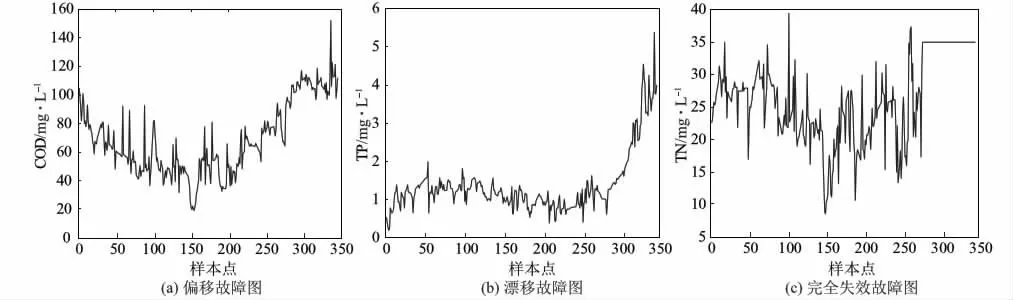
图1 3种传感器故障构建图

2.3.2 基于ICA的故障检测

基于ICA的故障检测与PCA方法相似，首先进行故障数据的加载，若测试数据超出控制线则被认定为故障，正常数据超出控制线则被认定为误检。实验结果如表4、表5所示，分别表示ICA故障检测率和ICA故障误检率。

通过表2、表4对比可以得出，基于ICA的故障检测率明显比PCA有了一定提升，在SPE统计量下相比于PCA分别提升了45.71%、4.28%及37.14%;误检率由基于PCA检测SPE统计量下的20.00%、16.67%及20.00%，在基于ICA检测I2e及SPE统计量下均下降为零误检。因此相较于PCA检测方法，ICA的故障检测效果优于PCA，尤其针对于PCA检测效果较差的偏移故障和完全失效故障有着较好的改善。这主要是因为PCA方法在过程中监测的变量并非相互独立的，PCA作为一种降维技术，通过将相关变量投影为一组不相关的变量，同时保留了原始方差的主要信息，以此减小数据维度，但不能使变量独立;而ICA可以从多变量数据中提取这些潜在成分得到更多信息，因此ICA可以较好地克服PCA方法依赖于数据满足线性条件的问题。当然ICA对于实际工业生产过程中存在的动态特性存在检测效果下降的问题，因此引入动态检测方法在实际工况中就十分必要。

表4 ICA故障检测率 %

表5 ICA故障误检率 %

2.4 基于DPCA的故障检测

通过以上对传统PCA检测结果分析可以得出，基于PCA的故障检测方法对于复杂工业生产过程的检测有较大的局限性，因此利用时间滞后转变来对数据矩阵进行拓展，从而克服工业生产过程中所带来的时变性问题，提高故障检测效果。本实验在使用DPCA方法故障检测过程中各主元特征值及其捕获方差如表6所示，故障检测率及误检率如表7、表8所示，选择的主元数为4。图2～图4分别为DPCA方法在3种传感器故障下的故障检测图，虚线为控制线。当样本点中的故障数据超出控制线即被认定为故障，正常数据超出控制线则被认定为误检。

从表2、表7中可以得出，在构建的3种传感器故障中，基于DPCA的故障检测率在SPE统计量下比PCA分别高出12.86%、7.14%和28.57%;在T2统计量下分别高出14.28%、14.28%和18.57%;从表3、表8中同样可以得到，基于DPCA的故障误检率在SPE统计量下比 PCA分别下降20.00%、23.33%和20.00%，在T2统计量下DPCA方法的故障误检率下降为零误检。

通过以上分析得出，DPCA故障检测率均高于PCA方法下的检测率，其原因在于DPCA考虑到了过程的动态特性，使该模型更适于实际工业过程中存在的动态特性，由此提高了故障检测率和误检率，一定程度上克服了工业生产过程所带来的动态特性。

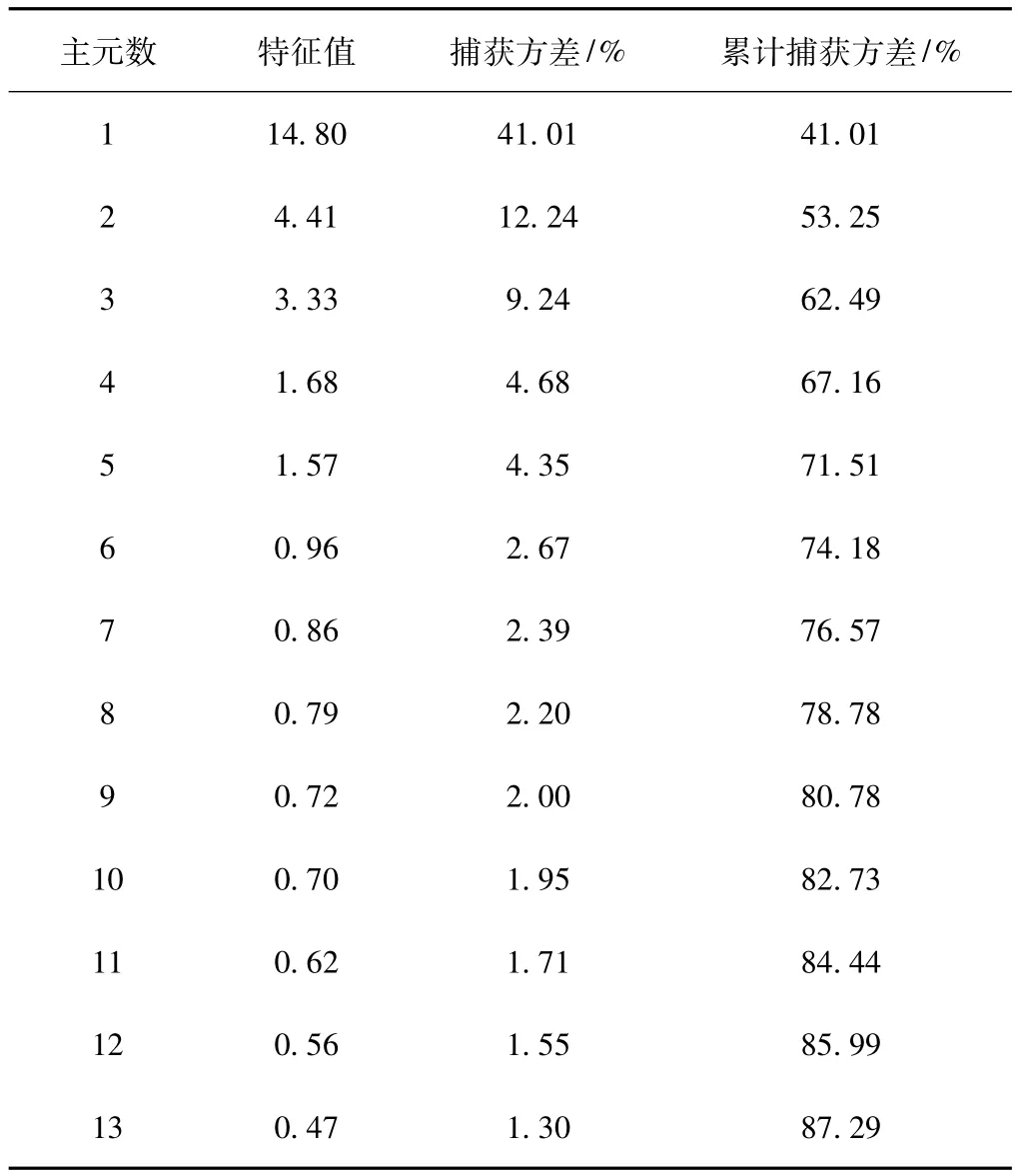
表6 DPCA主元个数及其对应特征值和捕获方差信息

图2 DPCA偏移故障检测图

图3 DPCA漂移故障检测图

图4 DPCA完全失效故障检测图

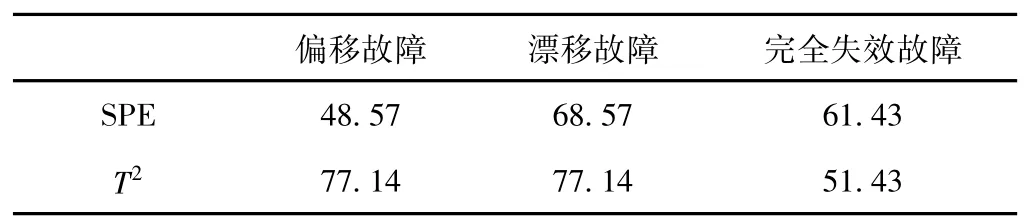
表7 DPCA故障检测率 %

表8 DPCA故障误检率 %

2.5 基于DICA的故障检测

通过以上对PCA、ICA以及DPCA故障检测对比分析可以得出，PCA对于处理线性特征的数据较为有效，但无法克服复杂工业生产过程中的非线性及动态特征问题，虽然对PCA引入了动态的DPCA方法，使得数据的动态特性有了一定的补偿，但仍然无法适应实际复杂工业生产中的过程检测，因此本实验引入DICA的方法。DICA方法是将ICA应用于具有时滞变量的增广矩阵，因为它能够提取独立于变量的自相关和互相关信息，在动态系统中可以从原始数据中提取独立成分，并通过引入时滞变量l来克服数据所具有的动态特征，提高了故障检测在实际生产中的准确性。DICA独立成分个数可由图5确定。DICA故障检测率及DICA误检率如表9、表10所示。

表9 DICA故障检测率 %

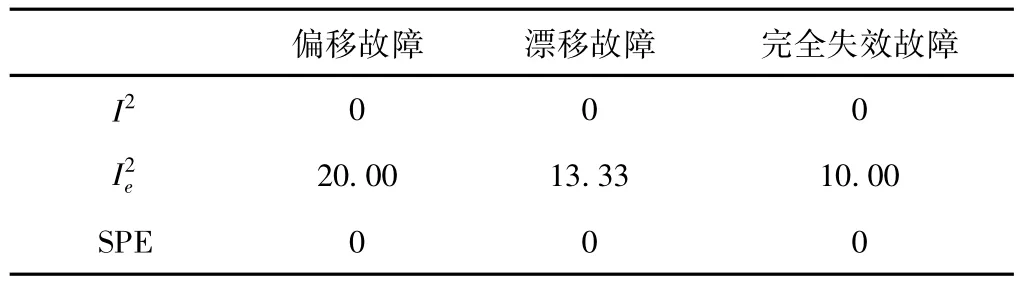
表10 DICA故障误检率 %

图6～图8为DICA方法分别在3种传感器故障下的故障检测图。通过表4和表9对比得出，DICA故障检测方法相较于ICA方法，其故障检测率在SPE统计量下分别提高了7.15%、18.58%及12.86%;在基于动态故障检测中，DICA的故障检测率在SPE统计量下相比于DPCA在3种传感器故障下分别提高了40.00%、15.72%及21.43%。由此可以得出，DICA方法对故障的检测效果均优于传统PCA方法及DPCA，尤其针对偏移故障，其故障检测率得到大幅提升。

其次，为进一步说明DICA对故障检测的有效性，还需从误检率角度进一步对比分析。从表10可以得出:DICA在I2及SPE指标下其误检率均为零，相比于传统方法及DPCA来说，使用DICA更加准确可靠，极大地降低了误检和误报的可能性。

图5 DICA独立成分个数

最后，通过DPCA与DICA的故障检测结果对比分析得出，DPCA较高的误检率主要源于实际工业过程中的数据普遍存在的非线性及非高斯分布，并且DPCA方法需要数据满足正态分布，依赖变量的二阶统计信息，因此对于存在非高斯特性的数据处理效果不佳;而DICA的潜变量相互独立，且DICA利用变量的高阶统计特征，同时可以克服过程动态特征所带来的问题，因此在复杂工业生产下DICA的检测效果优于DPCA。

图6 DICA偏移故障检测图

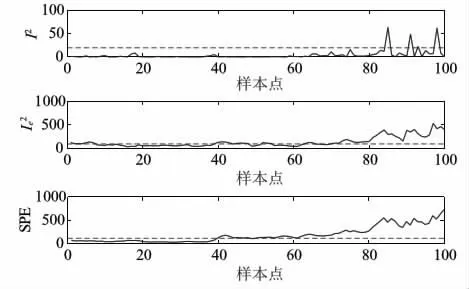
图7 DICA漂移故障检测图

图8 DICA完全失效故障检测图

3 结 论

本实验分别在废水处理监测过程中偏移故障、漂移故障及完全失效故障3种传感器故障下进行故障检测，结果如下。

3.1 相比于传统PCA，虽然DPCA的故障检测率在SPE统计量下分别提升了 12.86%、7.14%及28.57%，但DPCA存在较高的误检率，在SPE统计量下误检率均高达40.00%;相比于PCA，ICA对于故障检测率在SPE统计量下最高可提升37.41%。

3.2 DICA方法的故障检测率在SPE统计量下分别高达88.57%、84.29%和82.86%，且在SPE及I2统计量下均为零误检;相比于DPCA及ICA，DICA误检率最高分别下降了40.00%和10.00%。

3.3 DICA故障检测方法对于实际复杂工业生产过程具有更好的适应性，降低了数据的动态和非高斯分布特性对过程监测的影响，提高了工业生产过程的故障检测率并降低了误检率。