考虑短裂纹阶段的焊接结构疲劳寿命分析

魏国前，周东亮，胡 珂，党 章

( 1.武汉科技大学冶金装备及其控制教育部重点实验室，湖北 武汉，430081；2.武汉科技大学机械传动与制造工程湖北省重点实验室，湖北 武汉，430081)

常用的疲劳寿命预测方法有应力疲劳法、应变疲劳法和断裂力学法。前两种方法通过建立危险区域应力或应变参量S与循环次数N之间的关系，可以获得具有一定适应性的疲劳寿命值，但该值缺乏严格的寿命定义，无法对应具体的疲劳失效状态，在工程应用中受到很大限制[1]。断裂力学法以裂纹尖端的应力强度因子K作为主要控制参量，建立K与裂纹扩展速率(da/dN)之间的关系，求解初始裂纹扩展至临界尺寸或失稳断裂时所经历的循环次数。该方法具有较清晰的寿命定义，在结构设计尤其是焊接结构的疲劳寿命预测中获得广泛应用[2]。

应用于焊接结构的断裂力学法，其重要前提是假定焊缝区域普遍存在类裂纹初始缺陷。对此，不同文献提出了各自的类裂纹特征尺寸推荐值，一般在0.1～5 mm之间[3-4]，该取值范围较宽，给焊接结构的疲劳寿命预测带来极大的不确定性。Zhang等[5]对经过焊趾研磨处理的焊接接头试件进行研究，监测了裂纹萌生和扩展阶段，并分别采用Lawrence方法和Paris模型计算裂纹萌生寿命和扩展寿命，证实焊接质量较好时试件的裂纹萌生阶段占比较大。Ngoula等[6]采用J积分作为控制参量，研究了残余应力和焊趾形貌对裂纹扩展行为的影响规律，发现裂纹扩展初期行为和后期行为有较大差异。本课题组基于等效结构应力和99%下限主S-N曲线，针对焊接结构提出一种结合应力疲劳法和断裂力学法的疲劳寿命预测方法[7]。

上述研究都认识到焊接结构疲劳过程中裂纹萌生阶段的存在，但均没有探讨该阶段中裂纹的真实演变行为。实际上，将萌生裂纹的初始特征尺寸考虑为0.1～5 mm过于粗略，该尺寸区间涵盖了短裂纹和长裂纹初期这两种裂纹状态。已有研究表明，短裂纹对材料微观组织结构非常敏感[8]，一定条件下其可以在低于材料的裂纹扩展门槛值ΔKth时扩展[9]，扩展速率可能出现加速和减速等复杂行为[10]。为此，本文采用Kitagawa-Takahashi图方法，构造了考虑短裂纹阶段的裂纹扩展门槛值ΔKth与裂纹特征尺寸a的关系模型，并将其引入传统的Paris模型中，从而获得一种考虑短裂纹的疲劳寿命预测方法。然后利用该方法分析短裂纹阶段在结构整体疲劳寿命中的比重，并从微观晶粒尺寸的角度解释焊接结构疲劳寿命分散性较大的原因。

1 焊接结构初始缺陷

随着焊接技术的快速发展，重大装备和关键结构的焊接质量有了很大提升，焊缝初始缺陷的特征尺寸越来越小，有的甚至降至10 μm数量级。将焊缝初始缺陷视为初始裂纹是断裂力学的基本研究前提，不同尺度的初始裂纹对焊缝细微疲劳萌生和扩展行为的影响有很大差异。现有研究表明，常规意义上的裂纹萌生状态，即裂纹演变至可测量尺度，其界定在很大程度上依赖于裂纹检测手段和人为主观判断，该过程可能包含裂纹成核、微裂纹扩展、短裂纹扩展、长裂纹初期扩展等多个子阶段。因此，有必要按照尺度对焊缝初始缺陷进行细分，以便更准确地表征初始裂纹的特征状态。焊接结构的典型初始缺陷及其特征尺度如图1所示。

图1 焊接结构典型初始缺陷及其特征尺度

Fig.1Typicalinitialdefectsofweldedstructuresandtheircharacteristicscales

由图1可见，根据焊接结构初始缺陷的特征尺度的不同，可将其分成3个层次：

(1)对于焊接质量非常高的焊接结构，在焊接加工过程中没有引入额外的缺陷，但母材金属中可能存在初始夹杂物等，其尺度为1 μm数量级。特定条件下，这些夹杂物可能引发晶体内部的微裂纹，多数情况下，微裂纹主要在晶体内部活动，即使有扩展行为，往往也会在抵达晶界时受到强烈的阻碍作用，迫使其停滞在晶界处。只有在强大的外部驱动力作用下才可能重新激活微裂纹，促使其进一步扩展。因此，通常不将这一类缺陷视为裂纹。

(2)当焊缝材料在凝固过程中渗入气体，则可能导致孔洞、凹坑等缺陷。若这些缺陷位于近表面，且尺度、体积分数和聚集程度等达到一定阈值，将产生明显的局部应力集中效应，降低焊接结构的疲劳性能。这些焊缝初始缺陷的特征尺度多在10 μm或100 μm数量级，跨越少数几个晶粒的范围，其演变行为较大程度地受材料微观组织结构的影响，可将其视为“类短裂纹”初始缺陷。

(3)在表面熔渣和焊缝起止等位置，由于成形过程中温度急剧变化，容易形成肉眼可见的表面缺陷，尺度约在1 mm数量级。这些缺陷导致强烈的应力集中效应和复杂的残余应力分布，对焊接结构疲劳性能的影响非常大，可将其视为“类长裂纹”初始缺陷。

需要注意的是，短裂纹和长裂纹的扩展行为有很大差异，不能采用传统的Paris模型简单描述。因此，针对上述“类短裂纹”初始缺陷进行研究，应该采用考虑短、长裂纹两个阶段的扩展模型，并引入微观组织结构对短裂纹扩展行为的影响因素。

2 考虑短裂纹的寿命预测方法

2.1 短裂纹的扩展特性

Paris模型主要适用于长裂纹扩展行为的描述，应用于短裂纹则有较大的局限性。图2为传统Kitagawa-Takahashi图，可用来描述短裂纹状态下裂纹特征尺寸、应力范围和应力强度因子之间的关系。

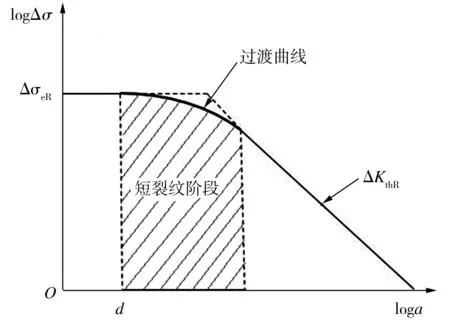
图2 Kitagawa-Takahashi图

根据疲劳理论，无缺陷材料存在疲劳极限ΔσeR，它是反映材料是否萌生裂纹的重要参数。同时，根据线弹性断裂力学(LEFM)理论，材料还存在长裂纹扩展门槛值ΔKthR，它是影响疲劳裂纹是否扩展的重要参数。Kitagawa-Takahashi图中，ΔσeR表现为一条水平直线，长裂纹扩展门槛值ΔKthR则表现为一条斜率为-1/2的直线。这两条直线之间的过渡曲线在物理意义上描绘了裂纹萌生和裂纹扩展的自然过渡，体现了短裂纹阶段的扩展行为。尤为重要的是，该过渡曲线表明，在短裂纹阶段，ΔKth不再是材料常数，而是与裂纹长度a有关的变化量。

晶粒内部微裂纹扩展至晶界时会遇到晶界阻力，这种晶界阻止微裂纹扩展的能力在宏观上即为疲劳极限ΔσeR。基于这一思想，可以构造短裂纹阶段裂纹扩展的微结构门槛值ΔKdR的表达式：

(1)

式中：d为晶粒尺寸。

将(ΔKthR-ΔKdR)定义为当裂纹闭合达到稳定水平时裂纹扩展门槛值的总外部分量，它是根据材料属性和裂纹长度而定的。首先建立裂纹扩展的总外部分量和裂纹长度a的函数关系，然后与材料的微结构门槛值ΔKdR结合，成为新的裂纹扩展门槛值求解公式，如式2所示[11]：

ΔKth=ΔKdR+(ΔKthR-ΔKdR)[1-e-K(a-d)]

(2)

式中：K为形状参数，求解方法如式(3)所示：

(3)

需要说明的是，当构件承受的名义应力等于材料疲劳极限时，一旦裂纹尖端的应力强度因子幅度达到上述微结构门槛值ΔKdR，裂纹将穿过晶界继续扩展，因此，ΔKdR可视为启动晶界处被阻滞微裂纹并促使其进一步扩展的最小值。

2.2 考虑短裂纹的裂纹扩展模型

(4)

式中：C和m为材料常数，可取与Paris模型相同的数值；ΔK为应力强度因子幅度，可采用下式计算：

(5)

式中：Δσ为应力值；Y为材料参数；MK为焊趾放大系数，详细求解可参照文献[13]。

3 模型验证

3.1 问题描述

为验证上述裂纹扩展模型，针对文献[14]中的L28型起重机走行梁试件的疲劳试验结果，采用不同方法进行疲劳寿命预测。文献[14]中的L28型试件梁采用与实际结构为1∶5的缩小模型，结构形式与关键尺寸如图3所示。该试件梁采用焊接工字钢形式，上翼缘板厚14 mm，下翼缘板厚11 mm，腹板厚度8 mm，上、下翼缘与腹板均采用双边角焊缝连接方式，焊脚尺寸8 mm。为便于工程安装，试件两端采用圆弧过渡方式，容易判断出圆弧过渡区域的焊趾为该结构梁的疲劳薄弱位置。

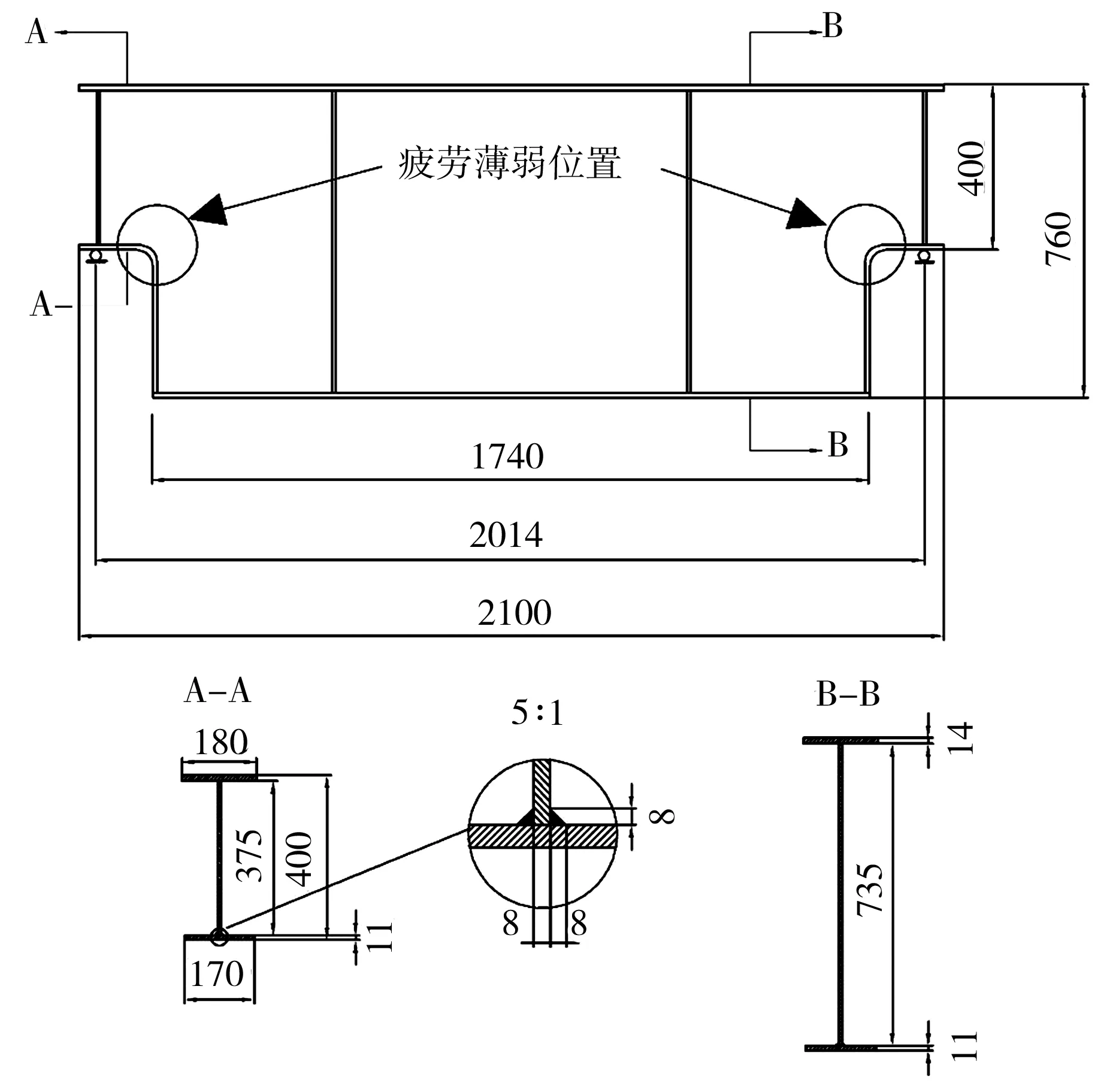
图3 试件梁的结构形式和关键尺寸

文献[14]针对5根L28型试件梁进行了疲劳试验，载荷形式为三点弯曲，载荷位置、大小和试验寿命如表1所示。试验结果表明，几乎所有试件梁两个端部的圆弧过渡区域都出现疲劳裂纹，裂纹表现为两种形态，一种沿焊缝扩展(1型)，另一种则在腹板上扩展(2型)，两种裂纹形态可能并存，但以2型裂纹为主要形态。在文献[14]中，试验寿命定义为对应裂纹长度为20 mm时的循环加载次数，针对同一个试件梁的2个端部，较早出现20 mm疲劳裂纹的试验寿命记录在括号外，另一端的试验寿命则记录在括号内。

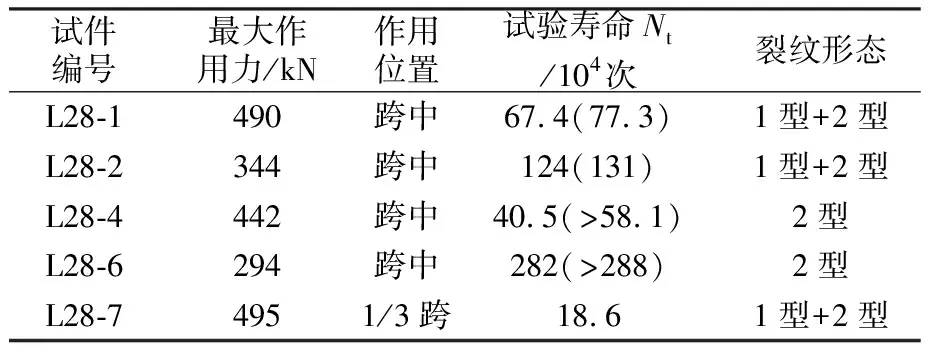
表1 试验工况

3.2 寿命预测

采用考虑短裂纹的裂纹扩展模型和传统的Paris模型计算试件梁的疲劳寿命，并与表1中的试验结果和文献[7]的计算结果进行对比。2个模型中，C=1.45×10-11，m=2.75[2]，ΔKthR=4.58 MPa·m1/2，ΔσeR=120.8 MPa，其余关键参数确定如下。

3.2.1 应力计算

采用有限元方法计算疲劳危险部位的应力。按照图3结构尺寸建立试件梁的有限元模型，按照表1中的试验工况确定载荷和边界条件。考虑到圆弧过渡区域的焊趾为重点关注部位，且存在显著的应力集中效应，故采用渐进过渡网格方式划分该区域的网格，如图4所示。焊缝区域共建有4层单元，靠近焊趾曲线的网格尺寸为2 mm，其他部分为10 mm。采用腹板侧焊趾处的最大主应力作为应力强度因子的计算参量，应力计算结果表明，最大主应力均出现在试件梁端部的圆弧过渡区域。对于L28-1、L28-2、L28-4、L28-6，由于载荷位于跨中，应力场对称分布；对于L28-7，由于载荷位于1/3跨度位置，最大应力出现在靠近载荷一端的圆弧过渡区域。最大主应力数值如表2所示。

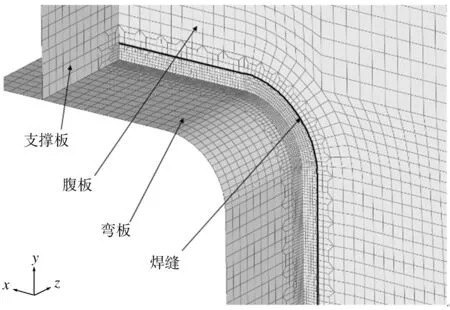
图4 过渡圆弧区域的有限元网格

Table2Calculatedvaluesofthemaximumprincipalstressinthefatiguevitalareas

试件编号L28-1L28-2L28-4L28-6L28-7应力/MPa201.5162.4232.4136.5305.2

3.2.2 裂纹特征尺寸的确定

利用断裂力学方法得到的是由初始裂纹扩展至最终裂纹所经历的循环次数，初始裂纹特征尺寸和最终裂纹特征尺寸对寿命预测有重要影响。焊接结构的焊趾裂纹多呈现为半椭圆表面裂纹形式，裂纹表面长度为椭圆长径2c，而裂纹沿板厚方向的深度为椭圆半短径a，本研究就是取半短径a为裂纹的主要特征尺寸。

短裂纹的尺寸多为晶粒尺度数量级，在萌生和扩展的前期，裂纹在焊缝区和热影响区，该区域内晶粒形态为针状结构，其晶粒尺寸和晶粒取向等都会对裂纹的扩展造成影响。为研究方便，本文在考虑短裂纹的裂纹扩展模型时，选用母材区晶粒尺寸作为初始裂纹特征尺寸ai。文献[14]中试件梁材料为Q345，平均晶粒尺寸d为0.028 mm，故取ai=0.028 mm。

文献[14]中的试验寿命对应的裂纹长度为20 mm，据文献[7]的研究，焊接结构的疲劳裂纹演变过程涵盖初始表面裂纹萌生、表面裂纹沿板厚方向扩展至贯穿裂纹、贯穿裂纹沿焊缝方向扩展至断裂等不同阶段，上述20 mm为断裂时的最终裂纹长度。而且实际上，一旦初始裂纹沿板厚方向扩展至板厚的一定比值φ，即可认为裂纹已贯穿板厚，之后的剩余寿命很短，可不予考虑。因此，为保证与文献[7]作对比分析时最终裂纹特征尺寸af的取值相同，本文也令比值φ=78%，并将所对应的裂纹深度值作为最终裂纹特征尺寸。由于试件梁的腹板厚度为8 mm，故最终取af=6.24 mm。

3.2.3 寿命预测结果

根据上述参数，采用式(1)～式(5)可计算试件梁的疲劳寿命，如表3所示，表中还列入了根据Paris模型的预测寿命和文献[7]中的计算寿命。需要说明的是，文献[7]中的计算寿命包含裂纹萌生和裂纹扩展两个阶段。

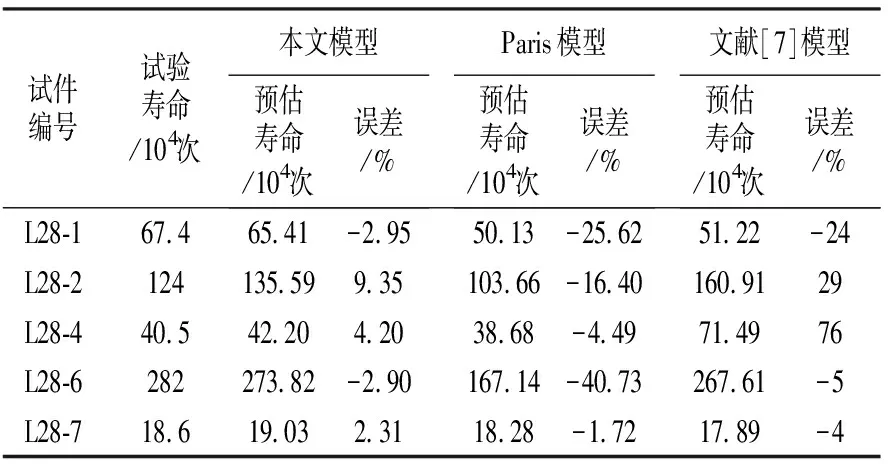
表3 试件梁的疲劳寿命预测结果

从表3可以看出，采用考虑短裂纹的疲劳寿命预测方法具有较高的精度和较小的误差分散性，最大误差仅为9.35%。Paris模型仅在L28-7试件上精度稍高于本文模型，其预测误差为-1.72%，而本文模型的预测误差为2.31%，两者均处于很低水平。文献[7]对几个试样的预测误差均高于本文模型。总体来说，本文模型优于另外两种方法。

3.3 寿命分析

3.3.1 寿命比值分析

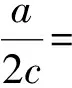
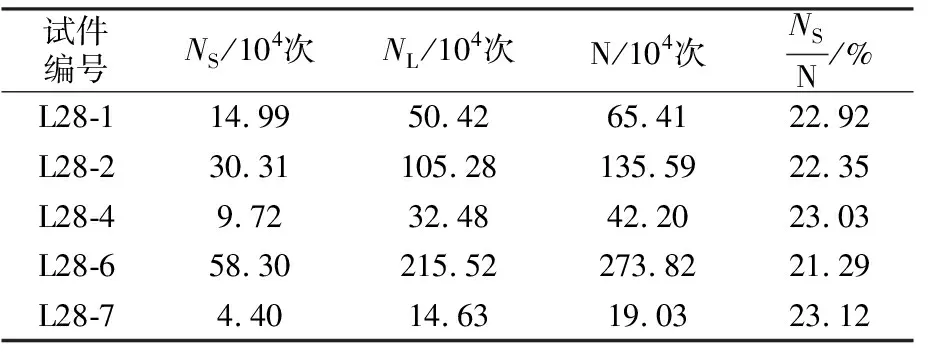
表4 短裂纹和长裂纹阶段的寿命比较

从表4可以看出，由于载荷状况不同，不同试件梁的各阶段寿命相差很大，但短裂纹寿命占总寿命的比值几乎都在22%左右，具有较好的一致性。这一方面表明短裂纹阶段在整个裂纹演变过程中占有不可忽略的比重，同时也表明将表面长度2c=0.25 mm作为短裂纹和长裂纹的分界点是合理的。

3.3.2 初始裂纹特征尺寸的反推

实际材料中微观晶粒尺寸是不同的，将初始裂纹特征尺寸取为固定值与实际情况并不相符。事实上，焊缝材料内晶粒结构的随机性在很大程度上导致焊接结构疲劳寿命尤其是裂纹萌生寿命的分散性。为此，针对表1中的试验寿命，将最终裂纹特征尺寸af固定为6.24 mm，利用本文模型，反推各个试件梁的初始裂纹特征尺寸ai，计算结果如表5所示。

表5初始裂纹特征尺寸的反推值

Table5Inversionvaluesoftheinitialcrackcharacteristicsize

试件编号L28-1L28-2L28-4L28-6L28-7ai/mm0.0220.0480.0370.0210.033

从表5可以看出，5根试件梁的初始裂纹特征尺寸均在晶粒尺度级，其数值在Q345材料的晶粒平均尺寸0.028 mm上下浮动，最大为0.048 mm，最小为0.021 mm。这些值可以简单理解为5根试件梁裂纹萌生部位的晶粒特征尺寸，表明焊缝焊趾附近区域的晶粒大小对焊接结构疲劳寿命有较大影响。

基于本文模型，以6.24 mm作为最终裂纹特征尺寸af，考虑不同的初始裂纹特征尺寸ai，获得不同晶粒尺寸(0.02、0.03、0.04、0.05 mm)对应的双对数S-N曲线，如图5实线所示。作为对比，针对图3试件梁的结构和载荷类型，考虑英国《钢结构疲劳设计与评估标准》(BS 7608:1993)中的C和D等级的S-N曲线，如图5中虚线所示。根据该标准，C和D等级均可用于非承载自动焊角焊缝接头，其中C等级对应于无焊缝起止等工艺缺陷，D等级对应于含有焊缝起止等工艺缺陷。从图5可以看出，面向不同晶粒尺寸的S-N曲线均在C和D等级的S-N曲线之间，且更加靠近C等级S-N曲线，这表明本文模型的预测寿命与相关标准在宏观层面具有一致性，同时也表明文献[14]中的试件梁焊接质量较高。另外，晶粒尺寸越小时，所对应的S-N曲线越靠近C等级的S-N曲线，也表明细化焊趾区域的晶粒尺寸可以提高焊接结构的疲劳性能。

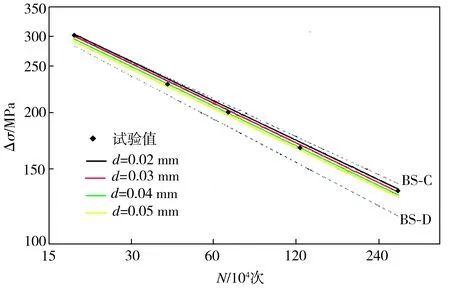
图5 不同晶粒尺寸对应的S -N曲线

4 结语

本文重点分析了焊接结构短裂纹的扩展特性，引入与裂纹特征尺寸a有关的裂纹扩展门槛值ΔKth，提出一种综合考虑短裂纹和长裂纹的裂纹扩展模型。通过与其他文献中的研究结果进行对比分析，验证了该模型的有效性和合理性。

然后，采用该模型计算短裂纹寿命占焊接结构疲劳总寿命的比值，分析了短裂纹阶段在焊接结构疲劳寿命预测中的重要性，并提出可以将0.25 mm作为短裂纹和长裂纹的分界点。

同时，基于该模型，将裂纹萌生处的晶粒尺寸作为初始裂纹特征尺寸，研究了晶粒大小对焊接结构疲劳寿命的影响，在一定程度上解释了焊接结构疲劳寿命值较为分散的原因。