基于PageRank与HITS的改进算法的网页排名优化
库 珊,刘 钊
(1. 武汉科技大学计算机科学与技术学院,湖北 武汉,430065;2. 武汉科技大学智能信息处理与实时工业系统湖北省重点实验室,湖北 武汉,430065)
PageRank算法是1998年由Google创始人Sergey Brin和Lawrence Page提出的基于链接分析的网页排序算法[1],其思想是通过分析网络的链接结构来获得网络中网页的重要性排名。传统的PageRank算法中,对于同一网页链出时的页面等级值(PageRank)是同等对待且平均分配的,没有考虑到不同链接的重要性会有所不同,而这与Web链接的实际情况不符。几乎在同一时期,康奈尔大学的Kleinberg博士提出了HITS算法[2],作为同样基于链接分析的算法,该算法中引入了枢纽(Hub)页面和权威(Authority)页面的概念,两者的相互优化关系构成了HITS算法的基础,但是两者在迭代过程中会相互增强,对查询结果的准确性造成影响。此后,相继出现了ARC[3]、SALSA[4]算法等一系列以链接分析为基础的页面分级算法,并且在实际应用中取得了一定的成果。另一方面,为解决传统PageRank和HITS算法中存在的不足,国内外研究者也提出了许多改进算法,如文献[5]提出了结合链接和内容信息的改进PageRank算法,其去除了PageRank算法需要的前提,考虑到了用户从一个网页直接跳转到非直接相邻但内容相关的另外一个网页的情况。文献[6]提出了通过在PageRank算法中添加链入链出权重因子、用户反馈因子、主题相关因子和时间因子,使得搜索结果更接近用户查询需求,同时兼顾了搜索内容的相关度和查准率。文献[7]提出利用PageRank算法对Lucene原有的排序算法进行改进,设计并实现了一个针对移动信息的个性化搜索引擎。文献[8]提出了一种结合网页文本分析和扩散速率改进的F-HITS算法,以解决传统HITS算法中易发生主题漂移、计算效率低等问题。
基于此,本文通过分析传统PageRank和HITS算法中存在的不足,提出了一种基于这两种算法的改进算法PHIA(PageRank and HITS Improved Algorithm),该算法继承了HITS算法获取根集和基本集的方法,并使用根集中所有网页的PageRank值作为Hub值和Authority值的初始迭代值,放弃了HITS算法中的相互迭代方式,而是通过求马尔可夫矩阵的方式来获取网页排名的静态分布。
1 网页排序算法
1.1 PageRank算法
PageRank算法是根据网页超链接之间的相互关系来确定网页的重要性和排名的,基于“由许多网页或一些权威网页链接的网页必然是权威网页”的前提条件,以网页间的链接结构为基础,来划分网页的重要性等级[9]。在链接网络中,将网页A指向网页B的链接看作是A对B的投票,根据一个网页所获得的投票次数来判断网页的重要性,一个网页的PageRank值PR可由下式(1)表示:
(1)
式中:i、j表示网页;Q(i)表示网页i指向的链接集合;S(j)表示网页j指向的所有链接的数目;PR(j)表示页面集Q(i)中任意一个页面j的PR值;PR(j)/S(j)则表示网页i的链入网页j给予网页i的PR值。
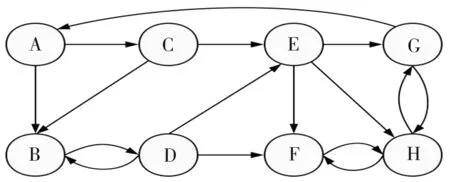
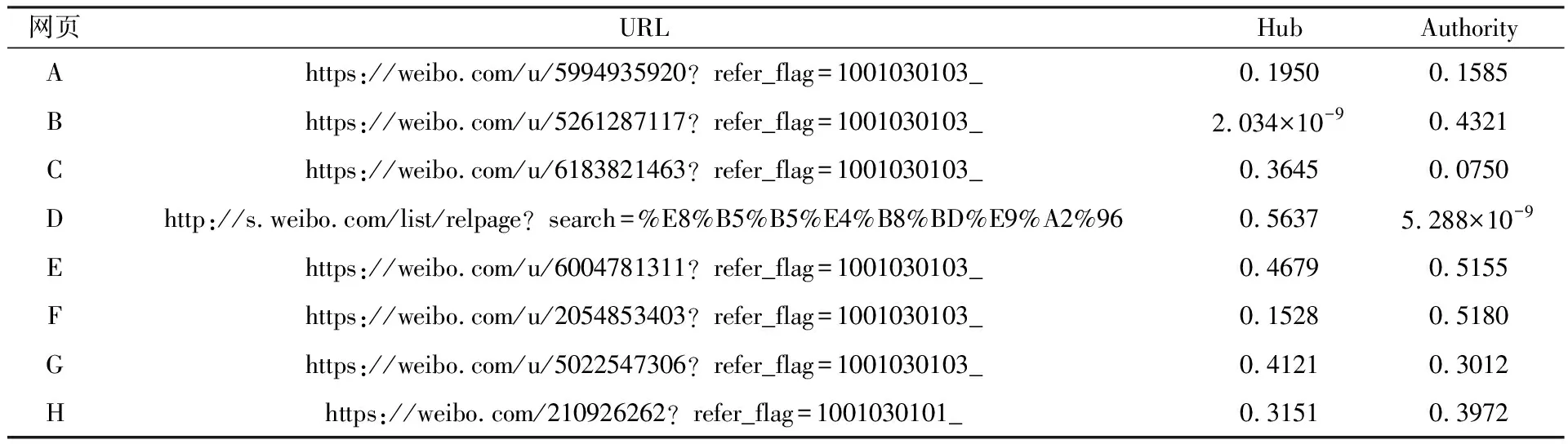
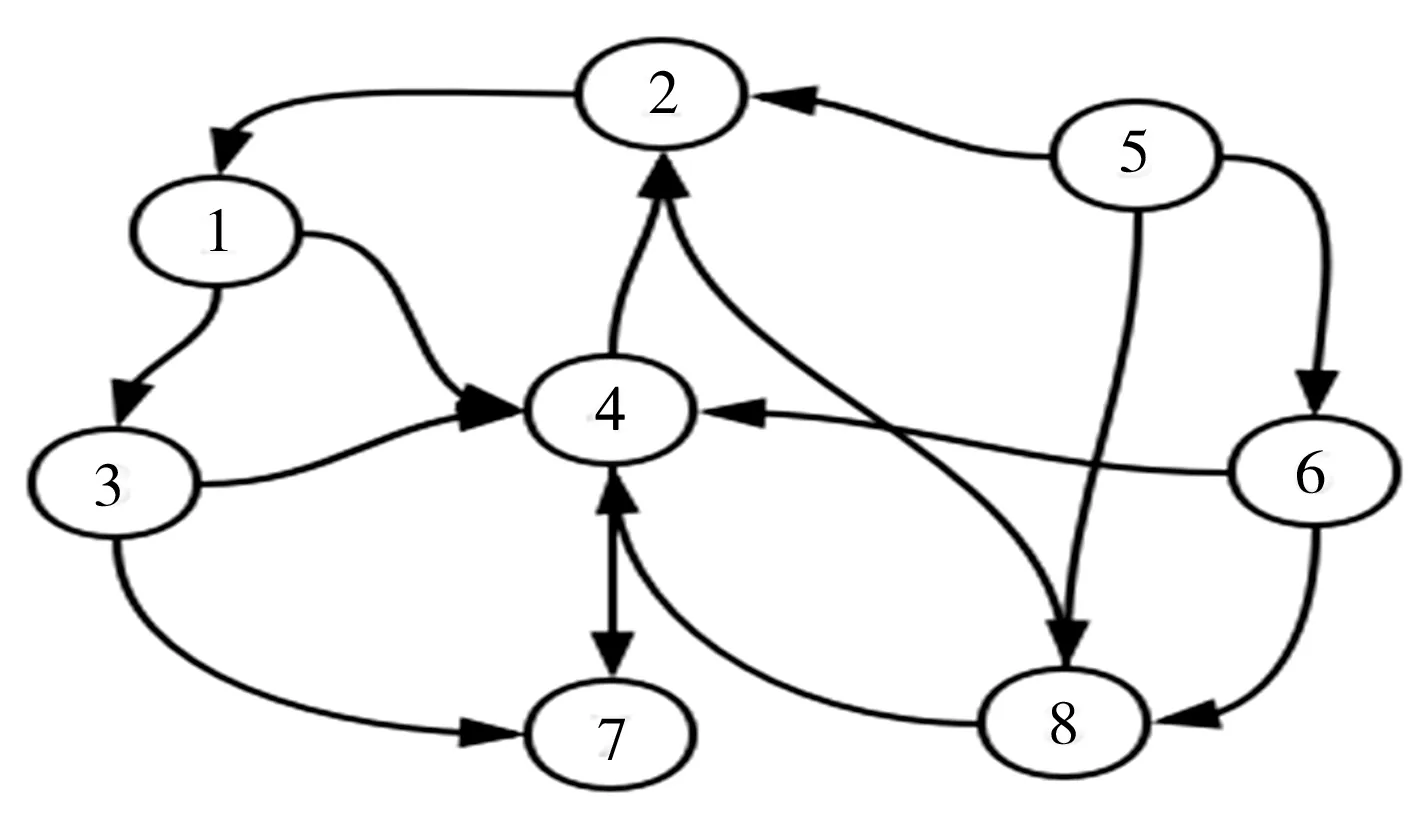
但在实际应用中,Web连接图中常常存在一些出度或入度为0的节点,即存在环的情况,这时会出现两种异常:等级泄露(Rank Leak)和等级下沉(Rank Sink)[10]。为避免上述现象,可以在去掉Web链接中所有出度为0的节点后,定义一个阻尼系数d(0 (2) 式中:m表示节点的总个数。 一个页面的PageRank值是由所有链向它的页面(链入页面)的重要性经过递归算法得到的,计算过程需要迭代。大量实验证明,经过反复迭代计算得到网页的PageRank值是收敛且有效的。PageRank 算法作为与查询主题无关的静态算法,所有网页的PageRank 值均可以通过后台离线计算获得,这有效地减少了在线查询时的计算量,降低了用户查询相应的时间。然而,PageRank算法的特点使其仍受制于主题漂移、偏重旧网页、忽视用户个性化等问题。 HITS算法是一种基于超链接分析的网页排序算法。该算法中,网页被分为Authority和Hub两种类型,所谓Authority页面指的是与查询主题最为相关并具有高质量、权威性的网页,Hub页面则是指提供指向Authority网页链接集合的网页。同时,也为每个网页定义了两个权值,即Authority值和Hub值,用来判断该网页对特定主题的重要性。 HITS算法的建立基于以下两点假设:①一个好的Authority页面会被很多好的Hub页面指向;②一个好的Hub页面会指向很多好的Authority页面。该算法的具体实现过程为: Step1将查询主题q提交给某搜索引擎,从返回结果页面的集合中取前n个结果作为根集Q,Q需要满足:①Q中网页数量足够小;②Q中包含很多与查询相关的页面;③Q中包含很多高质量的Authority页面。 Step2通过向Q中加入被Q引用的网页和引用Q的网页,将其扩展成一个更大的集合T。以T中的Hub 网页为顶点集V1,以Authority网页为顶点集V2,以V1到V2的超链接为边集E,形成一个二分有向图G=(V1,V2,E)。对于V1中任一顶点v,用h(v)表示其Hub值;对于V2中任一顶点u,用a(u)表示其Authority值。 Step3初始化a、h,令a0=h0= 1。 Step4分别对u、v进行如下操作,以修改a(u)和h(v)的值: ①a(u)=∑h(v);②h(v)=∑a(u)。 Step5对a(u)、h(v)进行规范化处理,即: Step6不断地重复Step4和Step5,直至a(u)、h(v)收敛,输出最大的Authority值和Hub值。 与PageRank算法不同,HITS算法与用户输入的查询请求密切相关,因而必须在接收到用户查询后进行实时计算,计算效率较低;另一方面,尽管HITS算法在某些查询主题下能够较为准确地提取出Authority网页,但若扩展网页集合里包含部分与查询主题无关的页面,且这些页面之间有较多的相互链接指向,那么使用HITS算法很可能会给予这些无关网页很高的排名,导致搜索结果发生“主题漂移”。此外,HITS算法还存在易被作弊者操纵结果、结构不稳定等问题。 针对上述不足,本文提出了一种基于PageRank和HITS算法的改进算法PHIA。该算法继承了HITS算法获取根集和基本集的方法,并且使用根集中所有网页的PageRank值作为Hub值和Authority值的初始迭代值,以避免“主题漂移”现象的发生;其次,改进算法放弃了HITS算法中的Hub值和Authority值相互迭代方式,而是通过求马尔可夫矩阵及其特征向量的方式来获取网页排名的静态分布,以避免其相互迭代所产生的增强值误差。算法PHIA的具体实现步骤为: Step1根据用户请求,用Google、Firefox等常用搜索引擎进行查询,取返回页面中的前n个网页作为算法的根集,记为Q。随后对集合Q进行扩充,方法为将根集Q中每一节点的入链(所有指向该节点的页面)和出链(该节点指向的所有网页)补充进来,形成基本集,记为SQ。 Step2求SQ中页面的PageRank值。设W为SQ中页面的集合,N=|W|,Ri为页面i指向的所有页面的集合,Bi为指向i的所有页面的集合;对每个出度为0或出度页面不在SQ中的页面s,设RS={SQ中所有页面的集合},则所有其他节点的Bi={Bi∪s},这样可以将结点s所具有的PageRank值均匀地传递给其他所有页面i。由此,页面i的PageRank值PR(i)可以通过以下两步计算得出:①以概率“1—m”随机取基本集SQ中任意页面i;②以概率m随机取指向当前页面i的页面j,如果j∉SQ,则重新选择页面j。PageRank算法的具体迭代公式为: (3) 式中:参数m为取值范围在0~1范围的衰减因子,通常被置为0.85。 Step3用计算得到的PageRank值代替SQ集中每一个页面的Authority和Hub初始值。从集合SQ构造无向图G′ = (Vh,Va,E),得到两条链,即Authority链和Hub链: Vh=(sh|s∈SQ∪出度(s)>0} (G′的Hub边) Va={sa|s∈SQ∪入度(s)>0} (G′的Authority边) E={(sh,ra)}s→rinSQ} Step4根据2条马尔可夫链[11]定义其变化矩阵,也即随机矩阵,分别是Hub矩阵H和Authority矩阵A。 (4) (5) Step5求出矩阵H、A的主特征向量,即为对应的马尔可夫链的静态分布,H、A中较大数值所对应的网页为所查找的重要网页。 为验证改进PHIA算法的正确性和有效性,本文建立了一个实验系统,即用网络爬虫工具Heritrix在Google搜索引擎上,采用BroadScope模式对新浪微博网站的“娱乐版块”和“研究版块”进行网页抓取。这两个板块中,各节点之间具有良好的互动关系,因此能够较好地模拟互联网的网络结构。本文随机选取“赵丽颖”和“Web前端”作为查询主题,由于本实验选择的新浪微博中两个板块的网页是由人工分类所形成的,并且所查询关键字的含义较为简单,故根据改进算法得到的每个网页的Hub值和Authority值是可以信赖的。 从以“赵丽颖”为主题查询得到的页面中选取前8 个页面,分别用A~H表示,各页面之间的链接关系如图1所示。利用PageRank、HITS及改进PHIA算法计算各网页的权值,结果列于表1~表3中。从表1和表2中可以看出,所选择的 图1 以“赵丽颖”为搜索主题的页面链接关系 Fig.1Pagelinkrelationshipwith“ZhaoLiying”asthesearchtopic 表1 以“赵丽颖”为搜索主题的基于PageRank算法的计算结果(迭代次数:15次) 表2 以“赵丽颖”为搜索主题的基于HITS算法的计算结果(迭代次数:20次) 表3 以“赵丽颖”为搜索主题的基于PHIA算法的计算结果(迭代次数:10次) 8个网页中,PageRank值最高的页面是H页面,其次为F页面和G页面;最好的Authority页面为F页面和E页面,最好的Hub页面为D页面,其次为E页面和G页面,同时有较高的Authority权值和Hub权值的页面为E页面、G页面和H页面。由表3所示改进PHIA算法的计算结果可知,具有高Authority值的页面为H页面、F页面和B页面,有高Hub值的页面为E页面、D页面和H页面,同时具有高Authority值和Hub值的页面为H页面、E页面和G页面。 以“Web前端”为搜索主题进行查询,从返回结果网页中选取8个页面,分别标号为1~8,其链接关系如图2所示,3种算法计算得到各网页的权值列于表4中。由表4可见,利用PageRank算法计算得到排序第一的是页面4,其次为页面1 和网页7;HITS算法下,最好的Hub网页为页面8,次为页面5和页面6,最好的Authority页面为页面4,其次为页面2;而改进PHIA算法下,计算得到Hub值较高的页面依次为页面5、页面8和页面1,Authority值较高的页面依次为页面4和页面2。 图2 以“Web前端”为搜索主题的页面链接关系 Fig.2Pagelinkrelationshipwith“Webfront-end”asthesearchtopic 根据上述实验结果可知,基于PageRank和HITS的改进算法PHIA能够更全面地找出所查询关键词的重要页面;更重要的是,PHIA算法所需要的迭代次数为10次,少于PageRank算法(15次)和HITS算法(20次)所需的迭代次数,计算量大大减少;根据对查询结果进行分析可知,页面H和页面E在内容上与搜索主题“赵丽颖”关联密切,页面4的内容与“Web前端”的关联度也相对较高。另外,当限制最大迭代次数时,若迭代次数较少,PageRank算法得到的高PR值页面是随机出现的,即可能是8个页面中的任一页面;HITS算法一直指向的是同一个页面,与迭代次数无关;PHIA算法则能够找到最好的Authority页面和Hub页面。可见,PHIA算法的精度要高于PageRank和HITS算法,不足之处是当迭代次数足够多时,HITS算法和PHIA算法精确度相差不大。 本文通过分析经典的基于链接分析排序算法PageRank和HITS中存在的不足,提出了一种改进算法PHIA。该算法继承了HITS算法获取根集和基本集的方式,并利用根集中各网页的PageRank值作为Hub值和Authority值的初始迭代值,在一定程度上避免了“主题漂移”现象的发生;另外,PHIA算法放弃了HITS算法中Hub值和Authority值相互迭代的方式,而是通过求马尔可夫矩阵来获取网页排名的静态分布,以解决两权值相互迭代过程中产生的增强值误差。从针对两个随机关键词的检索结果来看,PHIA算法虽然在一定程度上削弱了主题漂移和Hub值和Authority值相互迭代导致的增强效果,并且收敛速度也有了一定的提高,但是PHIA算法仍然存在一些缺陷,有待进一步改进:① PHIA算法只是在一定程度上削弱了“主题漂移”现象的产生,并不能完全避免;② 目前本系统只在本机中实验,未考虑到人机交互、并发等问题,故还需在实际应用中加以完善。1.2 HITS算法
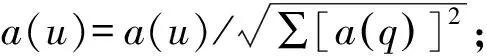
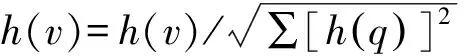
2 基于PageRank和HITS的改进算法PHIA
3 实验结果及验证


4 结语

