Mg-Al合金熔体中固液界面结构的分子动力学研究

熊 朝， 李 克， 周耐根

(南昌大学机电工程学院，南昌330031)

1 引 言

通常我们对晶体的生长、固化等现象的认识，来源于对固液界面的研究[1-3]. 但传统的实验方法，由于实验条件的限制，很难获得固液界面的主要特征，如界面处的原子结构序、化学序等[4,5]. 尽管近年来X射线衍射技术和高倍电子显微镜的发展，能使人们观测到实际固液界面，并证实了一些信息，如界面方向的密度有序、二维有序等[4,6-8]，但显然还不够. 因此，分子动力学模拟正成为研究人员研究固液界面的首选方法，并且对于界面结构特征的研究成果也大多来自于分子动力学方法.

固液界面比较重要的一个特征就是在界面附近有多个序参量会发生变化，并间接影响液体结构. 很多研究人员对金属熔体凝固过程进行了研究[9-12]，或者研究其团簇结构[13-15]，而对于固液界面的研究相对较少，且大多研究的是单一金属[16-20]或者纯物质[21]的固液界面，对于二元合金的固液界面，则研究较少[22]. 金属镁及其合金由于其优良的性能在材料研究中得到了重要应用，其中Mg-Al系合金是最常用的典型镁合金. 在镁合金零件铸造成型的凝固过程中均存在固液共存状态和固液界面，对镁合金凝固过程中的固液界面结构与特性进行研究，有助于增进我们对Mg-Al合金多相凝固组织形成、溶质成分分布、合金相形貌、微观偏析等现象本质的理解. 本文采用分子动力学方法对Mg-3%Al合金熔体中固液界面结构进行模拟研究. 为了研究固液界面法向方向的结构变化，计算了数密度沿界面垂直方向的分布以及晶体原子数在界面垂直方向上的分布情况；通过分析界面附近的径向分布函数研究界面的原子层结构，同时通过分析界面处原子的均方位移和原子扩散系数，探索界面处原子的扩散行为.

2 模型与方法

2.1 模型构造

首先以Mg在常温下的晶格常数构建Mg的晶胞，随后按3%的比例，将Al原子随机替换掉Mg原子. 然后参考郑小青论文中的方法[22]，计算得到该体系的固液共存温度，约为761K. 采用Liu等1997年提出的EAM势[23]来描述金属Mg、Al原子间的相互作用.

之后根据固液共存温度下纯Mg的晶格常数构造了Mg-3%Al合金的块体. 体系共有12000个原子，取密排面Mg(0001)构建固液界面，取垂直于(0001)面为z轴，沿z轴方向固定其中一半原子. 接着升温使另一半原子熔化，使固相和液相各有6000个原子. 最后，整个体系的温度降至761 K，获得如图1所示的固液界面模型. 运算过程中，时间步长为0.001 ps，体系的三个方向均为周期性边界条件. 图中，橙色代表Mg原子，绿色为Al原子.

图1 Mg-3%Al固液界面模型Fig.1 Solid-liquid interface model of Mg-3%Al alloy

2.2 微观结构的表征

2.2.1 数密度分布

数密度分布对于分析固液界面处法向有序具有重要意义[24-27]. 为了计算数密度分布，我们将整个体系沿z轴划分若干个区域，每层间距为层间距的1/10，计算每个区域内的Mg原子数、Al原子数及总的数密度. 数密度分布定义为：

(1)

2.2.2 均方位移(MSD)

均方位移是指粒子位移平方的平均值，其定义如下：

(2)

其中，ri(t0)代表原子i在零时刻的位移，ri(t)表示原子i在t时刻的位移；<>表示MD平均. 根据爱因斯坦扩散定律，均方位移可以用来表征液态金属原子的扩散行为. 扩散系数则可由原子的均方位移(MSD)随时间的变化斜率得到，即

(3)

2.2.3 晶体原子数

为了区分固液相原子，我们引入晶体原子数[28,29](Nc)这一概念，通过晶体原子数在z轴的分布情况，了解固液界面的有序情况. 其计算方法是，以某一原子为中心，以当前温度下的第一近邻与第二近邻距离的平均值为半径画球，看球内原子数是否等于完整晶体的第一近邻数. 如果相等，则称其为晶体原子；反之则为熔体原子.

2.2.4 径向分布函数(RDF)

径向分布函数g(r)表示为在半径r处厚度δr的球壳内，找到另一个原子的概率，是一个量纲为1的量. 要计算g(r)，我们先求出球壳体积V：

(4)

如果在这个球壳内的粒子数为n(r)，单位体积内的粒子数是ρ，则可得[30]：

(5)

3 结果与讨论

3.1 数密度分布

图2分别是Al、Mg和总精细数密度沿界面法向方向的分布图，以及数密度分布对照图. 每个数密度分布都截取了四个时间段，分别为初始0时刻、300ps、600ps和1000ps. 由图可知，无论是Mg、Al，还是总的数密度分布，在固体区域呈现出规则的周期震荡，在液相区域，密度分布更为无序. 同时还可以观察到，初始时刻，Mg原子的数密度分布和总数密度分布，两边波峰都较高，然后向中间逐渐减小，到达液相区域时，数值就较为平滑. 这种情况可能是由于初始时刻原子尚未发生移动，基本都处在同一z轴值，所以峰高而窄. 而越靠近液相，原子的束缚就小得多，峰低且宽，见图2(d). 随着模拟的进行，固相区域的原子在自身位置发生微小的偏移，每层原子数趋于一致，呈现出规则的周期震荡，每个波峰数值也相差不大. 由图2(e)可以看出，Mg原子和总数密度分布整体看起来相差不大，可能是由于体系中Al原子的比例较小，只有3%，所以对总数密度分布影响不大，与Mg原子的数密度分布近似. 其中，1、2等数字代表的是界面处十个区域，即十个原子层.

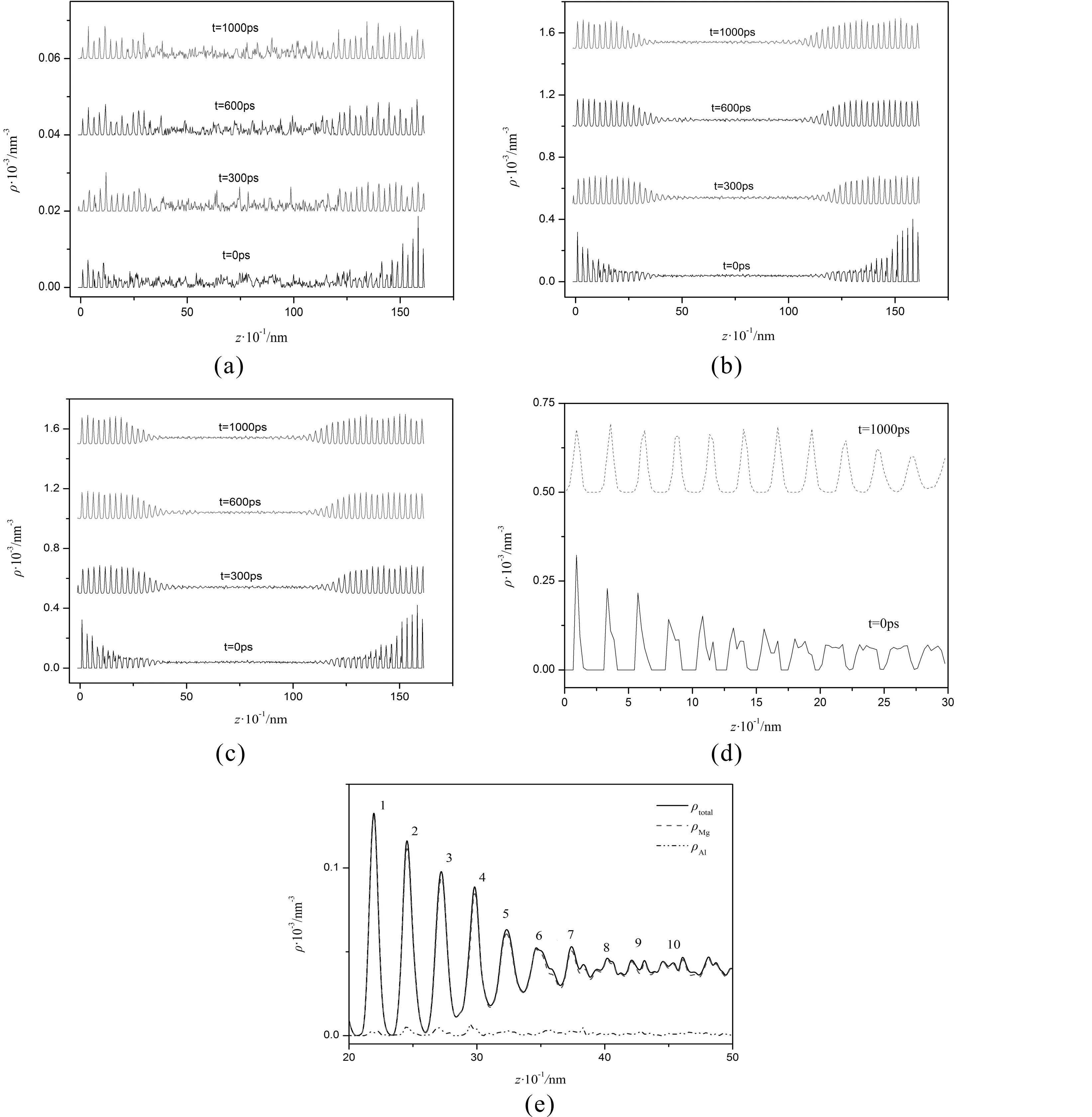
图2 (a)、(b)、(c)分别为Al、Mg、总数密度分布；(d)总数密度分布的不同时刻对比；(e)某一时刻Mg、Al和总数密度分布对比Fig.2 The number density distributions of (a)Al, (b)Mg and (c)in total; (d) The contrast of the total number density distribution at different times; (e)Comparison of Mg, Al and total number density distributions at a moment.

不过，我们也发现，Al原子的数密度分布相较于Mg原子来说，显得更为杂乱，虽然我们能清晰的看出固液两相，固相波峰波谷清晰明了，液相则无规律分布. 但是，即使在固相区域，Al原子的分布也并非较为规律，波峰不齐整，有高有低，甚至于在液相区域，数值有时也比固相大. 原因则可能是在构建固液体系时，因Al原子随机替换Mg原子，所以造成有些区域Al原子偏多，而有些区域Al原子偏少. 当其处于固相时，原子位移较小，所以导致固相区域Al原子分布有明显的波峰波谷，但数密度分布大小不一. 而处在液相区域的Al原子，在液相中各自扩散，则容易产生某处原子密度大，某处原子密度小的现象，也就造成液相中某些区域的数密度分布大于固相某些区域.

3.2 MSD与扩散系数

图3(a)所示为761 K温度下的MSD与时间关系图. 图中的1、2等数字代表的是固液界面附近的10个区域，其位置可参考图2(e). 由图可知，区域1和2均方位移很小，呈现出固相的特征；区域6、7、8、9、10的均方位移数值很大，为液相特征；区域3的均方位移相较于区域1、2来说较大，但整体说来数值仍然很小，基本呈现出固相的特征；区域4、5均方位移逐渐增大，但远小于区域6等区域，表明该区域的结构特征界于固相和液相之间.

根据各个区域的均方位移可求出不同区域的扩散系数. 图3(b)为选取的计算MSD的10个区域的总扩散系数，其中横坐标为距z轴原点的距离. 由图可知，区域1、2和3的扩散系数很小，几乎为零，表明这些层是完全有序的晶体结构；从区域4开始，扩散系数迅速增大，直到在区域6、7、8、9、10维持在3.3×10-9m2/s上下波动，表明该区域具有熔体结构特征；区域4、5则是固液相之间的过渡区域，越靠近液相，扩散系数越大.

图3(c)是各区域扩散系数三个分量Dx、Dy和Dz的变化规律. 由图可知，x、y和z三个方向的扩散系数在远离固液界面的固相内均趋近于零，反映了液体的对称性. 在固液界面附近，三个扩散分量存在明显的各向异性：Dz

图3 (a)不同区域的均方位移与时间关系; (b)对应的总扩散系数；(c)扩散系数D的三个分量Dx(正方形)、Dy(菱形)、Dz(三角形)Fig. 3 (a)Relation between mean square displacement and time of different areas and (b) corresponding total diffusion coefficient; (c) Three components of the diffusion coefficient D: Dx (Square), Dy (Diamond), Dz (triangle)

3.3 晶体原子数

图4所示为晶体原子数和总原子数(Ntotal)在z轴上的分布情况. 图中总原子数分布曲线与图2(e)中的总数密度分布曲线趋势是一致的，只是一个纵坐标代表的是数目，一个代表的是密度. 由图4可知，晶体原子数的分布情况与总原子数分布也相类似. 我们发现，在固液界面附近，晶体原子数会先于总原子数分布发生变化. 对比均方位移、扩散系数以及总数密度分布计算结果可见，区域4和5是固液两相过渡区域，区域6为液相，而晶体原子数却在区域3就开始变化，到区域5时就成为液相，晶体原子偏少. 这是因为处于液固界面附近的原子，固相一侧的原子分布排列有序，而液相一侧却排列无序，虽然是处在固相之中，却并非晶体原子.

同时我们也发现，晶体原子数总是小于总原子数，且液相区域也有若干晶体原子，这可能是固相区域的某些原子不满足判定条件，而液相区域有原子满足之前晶体原子的判定条件，所以才出现这种情况. 而固相处晶体原子较多，液相处晶体原子数普遍较少，也可让我们轻而易举的判断出固相液相.

图4 晶体原子数与总原子数在z轴上的分布情况Fig.4 Distribution of the crystal atoms number and total atoms number along axis Z

3.4 径向分布函数

二维径向函数分布具体计算方法与2.2.3一样，原子i与j之间的距离被定义为rij2=xij2+yij2，最后对整层原子求平均得到.

在固液界面附近选取五个区域a、b、c、d、e，即五层原子，对应前面计算MSD时的区域1、3、4、5、6，分别计算得到各区域的二维径向函数分布如图5所示.

由图可知，a层和b层的g(r)具有典型长程有序的特点，表明这两层具有较完整的晶体结构；c层和d层除了峰的高度不同外，其他与a、b两层相似，表明这两层仍然以长程有序为主，但同时也可以看到有序性的强度相较于a、b两层明显降低；e层除开始有几个波峰之外，之后趋于平缓，表现出短程有序、长程无序的特征，这显然是液相的显著特征. 这些层数的二维径向分布函数的结果与之前计算扩散系数的结果吻合.

图5 a、b、c、d、e等五层原子的径向分布函数Fig.5 The radial distribution functions of the a, b, c, d and e atomic layer

4 结 论

本文采用分子动力学方法系统研究了Mg-3%Al合金的固液界面结构和原子扩散行为，得出以下结论：

(1)Mg-Al合金中的液固界面是一个粗糙界面，即界面处原子呈现出高低不平，存在2～3个原子间距厚度的过渡层.

(2)垂直于界面方向的数密度分布，表现出复杂波动的特征，这种波动一直延伸到液体中；Mg原子的分布较于Al原子则更具规律性. 晶体原子数的分布规律与数密度分布趋于一致，但会先于数密度分布发生变化.

(3)界面附近三个方向的扩散系数分量表现出了明显的各向异性，并且这种向异性一直持续到液相当中.

(4)对界面二维结构的分析表明，在液固界面附近区域内，液相原子的二维排列呈现出从长程有序逐渐过渡到短程有序的变化.