快堆悬浮式非能动停堆组件移动体落棒性能分析

彭冠男，匡波，王欣，刘鹏飞，袁浩然

上海交通大学 机械与动力工程学院，上海 200240

钠冷快堆可采用悬浮式非能动停堆机构组件。作为冗余的多样的非能动停堆方式，在假想的 无 保 护 瞬 态 (anticipated transient without scram，ATWS)[1]条件下发生无保护失流 (unprotected loss of flow，ULOF)[2]事故时实施停堆，以提高快堆固有安全性。其中，这一停堆系统中最核心的部件——悬浮式非能动停堆机构组件[3](passive shutdown subassembly，PSS)在ULOF条件下的落棒水动力特性设计十分关键。本文通过对PSS的水动力分析与计算，探讨其各关键部件对动态落棒特性的影响，为PSS水力设计、优化及可靠性提供分析支持。

1 PSS 原理及移动体受力分析

如图1所示，正常工况下，PSS的移动体(内装中子吸收体)，在正常堆芯流量作用下悬浮于上位，浮力及水力推力之和大于移动体重力，依靠结构限位提供的向下机械推力使移动体悬停；发生ULOF时，堆芯流量大幅下降，其所受水力推力也随之下降，至某临界流量以下时，移动体所受合力发生变化，水力推力不足以抵消重力，移动体开始向下移动，直至底部下工作位[4]处，起到落棒停堆作用。

正常运行条件下，移动体悬停于上工作位，移动体受水力推力FDR、浮力Fb、自身重力FG及机械推力FM(仅在移动体处于上工作位时存在)，用以在上工作位时平衡其他各力产生的向上合力，使其停在上部限位处(上工作位)；在堆芯流量降至临界流量以下，移动体开始下落时，FM即转变为零。在悬停于上位时，上述各力代数和为0，移动体保持静止；发生ULOF时，堆芯流量开始下降，其值小于临界流量时，移动体下落，此时仅受水力推力FDR、浮力Fb、自身重力FG这3个力的影响，且FG>FDR+Fb，移动体所受合力向下，移动体开始自上向下移动。由于浮力Fb及自身重力FG在下落过程中保持不变，移动体所受合力大小主要取决于水力推力FDR。为保证移动体下落的可靠性，通过结构设计发现，移动体所受合力随下落位移的增大而增大，使得移动体在下工作位时具有液力自紧的特性；另外，为了防止移动体速度过大导致移动体运动至底部时与外套管发生猛烈撞击，在保证液力自紧特性的前提下需使移动体具备一定的缓冲效果。

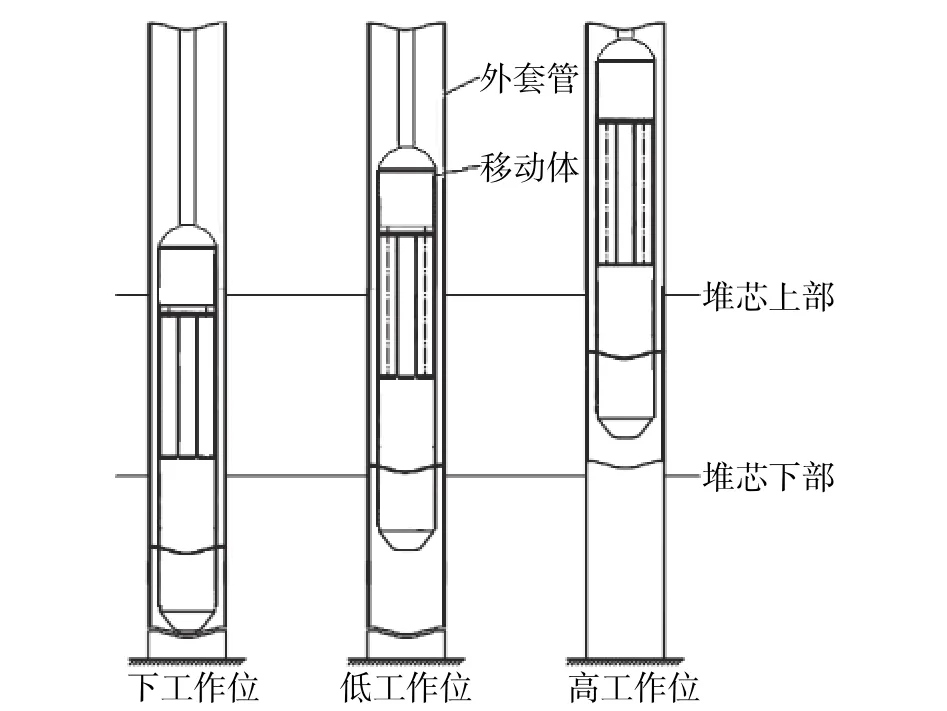
图1 PSS 原理

2 移动体运动模型及计算

移动体的运动计算主要基于移动体动力学及运动学方程：

式中：m为移动体质量，kg；a为该时刻下移动体加速度，m/s2；t为所选时间步长，s；u0为该时刻初的速度，m/s；x为移动体位移，m，向下取正。

式(1)模型方程中，浮力Fb及移动体重力FG在悬停与落棒过程中保持不变；而移动体所受水力推力FDR则较复杂。它是冷却剂通过组件移动体及其与外套管之间形成的复杂流道结构时，移动体两端产生压降而形成的对移动体的推力作用。不同入口流量下，形成水力推力的压降取决于通过该复杂流道各分支的流量分配，在计算过程中本文基于流体网络(流网)理论求解该流量分配[5]，经相关的简化修正，得到移动体上下两端压差及水力推力，进而通过运动模型方程可求解移动体的运动。

移动体所受水力推力FDR取决于移动体及其与外套管之间形成流道结构上下两端的压差ΔP，则FDR可写为：

式中：Se为移动体等效截面，由移动体和外套管间切应力为0的面组成，m2；ΔP为移动体上下两端压差，Pa。显然，ΔP是随移动体位移x以及冷却剂流量Q变化的函数。在ULOF时，FDR随着移动体的下落以及组件入口流量的降低而发生变化。

本模型的建立基于各组件稳态条件下的压降计算模型[6]，结合运动条件做了相关修正，属于一种准稳态[7]的计算方法，适用于移动体速度不大的情况。在该情况下，对应于某一入口流量Q与某一位移x，移动体及其与外套管间形成的各子流道中流量依流道结构进行分配，进而形成移动体两端总压降ΔP、流量Q及其在各子流道结构中的流量Qi。由此而形成的压降ΔP可近似由流网方程控制。

考虑PSS组件流道质量守恒与压降平衡，运用流体网络的基尔霍夫定律(即各节点流量的代数和为0，节点间不同支路的压降相等)进行复杂流道结构内的流量分配与压降计算。

以图2所示的PSS流道结构建立的流道模型为例，其中移动体与外套管组成的流道结构由缓冲区 (0.62 m起始)(1→2)、尖头 (3→4)、移动体下节流孔(6→12)、吸收体棒(15→16)、移动体上节流孔(18→19)、移动体上出口腰型孔(20→10)、移动体−外套管间宽环缝(6→8)移动体−外套管间窄环缝(8→9)组成，流网的节点方程写为

式中：Q1~Q7为图2中对应流量，且Q1为已知的主流量，kg/s； ∆ pi−j−k为其下标对应路径的压降值，Pa。

此外，考虑到移动体与流体相对运动对上述各流量及压降的影响，需对PSS结构中流道各压降与流量进行运动修正。

对于移动体−外套管间环缝，移动体下落会使其外壁面与流体的相对速度增加，对此类流道可对压降Δp进行修正：

式中： δp为压降 Δp的修正值，Pa； fn(Qi)为流道n的沿程压降计算函数；u为 移动体速度，m/s； An为流道n的截面积，m2；Qi= ρ uAn为该结构流道中流体相应于移动体下落速度的流量，kg/s。

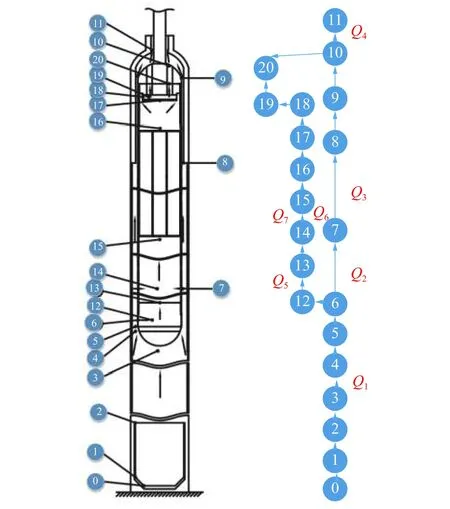
图2 流道网络

移动体与外套管间的突缩结构如图3所示。若突缩发生在移动体侧，移动体运动会造成流道体积损失。假设流体不可压缩，引入移动体下落排开流体的质量流量后，得到：

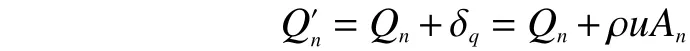
图3 移动体与外套管间突缩

3 计算流程

根据上述流网与压降计算，对于移动体运动模型，编制了PSSD程序，用以计算液体悬浮式非能动停堆组件移动体的落棒运动，以及落棒过程中PSS各处流量分配与分布压降等。程序的计算流程如图4所示。在移动体运动过程中，某些结构会发生改变，流道也随之变化，PSSD程序可自动进行流道重组，从而考虑PSS在不同位移x处的流道结构、相应的流量分配与分布压降，直至移动体达到下部限位(下工作位)。

图4 计算流程

4 移动体落棒性能计算

本文采用PSSD程序，对特定流道结构尺寸[8]的PSS(本文简称基准PSS)，结合给定的惰转流量曲线[9]，对移动体进行了其从上工作位至下工作位的落棒运动计算。然后，对基准PSS移动体部分流道结构尺寸进行了关键结构尺寸的参数敏感性计算分析，以期了解移动体结构尺寸对落棒运动的影响，为PSS移动体水力设计及其结构尺寸优化提供参考与支持。

4.1 时间步长的选择

在运用PSSD程序进行PSS移动体的落棒运动特性之前，需对计算进行时间步长敏感性分析。本文针对PSS基准结构分别采用Δt=0.5、0.1、0.01、0.001、0.000 5 s进行落棒计算，计算结果如图5所示。可以看到，只要时间步长Δt≤0.01 s，则所计算的落棒曲线就无明显差异。鉴于此，后续计算研究采用的时间步长Δt=0.001 s。

图5 不同时间步长下计算结果

4.2 基准结构尺寸移动体的落棒运动

采用如图6所示的惰转流量曲线，用以模拟ATWS可能发生的ULOF事故下的流量降低。

图6 入口流量曲线

通过基准PSS的落棒运动计算，得到基准移动体位移随时间的变化关系如图7所示。可以看到，移动体在 8.082 s、入口临界转变流量[10]为Q=1.99 kg/s时，开始自上工作点开始下落，在15.523 s达到下工作点，落棒时间为 7.441 s。

移动体下落曲线主要分为2段：1)移动体悬停阶段[11−12]；2)移动体下落阶段。在移动体悬停阶段中，所受水力推力FDR及浮力Fb的和大于移动体自身重力FG，此时，移动体依靠自上而下的机械推力FM平衡浮力与水力推力，保持静止；在移动体下落阶段中，随着流量Q的持续下降，在t=8.082 s时，流量低于开始落棒的临界流量Qc=1.99 kg/s，从而使 FG>FDR+Fb，且移动体所受合力向下，开始落棒运动。该过程中，浮力Fb及重力FG保持不变，落棒运动曲线主要取决于水力推力FDR的变化趋势。

图7 标准结构下落棒曲线

以低于1.99 kg/s的3组恒定定流量1.5、1.25、1.0 kg/s作为输入流量得到的PSS移动体下落特性为例，计算得到的位移与水力推力关系如图8所示。从中可以看到，在3组恒定流量下，移动体所受水力推力随着其位移x以近似的趋势发生变化。在移动体位移x=0~0.62 m区域内，移动体所受水力推力是逐渐减小的；当移动体落至位移x=0.62 m处时，此后区域移动体与外套管之间的流道截面有所缩小，水力推力自此处又略有提升。这样，在水力推力总体趋势随位移增加而降低，从而使移动体下落。在有液力自紧效果的前提下，又在流道截面缩小区域具有一定程度限制水力推力过快降低的缓冲趋势，且流量越小，缓冲效果越显著。而小的流量下，移动体有更大的速度，正需要更大的缓冲。

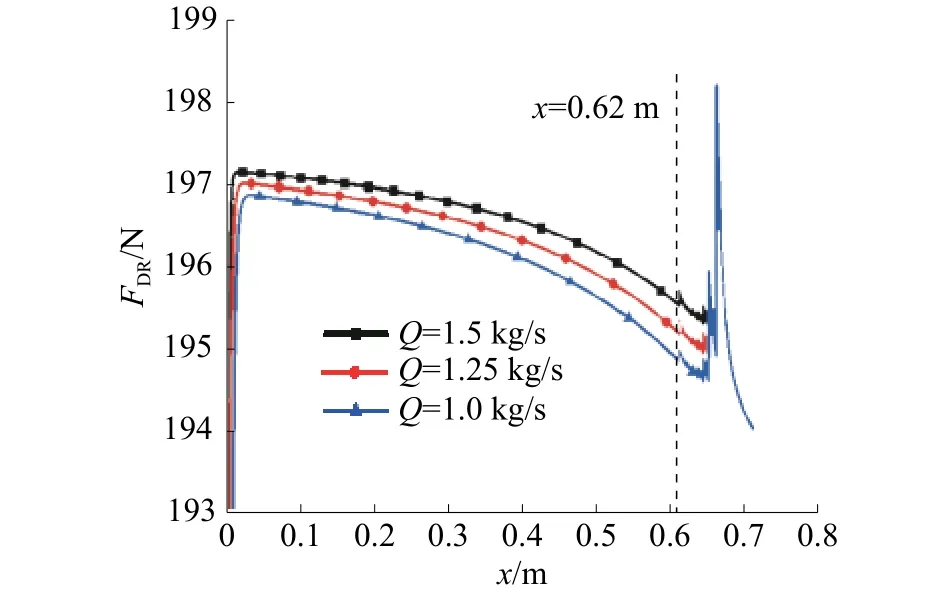
图8 定流量下移动体受力随位置变化关系

由于液力自紧效应与缓冲效果存在不相容的特性(液力自紧效应强时，缓冲效果弱；缓冲效果强时，液力自紧效应弱)，在设计缓冲区时，应考虑不同流量下移动体的落棒需求，对于液力自紧效应及缓冲效应做出取舍。流量较小导致移动体高速下落时应优先考虑缓冲效应；在流量较大使得移动体低速下落时，应优先考虑液力自紧效应。

5 PSS 结构敏感性分析

为了使设计的PSS在落棒时间、落棒临界流量等方面更好地满足停堆落棒要求，有必要针对不同的移动体结构流道以及外套管结构尺寸等，进行落棒敏感性计算分析，从而为优化PSS水力结构设计提供依据。对图9中所示的PSS几个关键结构，在各自设计可调范围内，选取不同结构尺寸，分别在与前述基准结构PSS落棒一致的惰转流量条件下，进行落棒计算。

图9 PSS 结构

选取进行敏感性计算的几个结构包括：1)移动体下节流孔(图2中流道3→9)；2)上节流孔(图2中流道15→16)；3)移动体上出口 (图 2中流道20→10)；4)移动体与外套管之间环缝[12]流道(图2中流道4→5)。针对这4个关键流道结构进行的落棒敏感性计算结果如下：

1)移动体下节流孔的尺寸敏感性计算结果

分别选取 2.5、5.0、7.5、10、12.5 mm 这 5 种下节流孔径进行落棒敏感性计算。落棒的位移−时间曲线如图10所示。可以看到：随着下节流孔径增大，移动体的落棒起始时间依次提前，但最大提前时间不超过0.3 s；开始落棒的临界流量也略有增大，但增大亦不超过0.022 kg/s；下节流孔各孔径下的落棒时间分别是7.491、7.461、7.441、7.432、7.429 s。总之，下节流孔孔径对移动体落棒性能影响不大。

图10 不同尺寸下位移随时间变化曲线

2)移动体上节流孔的尺寸敏感性计算结果

分别选取 2.5、5.0、7.5、10、12.5 mm 这 5 种上节流孔径进行落棒敏感性计算，得到的落棒位移−时间曲线如图11所示。可以看到：随着移动体上节流孔孔径的增加，移动体的落棒起始时间明显提前，最多提前4.362 s；相应开始落棒的临界流量亦随上节流孔径增加而增大，增加量最多达0.585 37 kg/s；而且落棒时间随着上节流孔孔径的增加而减小，移动体的落棒时间最大相差约1.54 s。可见该结构尺寸的选取对落棒性能影响较显著，设计时需结合落棒要求详细考虑优化选取。

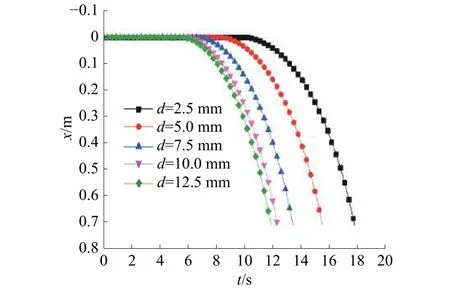
图11 不同尺寸下位移随时间变化曲线

3)移动体上出口腰型孔尺寸的敏感性计算结果

移动体上出口腰型孔直径分别选取1.0、3.0、5.0、7.0、9.0 mm这5种不同尺寸进行落棒敏感性计算，得到的落棒位移−时间曲线如图12所示。可以看到：在 3.0、5.0、7.0、9.0 mm 这 4 种尺寸下，移动体落棒的位移−时间曲线基本重合，尺寸影响不敏感；而上出口腰型孔直径降至1.0 mm时，落棒位移−曲线稍微显著一些，起始落棒时间略有延迟(延迟约0.5 s)，开始落棒的临界流量稍有降低(约降低 0.06 kg/s)，而落棒时间稍增加 (落棒时间约 7.612 s)。

图12 不同尺寸下位移随时间变化曲线

4)移动体−外套管间环缝宽度敏感性计算结果移动体与外套管间环缝宽度分别选用12、16、19、21、25 mm 这 5种不同的尺寸，进行落棒敏感性计算，得到的落棒位移−时间曲线如图13所示。由图13可知，移动体与外套管之间环缝宽度的变化对落棒特性影响甚微，不同尺寸下落棒起始时间、开始落棒临界流量以及落棒时间均差别不大。

图13 不同尺寸下位移随时间变化曲线

6 结论

本文针对快堆悬浮式非能动停堆组件移动体进行了落棒水动力及运动分析，开发了落棒运动分析程序PSSD。结合PSS基本结构，计算分析了移动体落棒性能，通过PSS移动体结构尺寸参数对落棒性能的敏感性计算分析，发现结构尺寸对于PSS性能的影响存在显著的差异，根据不同结构对于PSS性能影响的剧烈程度，得出以下3点PSS设计指导方案：1)上节流孔结构尺寸对移动体落棒性能影响较显著，在PSS设计中可作为调节PSS落棒性能的主要结构；2)移动体上出口孔尺寸对移动体落棒性能影响较小，可在确定上节流孔结构尺寸后，调节该组件尺寸，对PSS落棒性能进行精细调节；3)其他结构尺寸，如移动体下节流孔孔径、移动体−外套管间环缝宽度等则对落棒性能影响极小，可用于调节PSS其他性能(稳定性、耐腐蚀性等)。上述结论可支持非能动停堆机构PSS的结构设计与优化。