鄂尔多斯盆地低渗透致密砂岩气藏水平井分段多簇压裂布缝优化研究
杨兆中,陈 倩,李小刚,鲜 菊,冯 波,杜 冰
(1.西南石油大学油气藏地质及开发工程国家重点实验室,四川成都610500;2.中国石油新疆油田公司,新疆克拉玛依834000;3.中国石油西部钻探克拉玛依钻井公司,新疆克拉玛依834008;4.新疆克拉玛依红山油田有限责任公司研究所,新疆克拉玛依834000)
鄂尔多斯盆地蕴含丰富的油气资源,杭锦旗区块位于鄂尔多斯盆地北部,属于典型的低渗透致密砂岩气藏。目前,现场一般采用水平井分段压裂技术进行增产改造。水平井压裂后产能预测可有效评价压裂改造效果,以产能为目标函数可优化裂缝参数及布缝方案[1-6]。现在尚未有成熟的压裂水平井产能计算软件供现场使用。因此,有必要建立符合实际的水平井分段压裂产能预测模型,并编制简单高效的产能计算软件。GIGER等首次建立数学模型来研究压裂水平井产能,但是该模型不能很好地耦合流体的流动过程[7]。SOLIMAN等在此基础上,将裂缝中流体的流动考虑为径向流,得到单一裂缝下水平井产能,再通过产能叠加得到多条裂缝下水平井产能[8]。OZKAN等研究单裂缝的解析法,运用叠加原理得到压裂后水平井产能[9],但是,该方法对裂缝进行理想化简化,即水力裂缝垂直水平井筒及裂缝间距相等,并忽略裂缝间的相互干扰。中国学者开展了大量关于分段压裂水平井产能的研究[10-15],郎兆新等运用复位势理论推导水平井产能公式[16-18],该解析方法理论较为成熟。徐严波等通过离散裂缝,应用复位势理论和势叠加原理等,建立压裂水平井多条裂缝相互干扰的产能计算新模型[19]。曾凡辉等在此基础上,考虑压裂水平井裂缝段产量非均匀流入、裂缝内变质量以及多裂缝间的相互干扰,采用空间和时间离散技术,建立低渗透油藏压裂水平井储层渗流和裂缝流动相耦合的非稳态产量计算模型[20]。何军等在裂缝离散的基础上,应用无限大地层点汇位势理论、势叠加原理及矩阵变换方法,推导了单裂缝压裂水平井和多裂缝压裂水平井产能计算线性方程组[21]。前人均未考虑启动压力梯度,且对裂缝做了理想化假设,未讨论不同裂缝形态及布缝方案对水平井产能的影响。因此,笔者基于点汇法离散裂缝,运用位势理论和势叠加原理,考虑缝间干扰及启动压力梯度、耦合储层渗流与裂缝流动,推导低渗透致密砂岩气藏压裂水平井非稳态产能计算模型,并分析不同裂缝形态及布缝方案下的水平井产能。

1 分段压裂水平井产能模型建立
1.1 物理模型
低渗透致密砂岩气藏水平井分段压裂后,流体流动过程为:基质—裂缝—水平井井筒。物理模型假设条件如下:①无限大地层均质各向同性,且顶底封闭,水平井井筒位于气藏中部;②气体在低渗透致密砂岩气藏基质中流动存在启动压力梯度,裂缝内渗流符合达西定律;③裂缝垂直于水平井井筒,且完全穿透产层;④气体在基质和裂缝中等温渗流,且只通过裂缝流向水平井井筒。
前人研究结果[22-23]表明,水平井套管射孔完井段内多簇裂缝在竞争延伸过程中会产生明显的应力干扰作用,外侧裂缝在延伸过程中发生偏转,形成弯裂缝,模拟结果如图1所示。
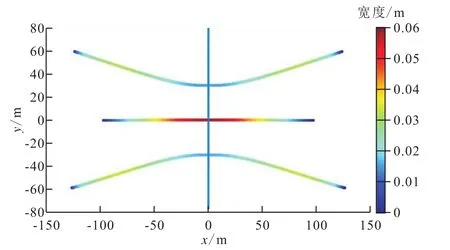
图1 弯裂缝示意Fig.1 Schematic of curved fracture
1.2 数学模型
以无限大地层中任一点的压降公式为基础,建立不稳定渗流偏微分方程为:
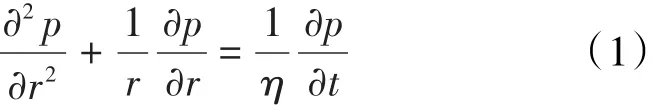
初始条件为:
边界条件为:
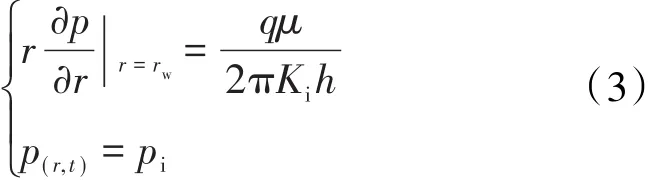
通过以上偏微分方程,结合气体拟压力函数及平面直角坐标转换,可得无限大地层定流量点汇的压降公式为:
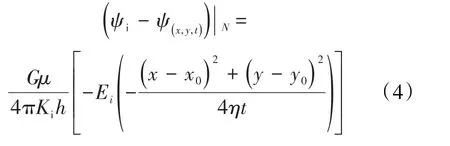
每一簇弯裂缝离散后均形成n个点汇(图2)。以水平井井筒和裂缝为基准建立坐标系(图3),无论裂缝形态如何,均可以根据每个点的坐标,得到第i簇裂缝第j个点汇对储层中某点产生的压降。由位势理论和势叠加原理,推导N簇裂缝存在时,t时刻无限大地层中某点(x,y)产生的压降表达式为:
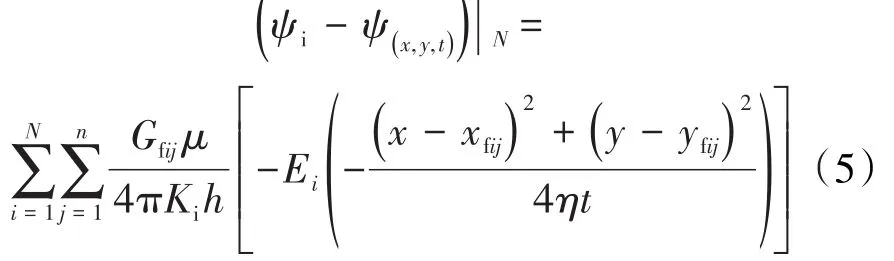
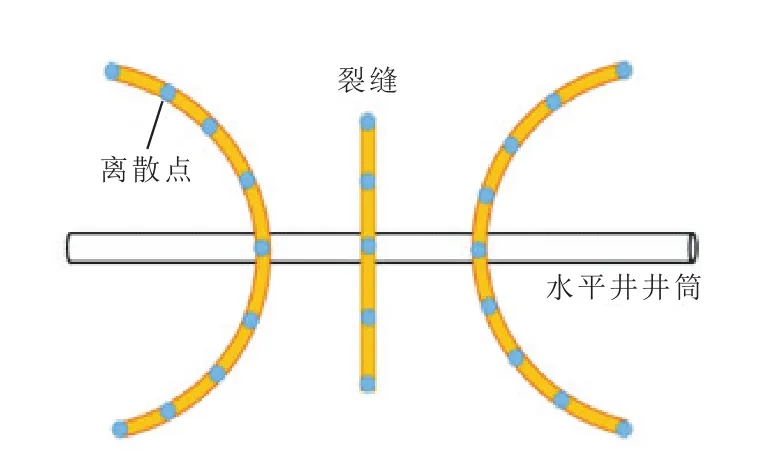
图2 离散裂缝示意Fig.2 Schematic of discrete fracture

图3 坐标系示意Fig.3 Fracture distribution and its coordinate
在低渗透致密砂岩气藏中,由于储层物性差,往往存在启动压力梯度。将启动压力梯度项引入(5)式,则第i簇裂缝左翼尖端压降公式为:
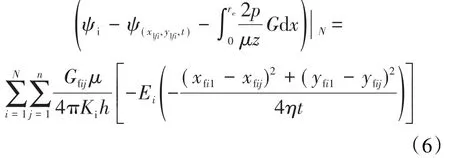
同理可得第i簇裂缝右翼尖端压降公式为:

由于裂缝左右翼存在差异,因此将端部2个压力的平均值作为第i簇裂缝的端部压力,即:
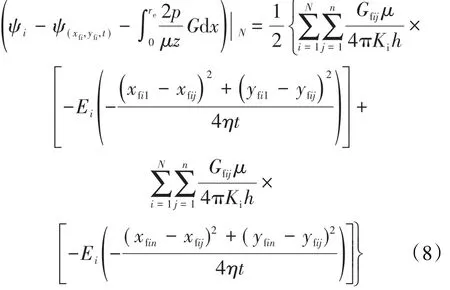
考虑真实气体,将拟压力函数转化为压力,则:
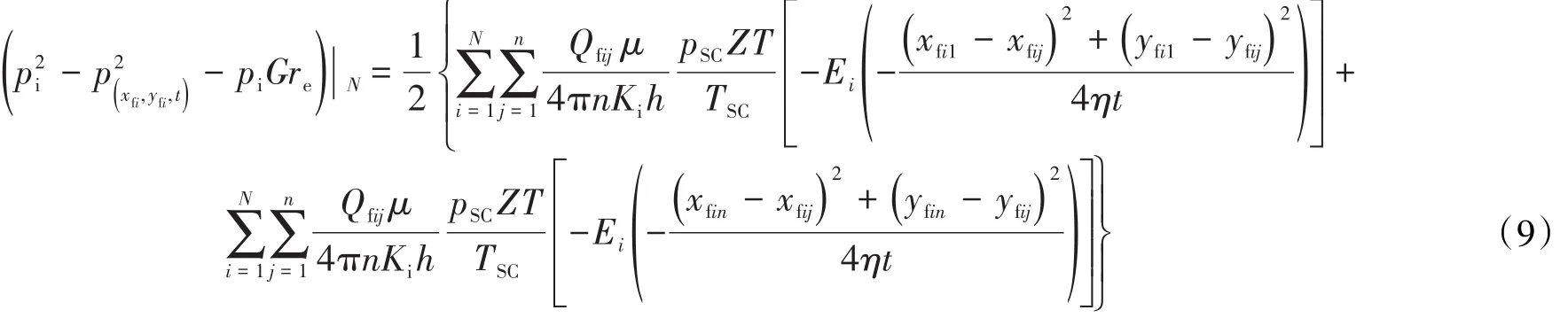
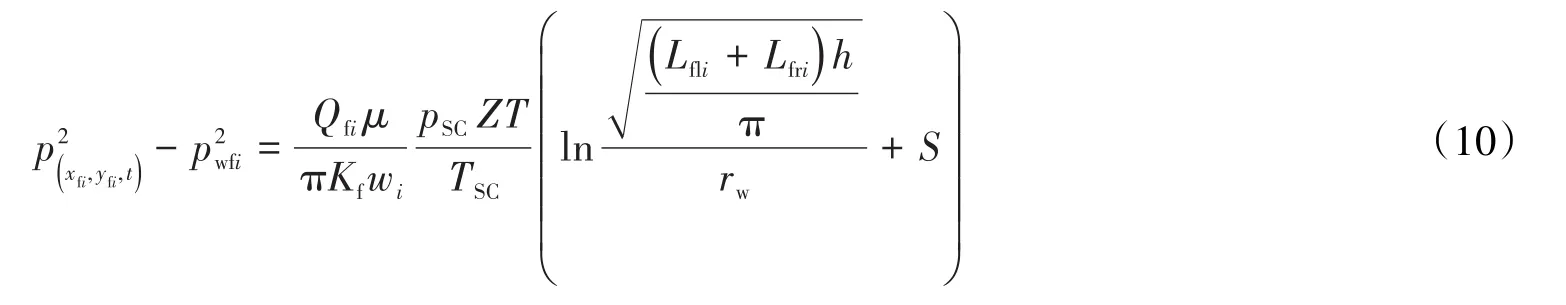
对流体从地层到裂缝、裂缝到井筒的压降公式 进行耦合,将(9)式代入(10)式得产能预测模型为:

考虑气体从裂缝尖端到井筒的流动为拟径向 流,井筒周围存在表皮伤害,引入表皮系数可得:
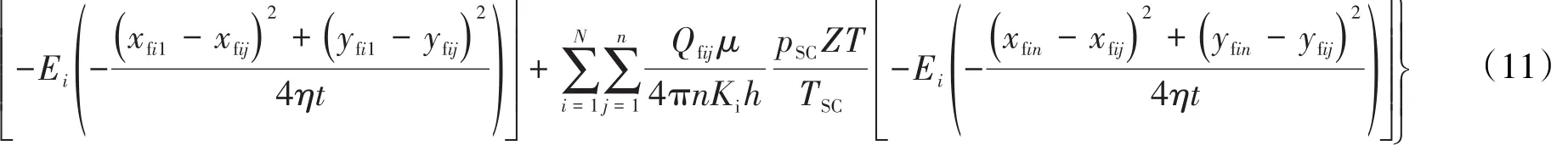
建立低渗透致密砂岩气藏考虑启动压力梯度及缝间干扰的压裂水平井产能预测模型,每簇裂缝可以得到1个方程,含有N个未知数的N个线性方程组构成该模型。求解该线性方程组可得每簇裂缝的产量,求和即可计算水平井的产量,即:
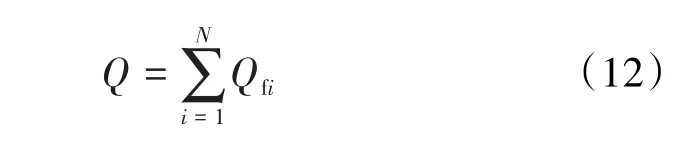
2 实例应用
鄂尔多斯盆地杭锦旗区块锦58井区盒3层基础数据包括:有效储层厚度为10 m,基质孔隙度为8.56%,基质渗透率为0.45 mD,地层温度为94℃,原始地层压力为26 MPa,地层压缩系数为3×10-4MPa-1,气体黏度为0.02 mPa·s,天然气偏差因子为0.957。水平井分段多簇压裂每一段形成3簇裂缝,若裂缝不转向则形成常规的直裂缝。2种形态裂缝的总裂缝半长在平面内相等,缝高与储层厚度一样。根据建立的产能预测模型((11)式),分别计算弯裂缝和直裂缝2种情况下的日产量和累积产量。
从模拟结果可以看出,弯裂缝与直裂缝日产量差值在2×104m3以内,弯裂缝的产量较高;随着生产的进行,弯裂缝与直裂缝日产量差值逐渐变小,且稳定在0.5×104m3左右(图4)。在生产初期,弯裂缝与直裂缝累积产量差值较小,随后逐渐变大(图5)。因此,水平井压裂形成的弯裂缝比传统直裂缝的增产效果好,前人对裂缝做出的理想化假设导致计算产量偏小。
当簇间距较小时,由于较强的缝间应力干扰作用,外侧裂缝将发生严重弯曲,同时抑制中间裂缝的延伸。当簇间距过大时,外侧裂缝由于受干扰较弱则不会发生弯曲。因此,建议采用偏小的簇间距,但可以通过调整射孔完井参数(如射孔数、孔眼直径)使中间裂缝变长,同时获得弯曲的外侧裂缝[18]。
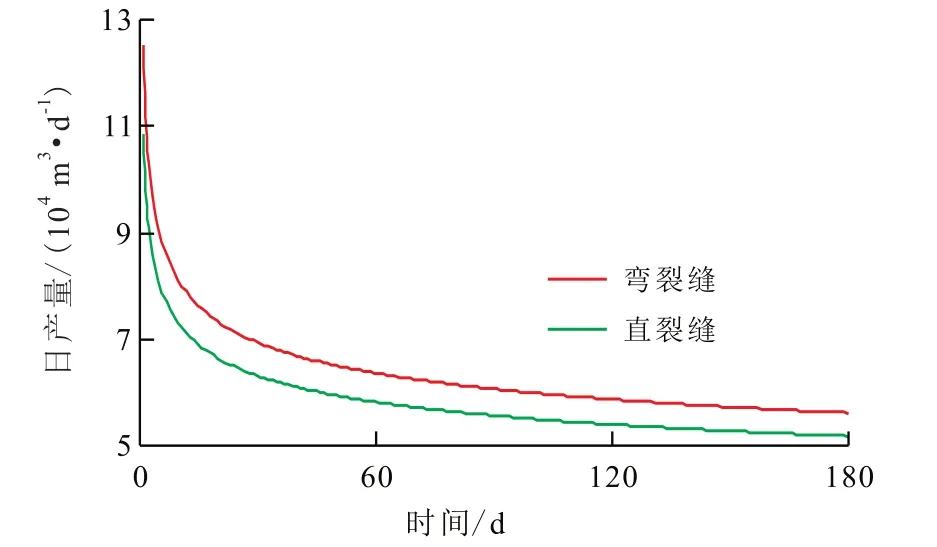
图4 3簇裂缝日产量Fig.4 Daily production rate for three cluster fractures
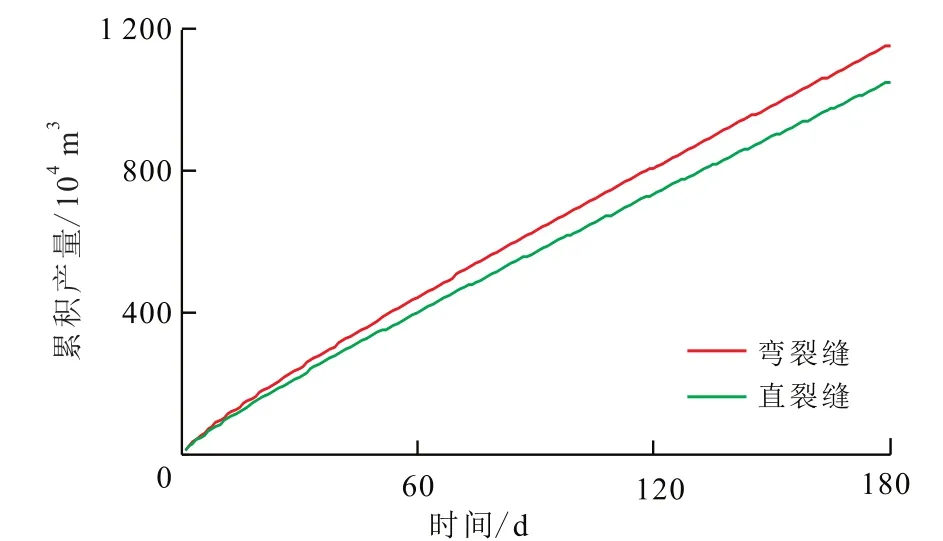
图5 3簇裂缝半年累积产量Fig.5 Cumulative production of three cluster fractures in half a year
3 布缝方案优化
不同的裂缝形态及布缝方案对水平井产能影响较大,因此,基于现场情况及理论研究,在每段3簇和4簇裂缝下,选取裂缝导流能力、总裂缝半长、缝长比、间距比这4个裂缝参数,得到最优的布缝方案。正交试验设计是研究多因素多水平的一种设计方法,通过对正交设计试验计算结果进行分析,可以得出压裂水平井的主要裂缝参数对产能的影响程度。裂缝参数包括:裂缝导流能力分别为30,40和50 D·cm,总裂缝半长分别为300,400和500 m,缝长比(Lf1/Lf2)分别为0.5,1和2,间距比(d1/d2)分别为1和2。根据4个裂缝参数作出4因素3水平正交试验方案(表1,表2)。
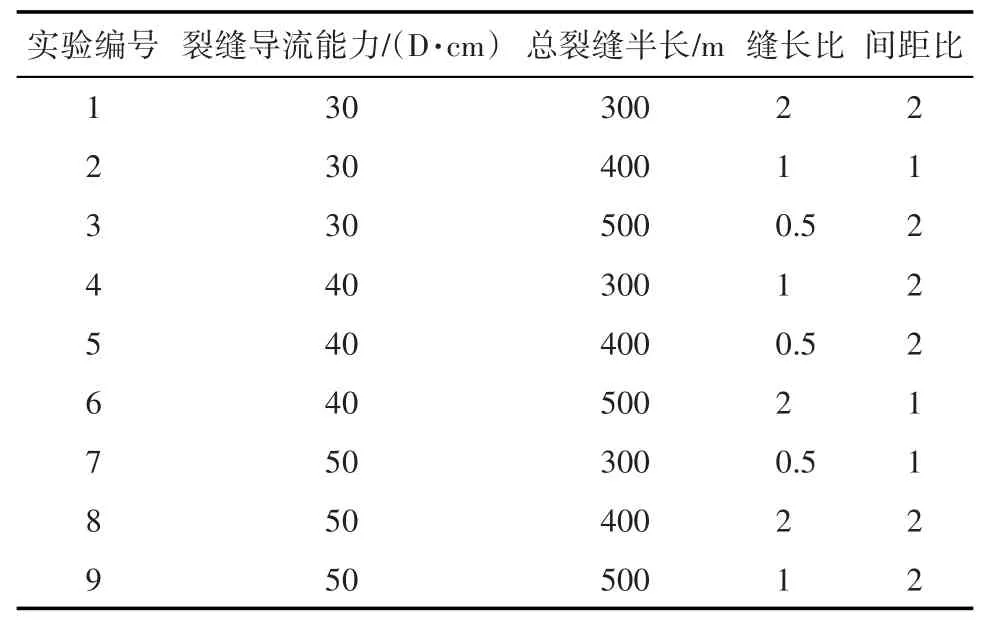
表1 3簇裂缝正交试验Table1 Orthogonal test of three cluster fractures
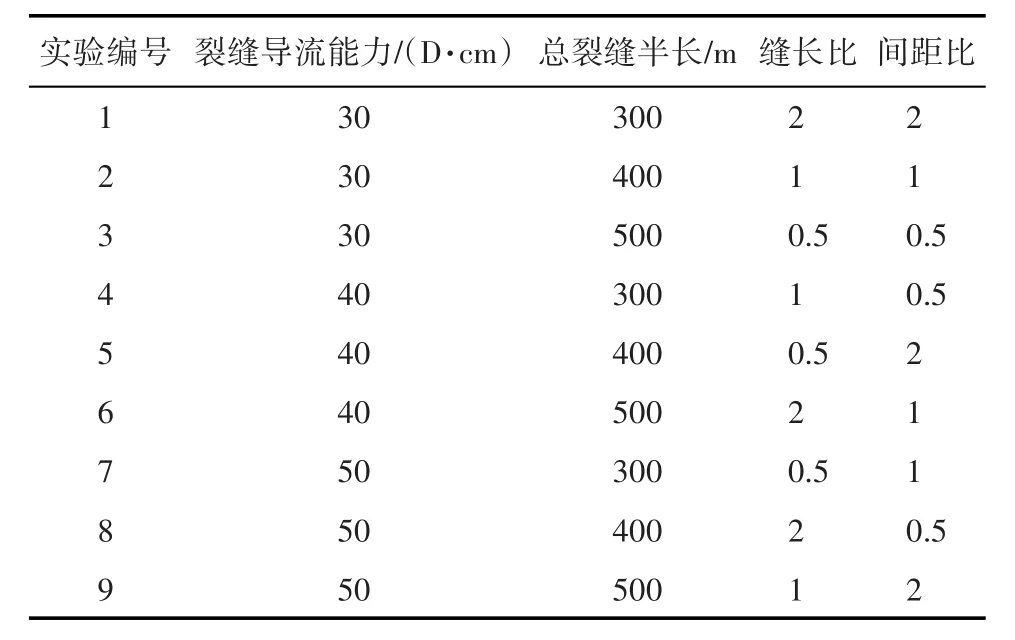
表2 4簇裂缝正交试验Table2 Orthogonal test of four cluster fractures
由每段3簇裂缝的9组正交试验结果(图6)分析得出每个裂缝参数的最优值,即裂缝导流能力为50 D·cm,总缝长为500 m,缝长比为2,间距比为2。该最优组合下的布缝方案,增产效果最好。在每段4簇裂缝的9组正交试验结果(图7)中,180 d累积产量最高的布缝组合与每段3簇裂缝的相同,因此推荐杭锦旗区块水平井分段多簇压裂段内布缝方式为“U”型,即两边长、中间短,且采用非均匀布缝模式,对每段4簇裂缝采用“两边疏,中间密”。

图6 3簇裂缝不同方案下的累积产量Fig.6 Cumulative production of three cluster fractures under different schemes
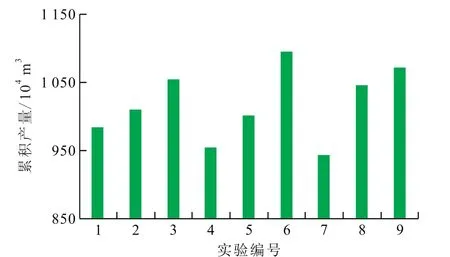
图7 4簇裂缝不同方案下的累积产量Fig.7 Cumulative production of four cluster fractures under different schemes
正交试验各影响因素水平对目标的效应极差可以反映主次因素的顺序。分析每段3簇裂缝和4簇裂缝的效应曲线(图8,图9),得到不同裂缝因素对低渗透致密砂岩气藏水平井分段多簇压裂产能的影响由强到弱依次为总裂缝半长、缝长比、裂缝导流能力、间距比。总裂缝半长越长,水平井产量越高。但总裂缝半长与经济成本相关,不能一味追求长缝增产,因此在一定经济条件下,应该适当增加裂缝总长以提高天然气产量。
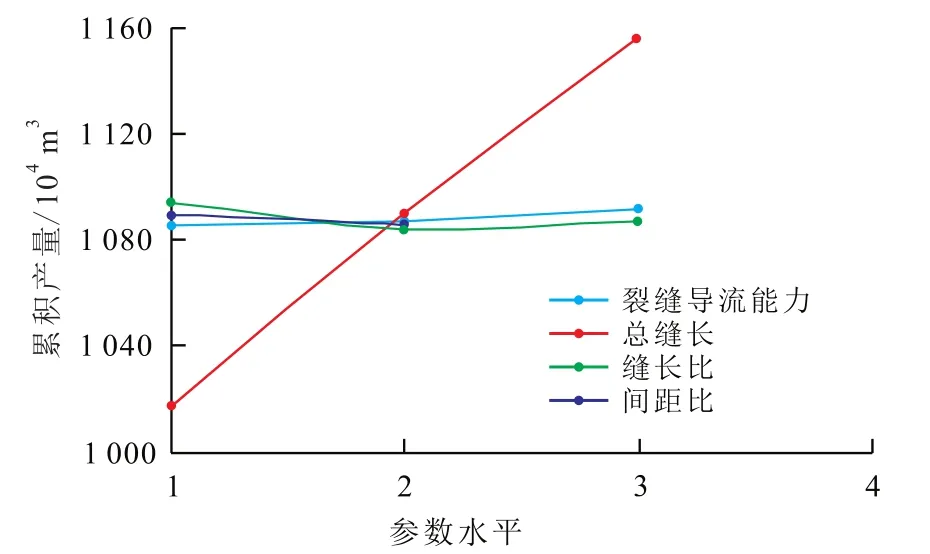
图8 3簇裂缝的效应曲线Fig.8 Effect curve of three cluster fractures
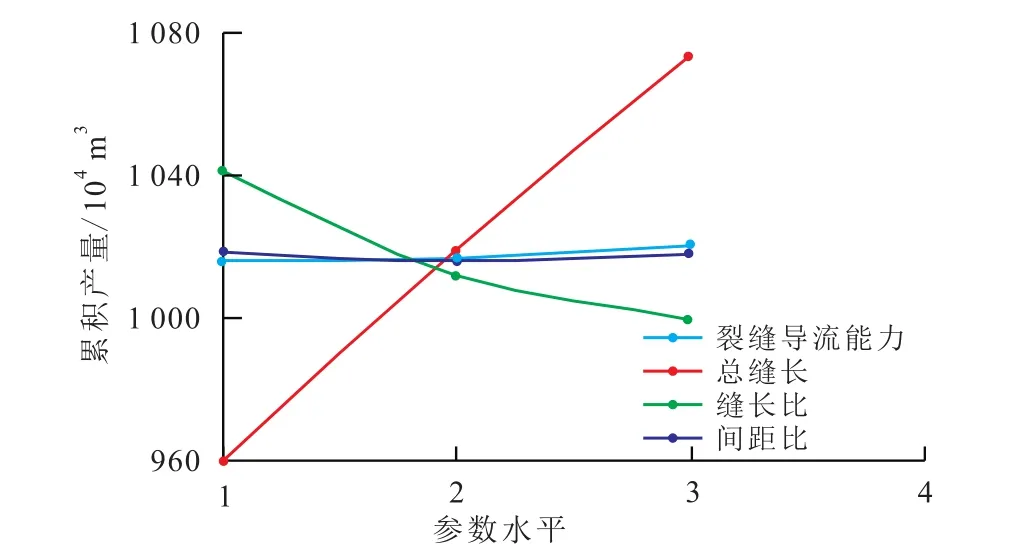
图9 4簇裂缝的效应曲线Fig.9 Effect curve of four cluster fractures
4 结论
在低渗透致密砂岩气藏中,考虑启动压力梯度的影响,通过点汇法离散裂缝,再根据位势理论和势叠加原理,建立考虑裂缝间相互干扰的低渗透致密砂岩气藏压裂水平井非稳态产能计算模型。将裂缝离散成n个点汇,不仅可以计算直裂缝的产量,还可以计算因应力干扰而转向的弯裂缝的产量。
以鄂尔多斯盆地杭锦旗区块锦58井区盒3储层为靶区,将水平井压裂形成的弯裂缝与常规直裂缝的日产量与累积产量进行对比,结果表明弯裂缝的产量更高,增产效果更好,前人对裂缝作出的理想化假设导致计算产量偏小。
针对不同裂缝参数分别建立了每段3簇和每段4簇裂缝的9组正交试验,研究了每段不同裂缝簇数条件下裂缝参数对于水平井压裂产能的影响规律。结果显示,每段3簇裂缝以及每段4簇裂缝所得计算结果一致,即裂缝参数对压裂产能的影响由强到弱依次为总裂缝半长、缝长比、裂缝导流能力、间距比,优选出的最佳每段多簇压裂布缝方案为“U”型布缝以及非均匀布缝模式,其中,每段4簇裂缝条件下建议“两边疏、中间密”进行布缝。
符号解释:
p——压力,MPa;r——径向距离,m;η——导压系数,µm2·MPa(/mPa·s);t——时间,s;p(r,0)——0时刻的地层压力,MPa;pi——原始地层压力,MPa;rw——井半径,m;q ——产量,m3/s;µ ——气体黏度,mPa·s;Ki——储层渗透率,D;h ——储层厚度,m;p(r,t)——t时刻的地层压力,MPa;ψi——原始地层拟压力,MPa2(/mPa·s);ψ(x,y,t)——t时刻地层任一点处的拟压力,MPa2(/mPa·s);x——横坐标变量,m;y——纵坐标变量,m;N——裂缝数,簇;G——启动压力梯度,MPa/m;Ei——幂积分函数;x0——气藏中任一点的横坐标,m;y0——气藏中任一点的纵坐标,m;Gfij——第i簇裂缝j点质量流量,kg/s;i——裂缝数,簇,其值为1,2,…,N;j——每簇裂缝离散点个数,个;xfij——第i簇裂缝j点的横坐标,m;yfij——第i簇裂缝j点的横坐标,m;ψ(x ,y,t)——第i簇裂缝左lfilfi翼尖端平均拟压力,MPa2(/mPa·s);xlfi——第i簇裂缝左翼尖端横坐标,m;ylfi——第i簇裂缝左翼尖端纵坐标,m;xfi1——第i簇裂缝第1个点的横坐标,m;yfi1——第i簇裂缝第1个点的纵坐标,m;ψ(x,y,t)——第i簇裂缝右翼尖端平均拟压rfirfi力,MPa2(/mPa·s);xrfi——第i簇裂缝右翼尖端横坐标,m;yrfi——第i簇裂缝右翼尖端纵坐标,m;xfin——第i簇裂缝第n个点的横坐标,m;yfin——第i簇裂缝第n个点的纵坐标,m;re——供给半径,m;z——气体压缩因子;ψ(x ,y,t)——第 i簇裂fifi缝尖端平均拟压力,MPa2(/mPa·s);p(x,y,t)——裂缝尖端平均fifi压力,MPa;pSC——标准状态压力,MPa;Z——气体偏差因子;T——储层温度,K;TSC——标准状态温度,K;Qfij——第i簇裂缝第j点的气体流量,m3/s;n——离散点汇数,个;pwfi——井底流压,MPa;Qfi——第i簇裂缝的产量,m3/s;Kf——裂缝渗透率,µm2;wi——裂缝宽度,m;Lfli——第i簇裂缝左翼长度,m;Lfri——第i簇裂缝右翼长度,m;S——表皮系数;Q——水平井产量,m3/s。

