基于k领域快速搜索的改进ICP算法在管道检测中的应用
孙 翌,包建东
(南京理工大学 机械工程学院,江苏 南京 210094)
0 引 言
近年来,随着我国工业管道施工技术的发展,对金属管道内凹槽磨损等疵病的检测提出了越来越高的要求,其严重者会直接影响到管道泄漏问题,因此对管道内壁的检测十分重要.传统的方法是采用激光位移传感器扫描管道内壁,将采集的多段数据进行拼接处理呈现完整的三维立体轮廓图,但在面对大量点云数据时,拼接过程耗时巨大,效率低下,无法满足日益增长的检测需求,为解决这一问题,本文对传统的算法做了研究,并在此基础上进行了改进,通过仿真和现场试验,证明其可行性.
1 传统ICP算法
对点云数据进行拼接常用的方法是Besl提出的最近点迭代算法[1](Iterative Closest Point,ICP),其核心是通过求得旋转矩阵R和平移向量T,把不同坐标系下测得的数据点云进行坐标变换,主要分为4个阶段[2]:
1) 对原始点云数据进行采样.
面对大量的点云数据,可先对其进行采样,以提高拼接速度,减少噪音点.
2) 确定初始对应点集.
根据确立对应点集的方法,大致分为3类: 点到点,点到投影,点到面.
3) 去除错误对应点对.
一般情况下,在确立初始对应点集中会存在大量的错误对应点对,因此需要一种约束方法去除错误对应点对,常用的有基于曲线几何特征的约束方法和基于刚性运动一致性的约束方法.
4) 坐标变换的求解.
该阶段为本算法的核心,对于旋转矩阵R和平移矢量T的求值,通常可采用以下4种方法: 单位四元数法、 奇异值分解法、 正交矩阵法和对偶四元数法.
2 基于k领域搜索的改进ICP算法
在确认初始点集与去除错误对应点对时,面对大量的点云数据,常用的方法在精度以及计算时间上都有一定的局限性,因此本文将采用一种基于自适应空间球的k最近领域快速搜索算法,来提高点云拼接ICP算法的迭代精度和速度.
2.1 基于自适应空间球的k最近领域快速搜索算法
传统的ICP算法搜索是计算任一点到其余各点的欧氏距离,然后升序排序,前面的k个点即为此点的k领域点,但随着点云数据规模的不断增大,这种方法耗时巨大,故本文将采用与k无关的分块策略对整个点云空间分块,以候选点所在子块的采样点近似密度确定初始动态球半径,以球的外切立方体搜索k领域候选点,当k领域候选点数目不满足要求或搜索不成功时,以外切立方体的外接球扩大搜索范围,直至满足要求或邻域搜索成功[3].
1) 点云空间分块
在一组点云数据中,共有N个采样点,设一立方体恰好将所有采样点全部围住,其体积为V; 将立方体分为若干个子空间,每个子空间内点云数目为num,则子空间边长L为[4]
(1)
式中:xmax,xmin分别为点云空间中在x方向的最大值和最小值;ymax,ymin分别为点云空间中在y方向的最大值和最小值;zmax,zmin分别为点云空间中在z方向的最大值和最小值.
2) 计算子空间中任意一点p的初始动态球半径,公式如下
(2)
3) 以p为圆心,r为半径确定p的动态球O0,计算O0的外切立方体A0, 位于外切立方体内的点则成为k邻近候选点,其数目为K.
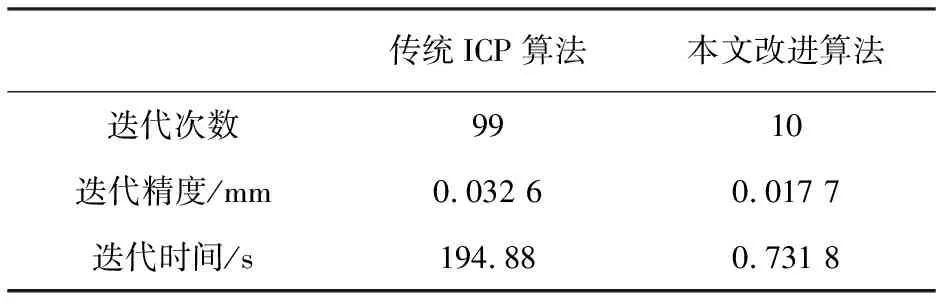
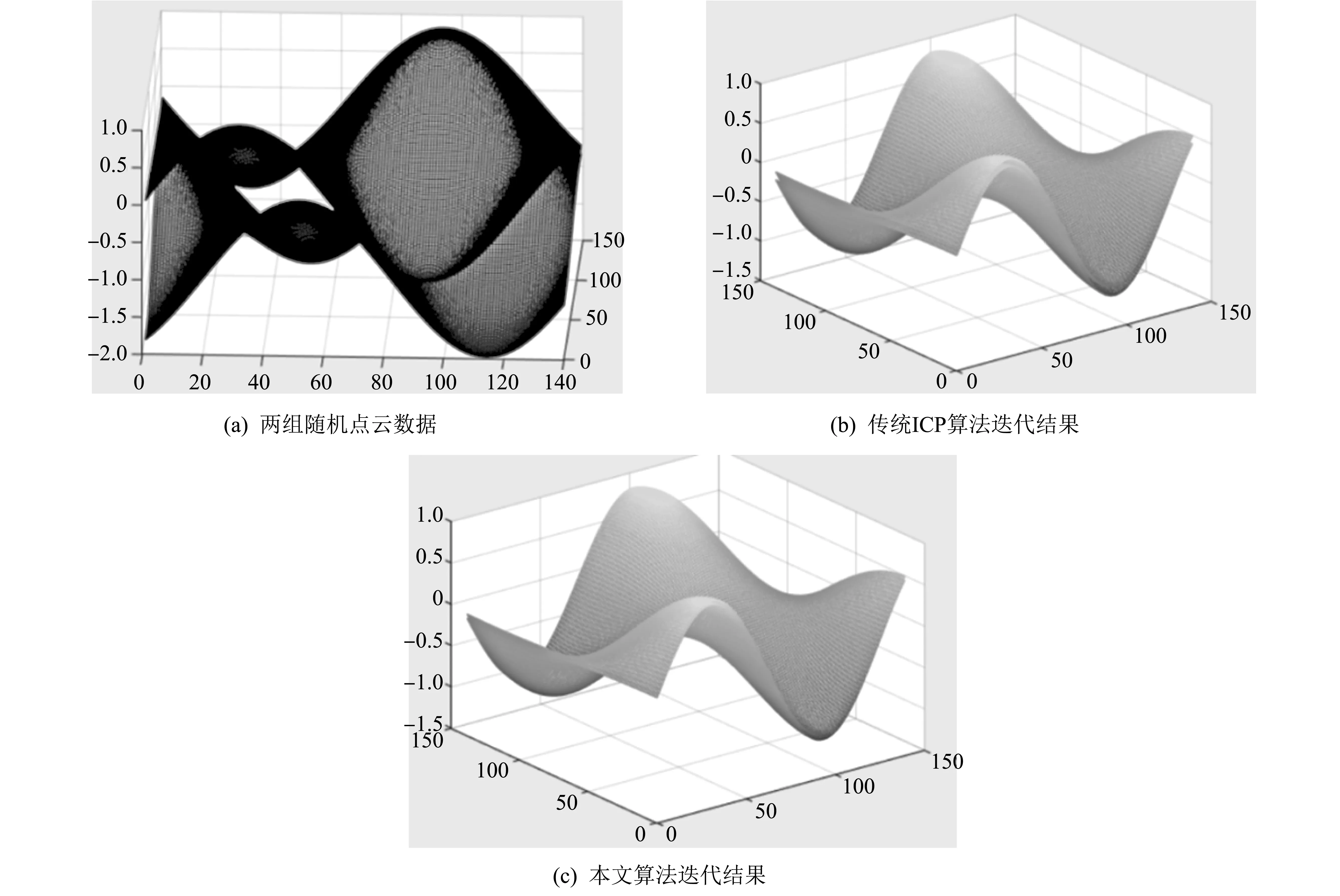
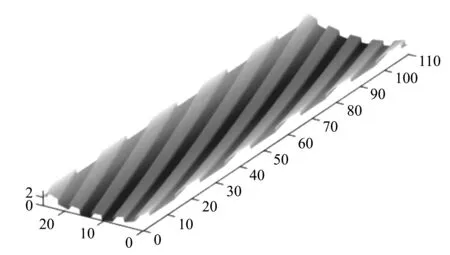
4) 若K 本文采用基于刚性运动一致性的约束方法去除错误对应点对,此类方法直接利用了刚性运动应保持被测物体重叠区域对应点不变的原理,利用候选对应点对间的距离约束排除错误对应点对[5]: 若(p1,q1)与(p2,q2)为正确对应点对,则由刚性运动一致性约束应有‖p1-q2‖=‖(q1-p2)‖,考虑到实际点云数据不可能完全满足上式,故本文采用如下标准 (3) 式中:δ为事先给定的阈值(文中取10%). 本文采用奇异值分解算法[6](Singular Value Decomposition,SVD)来进行坐标变换的求解. 对于A∈Rm×n,则必然存在U=[μ1,…,μm]∈Rm×n与V=[v1,…,vn]∈Rm×n使下式成立 (4) 式中: ∑r=diag(σ1,σ2,…,σr),σ1≥σ2≥…≥σr>0,μi为第i个左奇异向量,vi为第i个右奇异向量. 为求得旋转矩阵R与平移向量T,对最终确立的对应点点集P与Q进行如下操作: 1) 分别计算点集P与点集Q的重心 (5) 2) 构造一个3×3矩阵H (6) 3) 利用奇异值分解法对矩阵H进行分解得到矩阵U和V,分解结果如下 H=UΛVT, (7) 式中:Λ为对角矩阵,Λ=diag(d1,d2,d3),d1≥d2≥d3≥0. 4) 如矩阵U与V满足以下条件,则矩阵A (8) 5) 可得到旋转矩阵R与平移向量T分别为 (9) 该算法在一次迭代后如无法满足需求,需在此基础上重新匹配对应点集后进行迭代求解. 本文利用MATLAB随机生成两组点云数据,使用传统ICP算法与本文改进ICP算法拼接进行比较,其结果如图 1 及表 1 所示. 表 1 仿真数据拼接结果 图 1 迭代结果Fig.1 The iteration results 传统ICP算法达到收敛条件时其迭代次数达到了99次,精度为0.032 6 mm,耗时194.88 s.本文的改进算法仅迭代10次,耗时0.731 8 s,且精度达到了0.017 7 mm. 由表 1 所知,本文改进的ICP算法在算法迭代次数、 精度与速度上都有了极大的改进,能够确实有效地提高实际检测效率. 图 2 为本文设计的管道内壁激光检测装置,现场实验图如图 3 所示,步骤如下: 1) 直行电机以4.4 mm/s的速度带动装置匀速前行,激光位移传感器的采样频率为3 000 Hz,y方向轮廓间距约为0.001 5 mm. 2) 起始位置位于炮口有膛线处,每次爬行到管道尾端结束此次测量. 3) 旋转电机以20 °/s的速度旋转,每次测量60°范围内的管道,以152口径为例,可测得25.3 mm 宽的数据,每个数据点之间的间隔(即x方向)约为0.002 8 mm,共分6次测量完整管道. 4) 对采集到的数据进行处理、 拼接等后续工作,可得到内膛表面完整的三维轮廓图. 图 2 管道内壁激光检测装置Fig.2 A laser detection device for the inner wall of the pipe 图 3 现场实验图Fig.3 Field experiment 图 4 为管道内壁激光检测设备工作25 s后根据数据形成的图像,原数据共有75 000个点,经过数据处理后,形成了宽25.3 mm,长约110 mm的三维轮廓图; 图 5 为两个点云数据拼接后的宽50.6 mm,长110 mm的图像. 由实验结果可知,通过该设备采集的数据进行处理得到的三维轮廓图像,较好地描述了管道内壁的实际情况,可直观清楚地了解到管道内壁的各种信息,对判断疵病损伤有极大的帮助. 图 4 初始轮廓图Fig.4 Initial contour 图 5 轮廓拼接图Fig.5 Contour splicing 本文以一种管道内壁激光检测装置为例,简要介绍了它的工作原理,重点介绍了采集的点云数据的一些处理算法,包括传统ICP算法和基于k领域快速搜索的改进ICP算法,特别是改进后的ICP算法较原ICP算法迭代次数减少了十倍,迭代精度也有较高的提升,更是极大地缩短了迭代时间,这对提高点云数据的拼接效率有极大的帮助,证明改进后的ICP算法可有效应用于管道内壁检测领域中.2.2 去除错误对应点对
2.3 奇异值分解法
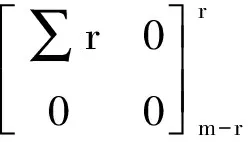

3 仿真分析
4 现场试验



5 结 论

