基于MOABCO的多目标测试用例优先级排序
张 娜,张 唯,吴 彪,包晓安
(1.浙江理工大学 信息学院,浙江 杭州 310018; 2.山口大学 东亚研究科,山口 753-8514)
0 引 言
随着工业程序的日益复杂,将代码覆盖率、 测试需求覆盖、 平均错误检测率等因素之一作为测试用例排序准则的单目标测试用例优先级技术(Test Case Prioritization,TCP),已经难以满足回归测试的测试需求,研究者们亟需将研究重心转移至多目标测试用例优先级排序(Multi-Objective Test Case Prioritization,MOTCP)问题上[1].根据排序方法的不同,已有的关于MOTCP问题的研究可以分为加权法[2-6]和Pareto最优法两类[7-10],其中加权法占大多数,Pareto最优法的相对较少.同时,Pareto最优法的研究算法主要集中在以NSGA-II算法为代表的进化算法,关于其他智能搜索算法的研究还相对较少.
MOTCP问题从本质上来说是求解最优测试用例执行次序的组合优化问题[11],可以描述为: 对于给定的测试用例集T,PT为T的全排列集合,目标函数向量F=[f1(p),f2(p),…,fi(p),…,fM(p)],fi表示第i个优化目标的目标函数,fi∶PT→R,p∈PT,1≤i≤M.要求找到一个PT′属于PT,使∀p′∈PT′∩F达到Pareto最优.人工蜂群算法(Artificial Bee Colony Algorithm, ABC)相对于其他智能搜索算法具有结构简单、 控制参数少、 易于实现等特点[12].基于ABC算法的多目标人工蜂群优化(Multi-Objective Artificial Bee Colony,MOABC)算法,在解决多目标组合优化问题上表现出良好的特性[13,14].因此,可将MOABC算法引入到解决MOTCP问题中.
本文针对已有MOABC算法存在易陷入局部最优等问题,对外部精英解集及全局最优解的更新、 局部搜索和蜜源选择方式上做出了改进,提出了一种MOABCO算法.将测试用例的平均语句覆盖率和有效执行时间作为优化目标,并用MOABCO算法求Pareto最优解,以解决MOTCP问题.
1 多目标人工蜂群优化算法
基本的MOABC算法除了增加外部候选解集,在雇佣蜂、 观察蜂和侦查蜂三个阶段的操作均与标准ABC算法相同,本文在基本MOABC的基础上进行改进.
1.1 精英解集及全局最优解更新策略
在基本的MOABC算法中,当某个蜜源经过limit次的开采后没有开采价值时与之对应的雇佣蜂转化为侦查蜂,并按照式(1)随机产生一个新蜜源代替.
xij=xmin,j+rand(0,1)×(xmax,j-xmin,j),
(1)
式中:xij为新蜜源的第j维分量,j∈{1,2,…,D},rand(0,1)为范围在(0,1)内的一个随机数,xmax,j和xmin,j分别为蜜源第j维分量的上下界.
为了充分利用所搜过程中所产生的非劣解(蜜源),提高算法的收敛性和多样新,本文在外部建立精英解集,精英解集的更新策略,如下算法1所示.
算法1:
输入: 外部精英集M,精英集的最大容量m,新蜜源个体S
输出: 外部精英集M
If (个体S至少被M中的一个个体支配)
外部精英集M不更新;
Else if (个体S支配M中的某些个体)
将外部精英集M中被S支配的个体删除,并将S加入到M中;
Else
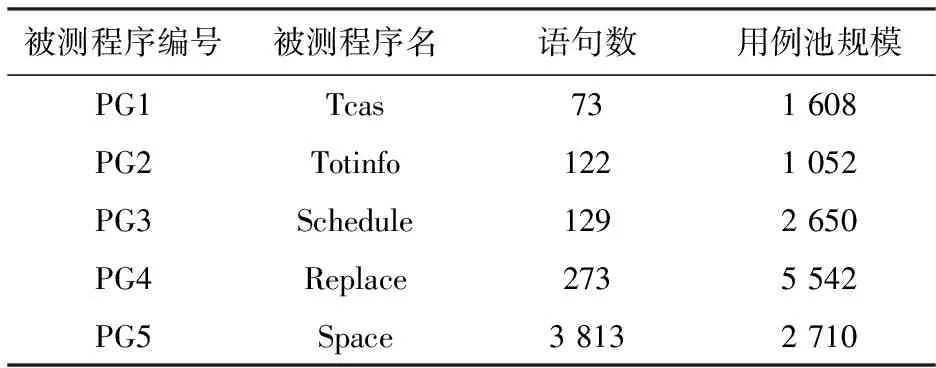
if (外部精英集M中个体的个数 将S加入到外部精英集M中; Else If (个体S在外部精英解集的最拥挤区域) 不更新外部精英集M; Else 用个体S替换外部精英解集中最拥挤区域的个体,更新外部精英集M; End if 在外部精英解集中,每一个非支配解相对其他的解而言都是最优的,而在算法运行过程中,只需要选取一个作为全局最优解.拥挤距离d(i)用于描述精英解集中某个解的密度值,本文首先计算精英解集中每个解的d(i)值并降序排列,取d(i)值大的前50%的精英解(即,处于Pareto前端的分散个体)作为全局最优解的候选者.拥挤距离的计算公式如式(2)所示, (2) 为了提高精英解集中个体的多样性,同时使其均匀分布在目标空间上,本文采用如式(3)的随机选法. (3) 式中:Num为非劣解的个数,xbest为全局最优解,A为精英解集中拥挤距离值较大的前50%的个体的集合,rand_int(0,i)为产生(0,i)内随机正整数的函数. 已有的研究表明,充分利用精英解的特征信息能够有效地促进种群进化[15].而基本的MOABC算法在局部搜索过程中采用随机选择的方式挑选一个可行解作为局部搜索的引导信息,按照式(4)进行搜索并根据贪婪选择机制对蜜源进行更新,忽略了精英个体的引导作用. (4) 式中:i,k∈{i=1,2,…,N}且i≠k,j∈{i=1,2,…,D},R为[-1,1]中的随机数. 同时,差分变异策略是差分进化算法中的变异方法,通过种群个体间的差分向量对个体进行扰动,实现个体的变异,能够有效利用群体分布特性,提高算法的搜索能力.本文将差分进化算法中的变异策略引入到人工蜂群算法中,同时采用精英个体引导策略对雇佣蜂的搜索模式进行改进,如式(5)所示. (5) 式中:xbest为全局最优解,来自于外部精英解集;xr1,j和xr2,j为蜜源中随机选择的两个个体;F为缩放因子,F的值越小,算法跳出局部最优解的能力越强,但过小的缩放因子会导致收敛速度缓慢,影响算法的效率,F的值越大,有利于提高算法的开发能力,但是过大的F值会使算法陷入局部束缚.本文将当前蜜源与全局最优蜜源之间的欧氏距离作为F值,计算方法如式(6)所示,使算法在精英解的引导下能够根据个体与精英个体之间的相似度自适应地调整搜索范围的大小,从而提高算法的搜索效率. (6) 观察蜂通过雇佣蜂传来的信息,按照式(7)计算每个蜜源被选择的概率,用轮盘赌的方式选择具有一定的随机性. (7) 式中:fiti为第i个蜜源的适应度值. 信息熵能度量随机事件发生的不确定性,本文将信息熵引入到蜂群算法中,以信息熵值控制蜜源被选择的概率的大小.多目标的测试用例优先级排序问题属于离散的多目标优化问题,因此蜜源被选择的概率的信息熵计算如式(8)所示, (8) 借鉴信息冗余度衡量信息源的相关性程度的思想,本文定义蜜源相关性程度a,计算公式如式(9)所示, a=1-H/Hmax, (9) 式中:Hmax为最大熵值,即当pi=1/Dim时,Dim为所处理数据的维度.a的值越大表示蜜源与最优蜜源之间的相关性越小; 反之,蜜源与最优蜜源之间的相关性越大.为了提高算法跳出局部最优的能力,本文按照式(10)进行选择,从而提高与当前最优解相似度较小的解被选择的概率,以保证蜜源个体的多样性. (10) 回归测试旨在较短的时间内发现更多的软件错误,可以用软件缺陷检测率(Average Percentage of Fault Detect,APFD)作为度量准则.而在实际测试过程中,测试用例未执行之前,APFD的值未知,而一般情况下,测试用例对软件的语句、 分支、 块等的覆盖率越大,该用例能够发现软件中存在缺陷的概率就越大.因此,通常会用代码覆盖率代替APFD值作为优化目标,而将APFD值作为衡量优先级排序效果的准则.为了能让代码覆盖率较高且执行时间较短的测试用例优先执行,本文将平均语句覆盖率(Average Percentage of Statement Coverage, APSC)和有效执行时间(Effective Execution Time, EET)作为优化目标,计算方法如式(11)和(12)所示. (11) (12) 式中:N为测试用例的个数,M为程序语句的个数,TSi为覆盖程序语句i的第一个测试用例在序列中的位置,ETi为测试用例i的执行时间. 本文采用实数编码的方式,假设测试用例集TS中有N个测试用例,那么任意一个执行顺序可以表示为X={xr1,xr2,…,xrq,…,xrN},其中rq表示测试用例集TS中的第q个测试用例,xrq表示测试用例rq在测试用例集TS中的序号,且1≤xrq≤N.因此,测试用例集TS中所有测试用例的全排列组合构成了MOTCP问题的解空间. 输入: 搜索维度D,蜜源个数FN,最大开采次数Limit,算法最大迭代次数k,算法运行次数t. 输出: 满足Pareto最优解的个体. 根据D和FN,随机初始化得到一组包含FN个个体的可行解集M′,M′={X1,X2,…,Xi,…,XFN}. 根据式(11)和(12)评估已有的可行解,将评估为非劣解的可行解加入到外部精英集M; Do 在外部精英解集中按照式(3)选取全局最优解; If 开采次数 利用式(5)进行局部搜索,获得新蜜源; 根据式(11)和式(12)评价新蜜源; 采用算法1判断是否更新精英解集M; 利用式(8)~式(10)选择优质个体继续进行局部搜索; Else 放弃该蜜源,并利用式(1)随机生成一个新蜜源; 根据式(11)和式(12)对新蜜源进行评价; 采用算法1判断是否更新精英解集M; While(运行次数t<最大迭代次数k) 在外部精英解集M中挑选一个Pareto最优解,作为测试用例优先级排序的结果. 为了验证本文所提出MOABCO算法在收敛性和易陷入局部最优解这两个问题上改善的有效性,本文参考文献[12]选取了ZDT1、 ZDT2、 ZDT3函数进行测试,并在 MATLAB R2016b上编码实现,测试函数的信息如表 1 所示. 表 1 测试函数信息表 实验中,蜜源个数均为50,开采次数limit为100,最大迭代次数为1 000,维度D为30,精英解集大小为30,每次均独立运行10次,取平均值记录于表 2,括号内的数据是该指标对应的10次实验的方差值.本文选择逼近指标GD和分布指标SP作为比较两个算法的评价标准,GD和SP的值越小越好. 表 2 MOABC算法与MOABCO算法的对比结果 从表 2 的整体结果看,无论是GD还是SP,本文提出的MOABCO算法均优于基本的MOABC算法,说明本文的算法具有良好的求解性能. 为了进一步分析本文改进策略对算法的影响,针对ZDT2优化问题,将本文所提的MOABCO算法记为算法1,使用本文所提的选择策略的MOABC算法记为算法2,使用本文所提局部搜索策略的MOABC算法记为算法3,设定评价次数为1 000的条件下进行实验,3种算法的Pareto最优解的对比结果如图 1 所示. 图 1 不同多目标蜂群算法的Pareto最优解对比Fig.1 Comparison of Pareto optimal solution of different multi-object bee colony algorithm 从图 1 中可以看出,算法3产生的Pareto最优解在接近理论最优的程度上要优于算法2,证明了本文所提的局部搜索方法能够有效地对解空间进行开采.但正是因为全局最优个体引导的开采而导致解的多样性降低,在图 1 上表现出了聚集现象,而算法2的解则表现出分布均匀,证明了本文的选择策略能够有效保证算法运行过程中解的多样性.而多样性的增加导致Pareto最优解无法有效接近理论最优值.算法1在逼近理论最优和保持解的多样性上均表现良好,证明了本文所提的改进策略能够有效地避免算法早熟收敛和陷入局部最优解. 为了验证本文所提算法在解决MOTCP问题的有效性,分别将优化目标函数NSGA-II算法和MOABCO算法相结合,在Visual Studio 2015上采用C语言编程实现测试用例优先级排序,将本文提出的MOABCO算法与NSGA-II算法进行比较.本文选取了5个常用评测程序作为实验基准,基本信息如表 3 所示,这些基准程序被广泛应用于测试用例对软件缺陷检测能力的研究. 表 3 基准程序信息 实验中的每组实验数据均独立运行50次,取平均值记录,结果如图 2 所示.从图 2 中可以看出,随着程序规模的增大,NSGA-II和MOABCO算法所计算的APFD值均呈现下降趋势,但是MOABCO算法所计算的APFD值均优于NSGA-II算法,证明了由MOABCO算法进行的测试用例优先级排序的缺陷检测能力要优于NSGA-II算法. 图 2 MOABCO算法与NSGA-II算法针对不同程序计算的APFD值Fig.2 The APFD calculate value of different programs comparison among two algorithm 图 3 为PG5使用NSGA-II算法迭代300代和MOABCO算法迭代250代后算法运行30次时的Pareto解集分布.从图3中可以看出,MOABCO的Pareto解集中的个体分布更加均匀,分布范围更加广泛,且大多数个体均优于NSGA-II算法.证明了MOABCO算法可以加快种群的搜索速度,保证种群的多样性. 图 3 MOABCO算法和NSGA-II算法的Pareto解集的分布Fig.3 Distribution of Pareto solution sets of MOABCO algorithm and NSGA-II algorithm 文本针对基本MOABC算法存在的问题,改进了局部搜索策略、 蜜源的选择策略和外部精英解集及最优解更新策略,提高了算法的开采能力且增加了解的多样性,从而加快了算法的收敛速度,提升了算法的全局搜索能力.将MOABCO算法用于求解MOTCP问题中,相对于NSGA-II算法具有明显的优势.在今后的研究中,可以考虑增加优化目标的个数至3个及以上,以提升测试用例优先级排序的效率,降低回归测试用例的成本.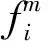
1.2 最优个体引导差分变异的局部搜索
1.3 基于信息熵的蜜源选择
2 基于MOABCO的多目标测试用例优先级排序
2.1 优化目标
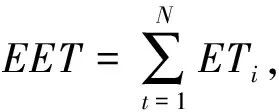
2.2 蜜源个体编码
2.3 MOABCO算法基本流程
3 实验结果分析





4 结束语

