叠片墙边界下土体结构应变破坏过程的模拟

，，

(福州大学土木工程学院， 福建福州350108)

0 引言

PFC是一种基于离散单元方法开发的用于模拟圆形颗粒介质的运动及其相互作用的数值分析程序[1-2]，近年来在岩土工程许多领域得到了初步的应用[3-4]。目前，PFC三轴试验模拟，在应力应变曲线数值拟合、细观参数对粗粒土宏观力学特性的影响分析等方面都表现出很大的优势[5-9]。

国内外学者运用PFC三轴数值试验得出了很多有价值的成果，例如：张志华[10]基于室内三轴试验研究成果，开展PFC三轴数值试验研究，提出了高效数值建模方法和新的细观分析方法，分析细观参数对宏观力学特性的影响，并进行了各细观参数力学及变形敏感性排序。陈亚东[11]根据确立的砂土细观参数,建立了桩基础的三维颗粒流数值分析模型,实现了桩基础荷载—沉降特性及桩周土体位移场的仿真模拟,且模拟结果与室内模型试验具有良好的一致性,验证了细观参数确定方法及结果的可靠性。Yoon[12]采用接触粘结模型研究了细观参数对材料的宏观力学特性的线性相关性。

然而，以上在PFC三轴模拟中，大都采用的刚性边界，而土体是一种柔性边界，从而无法正确模拟土样内部力链、孔隙率等的发展过程。叠片墙模拟方法，即是将单片墙体分为多层墙体，并分别对墙体施加速度，通过循环计算，墙体产生位移，调整其与内部土体颗粒的接触力，从而分别逐步达到目标围压[13]。在数值模拟中，边界条件的选择直接影响模拟结果的准确性，在叠片刚性墙体边界下，由于柔性墙以受力及径向位移实现，可以更准确的模拟土体结构应变破坏过程。

1 模拟分析过程

1.1 几何模型

土体在三轴模具内均以球状颗粒生成，以原状土孔隙率0.432 2按级配生成土样，颗粒单元在百万级。在PFC计算中，时间步长与最小半径有关，PFC的自动时间步长与颗粒最小粒径的R3/2成正比，过小的时间步长常常使计算步太多，因此可依据计算能力适当增大颗粒最小半径或者减小试样的尺寸来提高计算效率。

Q.Ni等(NI, Q, POWRIE W, ZHANG X, et al.Effect of Particle Properties on Soil Behavior: 3-D Numerical Modeling of Shearbox Tests[J]. 2000:58-70.)研究表明可将颗粒尺寸放大而不会影响到模拟结果。在本文研究中，对级配进行简化：(1)即将D<0.25 mm的颗粒均以0.25 mm计，土颗粒平均粒径为0.394 mm。(2)将颗粒半径进行放大5倍，即平均半径为0.975 mm。(3)并通过设定最大最小半径比Rmax/Rmin=2控制级配。

以往的研究中，通常以模型最小边长与颗粒平均半径比值(L/R)反映颗粒的分布结构。本文取L/R为40，最终生成直径39.1 mm高80 mm的圆柱形三轴模具。其模型主要参数见表1所示。

表1 模型参数Tab.1 Model parameters

1.2 边界设置

图1 PFC模具Fig.1 PFC mold

参考室内三轴试验，优化边界条件，并设置两种边界条件以便于对比。

传统方法以圆柱形模具进行PFC三轴模拟，如图1，其由两部分组成：依据伺服原理来保持围压一定的无摩擦侧边墙；应变控制提供轴向荷载的无摩擦上下刚性加载板。

在模拟中，侧边墙及加载板通常均以墙体生成，以往通过调整墙体刚度为球体刚度的1/10来达到柔性的目的。然而，在PFC中由于墙单元的刚性特征，得到的仍是刚性边界，从而也无法正确模拟土样内部力链、孔隙率等的发展过程。

在室内三轴试验过程中，土体一般用橡胶膜包裹，是一种柔性边界，并由水压提供稳定的围压。在模拟中，侧边界提供并控制围压的恒定，为模拟柔性边界，通常将颗粒串设置为侧边界。颗粒串是指在土样边界生成颗粒并赋予其一定接触，允许发生较大的侧向变形，以模拟橡胶模，这种颗粒串柔性边界多见于二维模拟中(G.Cheung等[14-15])。

在数值模拟中，边界条件的选择直接影响模拟结果的准确性，本文采用叠片墙的方法用到三轴模拟中来实现可变形边界(图2)，同时设立单片刚性墙体边界进行对比。

对于单片刚性墙，侧边墙体按传统方法刚度取为颗粒刚度的十分之一，以示柔性；而在叠片刚性墙体边界下，由于柔性墙以受力及径向位移实现，较大的刚度可以使墙体位移速度更加敏感，更易保持恒定的围压。因此，此处将叠片墙体侧边墙体刚度取与颗粒刚度一致，上下加载板刚度均取为颗粒刚度的十倍。

(a) 0 %应变模具形状 (b) 15 %应变模具形状

图2(a)将原单片墙体分为50片，分层伺服保证围压处于需求围压误差范围内，最后的形变结果与编写设定的程序及土体细观参数的选取有关，但从原理上已经实现可变形的柔性边界。

在数值模拟过程中，为维持围压的恒定，需要时刻监测侧墙受力，并据此伺服调整墙体径向速度来控制墙体围压。径向速度是实现叠片墙模拟的最重要一环，相比于单片墙，叠片墙的边界条件的实现存在以下特点与难点：

① 各片侧墙径向速度控制问题。

在一个时步内各片墙由约束运动引起的约束力最大增量是：

ΔFiw=kni(w)NciuiΔt,

(1)

其中：Nci为第i片侧墙上的接触数量；kni(w)为为第i片侧墙上的接触平均刚度；ui为第i片墙体的径向速度。

约束力增量引起的应力变量即为：

(2)

Ai=2π×ri×hi,

(3)

其中：Ai是第i片墙的约束面积，ri为第i片墙体的半径，hi第i片墙体的接触高度。

应力变量的绝对值必须小于测量值与需求值之间的差值。可以通过一个小于1.0的放大系数α表示，即：

|Δσi(w)|<α|Δσ|。

(4)

将式(2)代入式(4)中得到：

(5)

各片墙体的速度可由等式(6)表示：

ui=Gi(σmeasured-σrequired)=GiΔσ，

(6)

其中：Gi是各片侧墙的增量参数，Δσ围压测量值与控制值差值。

将式(6)代入式(5)，可得到G参数：

(7)

②Gi中各参数实时更新问题。在伺服中，提取当前片墙的ri、hi、kni(w)、Nci，得到墙体的当前速度Gi，迭代计算一定步数(此处为100步)；重新提取此时当前片墙Gi的各参数，并迭代计算；反复循环直到各片墙均达到预围压后可停止计算。

③ 对存在变化的侧墙接触高度实时更新、不变的侧墙接触高度进行固定可简化伺服过程、提高计算效率。侧墙在剪切过程中本身不存在压缩，但在上下加载板的作用下，其两端部分侧墙的接触高度存在变化。本次室内试验土样均于15 %轴向应变前即产生破坏，因此将50片侧墙从底部进行编号，则接触高度存在变化的仅有1～4号及47～50号墙体，5～46号墙体接触高度始终不变，将其固定减少程序的识别可提高计算效率。

③ 加载速度选取问题。加载速度的选取影响着颗粒的横向运动，最终对叠片墙横向变形产生较大影响，需要通过试算选取最优加载速度。

2 应变破坏过程分析

2.1 100 kPa围压土体应变过程分析

2.1.1 位移矢量

本文过试样中心沿x轴取一个垂直于上下加载板的剖面，将位于其上及前的颗粒位移云图提取如下：

图3是不同轴应变下颗粒位移矢量云图，图中线条的粗细代表位移的大小，位移越大线条越粗。观察分析轴应变在2 %、4 %、6 %、8 %、12 %、15 %处的颗粒位移场发现，压缩进行时由于上下层对称加载板的运动，模型上下层颗粒集体向中运动，中间层颗粒向四周运动。在轴应变为2 %～4 %时，模型颗粒位移主要表现为上下两层的轴向位移，而中间部分径向细条非常细，代表横向位移非常小，边界并无明显变形；从6 %开始，随着轴应变的增大横向变形逐渐增大，结合应力应变曲线可知，这与应力峰值一般在轴应变为5 %～6 %相吻合，说明当达到应力应变峰值之后，试样结构产生破坏并逐渐累积发展。对于叠片墙边界，在对称加载下，PFC试样表现为中间明显鼓胀的效果。

图3 不同轴应变下颗粒位移矢量云图(100 kPa)Fig.3 Particle displacement vector cloud diagram under different axis strain (100 kPa)

2.1.2 接触力链

根据对接触的赋予方式，此处可以通过提取不同应变时的接触粘接的分布情况，进而研究试样的破坏过程。

图4是不同轴应变下接触粘结力链，图中上下及四周的线段代表加载板及50片墙体，黑色线段代表压力，红色的则代表拉力，线条的粗细反应其传递荷载的大小。由图4可见：压力接触力链与拉力接触力链在试样内部均有分布，压力接触力链占主要部分，轴向分布。其受到的荷载比拉力要大，拉应力则主要呈水平分布；当位于2 %～6 %应变时，随着轴应变的增大，压力链逐渐变粗，且基本平行于主应力方向，试样主要呈轴向变形；当位于6 %～15 %应变时，力链逐渐变细，压应力链由竖直逐渐倾斜，试样横向变形增大；当为15 %应变时，可以明显看出图中有个带状空白区，表明此处的接触粘接消失，转换成为线性接触模型。

图4 不同轴应变下接触粘结力链(100 kPa)Fig.4 Contact adhesion chain under different strains (100 kPa)

值得注意的是，上图中的力链仅显示的是接触模型为接触粘结的力链，未显示新生成的线性接触。通过对应变过程中接触粘结断裂而新生成的线性接触数目进行统计，见表2：

表2 新生成的线性接触数目Tab.2 Number of newly generated linear contacts

从表2中可见，当轴向应变为2 %～4 %时，新生成的线性接触数目很少，表明粘结基本无断裂，土体基本处于弹性阶段；在应变为4 %～6 %之间时，断裂数目有明显的增大，结合应力应变曲线，发现峰值也位于该应变范围。表明土体达到抗剪强度峰值后，土体开始破坏，塑性变形出现并逐渐发展；在应变为6 %～15 %时，接触断裂逐渐发展，最终的断裂占整体接触数目的7.8 %。

依据应力应变关系，颗粒间应变位移及接触粘接力链，可将土的破坏过程分为三部分：

① 弹性变形阶段。试样在弹性阶段的前期时，试样内颗粒间接触力由上下层向中间逐渐增大，方向基本平行于主应力方向，基本不存在接触粘结断裂；在压力作用下颗粒主要呈轴向运动，压缩变形主要来源于材料内部颗粒间孔隙率的降低，其中上下层孔隙率变小幅度大于中间层，试样整体基本不呈现横向变形；该阶段的应力—应变曲线主要呈线性增长。

② 塑性发展及强度峰值阶段。弹性变形结束之后，继续增加的荷载使颗粒间接触力增大，达到颗粒间接触粘结强度并开始发生破坏，新的接触模型开始产生和扩展；从孔隙率时程变化上看，孔隙率也随峰值应变而达到最密点，并开始提升；随着颗粒间粘接断裂，应力应变曲线出现塑性变形并达到峰值，横向应变开始变大。

③ 峰后破坏阶段。峰后颗粒间接触力逐渐变小，表征峰后应力逐渐降低；粘结破坏数速率增大，并逐渐发展，最终形成一个明显的断裂面；对孔隙率监测显示，产生横向变形的土层，其孔隙率增速最大；峰后阶段的压力链，开始倾斜，基本垂直于颗粒位移方向，即横向应变速率大于轴向应变，试样最终出现明显的横向变形。

2.2 150 kPa、200 kPa围压土体应变过程分析

2.2.1 位移矢量云图

各围压下颗粒位移矢量云图，见图5、6所示。

从图5及6中可见，150及200 kPa围压下，2 %～4 %轴应变时模型中颗粒位移与100 kPa围压时一致，均为上下层向中间移动，中间部分横向移动，主要为轴向的位移，基本不出现横向位移；相较于100 kPa围压，150 kPa及200 kPa围压中试样土体颗粒主要表现为轴向位移，随围压的增大而产生的横向变形则表现为越来越迟，依据应力应变曲线，抗剪强度峰值在应变为4 %～6 %之间出现。当轴向应变为8 %时，150及200 kPa的横向变形仍很小，通过软件得到边界墙体半径的大小显示试样最终形成的横向变形也要较100 kPa小。

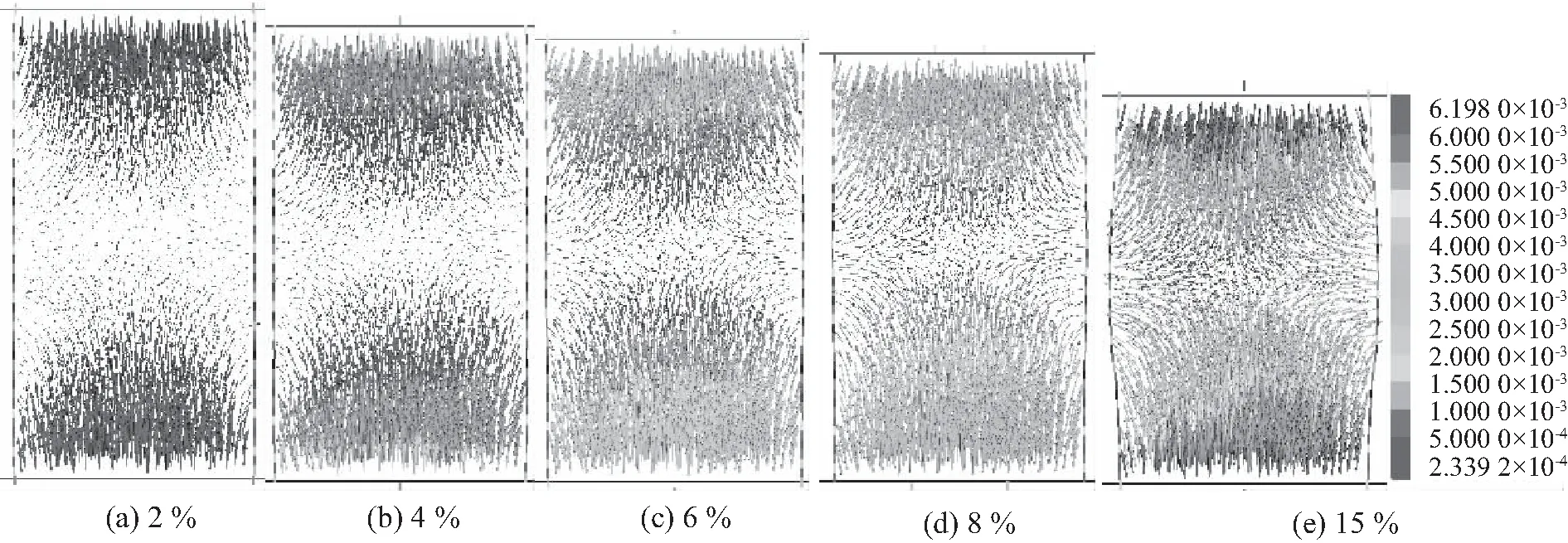
图5 不同轴应变下颗粒位移矢量云图(150 kPa)Fig.5 Particle displacement vector cloud map under different axis strain (150 kPa)

2.2.2 接触力链

各围压下试样接触力链见图7、8所示。

图7 不同轴应变下接触粘结力链(100 kPa)Fig.7 Contact adhesion chain under different strains (100 kPa)

由图7、8可见：当围压为150 kPa及200 kPa时，接触力较100 kPa围压时明显较密，处于峰值应变之前时，随着轴应变的增大，力链逐渐变粗，且基本平行于主应力方向，试样主要呈轴向变形，峰值之后接触粘接断裂产生新的刚性接触，接触力链逐渐变细，横向变形出现并逐渐发展；通过对接触粘结断裂而新生成的线性接触数目的统计，线性接触生成规律与100 kPa围压时相同，但数目更多，达到15 %应变时，150 kPa及200 kPa围压中最终断裂占整体接触数目的8.2 %及8.5 %，这表明高围压下即使试样内部颗粒之间的接触网络产生大量破坏，横向变形大，颗粒间仍存在较大的接触力，即表现为存在较高的残余强度。

3 结论

① 相较于单片墙边界，叠片墙边界可以实现三轴模拟中试样的横向变形，从而精确地描述试样内部颗粒位移、局部孔隙率、局部应力变化以及土体结构破坏的演变过程。

② 土的破坏过程可分为三部分：弹性变形阶段，接触力由上下层向中层逐渐增大，试样整体基本不呈现横向变形。压缩变形主要来源于材料内部颗粒间孔隙率的降低，不存在接触粘结断裂；塑性发展及强度峰值阶段，颗粒间应力达到粘结强度开始发生破坏，新的接触模型开始产生和扩展、应力应变曲线出现塑性变形并达到峰值，横向应变开始变大；峰后破坏阶段，颗粒间接触力逐渐变小，粘结破坏数速率增大，最终形成一个明显的断裂区域，并出现明显的横向变形。

③ 高围压下颗粒主要表现为轴向位移，随围压的增大而产生的横向变形出现迟滞的现象，且最终出现的横向变形也更小。抗剪强度峰值在应变为4 %～6 %之间出现。

④ 即使高围压下试样内部颗粒之间的接触网络产生大量破坏，横向变形大，颗粒间仍存在较大的接触力，即表现为存在较高的残余强度。