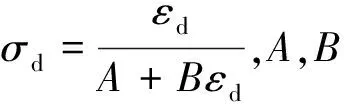干湿循环下红粘土动力特性试验研究

，

(贵州大学土木工程学院， 贵州贵阳550025)

0 引言

在土动三轴试验分析中，土的动剪切模量和动阻尼比是其重要的参数。动剪切模量反映了路基土体动剪应力与动剪应变之间的关系，它是连接应力和应变的纽带，无论在理论分析还是数值计算中，土体模量参数都具有非常重要的意义。而动阻尼比则反映了路基土体应力—应变关系的滞后性，也反映了土体中能量衰减的规律。目前，关于小应变幅值条件下动三轴研究多集中于砂土、膨胀土及改良土。小应变幅值条件下，对特殊土动力特性的研究相对较少[1-3]。刘晓红针对高速交通循环荷载下红粘土路堑基床的动力稳定性问题，基于大量室内动三轴试验，研究了不同试验条件下原状结构红粘土动本构关系及动模量衰减规律[4]。李剑为进一步揭示应力历史对红黏土动力特性的影响，将重塑红黏土土样在承受不同应力历史条件下进行动三轴试验，分析了不同应力历史对重塑红黏土的影响规律[5]。罗丹鹏运用数理统计方法研究广西区内189个红粘土样品自振柱试验成果，发现广西红粘土动剪切模量比中应变范围变易性大，阻尼比变异性无明显规律[6]。穆坤等针对广西上林县原状红黏土开展一系列循环加载动三轴试验，分析天然含水率、围压与固结应力比等对红黏土动力特性[7]。王勇通过对取自桂林红粘土进行 GDS 动三轴试验，提出确定土体的动剪切模量和阻尼比[8]。上述研究都未考虑干湿循环的影响。红粘土作为一种特殊性土，在自然条件下，经过反复失水收缩、吸水饱和膨胀，导致土体结构发生变化，引起红粘土力学特性降低，最终引起边坡坍塌、路基失稳等工程破坏。近期对干湿循环条件下土体力学特性的研究较多。但大部分学者都是关于干湿循环对静力特性影响的研究[9-15]。因此，有必要开展干湿循环条件下红粘土动三轴试验，研究红粘土动力特性对工程稳定性分析有很好的指导意义。本文主要针对贵阳地区红粘土，研究了在不同干湿循环路径下红粘土动力特性试验参数变化规律以及动应力与动应变的本构关系。

1 红粘土基本物理性质

本次试验所采用的红粘土取自贵州大学二期工程图书馆附近某基坑处，取土深度在地表下5 m左右。土料特征为：黄褐色及棕红色为主，级配良好，为不均匀土，有少量植物根尖及小石子，结构致密，天然含水率较高，土样潮湿。基本物理指标见表1[16]。

表1 红粘土基本物理指标Tab.1 Physical indexes ofred clay

2 试验方案

2.1 样品制备

采用静力压实制备压实度为85 %和93 %，含水率为20 %三轴试样，直径3.91 cm，高8 cm。

2.2 干湿循环试验

① 先干后湿试验

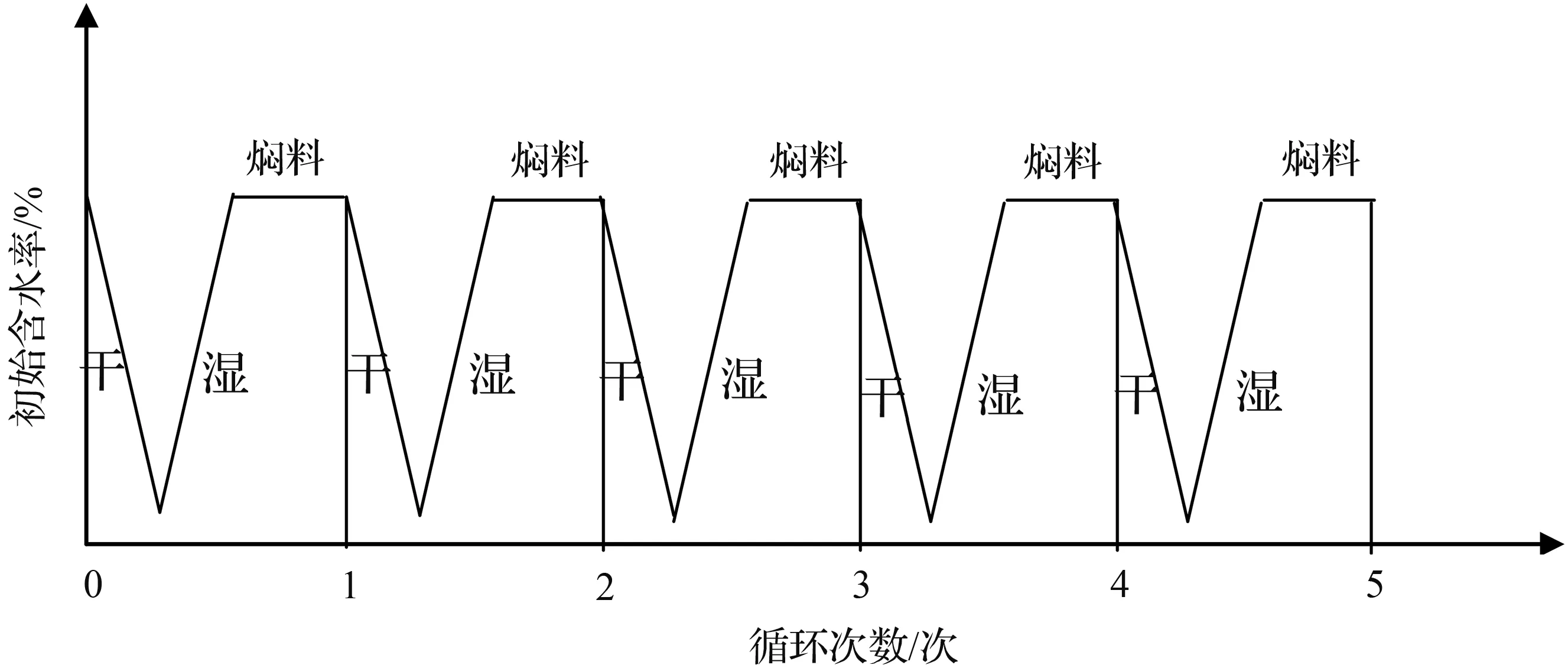
图1 先干后湿试验方法Fig.1 Dry first and then wet test method

初始含水率：为最佳含水率20 %。干：温度分别控制在105 ℃和25 ℃连续烘干直至恒重。湿：烘干后的样品加水到初始含水率20 %。焖料：为使水分均匀渗透，将样品在保湿缸保湿24 h，此完成一次干湿循环试验。用类似方法完成2、3、4、5次干湿循环试验。

② 先湿后干试验

图2 先湿后干试验方法Fig.2 Wet first and then dry test method

初始含水率：为最佳含水率20 %。湿：根据文献[17]和文献[18]，在道路的运营初期(3～5 a)，路基的含水率将由最佳含水率(optimal moisture content，OMC)逐渐增大至平衡含水量(equilibrium moisture content，EMC)，并随着运营期的增长，路基内部含水率始终在EMC附近波动。LTPP(Long-term pavement performance program)针对运营期道路路基含水率展开现场调查，在137处调查中有59处为粘性土，粘性路基土实际含水率都大于最佳含水率，含水率处于ωop～ωop+7 %之间[10]。本次试验样品最佳含水率为20 %，根据相关文献资料并考虑最不利情况，样品增湿含水率为40 %。焖料：将样品在保湿缸保湿24 h。干：温度控制在105 ℃和25 ℃连续烘干直至含水率为初始含水率停止烘干，完成一次干湿循环试验。用类似方法完成2、3、4、5次干湿循环试验。

2.3 动三轴试验

试验采用西安力创材料检测技术有限公司制造的SDT-20型动态三轴测试系统，该系统可提供最大轴向激振动态荷载为20 kN，平均荷载波动度优于0.5 %，荷载振幅波动度优于2 %，变形精度优于0.5 %，量程为20 mm，应变测量精度可达10-4，三轴压力室承受最大围压为1 MPa，试验波形可选择正弦波、三角波、方波、梯形波、斜波等波形，可提供轴向、侧向激振频率范围为0～20 Hz。动力学试验参数见表1。

(a) 加荷系统

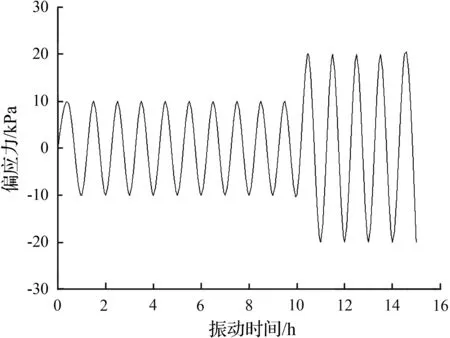
(b) 荷载波形图

3 试验结果

3.1 干湿循环下动力特性试验参数变化规律

由图4、图5和图6可知：

① 红粘土在干湿循环和周期振动荷载作用下的动应力—动应变关系具有明显的非线性关系，表现为强硬化型。动应力水平较低时，本构关系曲线较陡，土体处于弹性阶段；随着动应力幅值的逐渐增大，动本构关系曲线趋于平缓，土体处于弹塑性发展阶段。

② 动弹性模量、动剪切模量随应变的增大而降低，最终趋于平缓。同一动应变下，先湿后干比先干后湿的动弹性模量、动剪切模量更大。

③ 动阻尼比随动应变的增加整体呈现非线性增大的趋势，同一动应变下，先湿后干比先干后湿阻尼比更小。

④ 动弹性模量、动剪切模量随循环次数增加而降低，动阻尼比随循环次数的增加逐渐增大，且第1、2次循环降低幅度比较大；第3、4、5次降低幅度比较小，最终趋于平缓。试验红粘土土体的最大动阻尼比大多在10 %～20 %之间。

⑤ 常温(25 ℃)下干湿循环的动弹性模量、动剪切模量比高温(105 ℃)下干湿循环要大，动阻尼比要小。

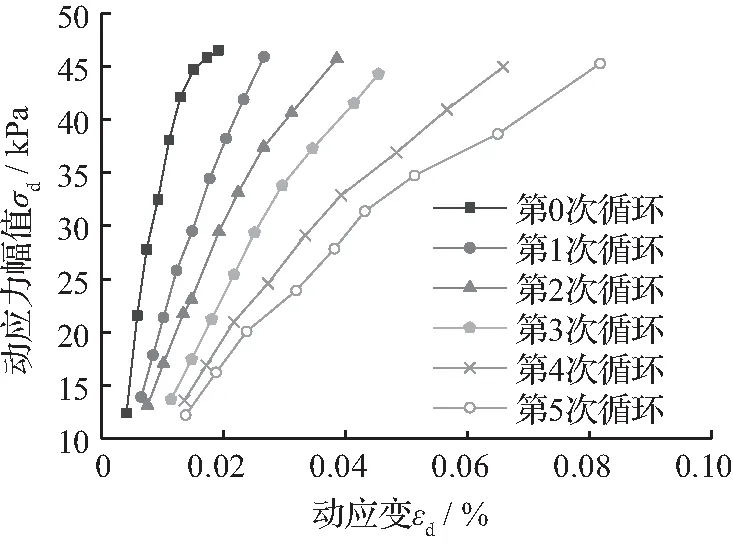
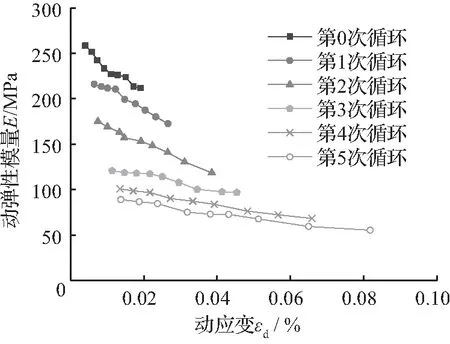
图4先干后湿下动力参数与应变关系(压实度K=85%)
Fig.4Kineticparametersandstrainrelationsunderdryfirstandthenwet(K=85%)

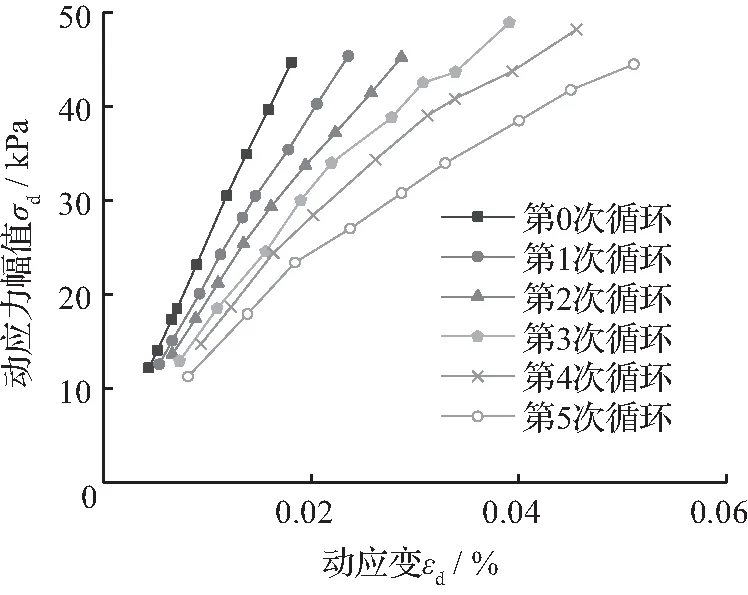
图5先湿后干下动力参数与应变关系(压实度K=93%)
Fig.5Kineticparametersandstrainrelationsunderwetfirstandthendry(K=93%)

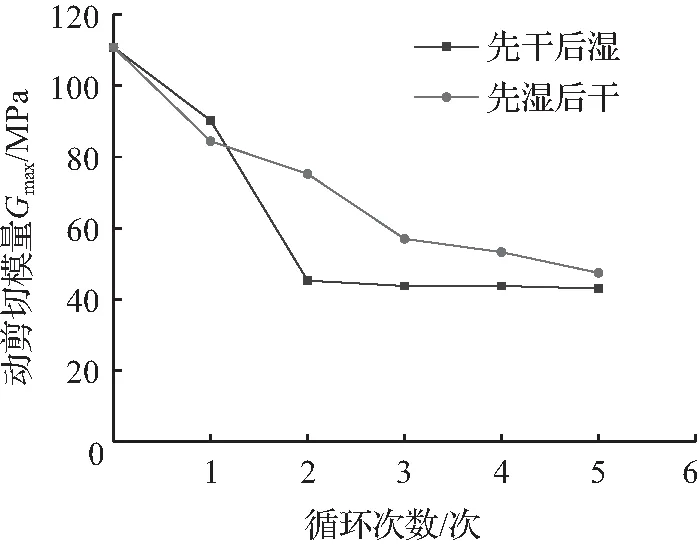
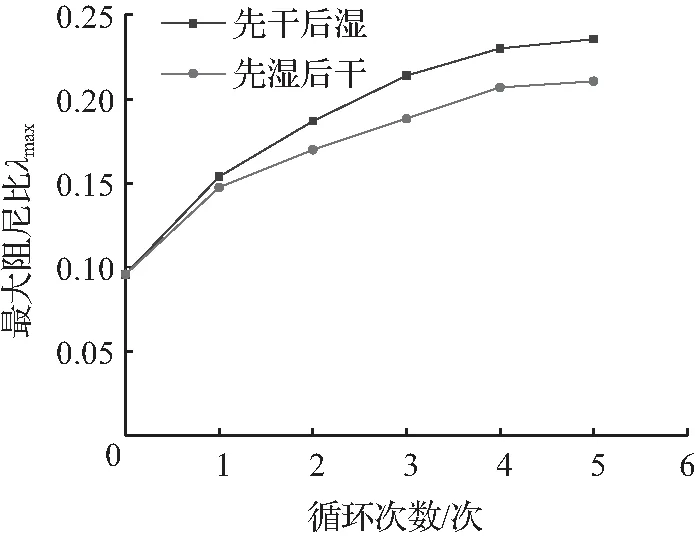
3.2 干湿循环下红粘土动本构关系

目前土的动本构模型有很多，可归纳为黏弹性、弹塑性和内时动本构模型等3类。这些本构模型用不同的方法，从不同的角度给出了动应力—应变关系定量计算方法。以往研究提出过很多动应力—应变关系的方程，如Hardin和Drnevich[19]提出的H-D模型，Stokoe(STOKOE K H, DARENDELI M B, ANDRUS R D， et al.Dynamic soil properties: laboratory，field and correlation studies[A]/ /Proc，2nd Int Conf on Earthquake Geotechnical Engineering,Vol.3,Lisbon,Portugal: 811-845)给出的修正双参数双曲线模型以及Martin和Seed[20]提出的Davidenkov模型。采用Origin8.0软件对动应力—动应变关系图进行拟合，部分结果如下图表。

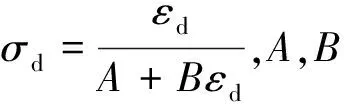
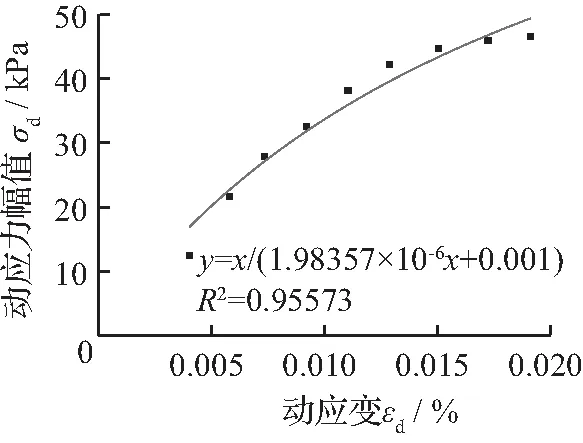
(a) 第0次循环(b) 第1次循环(c) 第2次循环

(d) 第3次循环(e) 第4次循环(f) 第5次循环

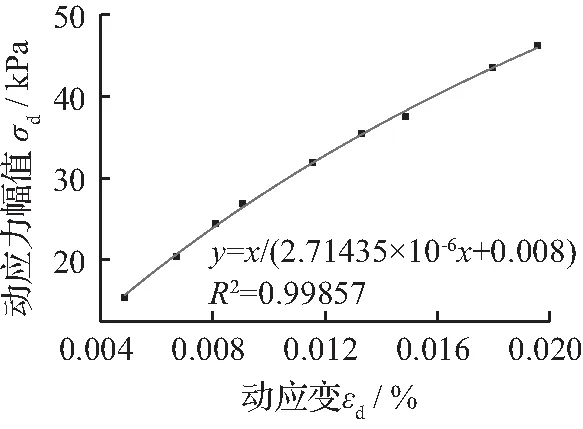
(a) 第0次循环(b) 第1次循环(c) 第2次循环

(d) 第3次循环(e) 第4次循环(f) 第5次循环

(a) 第0次循环(b) 第1次循环(c) 第2次循环

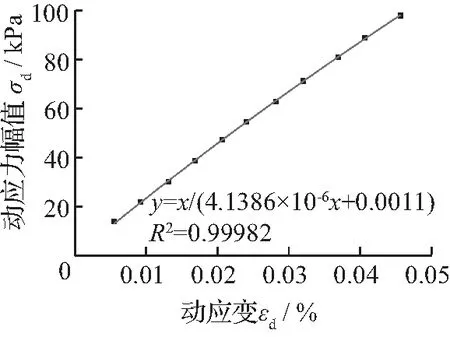
(d) 第3次循环(e) 第4次循环(f) 第5次循环

循环次数/次含水率/%压实度/%围压/kPa固结比频率/HzABR2120931002003001.513×10-60.004 20.980 23×10-60.003 50.980 33×10-60.002 30.976 9220931002003001.519×10-60.005 90.978 17×10-60.001 70.973 15×10-60.001 80.974 9320931002003001.518×10-60.004 10.981 36×10-60.005 40.990 25×10-60.003 10.986 2420931002003001.518×10-60.004 30.970 66×10-60.002 80.988 35×10-60.002 10.962 7520931002003001.518×10-60.004 50.984 97×10-60.002 90.976 16×10-60.002 70.993 7

表4 高温先湿后干循环试验红粘土双曲线模型参数Tab.4 High temperaturethe wet first and then dry test red clay hyperbolic model parameters

4 结论

① 红粘土在干湿循环和周期振动荷载作用下的动应力—动应变关系具有明显的非线性关系，表现为强硬化型。动应力水平较低时，本构关系曲线较陡，土体处于弹性阶段；随着动应力幅值的逐渐增大，动本构关系曲线趋于平缓，土体处于弹塑性发展阶段。

② 动弹性模量、动剪切模量随应变的增大而降低，动阻尼比随动应变的增加而增大，最终趋于平缓。同一动应变下，先湿后干比先干后湿的动弹性模量、动剪切模量要大，动阻尼比要小。常温(25 ℃)下干湿循环的动弹性模量、动剪切模量比高温(105 ℃)下干湿循环要大，动阻尼比要小。

③ 动弹性模量、动剪切模量随循环次数增加而降低，动阻尼比随循环次数的增加逐渐增大，且第1、2次循环降低幅度比较大；第3、4、5次降低幅度比较小。试验红粘土土体的最大动阻尼比在10 %～20 %之间。