单自由度Maxwell阻尼器耗能结构基于频响函数谱矩的等效阻尼

，，

(1.广西大学土木建筑工程学院， 广西南宁530004；2.广西科技大学土木建筑工程学院， 广西柳州545006)

0 引言

粘滞及粘弹性耗能结构广泛应用于实际工程的抗震被动控制[1-3]。对于粘弹性耗能结构，目前国内外普遍采用基于反应谱的抗震设计方法[4-8]，故合理确定其等效阻尼是进行抗震设计的关键环节[9-11]。

Maxwell模型阻尼器本构方程简便，物理意义明确，易于扩阶分析，模型计算参数易于从试验数据拟合[5-6],一般线性流体阻尼器满足Maxwell模型[12-14]，实际工程大量应用的支撑—粘滞阻尼器复合系统也可用Maxwell模型精确建模[15-17]，且一般粘弹性阻尼器也可用Maxwell模型近似表示[7]或用广义Maxwell模型表示[18,19]，故研究Maxwell阻尼器耗能结构的等效阻尼具有理论和工程意义。

目前研究粘弹性耗能结构等效阻尼的最主要方法是模态应变能法[5-11]，国内外已利用该方法建立了粘弹性耗能结构振型分解反应谱抗震设计方法。此外，还有取结构基频的强行振型解耦法[20]、复模量分析法[21]、随机平均法[22,23]和多尺度法[24]等，但它们均为一阶近似方法，其精度和适用范围有待提高。

一般线性粘弹性耗能结构的动力响应特性完全由其频率响应函数确定[8]。对减震工程实际应用的Maxwell流体阻尼器，其松弛时间λ=0.006 s[5]或λ=0.014 s[12],故λ是一个很小的参量；对于实际工程大量应用的支撑—粘滞阻尼器复合系统，为保证复合阻尼器系统充分发挥减震效果，我国抗震规范要求[4]：ω0λ≤1/3(ω0为结构基频)，因此，其松弛时间λ也是一个较小的参量。

基于以上两点性质，本文重构此类耗能结构的基本分析方程，并基于频率响应函数的零阶及二阶谱矩完全相同的等效准则，获得单自由度Maxwell耗能结构的等效阻尼和等效频率的近似解析式，使其精度优于经典的模态应变能法所得结果，并为今后耗能结构基于零阶、一阶和二阶谱矩完全相同的更高精度等效阻尼分析奠定基础。

1 运动方程

对于图1 所示的单自由度Maxwell阻尼器或支撑—粘滞阻尼器复合系统减震结构，

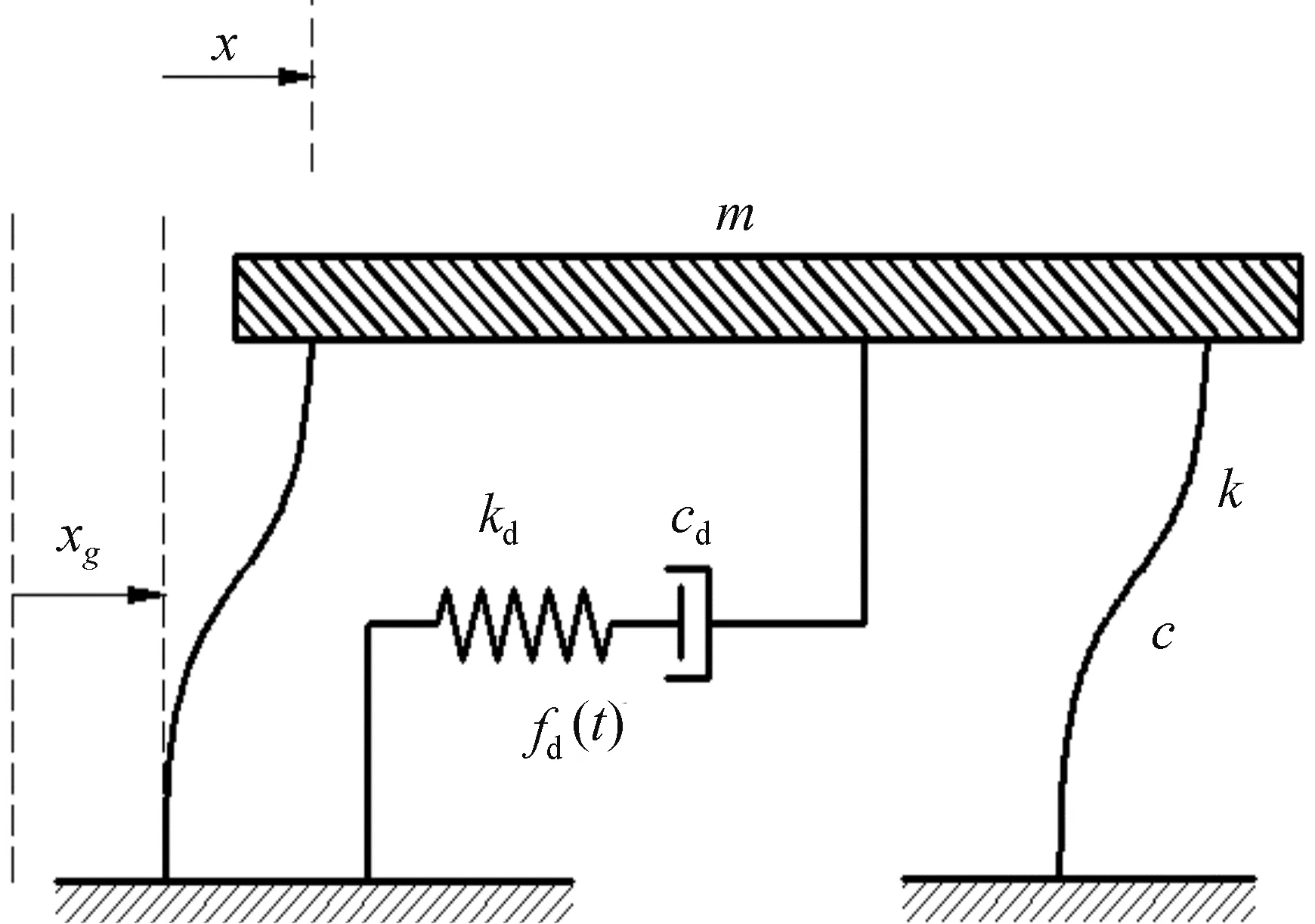
图1 结构计算简图Fig.1 calculation diagram of the structure

在地震激励下，其运动方程可化简为[24]：

(1)

(2)

式中：

(3)

作恒等变换：

(4)

式中：pb为一新变量。

则方程(1)和(2)可转化为：

(5)

(6)

式中：

(7)

文献[24]研究表明：当松弛时间λ为小量时，采用方程(5)和(6)作为等效阻尼的基本分析方程，其分析精度优于方程(1)和(2)。

2 结构频响函数及其谱矩

对方程(5)及(6)取傅氏变换，经简化可得：

(8)

(9)

利用随机振动分析的James积分公式[25],可求得频率响应函数Hx(iω)的零阶和二阶谱矩I0、I2解析式分别为：

(10)

(11)

3 基于谱矩的等效阻尼和频率

3.1 等效系统的频率响应函数及谱矩

假设结构系统(5)及(6)的等效系统为：

(12)

式中：ωe、ξe分别为结构待定的等效频率及等效阻尼比。

对方程(12)取傅氏变换，可得：

(13)

(14)

式中：Hxe(iω)为等效结构位移频率响应函数。

同理，等效系统的频响函数Hxe(iω)的零阶和二阶谱矩I0e、I2e的解析式分别为：

(15)

(16)

3.2 基于谱矩的等效频率和阻尼

由方程(8)及(13)可以看出，结构系统(5)和(6)以及等效系统(12)的动力响应特性完全由它们所对应的频响函数Hx(iω)和Hxe(iω)确定。

显然，如果Hx(iω)=Hxe(iω)，也即Hx(iω)和Hxe(iω)的各阶谱矩均相等，则结构系统(5)和(6)与其等效系统(12)完全等效；如果Hx(iω)和Hxe(iω)的有限阶谱矩相等，则结构系统与其等效系统近似等效，显然，有限阶谱矩相同的个数越多，则等效精度越高。

为此，本文提出零阶和二阶谱矩相同的近似等效准则，来确定待定的等效频率和阻尼，也即：

I0e=I0；I2e=I2。

(17)

基于上述等效准则，由式(15)和(16)以及式(10)和(11)，可求得结构的等效频率和阻尼分别为：

(18)

(19)

至此，已获得了结构系统基于零阶和二阶矩完全相同的等效阻尼和等效频率的解析式。显然，为进一步提高等效精度，可采用零阶、一阶和二阶谱矩均相同的等效准则。此时，等效系统(12)的等效参数γ=γe应作为待定参数，并利用等效条件求解。

3.3 Maxwell阻尼器的等效系统

由于耗能结构的安全性取决于结构构件和Maxwell阻尼器的安全性，为对Maxwell阻尼器进行抗震设计，建立其等效系统是必要的。

由方程(5)及(12)，可得：

(20)

由式(20)及(3)和(4)，可得阻尼器的等效系统为：

(21)

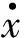
4 近似等效系统的精度分析

4.1 频率响应函数对比分析

单自由度Maxwell阻尼原始耗能结构系统(1)及(2)的频率响应函数精确解为：

(22)

对于原始结构系统(1)和(2)，基于频响函数零阶和二阶谱矩相同所获得的近似频响函数的解析式为：

(23)

对于原始结构系统(1)和(2)，由模态应变能方法[5-11]所得近似等效系统为：

(24)

式中：

(25)

相应的近似频率响应函数解析式为：

(26)

显然，将上述两种近似方法所得的频响函数近似解与精确解进行比较，可分析两种近似方法的计算精度。

4.2 非平稳响应方差精度对比分析

4.2.1 非平稳地震激励模型

(27)

(28)

(29)

式中：E(·)表示取数学期望值；S0为地震谱强度；δ(·)为狄拉克函数；I(t)=2πa2(t)为调制强度函数。

4.2.2 近似等效系统的非平稳响应方差

本文方法和模态应变能法所获得的近似等效系统(12)及(24)可统一表示为：

(30)

作复模态变换：

(31)

则方程(30)可解耦为：

(32)

(33)

由式(31)、(33)及(29)，近似系统位移x(t)的非平稳响应方差为：

(34)

(35)

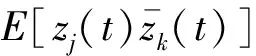
① 阶跃型调制强度函数

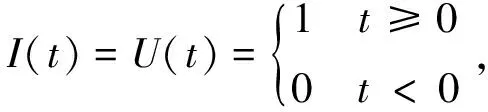
(36)

(37)

② Shinozuka-Sato型调幅函数[27]

A(t)=U(t)(e-a1t-e-a2t),

(38)

I(t)=2πU2(t)(e-a1t-e-a2t)2,

(39)

式中：a1、a2为常数。

(40)

③ 分段连续型调制强度函数[28]

(41)

式中：I0、c、t1、t2均为常数。

(42)

(43)

(44)

④ 余弦型调制强度函数[29]

I(t)=U(t)(c+dcosΩt),

(45)

式中：c、d、Ω为常数。

(46)

4.2.3 原始结构系统非平稳响应方差

对于原始结构系统(1)和(2)，在上述4种经典非平稳均匀调幅白噪声地震激励下，结构位移非平稳响应方差E[x2(t)]的解析解已由文献[30]给出。

显然，将上述两种近似方法所得的结构非平稳响应方差近似解与精确解进行比较，可以分析两种近似方法的计算精度。

4.3 算例分析

4.3.1 频率响应函数算例分析

对于工程实际应用的Maxwell流体阻尼器，其松弛时间通常为0.006 s[5]或0.014 s[12]；对于实际工程应用的支撑—粘滞阻尼器复合系统，我国抗震规范要求ω0λ≤1/3，且由阻尼器提供的附加阻尼比不宜超过20 %。由于实际工程中，绝大多数单自由度结构自振频率范围为：10 rad/s≤ω0≤30 rad/s，结构固有阻尼比ξ0=0.05；故取下列3组典型的实际工程参数进行算例分析，cb=2βω0，其中β为形式阻尼比。

①ω0λ=1/3，β=0.2；自振频率ω0分别取10、20、30 rad/s；其频响函数模的对比曲线示于图2至图4。从图中可以看到：在单自由度结构的频率范围内，本文方法精度较经典的模态应变能方法有较大提高。

图2频响函数|H(iω)|计算值
Fig.2Calculatedvaluesof|H(iω)|

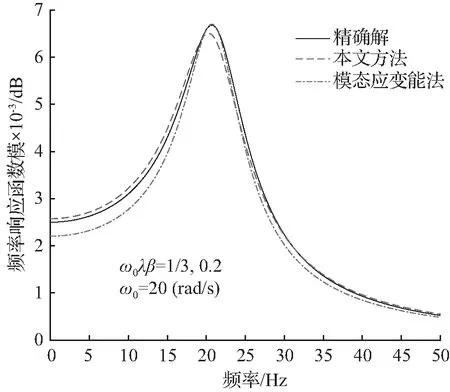
图3频响函数|H(iω)|计算值
Fig.3Calculatedvaluesof|H(iω)|

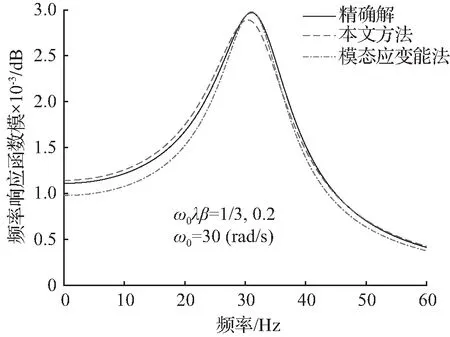
图4 频响函数|H(iω)|计算值Fig.4 Calculated values of |H(iω)|

② 当ω0=15 rad/s，β=0.2；ω0λ分别取1/4和1/3；其频响函数模的对比曲线示于图5至图6。从图中可以看到：随着参数ω0λ增大，本文方法精度有所下降，但在我国抗震规范要求的参数范围内，本文方法精度较经典的模态应变能方法有较大提高。

图5频响函数|H(iω)|计算值
Fig.5Calculatedvaluesof|H(iω)|

图6频响函数|H(iω)|计算值
Fig.6Calculatedvaluesof|H(iω)|

③ 当ω0=15 rad/s，ω0λ=1/3；β分别取0.15及0.25；其频响函数模的对比曲线示于图7至图8。从图中可以看到：随着阻尼器形式阻尼比β的增大，本文方法精度有所下降，但在我国抗震规范要求的附加阻尼比不大于20 %的参数范围内，本文所求的等效阻尼精度较经典模态应变能方法有较大提高。

图7频响函数|H(iω)|计算值
Fig.7Calculatedvaluesof|H(iω)|

图8频响函数|H(iω)|计算值
Fig.8Calculatedvaluesof|H(iω)|

4.3.2 非平稳响应方差算例分析

取下列4组典型工程参数进行结构位移非平稳响应方差分析：结构自振频率ω0=20 rad/s；固有阻尼比ξ0=0.05；ω0λ=1/3；地震谱强度S0=0.030 6 m2/s3。

① 对于阶跃型调制强度函数，分别取β=0.1和0.2；其非平稳位移响应方差的对比曲线如图9和图10所示。

② 对于Shinozuka-Sato型调幅函数，α1=0.5 s-1；α2=1 s-1；分别取β=0.1和0.2；其非平稳位移响应方差的对比曲线如图11和图12所示。

③ 对于分段连续型调制强度函数，c=0.18 s-1；I0=1，t1=3 s，t2=13 s； 分别取β=0.1和0.2；其非平稳位移响应方差的对比曲线如图13和图14所示。

图9跃阶型调制强度激励的位移响应方差
Fig.9ResponsevarianceofdisplacementunderStepexcitation

图10跃阶型调制强度激励的位移响应方差
Fig.10ResponsevarianceofdisplacementunderStepexcitation

图11Shinozuka-Sato型调幅激励下的位移响应方差
Fig.11ResponsevarianceofdisplacementunderexcitationofShinozuka-Satotype

图12Shinozuka-Sato型调幅激励下的位移响应方差
Fig.12ResponsevarianceofdispalcementunderexcitationofShinozuka-Satotype

图13分段连续型调制强度激励下的位移响应方差
Fig.13ResponsevarianceofdisplacementunderPiecewisecontinuousexcitation

图14分段连续型调制强度激励下的位移响应方差
Fig.14ResponsevarianceofdisplacementunderPiecewisecontinuousexcitation

④ 对于余弦型调制强度函数，c=1；d=1；Ω=π/16 rad/s；分别取β=0.1和0.2；其非平稳位移响应方差的对比曲线如图15和图16所示。

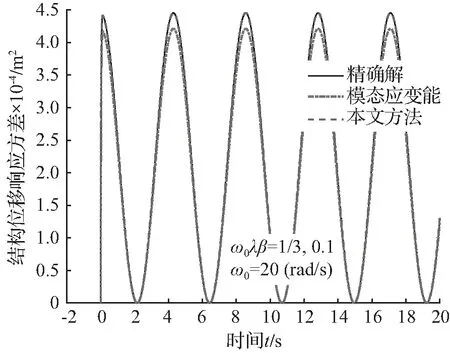
图15余弦型调制强度激励下的位移响应方差
Fig.15Responsevarianceofdisplacementundercosinenoiseexcitation

图16余弦型调制强度激励下的位移响应方差
Fig.16Responsevarianceofdisplacementundercosineexcitation

从图9至图16可看出：对于4种调幅函数，本文方法近似解与精确解基本吻合，且对附加阻尼比β的变化不敏感；而模态应变能方法近似解则误差较大，且随着附加阻尼比β的增大而增大。显然本文方法的精度明显优于模态应变能方法。

5 结论

为建立Maxwell流体阻尼器和支撑—粘滞阻尼器复合系统减震结构基于反应谱的抗震设计方法，对单自由度Maxwell耗能结构的等效阻尼及频率的近似解析解进行了研究，结论如下：

① 基于耗能结构动力响应特性完全由其频响函数确定的性质，采用频响函数有限阶谱矩相同的等效准则，可以获得单自由度Maxwell耗能结构的等效阻尼及等效刚度，且有限谱矩相同的个数越多，等效精度越高。由于单自由度一般粘弹性阻尼器结构频响函数的零阶、一阶和二阶谱矩易于用解析法或高斯积分公式法或数值积分法获得，故本文提出的等效准则将为单自由度一般粘弹性耗能结构的等效阻尼和刚度分析提供了可行路径。

② 基于零阶和二阶谱矩相同准则，所获得的单自由度Maxwell阻尼器耗能结构的解析等效阻尼及频率，在我国抗震规范要求的参数范围内，即：ω0λ≤1/3，且附加阻尼比不超过20 %；其计算精度明显优于经典的模态应变能方法所得结果。