基于MATLAB的全地形车辆被动悬架动力学分析

孙 峰 张思崇戴 磊郭凌崧

（1-江苏林海动力机械集团有限公司 江苏 泰州 225300 2-天津大学内燃机研究所）

引言

悬架系统的作用是将车轴与车身连接起来以减轻由于路面不平而传给车身的冲击和振动，以及传递作用在车轮和车身之间的力和力矩。显然，悬架系统对于提高车辆操纵稳定性，确保车辆安全功能起着重要作用[1-2]。

在车辆悬架设计中，悬架应满足以下基本要求：行驶舒适性、减少动态道路轮胎力、减少车体之间的相对运动。悬架系统分为被动、半主动、主动悬架[3-4]。对于车辆动力学，车辆模型分为3类：整车模型，1/2车模型及1/4车辆模型[5]。1/4车辆模型是最简单的2自由度一维模型，它假设车辆前轴和后轴的运动独立振动，广泛应用于车辆悬架的研究和设计[6-8]。本文研究的全地形车辆（Utility Vehicle），前后悬架均为双横臂式独立悬架，结构形式属于被动悬架，下文以前悬架为代表进行动力学研究。

1 悬架系统数学模型的建立

通过三坐标扫描获得全地形车辆悬架系统重要零部件关键点的坐标值，利用逆向工程方法建立该全地形车辆双横臂式独立前悬架系统的三维模型，如图1所示。

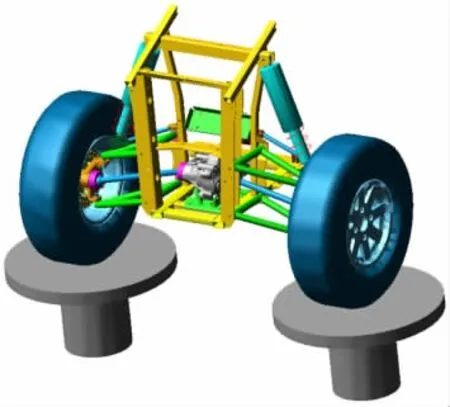
图1 某全地形车辆前悬架系统动态仿真模型

前悬架系统为左右对称结构，因此在建立悬架系统数学模型时，下文以1/4车辆模型（前右悬架）为研究对象。尽管如此，前右悬架仍为一个复杂的多体系统，包括车轮及其附件、轮胎、减震器、悬架元件和1/4底盘及其刚性连接部件[5]。

在建立悬架系统数学模型前，需要对悬架系统进行合理的简化抽象概述。图2为1/4车辆简化模型，其中，m1为簧下质量，m2为簧载质量，k1为轮胎的垂直刚度，k2为悬架的刚度系数，c1为轮胎的阻尼系数，c2为悬架的阻尼系数，x1为簧下质量的垂直位移，x2为簧载质量的垂直位移，y为路面激励。

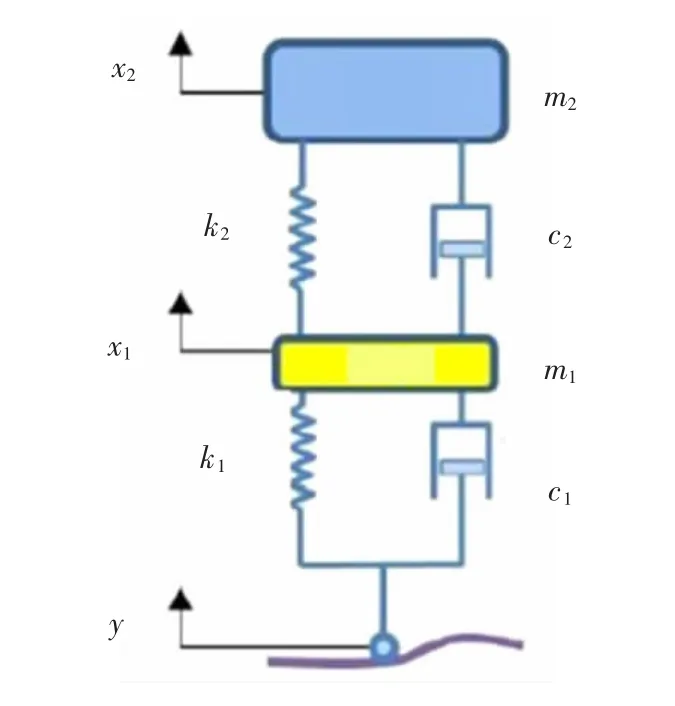
图2 1/4车辆模型简图

对该1/4车辆模型进行受力分析，可以得到该悬架系统运动微分方程：

对上式进行变换得到：

表1给出了某全地形车辆的1/4车辆模型的参数。

表1 某全地形车辆的1/4车辆数学模型参数

参数y表示路面激励，它是不规律的，可以选取多种不同类型，路面常见的驼峰有：弧形驼峰、梯形驼峰和多项式驼峰[9]。车辆以不同车速经过驼峰时的振动响应也会不同。本文选取阶跃函数作为路面激励，幅值为0.1 m，作为输入函数来分析该悬架系统的动态特性，如图3所示。

图3 阶跃激励函数

2 悬架系统数学模型求解

对于方程（3）和（4）所表述的1/4车辆模型二阶微分方程组，直接求解比较困难。MATLAB具有强大的数值方法来求解微分方程，本文使用MATLAB软件对其进行求解[10-13]。

2.1 使用ODE45编程求解

ODE是MATLAB专门用于求解微分方程的功能函数。其中，ODE45求解器是一种自适应步长（变步长）的常微分方程数值解法，它采用了Runge-Kutta算法，是目前解决数值解问题的首选方法，而它只对一阶方程有效[11]。

方程（3）和（4）是二阶微分方程，为了求解该方程组，我们必须把它简化成两个一阶微分方程。这里

通过引入新的变量来表示x˙2和x˙1，从而将方程（3）和（4）转换为适合MATLAB求解的标准形式。令：

则有：

通过引入中间变量达到了降阶的目的。此时有4个未知量v2，v1，x2，x1，可将方程（5）～（8）写成：

式（9）为一阶常微分方程组，即为MATLAB求解的标准形式。

这里通过MATLAB函数编程求解上述运动微分方程组。首先编写一个单独的函数文件来定义方程（9）；然后应用ODE45求解器调用该函数，对运动方程进行求解；最后绘制所需结果曲线图。运行程序，可以得到车辆在阶跃激励作用下的簧载质量位移、簧下质量位移和两者位移之差，如图4所示。其中，x2表示簧载质量位移，x1表示簧下质量位移，x2-x1表示车身相对轮胎位移。

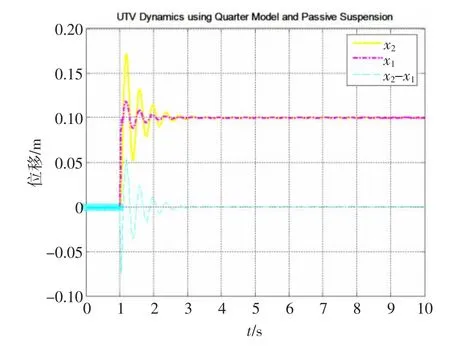
图4 利用ODE45函数求解悬架系统运动微分方程

虽然利用ODE45函数编程可以求解微分方程，但是由于MATLAB函数运行方式比较抽象，因此理解和应用起来也较困难。除了可以直接通过函数编程（ODE45）来求解微分方程，MATLAB还提供了一些基于ODE45求解器开发的专用模块，包括状态空间模型（State-Space block）、传递函数（Transfer-Function block）和Matlab/Simulink[10]。这3种求解方法相比ODE45函数编程，数学模型和参数都易于理解，应用起来比较容易。

2.2 使用状态空间模型求解

系统的微分方程描述是可以转化为状态空间模型的。因此，对于悬架系统运动微分方程组的求解，可以将系统运动微分方程转化为状态空间模型，通过求解状态空间模型来达到求解微分方程的目的。状态空间模型的一般形式为：

其中：X（t）表示状态变量，U（t）表示输入（或控制）变量，Y（t）表示输出变量，A（t）表示状态（或系统）矩阵，B（t）表示输入矩阵，C（t）表示输出矩阵，D（t）表示直接转换矩阵。

将方程（3）和（4）写成矩阵形式：

设定悬架系统的状态变量为：

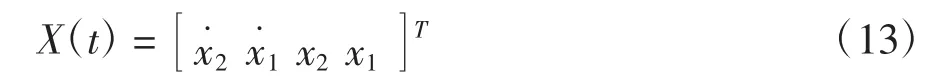
则有：

方程（14）和（15）即为该悬架系统运动方程的状态空间模型。对于方程（14）和（15），在Matlab/Simulink中使用State-Space Block进行求解，如图5所示。图5a为悬架系统的状态空间模型，图5b为悬架系统的状态空间模型参数。

图5 悬架系统的状态空间模型

将表1中所列的该车辆悬架模型参数以及图3所示阶跃函数输入到图5对应参数中。运行该程序，得到悬架系统的输出变量：簧载质量位移x2、簧下质量位移x1、车身相对轮胎位移x2-x1，如图6所示。

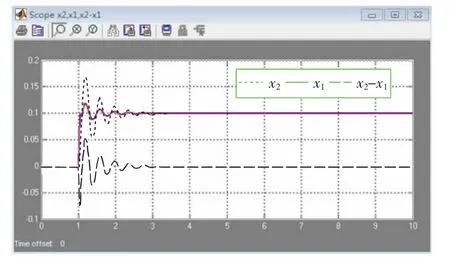
图6 车辆悬架系统模型的输出变量

2.3 使用传递函数求解

对于系统微分方程的求解，除了可以将其转化为状态空间模型进行求解，还可以使用传递函数来表述。对方程（1）和（2）进行拉氏变换，车辆悬架系统运动微分方程可写为：

由方程（16）可得：

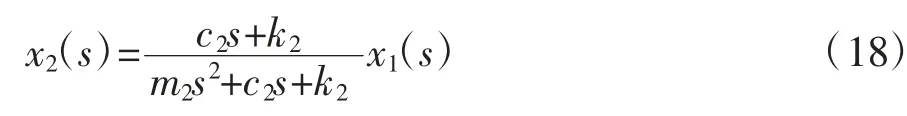
将方程（16）和（17）相加得到：

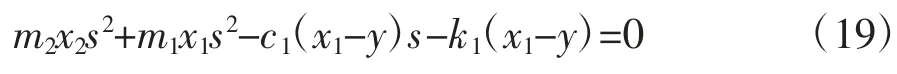
将方程（18）带入方程（19）得到：

对上式化简即可得到轮胎位移x1相对路面激励y的传递函数：

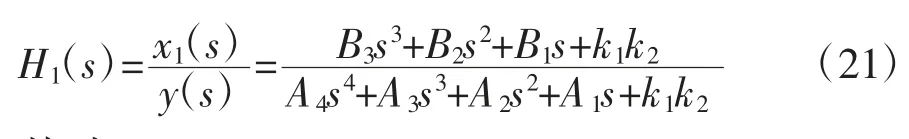
其 中：A4=m1m2，A3=m2c2+m2c1+m1c2，A2=m2k2+m2k1+m1k2+c1c2，A1=c2k1+c1k2，B3=m2c1，B2=m2k1+c1c2，B1=A1=c2k1+c1k2。

对于方程（21），可在Matlab/Simulink中使用Transfer Function Block进行表述，如图7所示。

图7 簧下质量位移相对路面激励的传递函数模型

将表1中所列悬架系统参数和图3所示阶跃函数输入到图7参数中。运行该程序，得到轮胎在阶跃激励下的垂直方向位移变化曲线，如图8所示。

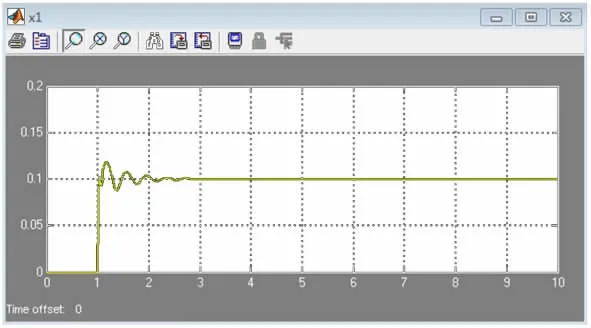
图8 簧下质量位移阶跃激励响应曲线

类似地，可以得到簧载质量位移x2相对路面激励y的传递函数：

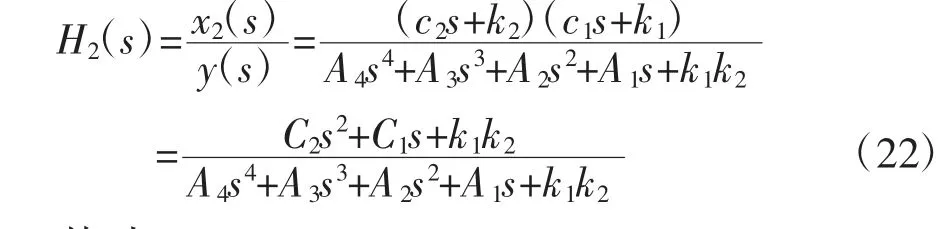
其 中：A4=m1m2，A3=m2c2+m2c1+m1c2，A2=m2k2+m2k1+m1k2+c1c2，A1=c2k1+c1k2，C2=c1c2，C1=A1=c2k1+c1k2。

对于方程（22），在Matlab/Simulink中使用Transfer Function Block进行表述，具体步骤与图7表述类似，这里不再赘述。运行程序，得到车身在阶跃激励下的垂直方向位移变化曲线，如图9所示。

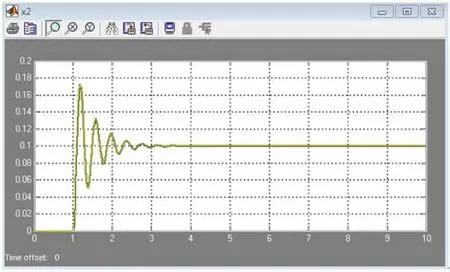
图9 簧载质量位移阶跃激励响应曲线

同理，可以得到车身相对轮胎位移变化量对于路面激励的传递函数：

其 中：A4=m1m2，A3=m2c2+m2c1+m1c2，A2=m2k2+m2k1+m1k2+c1c2，A1=c2k1+c1k2，D3=-m2c1，D2=-m2k1，D1=0，D0=0。

对于方程（23），可在Matlab/Simulink中使用传递函数进行表述，相关步骤与上面类似，此处不再赘述。运行程序，得到在阶跃激励下车身相对轮胎垂直方向位移变化曲线，如图10所示。

图10 簧载质量相对簧下质量位移阶跃激励响应曲线

车身位移变化量仅仅表示振动幅值大小，而车辆乘坐舒适性通常以车辆通过驼峰时的最大簧载质量加速度来衡量。簧载质量加速度是簧载质量位移相对时间的二阶导数。其中，位移、速度、加速度三者之间的关系为：

方程（1）和（2）按照加速度、速度、位移变量来表达，可以写为：

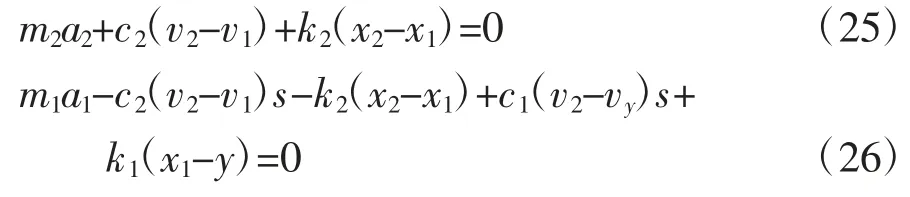
对方程（24）～（26）进行拉氏变换，得到：

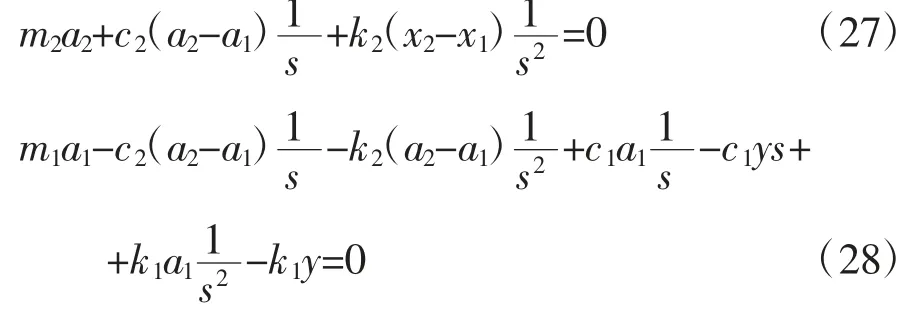
与方程（18）～（21）类似处理，可以得到簧载质量加速度a2相对路面激励y的传递函数：

其 中：A4=m1m2，A3=m2c2+m2c1+m1c2，A2=m2k2+m2k1+m1k2+c1c2，A1=c2k1+c1k2，E4=C2=c1c2，E3=C1=c2k1+c1k2，E2=k1k2，E1=0，E0=0。

对于方程（29），在Matlab/Simulink中使用传递函数进行表达求解，具体步骤与图7表述类似。运行程序，得到在阶跃激励下的车身垂直方向加速度变化曲线，如图11所示。

图11 簧载质量加速度阶跃激励响应曲线

2.4 使用Matlab/Simulink模块求解

使用状态空间模型和传递函数方法求解微分方程，都需要将系统运动微分方程转化为相应的模式再进行求解。而Matlab/Simulink模块，可以对系统运动微分方程组（方程（3）和（4））直接输入表达进行求解，如图12所示。

图12 利用Matlab/Simulink求解悬架系统运动微分方程

将表1中所列参数数值和图3所示路面激励函数输入到图12中的Matlab/Simulink模块对应参数。运行该程序，可以得到悬架系统运动方程的状态变量在路面激励状况下的响应曲线，如图13所示。

可以看出，簧下质量位移波动较小，簧载质量位移波动振幅较大（振动最大幅值约为激励幅值的1.7倍），说明轮胎受路面激励变形很小，而车身受路面激励影响产生较大振动；图13c和图13d能较近似反映车辆乘客的乘坐舒适性，在激励产生后的前2 s，乘客会受到较大振动幅值的影响。

图13 1/4车辆模型在路面阶跃激励下的响应

由以上分析可以发现，使用状态空间模型、传递函数和Matlab/Simulink模块3种方法求解得到1/4车辆模型运动微分方程输出变量，与使用ODE45函数求解得到的结果是一致的。但从操作难易、实际应用等方面考虑，求解微分方程时可优先使用Matlab/Simulink模块，再者是状态空间模型和传递函数，最后是ODE45求解器。

根据ISO 2631[13]要求，乘坐的舒适度范围是车身垂直加速度不超过0.8 m/s2。由图11和图13d可以发现，阶跃激励作用的前2 s，车身加速度几乎都超过该限值。因此，该车辆的乘坐舒适性还有进一步提升的空间。

3 悬架阻尼对车辆振动的影响

本文研究的某全地形车辆悬架系统为被动悬架，悬架阻尼为固定值750 Ns/m。为了分析悬架阻尼对车辆动力学的影响，设定悬架阻尼c2的取值分别为250 Ns/m、500 Ns/m、750 Ns/m、1 000 Ns/m及1 250 Ns/m，再次通过ODE45函数编程，得到在相同的路面阶跃激励作用下，车辆悬架阻尼取不同值时对应的5组悬架系统簧载质量位移变化曲线，如图14所示。

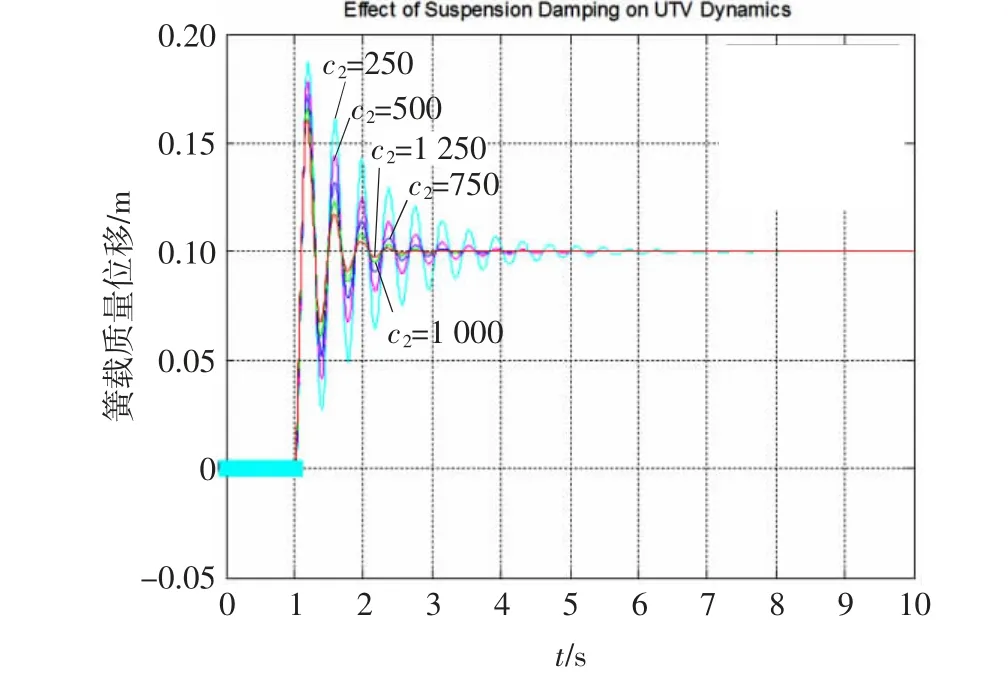
图14 悬架系统选取不同阻尼时的输出变量

可以发现，悬架阻尼对车辆振动的影响还是比较大的。悬架阻尼较小时，虽然单位时间内振幅不大，但振动衰减比较缓慢，乘坐舒适性相对较差；悬架阻尼较大时，虽然振动衰减时间短，但单位时间内振幅较大，乘坐舒适性也不太好。本文研究的某全地形车辆悬架阻尼值介于中间，比较合理。

4 结论

1）通过逆向工程技术建立了某全地形车辆前悬架系统三维模型，并将其简化为1/4车辆数学模型。

2）分别使用状态空间模型方法和传递函数及Matlab/Simulink模块3种方法对所建的数学模型运动微分方程进行了求解，与使用ODE45求解器得到结果具有一致性，并给出优先使用顺序。

3）以簧载质量位移和加速度作为乘坐舒适性评价指标对某全地形车辆的振动特性进行了分析，为进一步研究车辆动态特性奠定了基础。

4）分析了悬架阻尼对车辆振动的影响，验证了某全地形车辆悬架阻尼设计的合理性，对提升车辆乘坐舒适性具有一定理论指导意义。