Efficient Construction of B-Spline Curves with Minimal Internal Energy

Gang Xu ,Yufan ZhuLishan DengGuozhao Wang,Bojian Li and Kin-chuen Hui

Abstract:In this paper,we propose an efficient method to construct energy-minimizing B-spline curves by using discrete mask method.The linear relations between control points are firstly derived for different energy-minimization problems,then the construction of B-spline curve with minimal internal energy can be addressed by solving a sparse linear system.The existence and uniqueness of the solution for the linear system are also proved.Experimental results show the efficiency of the proposed approach,and its application in G 1blending curve construction is also presented.

Keywords:Minimal energy,B-spline curves,geometric construction,discrete mask method,sparse linear system.

1 Introduction

Curve and surface modeling is a basic problem in the field of Computer Aided Geometric Design.Energy-minimization curve and surface has nice geometric properties,which makes it been widely used in fairing curve/surface design,computer vision and image processing [Li,Wang and Zhu (2013)].Hofer [Hofer (2004)] proposed the application of energy-minimizing curves in Manifolds.

There is a huge body of literature on the energy-minimizing curves in CAGD [Higashi,Kaneko and Hosaka (1988); Meier and Nowacki (1987); Qu and Ye (2000); Rando(1990); Zhang,Zhang and Cheng (2001)].Higashi et al.[Higashi,Kaneko,and Hosaka(1988)] proposed construction of cubic Bé zier curves with smoothly varying curvature specified by position,tangent and curvature.Rando proposed the calculation of Bé zier curve minimizing the variation of the radius of curvature [Rando (1990)].Hagen and Bonneau proposed a variational approach for designing the weights of a rational curve to achieve a smooth curve with minimal energy integral [Hans and Georges-Pierre (1991)].Jou and Han investigated the minimal energy splines with various constraints [Han and Jou (1992)].Moreton and Sequin presented a nonlinear algorithm for curves and networks with minimal variation of curvature [Moreton and Sequin (1992)].The algorithm for fairing cubic spline curves by minimizing the strain energy was proposed by Zhang et al.[Zhang,Zhang and Cheng (2001)].Brunnett proposed two variational models of fair curves for motion planning [Brunnett,Hagen and Santarelli (1993)].The geometric Hermite curves with minimal strain energy were investigated by Yong et al.[Yong and Cheng (2004)].Johannes Wallner proposed the existence of set-interpolating and energy-minimizing curves [Wallner (2004)].A constructive framework for energyminimizing curve with a set of interpolating points were proposed in Johnson et al.[Johnson and Johnson (2016)].Wesselink et al.[Wesselink and Veltkamp (1995)]proposed the construction of constrained variational curves using external energy operators.Most of the previous work uses iteration numerical method to generate energyminimizing curves or curve networks.Xu et al.studied the geometric construction method of Bé zier curve with minimal energy [Xu,Wang and Chen (2011)].Given some control points,the unknown control points can be obtained by geometric operation such that the resulted Bé zier curve has minimal energy.

In this paper,we propose an efficient mask approach to construct the energy-minimizing B-spline curve by solving a sparse linear system.Firstly,we derive some linear conditions for control points of energy-minimal curves,then the linear constraint is written in a mask way,which can be extended to the construction of energy-minimizing B-spline curves.In contrast to solving a dense linear system in traditional methods,the unknown control points of energy-minimizing B-spline curves can be constructed by solving a sparse linear system.Several modeling examples are presented to illustrate the effectiveness of the proposed approach,and its application inG1blending curve construction is also investigated.

2 Efficient construction of energy-minimizing B-spline curves

Stretch energy and strain energy are two kinds of well-known internal energy of parametric curves,which typically depend on intrinsic geometric information of the planar curve such as the length and curvature.

The internal energy of a Bé zier curve can be written in a unified way:

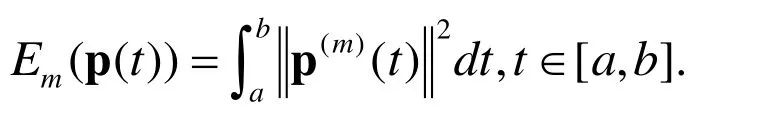
Whenm=1,it is called stretch energy related to the length of a curve.Whenm=2,it is called strain energy,which measures how much the curve is bent.

2.1 Discrete mask for energy-minimizing curve construction

Theorem 2.1.The control points in=｛Pi｝i∈Dminimize the energy functionEm(p(t))with given control points in=｛Pi｝i∈Gif and only if they satisfy

where

From above theorem,the unknown control points can be obtained via solving the dense linear system (1) of equations.However,the computing cost of each entry in the coefficient matrix is high,on the other hand,currently the existence and uniqueness of the solution for the linear system (1) is unclear.Thus,it is not an efficient way to construct energy-minimizing B-spline curves.In this paper,we propose a discrete mask method to construct B-spline curves with minimal energy efficiently.

Firstly,we will derive some discrete masks from the energy-minimizing constraint condition of Bé zier control points.Whenm=1andn=4,supposed that P0,P1,P3and P4are given control points,the control point P2should satisfy the following condition according to Theorem 2.1:

Similarly,whenm=2andn=4,the control point P2should satisfy the following condition according to Theorem 2.1:

Suppose that the four ending control points P0,P1,Pn-1and Pnof B-spline curve are given.By extending the relationships shown in (2) and (3) to the general form,the unknown control points of B-spline curves should satisfy the following requirements in order to achieve energy minimization:

where Piare the unknown control points,i∈[2,n-2].For stretch-energy-minimization problem,we setfor strain-energy-minimization problem,we set

Those linear relationships among undetermined control points comprise make up a linear system:

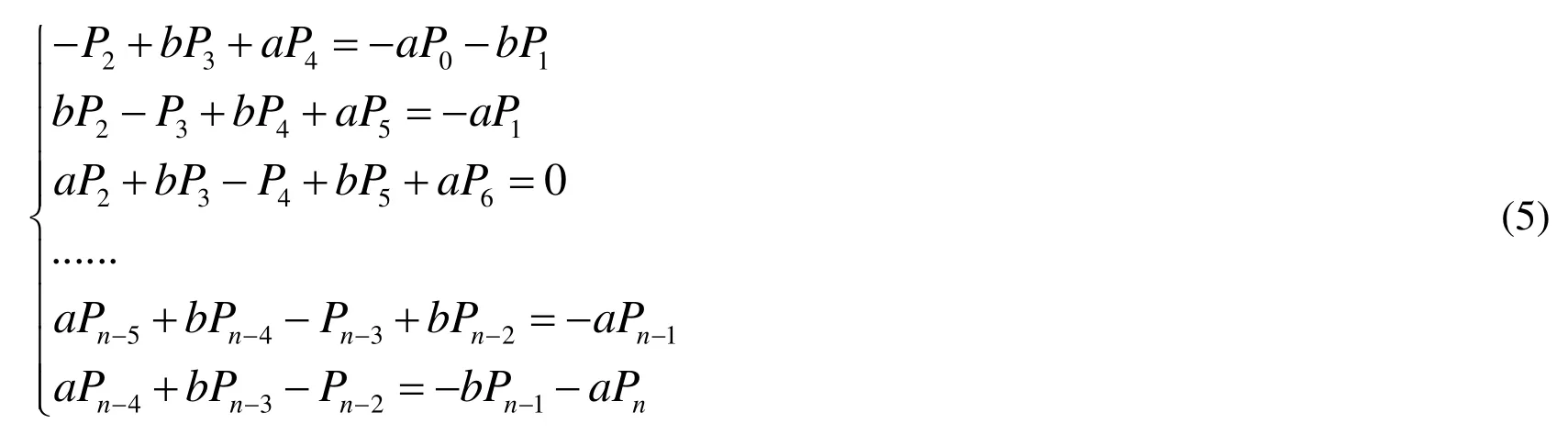
That is,

in which the coefficient matrix Mnhas the follow form:

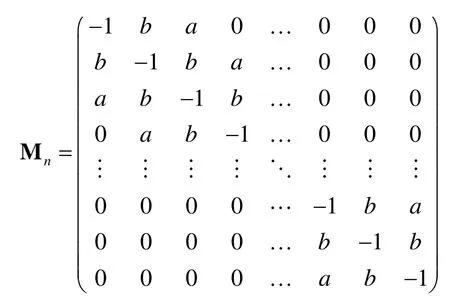
From the proposed mask method,given partial control points of B-spline curves,the unknown control points can be obtained by solving the corresponding sparse linear systems (6) to satisfy the minimization requirements for stretch energy and strain energy.

2.2 Existence and uniqueness of the solution

In this subsection,we will prove the existence and uniqueness of the solution for the sparse linear system (6) with respect to the masks for stretch and strain energy minimization.LetHn= d et(M).IfHn≠0,then there exists a unique solution for the linear system (6).Firstly,we give the computation method for the determinant of Mnin the following proposition.

Proposition 2.1.LetHn= d et(Mn),thenHnCan be computed in a recursive way:

Proof.Firstly,we construct the following two kinds of determinants:

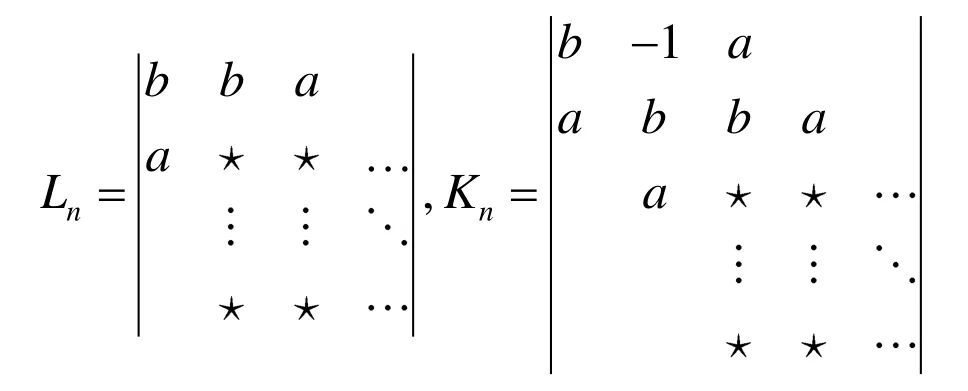
in which denotes the matrix with the same structure as Mn.

Then we have

After some simple computation from (8)(9)(10),we can get the recursive formula (7).

Thus,the proof is completed.

In order to computeHn(n＞5)recursively,H0,H1,H2,H3,H4andH5should be firstly obtained as follows,

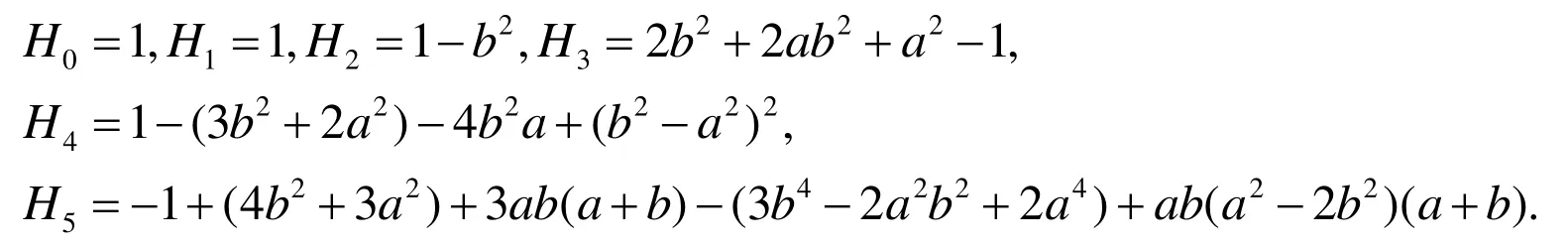
According to Eq.(2),the mask of stretch energy minimization is defined as:

The corresponding coefficient matrix M1nis:

According to Eq.(3),the mask of strain energy minimization is given as:

The corresponding coefficient matrix M2nis:

In the following,we will prove that there exists a unique solution for the sparse linear systems of stretch energy and strain energy minimization.

Proposition 2.2.i.e.,there exists a unique solution for the sparse linear systems of stretch energy and strain energy minimization.

Proof.From (7),we can get the characteristic polynomial of Mnas follows,

λ6+λ5-(a2-b2)λ4-a2(a2-b2)λ3-2a(b2+a)λ2+a4λ+a6=0.

By solving (11),we can obtain the three rootss1,s2ands3.Then we can get the six rootsλ1,λ2,λ3,λ4,λ5andλ6for the characteristic polynomial of Mn.By direct computation,we can find that all the eigenvaluesλ1,λ2,λ3,λ4,λ5,λ6are non-zero,in case ofThat is,Hn≠0,the coefficient matrix M1nand M2nfor stretch energy and strain energy minimization is invertible.Thus,the proof is completed.

3 Experimental results

3.1 Modeling examples of energy-minimizing curves

In this section,some experimental examples will be presented to show the effectiveness of the proposed method for construction of energy-minimizing curves.These two modeling examples are selected according to the different distribution type of the input control points.

Example I.In this example,the given control points are P0=(-1 .2,-0.4),P1=(-0.8,0.1),Pn-1= (0.6,-0.5)and Pn=(1.0,0.5).Fig.1 and Fig.2 show B-spline curves with minimal stretch and strain energy constructed by the proposed approach with the same specified control points but different number of unknown control points.We can find that in Fig.1 some B-spline curves with minimal length can be achieved,and in Fig.1 we can obtain some B-spline curves with minimal curvature under the input constraints.

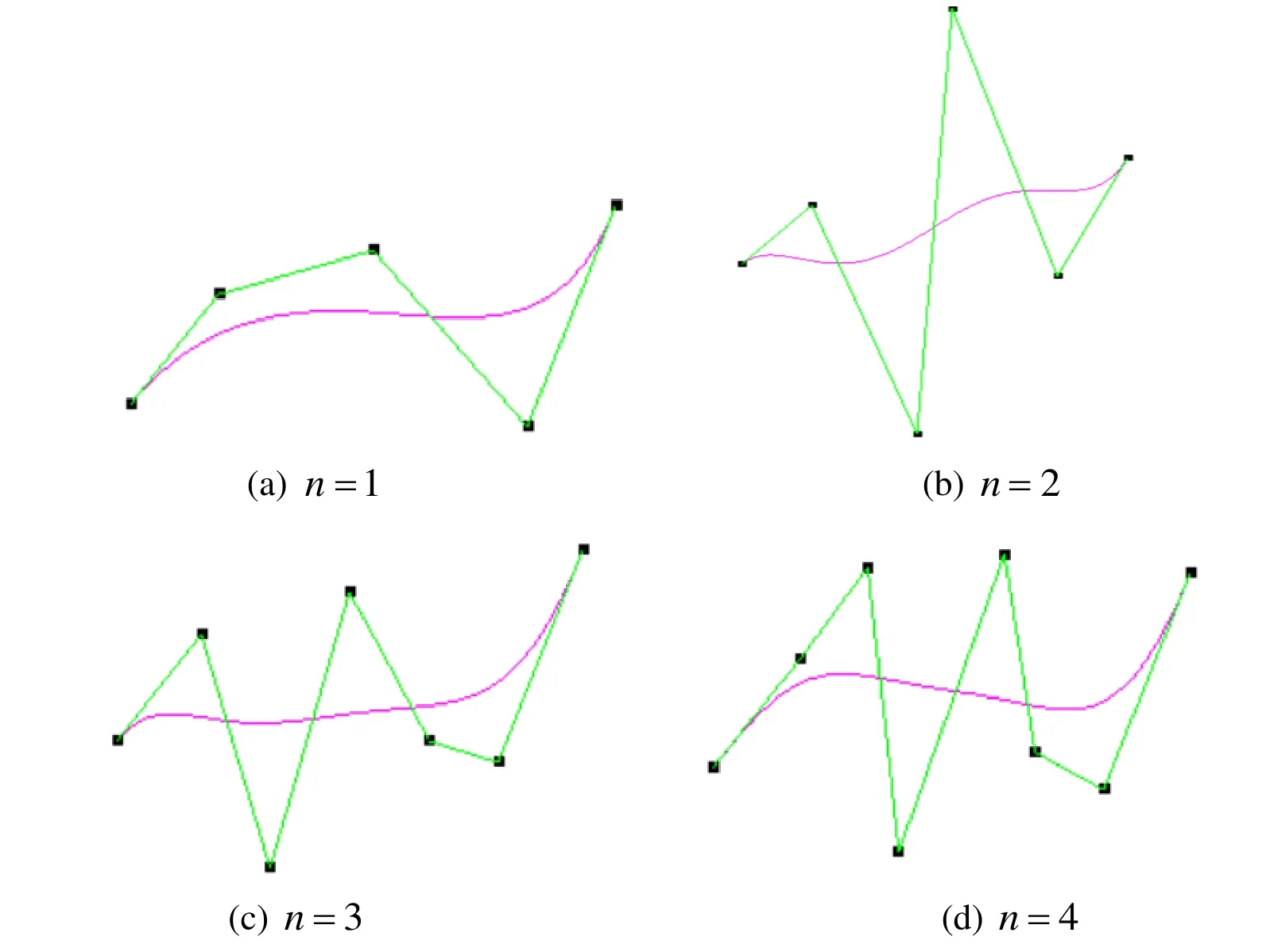
Figure1:B-spline curve with minimal stretch energy in Example I.

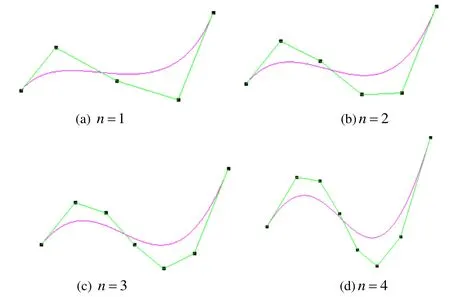
Figure2:B-spline curve with minimal strain energy in Example I

Example II.In this example,P0=(-1 .2,-0.4),P1=(-0.8,0.4),Pn-1= (0.6,-0.1)and Pn= (1.0,-0.2)are the specified control points.The corresponding energyminimizing B-spline curves are shown in Fig.3 and Fig.4 respectively.Similarly,we can find that B-spline curves with minimal length can be achieved in Fig.3,and B-spline curves with minimal curvature can be obtained in Fig.4.

In order to show the computing efficiency of the proposed method,some testing results for examples with large number of unknown control points are presented in Tab.1,Fig.5 and Fig.6,including the comparisons with traditional methods.The time shown in this table includes the time for the computing of coefficients matrix entry and the time for solving linear systems.It can be found that a significant efficiency improvement can be achieved with the proposed discrete mask approach.

Figure3:B-spline curve with minimal stretch energy in Example II

Figure4:B-spline curve with minimal strain energy in Example II,in which n is the number of unknown control points

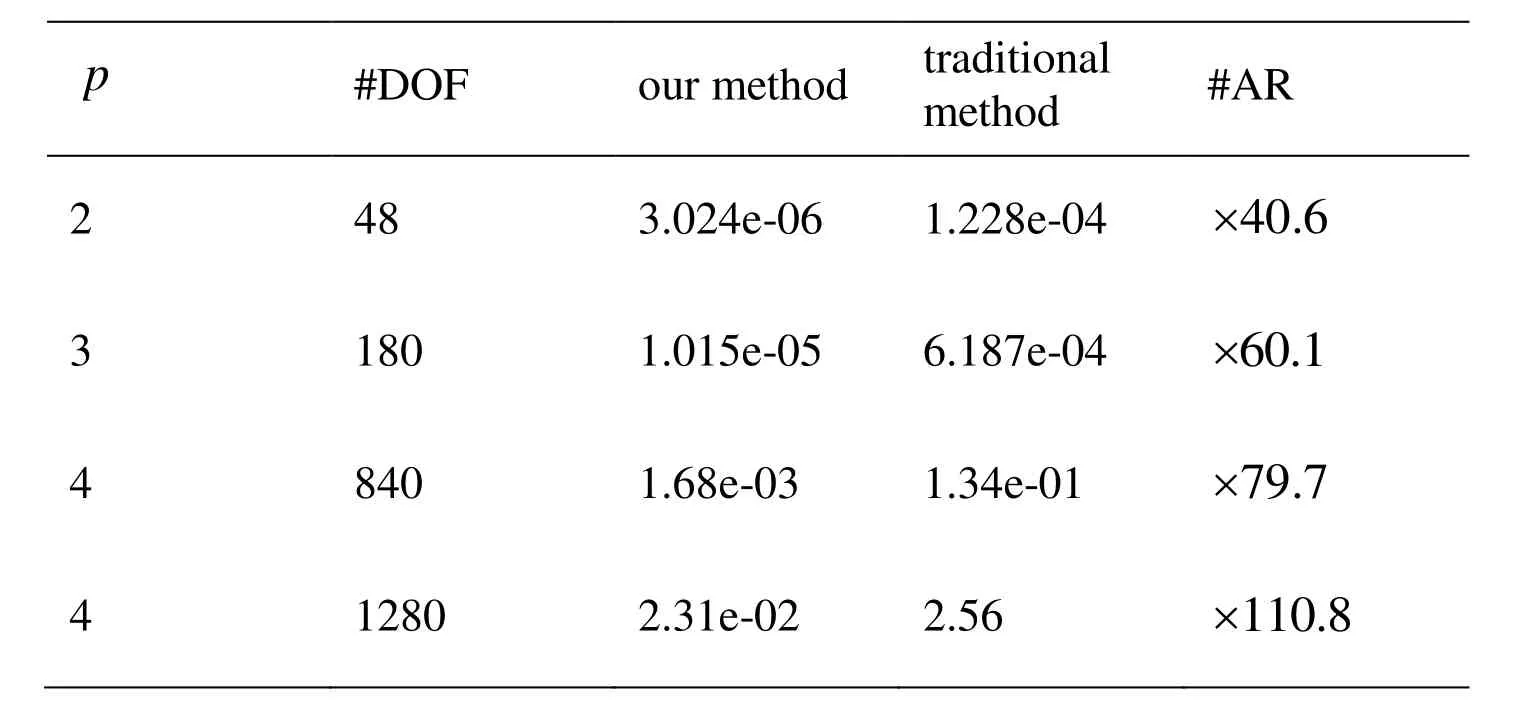
Table1:Quantitative data and timing costs (in seconds) for energy-minimizing curve construction (#DOF:the degree of freedom; p:the degree of B-spline curves; #AR:acceleration ratio)

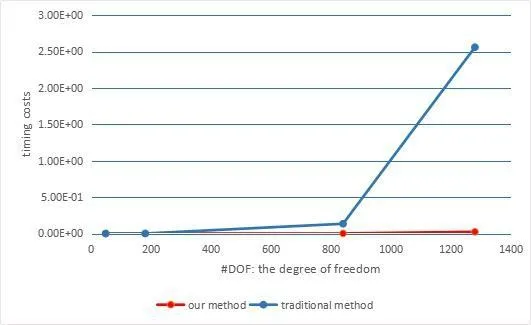
Figure5:Timing costs for energy-minimizing curve construction in Tab.1

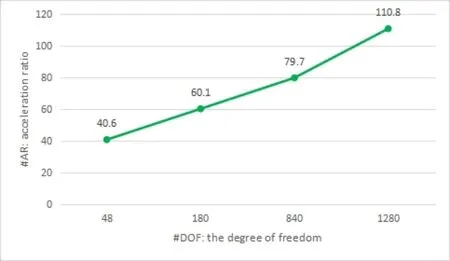
Figure6:Acceleration ratio comparison for different degrees of freedom as shown in Tab.1

3.2 Application in blending curve construction

Construction of blending curves between two given curves is one of the fundamental problems in CAGD [Lin,Xiong and Liao (2014)].The blending problem can be stated as follows:two separate B-spline curves are given,how to construct a smooth curve to connect these two given curves while satisfying certain continuity conditions between them.The proposed energy-minimizing curve construction method can be used to address this problem.Firstly,we need to construct the two starting and ending control points of the blending curve to be constructed with-continuity according to the control polygon of given two B-spline curves; then the remaining control points of the blending curve are constructed by the proposed approach to satisfy the energy-minimization constraints.This method is intuitive,simple and easy to implement.Three modeling examples of blending curve construction are given in Fig.7,Fig.8 and Fig.9,in which the pink curves are the specified curve,the blue curves are the blending curves with minimal strain energy,and the red ones are the blending curves with minimal stretch energy,the green lines are the control polygons of the B-spline curves.

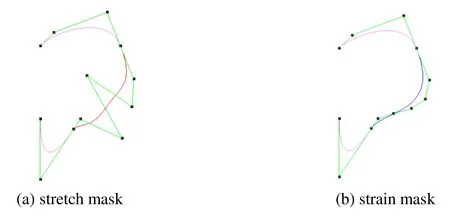
Figure7:Blending curve construction for ear contour

Figure8:Blending curve construction for font modeling

Figure9:Blending curve construction for dolphin contour

4 Conclusion

In this paper,we propose a discrete mask method to construct energy-minimizing B-spline curves efficiently by solving a sparse linear system.A proof is given for the existence and uniqueness of the linear system solution.The efficiency of the proposed method is illustrated by some experimental results,in which the application inG1blending curve construction is also presented.

As a part of future work,the proposed approach can be extended to other mask types,such as the mask with three specified ending control points,which can be used to construct blending curves withG2-continuity.Furthermore,we are going to apply the proposed method in path-planning for robotics applications.

Acknowledgement:Thanks for the reviewers’ comments to improve the paper.This research was supported by the National Nature Science Foundation of China under Grant Nos.61772163,61761136010,61472111,Zhejiang Provincial Natural Science Foundation of China under Grant Nos.LR16F020003,LQ16F020005.