双稳健半参模型法评价CAF和TAC化疗方案治疗乳腺癌疗效的回顾性分析*

潍坊医学院(261053)

田 野 马 洁 黄 璐 杜泽玉 吕军城 石福艳 孟维静 王素珍△ 潘庆忠△

队列研究是临床流行病学重要的研究方法之一,在研究反应变量与处理因素之间关系的因果推断中,随机对照试验(randomized controlled trials,RCT)被视为评价临床试验干预措施的金标准。但在实际的临床实践中,由于受样本量、研究费用、持续时间以及伦理学等方面的因素影响,随机对照试验的实施受到很大的制约[1]。近年来,非随机对照研究、队列研究、临床数据挖掘等临床流行病学方法在循证医学领域广受关注。观察性临床研究不同于RCT临床试验可以按照试验设计进行随机分组从而减少混杂因素所产生的偏倚。如果在回顾性队列研究资料进行分组后直接比较处理效应，所做出的统计结论容易增大犯II类错误的概率,当协变量数目较多且无法精确获知其对处理分配和生存结局的影响时,直接估计未调Kaplan-Meier值及生存曲线会导致偏倚,因此,对于传统的倾向性评分(propensity score,PS)方法如匹配法、分层法、加权法等应用于生存资料分析时并不容易实现[2]。

基于PS双稳健半参模型法是对传统PS方法的改进,自20世纪90年代Scharfstein[3]首次引入双重稳健模型的概念以来,近些年其得到了众多的关注和研究[4]。有研究结果显示,在生存资料分析时应用双稳健模型可以直接估计出处理(暴露)对生存结局的绝对和相对效应[5],最大程度地减小混杂偏倚。本文以乳腺癌患者常用的CAF(环磷酰胺、多柔比星、氟尿嘧啶)和TAC(多西他赛、多柔比星、环磷酰胺)两种化疗方案为例,运用基于PS的 IPTW和DRIPTW、SMRW和DRSMRW(IPTW:inverse probability of treatmentweighting;SMRW:Standardized mortality ratio weighting;DRIPTW:Doubly robustinverse probability of treatmentweighting;DRSMRW:Doubly robust Standardized mortality ratio weighting)等多种PS改进模型分析不同化疗方案对乳腺癌患者的因果效应和预后结果的影响,从而使研究结果更接近“真实世界(realword,RW)”的实际干预效果,最终为临床实践提供可靠的循证依据。

对象与方法

1.研究对象

从美国SEER(surveillance,epidemiology,and end results)肿瘤患者纵向数据库中,选择2000年到2012年12年间的乳腺癌患者作为研究对象,排除无法使用的病例,共计800例,其中CAF组513例,TCA组287例。收集的指标有:手术类型(1:CAF方案,2:TAC方案)、年龄(岁)、婚姻状况(1:单身,2:已婚,3:离婚,4:丧偶,5:未知)、偏侧化(1:乳房左侧,2:乳房右侧,3:双侧)、肿瘤性质(1:原位癌,2:恶性转移癌)、分期(1:Ⅰ期,2:Ⅱ期,3:Ⅲ期,4:Ⅳ期)、肿瘤大小(mm)、癌胚抗原CEA(1:有,2:无)、糖类抗原CA15-3(1:有,2:无)、生存状态(0:生存,1:死亡)、生存时间(月)等。

2.基于PS的双稳健半参模型法的基本原理

Rosenbaum和Rubin[6]把PS定义为:在可观察的协变量(Xi)条件下,研究对象i(i= 1,2,…,N)接受某种处理(或暴露)因素(Zi=1)而非对照因素(Zi=0)的条件概率,计算公式为:

e(X)=Pr(Z=1|X=Xi)

如果协变量Xi为分组变量Zi相互独立,那么对任意Xi,有:

e(X)或者P,即倾向性评分PS。

由公式可得,PS实际上是一个综合多个协变量的函数,其值在0和1之间[7]。倾向评分PS方法可以平衡协变量的影响,在组间协变量均衡的前提下,对平均因果效应(average causal effect,ACE)做出推断。实际上,倾向评分是用一个函数表示多个协变量共同作用的结果，可以“降维”。经过倾向评分调整后,协变量均衡可比,只有干预因素和治疗效果不同,出现“事后随机化”的效果。

倾向性评分加权法先将主要混杂变量的信息综合成一个变量倾向评分,然后运用标准化法的原理将所得的倾向评分进行加权,通过各对比组中倾向评分分布一致来达到使各混杂因素在各比较组中分布一致的目的[8]。该方法将每一观察单位看作一层,不同倾向评分值预示这一观察单位在两组中的概率不同。在假定不存在未识别混杂因素的条件下,加权调整是基于在一定条件下的两种相反事件的对比来对数据进行调整的,即假设使每个观察对象均接受处理因素和使每个观察对象均不接受处理因素两种相反情况。利用倾向评分估计的权重对各观察单位加权产生一个虚拟的标准人群,在虚拟人群中,两组的混杂因素趋于一致,均近似于某一预先选定的标准人口分布[8]。

倾向性评分加权法的关键在于对权重的计算。IPTW是以所有受试者(试验组和对照组合并的人群)为“标准人群”进行调整。Robins[9]等给出的加权方法得到的人群往往与原人群数量不同,因此虚拟人群各变量的方差大小发生变化。为了得到与原人群的样本量相同的标准人群,Hernan[10]等对计算方法进行了调整,将整个研究人群的处理率和非处理率加入公式进行调整得到稳定权重。具体方法是:试验组观察单位的权重Wt=Pt/PS,对照组观察单位的权重Wc=(1-Pt)/(1-PS)。Pt为整个人群中接受处理因素的比例。SMRW法是将处理组观察对象作为“标准人群”进行调整。Sato和Matsuyama[11]给出的加权系数计算方法是:试验组观察单位的权重Wt=1,对照组观察单位的权重Wc=PS/(1-PS)。同样,由于对照组得到的人群数与处理组样本量一致,而与原对照组样本量不同,因此需要进一步作如下调整,计算其稳定权重:Wc=[PS(1-Pt)]/[(1-PS)Pt]。

双稳健半参模型法是对传统PS法的改进,将PS加权法(边际结构模型)和半参Cox回归模型相结合。具体实施步骤:第一步:估计倾向性评分,包括模型和变量的选择;第二步:计算权重,包括逆概率处理和标化死亡比权重;第三步:均衡性诊断;第四步:生存结局的处理效应估计,包括相对处理效应和绝对处理效应。其中,相对处理效应是将权重进行加权,后估计经加权调整样本的调整 Kaplan-Meier 估计值(adjusted Kaplan-Meier estimator,AKME)及其方差和加权 log-rank 检验;绝对处理效应是双稳健半参模型法的构建,将Zi和对结局有影响的基线协变量与权重共同纳入半参Cox回归模型进行分析,估计HR及其置信区间,起到双稳健的作用。

3.统计方法

定性或等级资料采用构成比描述,定量资料采用均数±标准差表示,两组定性或等级资料比较采用χ2检验,两组定量资料比较采用t检验。PS法分别采用匹配法、加权法和回归调整法,匹配法采用卡钳匹配,卡钳值设为0.02;加权法采用逆概率处理加权法(IPTW)和标准化死亡比加权法(SMRW),并对加权之后的样本进行调整 Kaplan-Meier估计值及其方差和加权log-rank 检验,同时,将各个模型分别与Cox回归模型相结合进行比较。双稳健半参模型法的所有统计分析均采用SAS 9.4编程完成,以P<0.05为差异有统计学意义,检验水准均为α=0.05。

结 果

1．不同方法处理基线资料组间均衡性比较情况

原始资料入选的协变量有:年龄(岁)、婚姻状况、偏侧化、肿瘤性质、肿瘤分期、肿瘤大小(mm)、癌胚抗原CEA、糖类抗原CA153等。在TAC方案组和CAF方案组的基线资料中，两组乳腺癌患者的年龄、婚姻状况、肿瘤性质在匹配前不均衡(P<0.05),而两组患者的肿瘤大小、肿瘤偏侧化情况、肿瘤分期、癌胚抗原CEA含量、糖类抗原CA153含量分布均衡(P>0.05)。在匹配和加权之后,对两组乳腺癌患者协变量进行检验可知,匹配前不均衡的协变量,如年龄、婚姻状况、肿瘤性质等变量经匹配和加权之后在两组的分配达到了平衡(P>0.05),结果见表1～2。

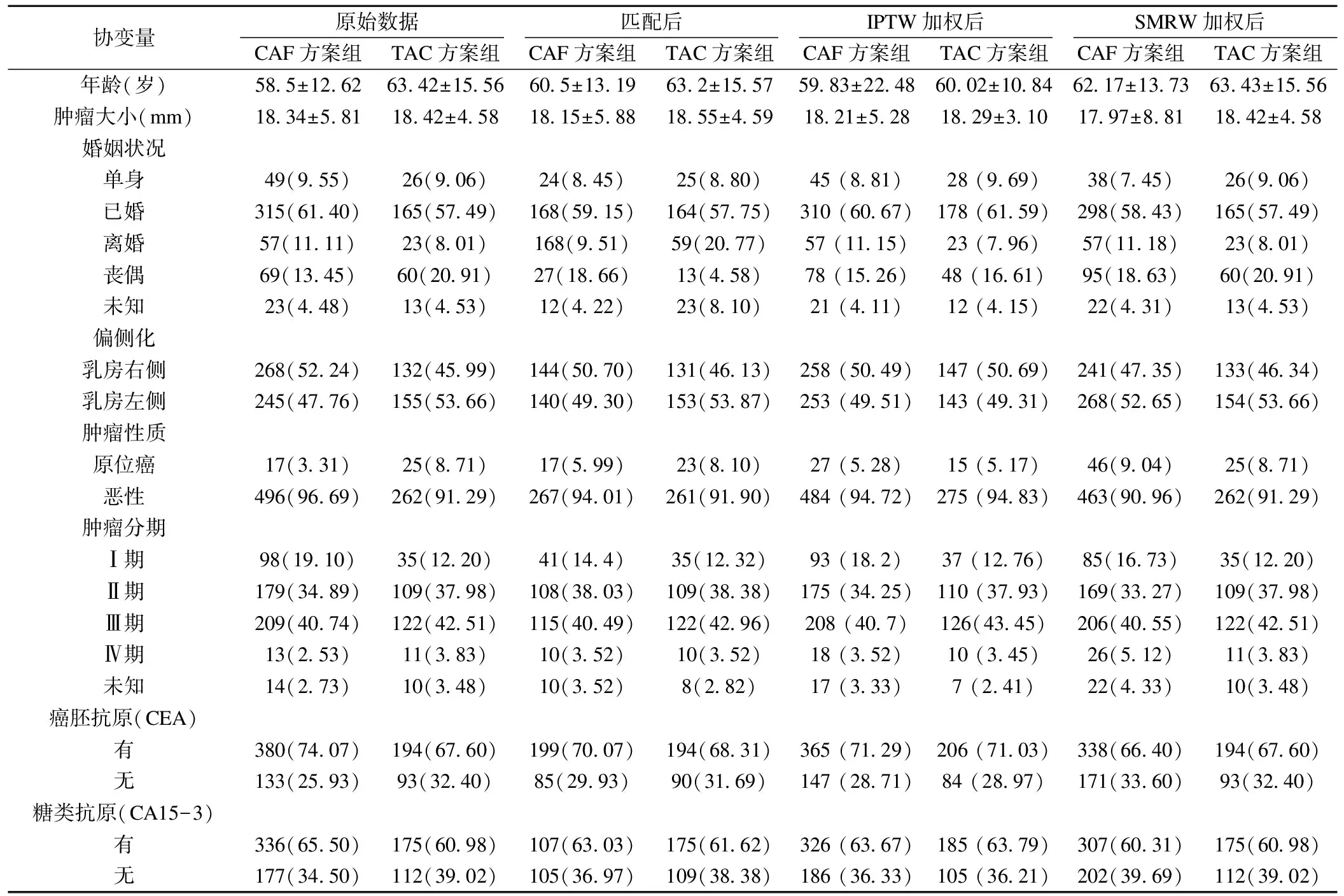
表1 不同方法处理不同样本基线资料之间均衡性情况[n(%)]

表2 不同方法处理基线资料组间均衡性比较情况统计量,P值

2．不同PS方法对TAC方案组和CAF方案组的生存结局的处理效应估计

(1)绝对处理效应估计匹配、稳定逆概率处理加权、稳定标化死亡比加权后的样本TAC与CAF组的生存曲线差异均有统计学意义,见图1(log-rank检验:χ2=25.60,P<0.001;稳定逆概率处理加权log-rank检验:z=2.326,P=0.043;稳定标化死亡比加权log-rank检验:z=1.154,P=0.014)。从生存曲线中可以看出,匹配之后的生存曲线相较于加权调整之后的曲线,其CAF组生存率下降的更快,TAC组与CAF组生存率曲线间存在较大差异。与之相比,加权调整之后的PS-TPTW和PS-SMRT模型中TAC组与CAF组的生存曲线更加稳健。

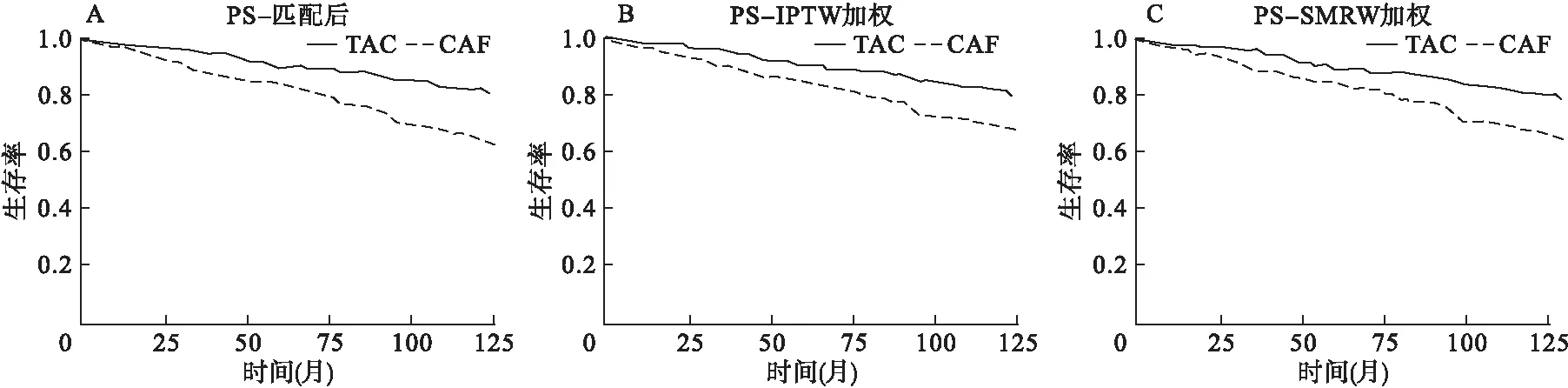
图1 匹配、稳定逆概率处理加权稳定标化死亡比加权后的样本中TAC与CAF组的生存曲线

(2)相对处理效应估计在乳腺癌患者中,以生存结局为因变量,Zi为自变量，进行Cox回归分析估计θ为0.627。以生存结局为因变量,以Zi和对结局有影响的基线协变量为自变量，进行调整Cox回归分析,估计的HR及其置信区间为1.797(1.378,2.344),相对偏倚为0.065;在IPTW样本和DRIPW样本中,加权Cox回归分析估计的HR及其置信区间分别为1.725(1.335,2.230)和1.813(1.389,2.366),相对偏倚分别为0.131和0.051。在SMRW样本和DRSMRW样本中,加权Cox回归分析估计的HR及其置信区间分别为1.766(1.365,2.285)和1.830(1.430,2.341),相对偏倚分别为0.093和0.037。在匹配之后的样本中,Cox回归分析估计的HR及其置信区间为1.800(1.394,2.324),相对偏倚为0.062。

表3 各种PS模型对TAC方案组和CAF方案组Cox回归分析

讨 论

双稳健半参模型法作为控制混杂因素的模型,在临床流行病学研究中应用越来越广泛。本研究的主要目的是通过多种PS模型比较对处理效应估计的优劣,其中均衡性诊断是判断模型正确性的一个重要方法。双稳健半参模型法对于PS模型的指定如果正确,那么在匹配、加权之后的样本中试验组与对照组间基线协变量分布应该相同[12]。本文结果表明,在原始数据中TAC方案组和CAF方案组乳腺癌患者的年龄、婚姻状况、肿瘤性质在匹配前不均衡,在匹配、加权之后得到均衡,经过log-rank检验两组生存曲线之间差别有统计学意义(P<0.05),且结果均显示TAC化疗方案治疗乳腺癌的效果优于CAF化疗方案,与赵璐[13-15]等人的研究结果相同。同时,通过对不同模型之间的比较,利用DRIPTW模型和DRSMRW模型得出的处理效应的偏倚显著减小,且减小偏倚的效果优于与之相对的IPTW和SMRW法,同时也优于匹配法和回归调整法,其中DRSMRW模型法最优,相对偏倚为0.037。由本次研究得知,在临床实践中,TAC方案中将蒽环类化疗药物联合紫杉类化疗药物化疗效果更好。

本研究显示,双稳健半参模型法较传统PS法具有明显的优势。第一,该方法是基于PS加权(基于个体的标准化法的边际结构模型),与估计边际效应的PS匹配法相比,适用于数据中包含时依性暴露或混杂变量的研究,也可用于更为复杂的研究设计[8];第二，该方法与回归调整法相比,避免了效应估计时参数过多及共线性的问题所导致的偏倚,易于比较加权调整前后的均衡程度[16];第三，该方法相对于传统分层法而言,其将多个协变量综合为一个均衡分值,将每一观察单位看作一层,避免了协变量较多或存在连续变量时无法解决的过度匹配或过度分层问题[5];第四，该方法不要求试验组的样本量小于对照组的样本量等。此外,仅通过计算一次 PS,就可以构造一个均衡的加权样本,在此样本中能分析多重结局。同时,双稳健半参模型法也存在不足之处:第一，该方法依赖于构造一个加权样本,均衡化原理不如匹配、分层等方法易于理解;第二，该方法对于PS模型错误指定更为敏感[17]等。下一步,我们将继续针对计算PS模型进行比较研究,如利用贝叶斯、随机森林、神经网络等提升双稳健半参模型的稳健性。

综上所述,在回顾性队列研究中对于基线不均衡的生存分析数据而言,随访期较长,混杂或处理(暴露)因素中很有可能包括时依性变量,可采用基于PS的双稳健模型法进行分析,得到类似于RCTs报告中的相对和绝对处理效应结果。因此,双稳健模型法更适用于生存数据的研究。