基于超像素和K-means的图像分割算法
苏建菖 马燕


摘 要: 传统的简单线性迭代聚类(SLIC)超像素算法在图像细节处容易产生欠分割问题,文章对超像素块采用K-means算法进一步聚类,并按聚类中心定义了相似度,对于相似度大于预设阈值的超像素块,视其为欠分割区域,对该超像素块保留K-means聚类结果。实验结果表明,本文算法在分割准确率等各项指标上均优于SLIC算法。
关键词: 超像素; SLIC; K-means; 图像分割
中图分类号:TP317.4 文献标志码:A 文章编号:1006-8228(2019)02-58-03
Image segmentation algorithm based on superpixel and K-means
Su Jianchang, Ma Yan
(The College of Information, Mechanical and Electrical Engineering, Shanghai Normal University, Shanghai 201418, China)
Abstract: The traditional simple linear iterative clustering (SLIC) superpixel algorithm will lead to the issue of under-segmentation in the detail of image. This paper proposes to cluster the superpixel with K-means algorithm, the similarity degree is defined according to the cluster centers. For the superpixel whose similarity degree is greater than the predefined threshold, it will be seen as under-segmentation region and the clustering result of K-means will retain. The experimental results show that the proposed algorithm is superior to the SLIC algorithm with respect to the accuracy of segmentation.
Key words: superpixel; SLIC; K-means; image segmentation
0 引言
近年来,超像素的研究在计算机视觉与图像处理等领域备受关注。通过超像素算法,将颜色相近的像素聚类视为同一区域,从而可进一步降低后期运算的复杂度,该算法通常被用于图像预处理[1],因此超像素算法被广泛应用于图像分割,目标识别,视频分割等计算机视觉领域。
超像素算法能分割出具有一定尺寸的像素块。利用超像素,可以将图像分割成具有语义相同的子块,并且保留对象的边界信息。目前,常用的超像素分割算法主要有Ncut(Normalized Cuts)[2],Mean-shift[3],SLIC[4]等。ACHANTA提出的SLIC(simple linear iterative clustering)算法在召回率、分割准确率、计算存储效率等方面均具有一定优势。但是该方法在图像細节处的分割效果较差,超像素块的分割不准确,不同区域被归类为同一超像素块中,从而会产生欠分割的超像素块。
对于SLIC超像素块欠分割的问题,本文提出一种基于SLIC和k-means的图像分割算法。首先,利用SLIC算法对图像进行初步分割,得到超像素块;接着,对各超像素块分别进行k-means聚类,根据聚类中心定义相似度,并进一步检测属于欠分割的超像素块,对于欠分割超像素块则保留k-means聚类结果。
1 相关算法
1.1 SLIC算法
在SLIC算法中,首先将图像从RGB颜色空间转换到CIE-Lab颜色空间,对应的每个像素的(L,a,b)颜色值和(x,y)坐标位置组成特征空间[L,a,b,x,y],在该特征空间内对所有像素进行聚类,两个像素的相似性可由它们颜色空间的相似度与位置空间的向量距离来度量,相似度越小,距离越大,则相似性越小。根据此项准则,算法具体步骤如下。
⑴ 初始化聚类中心点。SLIC算法首先根据输入参数确定超像素的数目,并以此确定聚类中心数目。算法将依据步长将聚类中心特征向量,i=1,2,3,…,K。N表示图像内所有像素数目,K表示超像素的数目。
⑵ 优化初始聚类中心分布。算法根据所有像素点的Lab颜色梯度,将聚类中心颜色梯度值与其邻域内各像素颜色梯度值进行比较,并将聚类中心移至梯度最小值处,这样就确保初始聚类中心不会在边缘处出现,进一步保证后续分割的准确性。
⑶ 计算像素点与聚类中心的距离D。这一步骤类似k-means算法,通过不断迭代计算每个像素点到聚类中心的距离D,将每个像素点归类为距离最近的聚类中心。
像素点到聚类中心的距离D公式定义如下:
⑴
⑵
⑶
其中,j表示第j个像素点,i表示第i个聚类中心,dc和ds分别表示颜色距离和坐标距离,Ns为类内最大空间距离,可以将Ns设置为步长S,且Ns=S,Nc为最大颜色距离,随图像不同而不同。
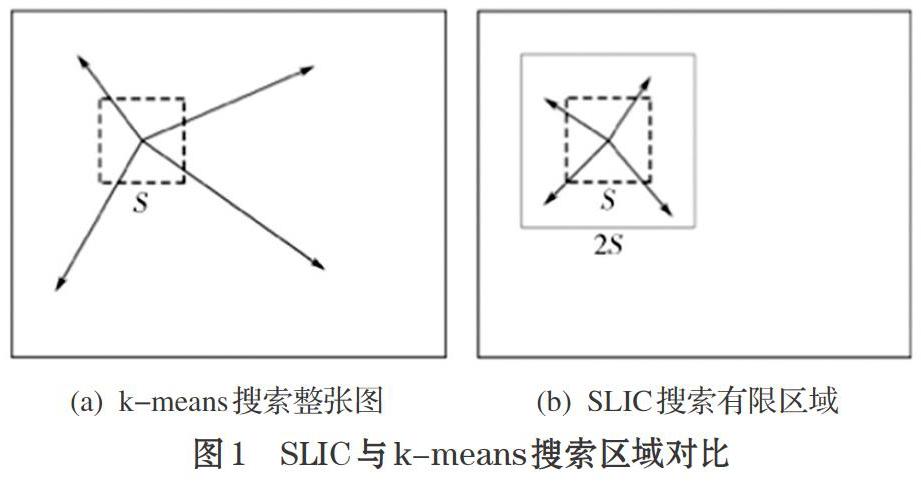
与k-means不同的是,SLIC算法只在每个聚类中心的2s×2s邻域内计算像素点与聚类中心的距离,而k-means算法则不需要界定距离,即在全局内搜索。图1列出了SLIC与k-means在搜索范围上的区别。
⑷ 像素点分类。根据最小距离准则,将像素分类至距离最小的聚类中心,并再次迭代上述过程更新聚类中心,直至达到最大迭代量或聚类中心不再变化。
⑸ 聚类优化。利用连通性,将多连通、区域面积过小等区域与相邻区域合并。至此图像被分为多个超像素像素。
1.2 k-means算法
k-means聚类是无监督学习的一种典型的聚类算法,其主要任务是将图片分为多个类或簇,同一簇内的像素相似度尽可能大,而不同簇间的像素相似度尽可能小。k-means聚类通常通过欧式距离计算相似度。该算法具体如下:
⑴ 随机从图片中选取K个点作为初始聚类中心;
⑵ 计算图片上所有像素到聚类中心的距离,把像素归到离它最近聚类中心所在的类;
⑶ 计算新形成的每一个聚类像素的平均值,更新得到新的聚类中心;
⑷ 更新迭代直至聚类中心不再变化,则聚类函数已收敛。
2 改进SLIC算法
在传统的SLIC算法中,有的超像素块分割不够完全,如图2绿色圈中区域所示。为解决SLIC算法的欠分割问题,本文对欠分割区域进行再聚类,以得到更精细的分割效果。
⑴ 在超像素内选取k-means聚类中心。
k-means算法的缺点之一是需要预先给出簇总数k,并且难以估计。本文算法取K=2对每个超像素块进行k-means聚类,颜色空间为RGB颜色空间。假设有个超像素,则总共需进行m次k-means聚类。进行k-means聚类后重新计算并获取超像素块的聚类中心Ci,Cj,其中Ci,Cj的值分别表示[Ri,Gi,Bi],[Rj,Gj,Bj]。
⑵ 计算超像素内的两类相似度。对已进行k-means聚类的超像素区域在RGB颜色空间内采用欧式距离计算两类相似度dRGB,公式表示如下:
⑷
对于dRGB>ξ的超像素,则认为该超像素欠分割,可以进一步分割,则将k-means聚类结果作为分割结果。这里,ξ为预设阈值,经大量实验,本文设置阈值ξ=280。欠分割区域如图3所示,天空与树枝被分配到同一个超像素内。
⑶ 对欠分割的超像素重新标定类别。在对超像素执行k-means聚类时选择k=2,聚类后得到0,1两种标签,分别用红色与蓝色表示两种类别。若超像素块内有两种颜色,则表明该超像素已进行聚类再分割。
3 欠分割超像素处理结果
使用本文算法对图2所示图像进行超像素分割,结果如图4所示。图中欠分割区域已全部进行区域聚类后再分割,分割精细度高,效果良好,且在分割良好区域保留了SLIC的原始分割结果。树枝与天空融合的超像素已被再分割为两类。
欠分割区域再分割效果如图5所示,对于同一超像素内的树枝与天空背景进行了准确分割。
4 实验结果和分析
将本文算法与SLIC算法进行了对比实验,其中采用基于分割区域、基于分割边界的评价指标的评价指标如下[5]。
CUE(Corrected Undersegmentation Error):CUE是基于分割区域的评价指标,反应人工分割结果与超像素分割结果重合度。其计算公式如下:
⑸
其中sk是第k块超像素,gi是第块人工分割区域,gmax(sk)为与人工分割区域的最大重叠面积,定义式如下:
⑹
基于分割边界的评价指标主要是边界召回率BR(Boundary Recall):该指标用来体现超像素分割与人工分割边界的吻合度,算法的边界召回率越高,表示其生成的分割边界与真实边界越接近,其计算公式如下:
⑺
B(s)表示人工分割的轮廓集,B(g)表示超像素分割结果。p为人工分割轮廓线上的点,q为超像素分割轮廓线上的点,I[·]函数用于确定超像素轮廓中在距离内是否存某点与当前人工分割轮廓的上的点p(ε=2)。
使用本文算法得到的分割结果与传统SLIC算法进行對比,各项指标结果如图6所示。从中可见,本文算法在各项指标上均优于传统SLIC算法。
为了验证本文算法的运算效率,分别在超像素数量K取不同值的情况下与传统SLIC进行对比。实验结果见表1。从表1可见,本文提出的新算法与传统SLIC算法相比运行时间较慢,但综合分割准确率与运行时间考虑,本文提出算法在整体运行效果上要优于传统SLIC算法。
5 结束语
本文针对传统SLIC算法存在的欠分割现象提出了区域聚类再分割算法。本文实现提出的新算法在不改变原始SLIC分割结果的情况下取得更准确的分割结果。该方法在运行时间上略高于传统SLIC算法,今后将在研究工作中继续优化该算法。
参考文献(References):
[1] Hsu C Y, Ding J J. Efficient image segmentation algorithmusing SLIC superpixels and boundary-focused region merging[C]// Communications and Signal Processing.IEEE,2014:1-5
[2] Shi J, Malik J. Normalized Cuts and Image Segmentation[J].IEEE Trans.pattern Anal.mach.intell,2000.22(8):888-905
[3] Comaniciu D, Meer P. Mean shift: a robust approachtoward feature space analysis[J]. IEEE Trans Pattern Analysis & Machine Intelligence,2002.24(5):603-619
[4] Achanta R, Shaji A, Smith K, et al. SLIC superpixelscompared to state-of-the-art superpixel methods.[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence,2012.34(11):2274-2282
[5] 叶伟,王远军.基于Mumford-Shah理论的最小生成树图像分割方法[J].计算机辅助设计与图形学学报,2009.21(8):1127-1

