武汉地铁第三轨受流器动态接触力测量模型及参数标定

阮 杰 刘子知 闫晓晖 吴继成 徐鸿燕

(1.武汉理工大学现代汽车零部件技术湖北省重点实验室，430070，武汉；2.武汉地铁运营有限公司，430035，武汉；3.中铁第四勘察设计院集团有限公司电化处，430063，武汉//第一作者,讲师)

第三轨受流器动态接触力的变化情况直接影响轨道车辆受流质量的高低[1]。受流器滑靴所受的载荷随第三轨激励而不断发生变化，滑靴与第三轨之间有较大电流通过，加上第三轨表面硬点对滑靴产生的冲击，使得受流器与第三轨之间的接触情况十分复杂，其接触力无法直接测得[2]。因此，需要通过设计开发第三轨受流器动态接触力测量装置来间接测量靴轨动态接触力。

接触力的间接测量方案和参数标定直接决定动态接触力测量结果的准确性和有效性，而目前我国对此研究较少。文献[3-6]在对铁路车辆第三轨与受流器之间的接触压力和动态响应进行测试的过程中，使用应变片对受流器滑靴的接触压力进行测量，但并未对等效惯性质量进行计算或标定。

本文设计了使用应变片和加速度传感器对第三轨受流器动态接触力进行检测的测量方案，通过静力学和动力学的理论建立了靴轨动态接触力与应变值和加速度值的计算关系式，最后设计了受流器静态和动态标定试验，并获得了上述计算关系式中的相关参数。

1 第三轨受流器动态接触力测量系统方案

1.1 受流器结构

以武汉地铁某线列车使用的某型下接触式受流器(以下简为“受流器”)为研究对象，该受流器由固定部分、摆动部分、转轴和弹簧组成。其中固定部分包括安装底座和阻尼减震器；摆动部分包括摆臂、滑靴支座和滑靴。受流器三维模型如图1所示。

1.2 测量系统方案

由受流器的结构可知，当受流器处于工作状态时，第三轨对滑靴的压力会使受流器摆臂产生一定的弯曲变形。因此，可以通过在受流器摆臂表面粘贴应变片传感器来间接测量受流器和第三轨之间的接触压力。惯性力部分可参考已有弓网动态力测量方法，即使用加速度传感器进行测量，安装位置为振动幅度较大的滑靴支座中心位置。受流器简化模型与测量方案如图2所示。该方案配合使用应变片传感器和加速度传感器来间接测量受流器和第三轨间的动态接触力。

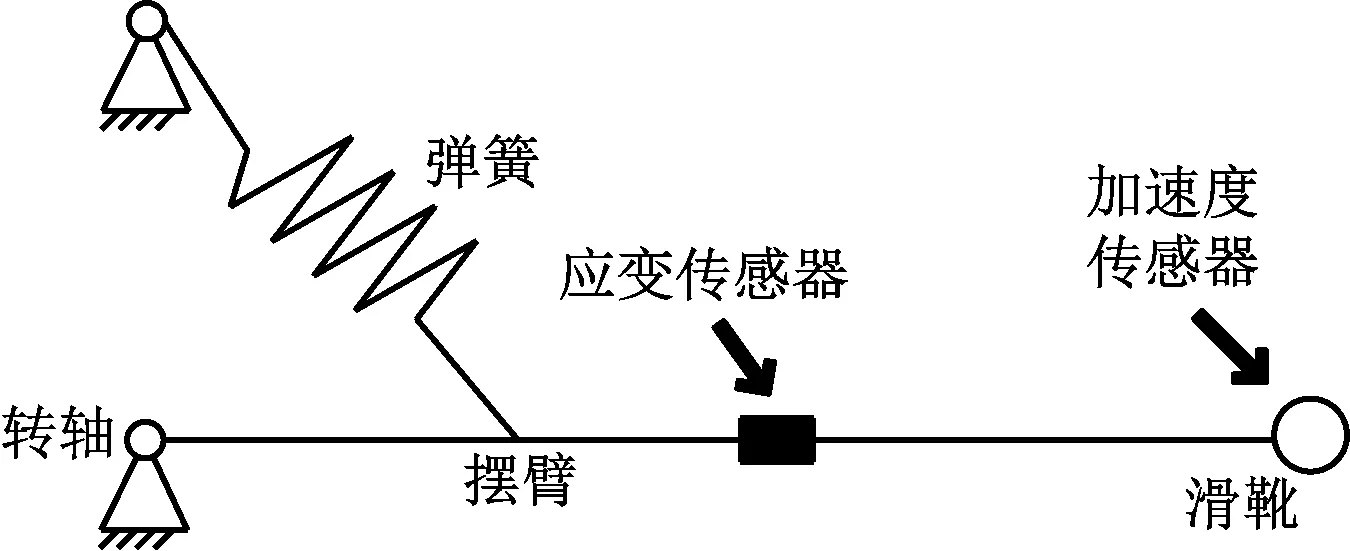
图2 受流器简化模型与测量方案

1.3 应变片布置位置的确定

应变片布置位置的选择需考虑以下因素：①表面平整，且便于应变片粘贴牢固；②应变变化平缓；③工作中能产生足够大的应变值。

参考目标受流器的安装说明书，第三轨与受流器的静态接触压力为120 N±24 N。取120 N作为靴轨静态接触压力，由有限元分析结果可知，摆臂表面的应变值随着摆臂到弹簧安装孔轴线距离的缩小而逐渐变大，距离弹簧安装孔轴线10～30 mm处的摆臂表面应变值的数量级为(10-5～10-4)ε0(ε0为应变)。该数量级符合电阻应变片的测量灵敏度要求。最终选择距离滑靴支座中心线95 mm处的摆臂截面作为应变片横向中心截面。

2 第三轨受流器测量模型理论分析

2.1 静力学分析

在滑靴上表面中心施加静力载荷，并对受流器简化结构进行受力分析，如图3所示。设滑靴中心到应变片中心的距离为L，滑靴中心到转轴轴线的距离为L1，应变片中心到转轴轴线的距离为L2。对滑靴上表面施加静力F，受流器摆臂绕转轴向下的转动角度为θ。

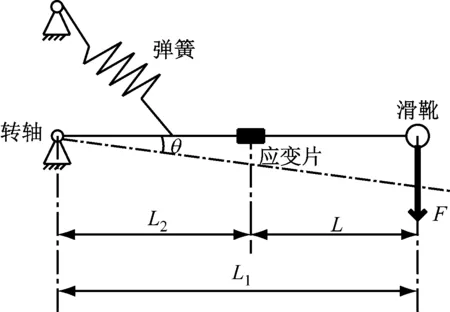
图3 受流器结构受力示意图

当发生横力弯曲时，弯矩随截面位置变化而变化。一般情况下，在形状规则的同一截面上，最大应力发生于离中性层最远处。应变片粘贴中心处摆臂截面几何形状近似为矩形，则应变片中心截面弯矩M和摆臂表面应变ε成正比关系，即：

M=WEε

(1)

式中：

W——抗弯截面系数;

E——摆臂杨氏模量。

由此可得ε和F的关系为：

F=WEε/L

(2)

设比例系数k为：

k=WE/L

(3)

则有：

F=kε

(4)

其中，k可以采用静态标定试验得到更为精确的结果，且采用数值计算得到的k可以和由静态标定试验得到的比例系数ks作对比分析。

2.2 动力学分析

受流器摆臂和滑靴因承受动态压力而产生的振动必然会伴随加速度和惯性力，因此需要对受流器进行动力学分析。建立滑靴动态载荷与摆臂表面贴应变片中心处的应变值和滑靴中心点的加速度之间的关系式，为后续受流器的动态标定试验和对比验证提供理论依据。

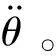
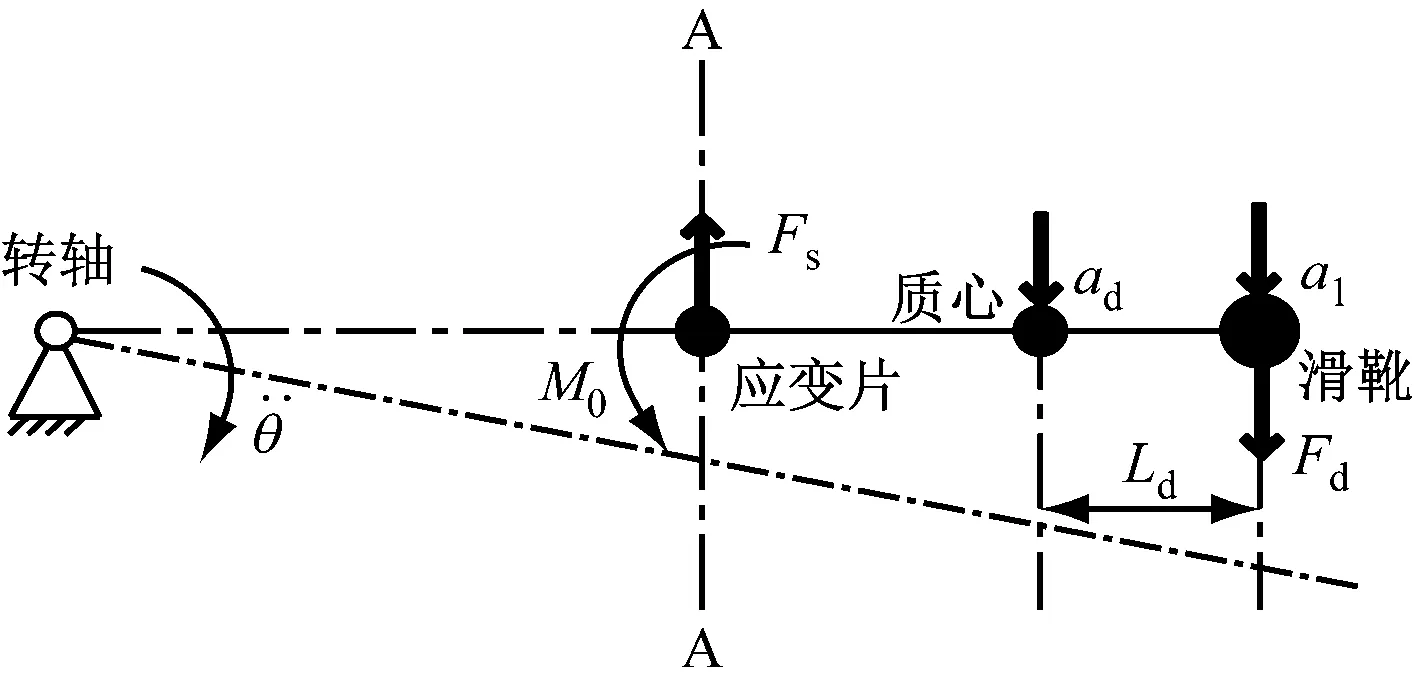
图4 动载作用下受流器局部受力示意图

(5)

(6)

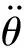
ad/a1=(L-Ld)/L1

(7)

(8)

结合静力学理论分析结果,可得Fd表达式：

(9)

设右段摆臂等效质量为me，则：

me=[Id+md(L-Ld)×(L1-Ld)]/(L/L1)

(10)

由静力学分析可知，kd为常数，则式(9)可简化为：

Fd=kdε+mea1

(11)

3 第三轨变流器动态接触力测量系统参数标定

3.1 受流器静态标定试验

将受流器底座用螺栓安装在固定支架底板上，如图5所示，把摆臂调整到与X轴平行的位置后将转轴锁死，在受流器滑靴支座中心位置下部悬挂砝码钩。通过增减标准砝码，给受流器提供静态载荷。在测量截面上、下表面分别粘接2片相同的应变片，并按全桥方式连接到应变仪。

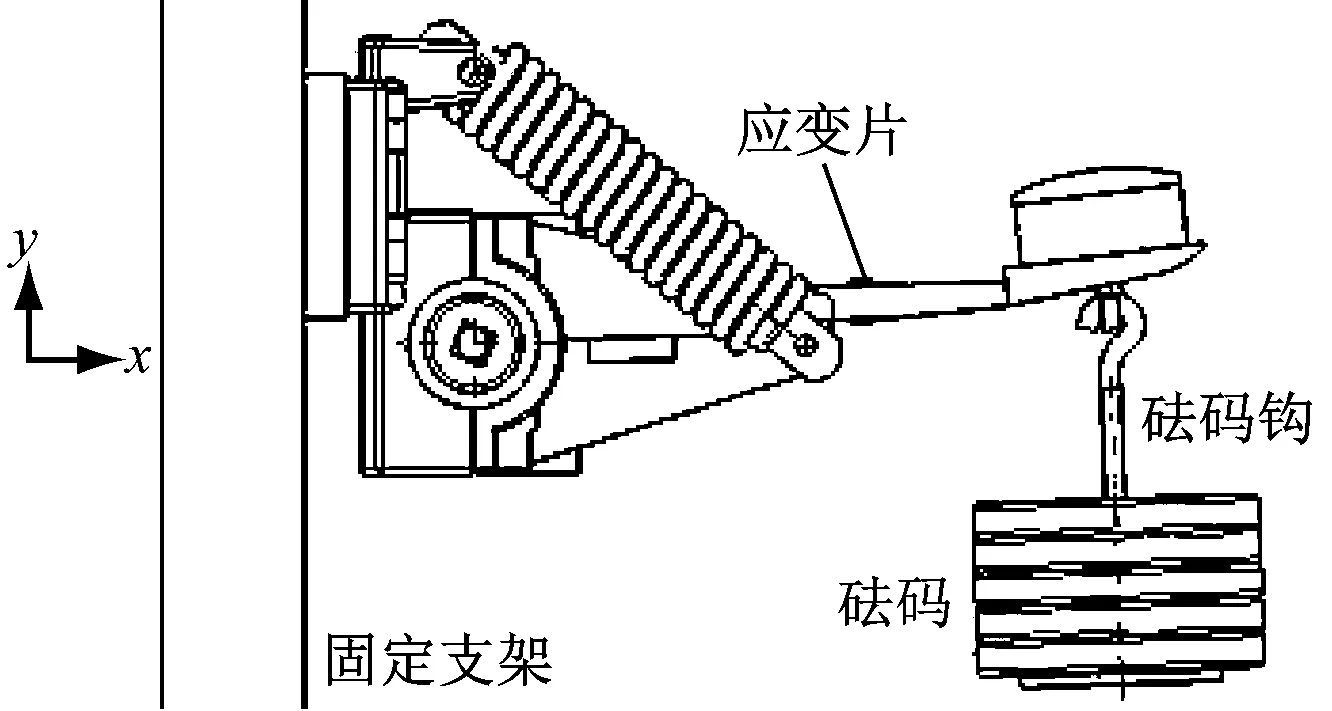
图5 静态标定试验装置

测量时，在砝码钩托盘上逐块加载砝码，通过DH 5922数据采集仪测量应变值。在加载和减载两种情况下各测量两组数据，并求得4次测量应变值的平均值。

对静态载荷数据与平均应变值进行线性拟合分析，即可得到受流器摆臂应变片的应变与滑靴中心所承受静态载荷之间的比例系数，如图6所示。

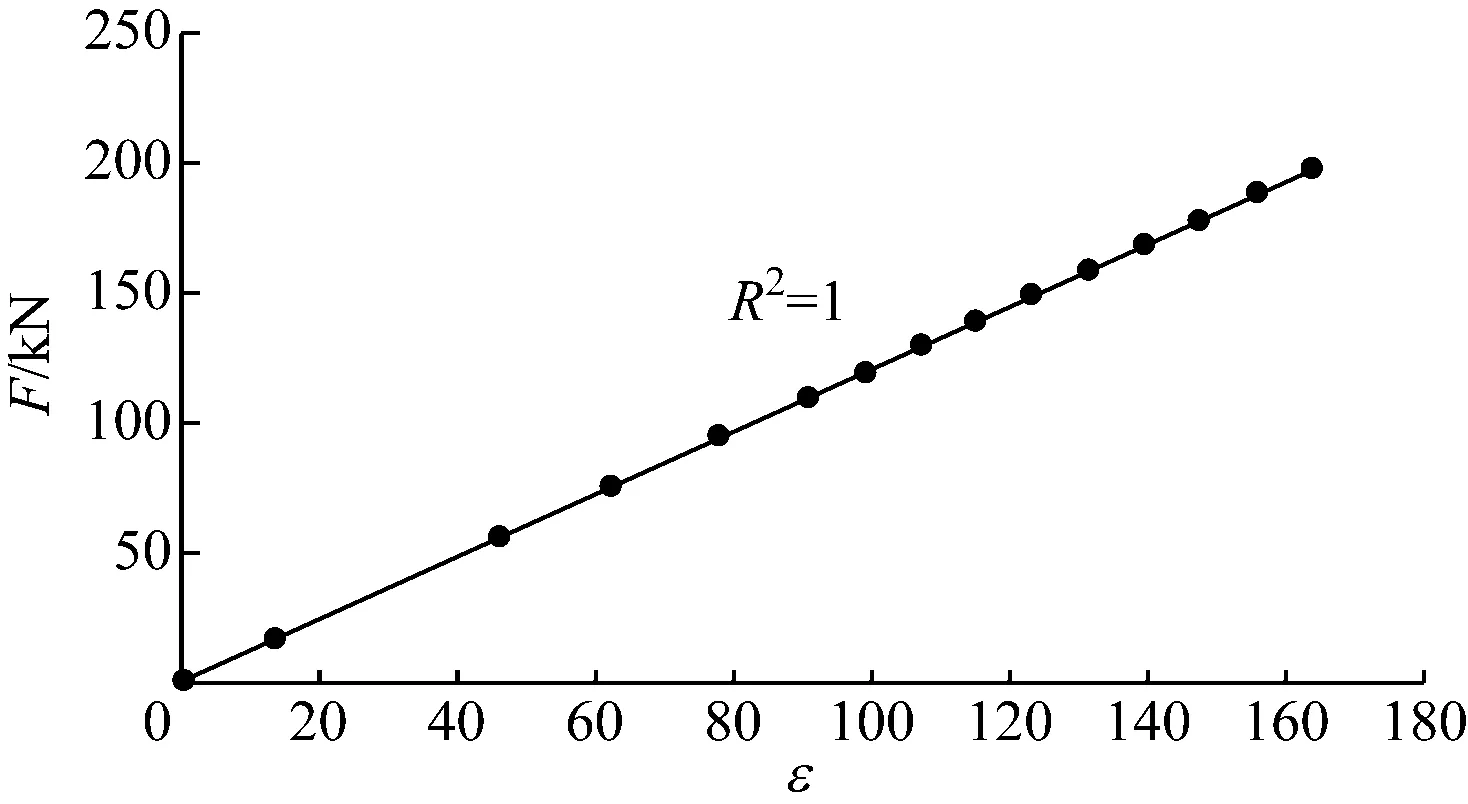
图6 静态标定线性拟合分析图

进行线性拟合后得到的结果如下：

F=1.208 8ε-0.115

(12)

式(12)中，0.115为摆臂重量修正值。由图6线性拟合分析得到线性相关度R2为1，表明F与ε之间的线性度极高。由静态标定试验测得比例系数ks为1.208 8。

3.2 受流器动态标定试验

由于受流器弹簧为拉伸弹簧，在滑靴支座不受力时处于压缩状态而不能产生受迫振动。因此，在滑靴支座正下方通过螺栓和转接板刚性固连20 kg砝码将受流器弹簧拉开，如图7所示。动态标定试验将使用激振器使滑靴支座在激振力作用下带动摆臂绕转轴产生受迫振动。力传感器下端通过顶杆1和激振器可动部件相连，且其上端与顶杆2相连。将激振器底座调整到合适高度并转动转轴使顶杆2轴线对准砝码中心轴线，将顶杆2与砝码下端通过转接螺母相连。将力传感器的输出信号接入DH5922仪器通道，并在软件中分别设置好应变片、加速度计和力传感器3个通道的参数。

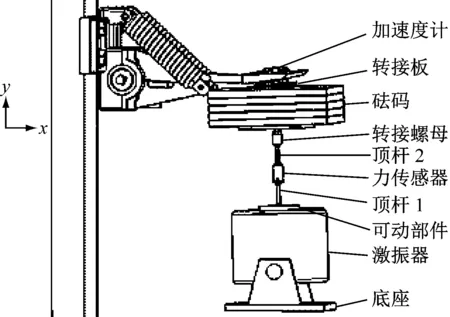
图7 动态标定试验装置

根据图7中的动态标定试验装置，将建立的受流器三维模型去掉滑靴部件，并在滑靴支座下方根据砝码实际尺寸建立与滑靴支座固连的砝码模型，并在CATIA(计算机辅助三维交互应用)软件中测量其质量、质心位置和绕X轴对质心的转动惯量，代入式(9)可得固连砝码的右段摆臂等效质量理论计算值mo,c为22.3 kg。

将DH5922动态数据采集仪的采样频率设为5 000 Hz。并依次设定信号发生器的频率为10.2 Hz、15.2 Hz、19.9 Hz、23.7 Hz、30 Hz、35.3 Hz、40 Hz、47.8 Hz、60 Hz、66 Hz、70 Hz、90 Hz和110 Hz,通过观察力传感器通道显示的动态数据极值，在每种频率下将激振力的幅值调整为15 N、30 N、45 N、60 N和75 N，其中激振力均为随时间变化的正弦曲线。

由试验测得的加速度和应变亦近似视为随时间变化的等幅正弦曲线。为节省计算量，分别求取每组数据中加速度和应变的最大值和最小值，从而求出a1和ε。由式(11)可知，在动态标定试验中，固连砝码右段摆臂的等效质量mo,e为：

mo,e=(F-1.208 8ε)/a1

(13)

分别采集每种频率下对应不同力幅值的5组动态数据。每组动态数据均包含加速度计、应变片、力传感器随时间变化的参数信息，采集时间大约为5 s。对测试数据进行整理及计算，如表1所示。表1中：mo,ave为同一频率下5个等效质量测量值mo,e的平均值；mo,max和mo,min分别为同一频率下5个等效质量中的最大值和最小值；(mo,max-mo,min)/mo,ave为相对极差，用于分析每一频率同激振力幅值下mo,e的离散程度；(mo,c-mo,ave)/mo,c为数值计算差值，用于对mo,c与mo,ave的差值进行分析。

根据表1，将mo,e的计算数据绘制成三维图，如图8所示。

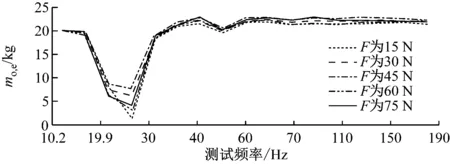
图8 固连砝码右段摆臂的等效质量

由图8可知，当测试频率为19.9 Hz和23.7 Hz时,右段摆臂的等效质量明显降低；当测试频率为47.8 Hz时,等效质量略有降低;在其他大部分测试频率范围内等效质量趋于恒定，且与mo,c较为接近。

将固连砝码的受流器有限元仿真模型导入ANSYS软件中进行模态分析，获得前5阶模态固有频率。由模态分析结果可知，固连砝码的受流器在23.2 Hz及46.2 Hz附近发生共振，这与理论计算时摆臂的刚体假定不一致，导致上述频率附近动态标定数值出现偏差。

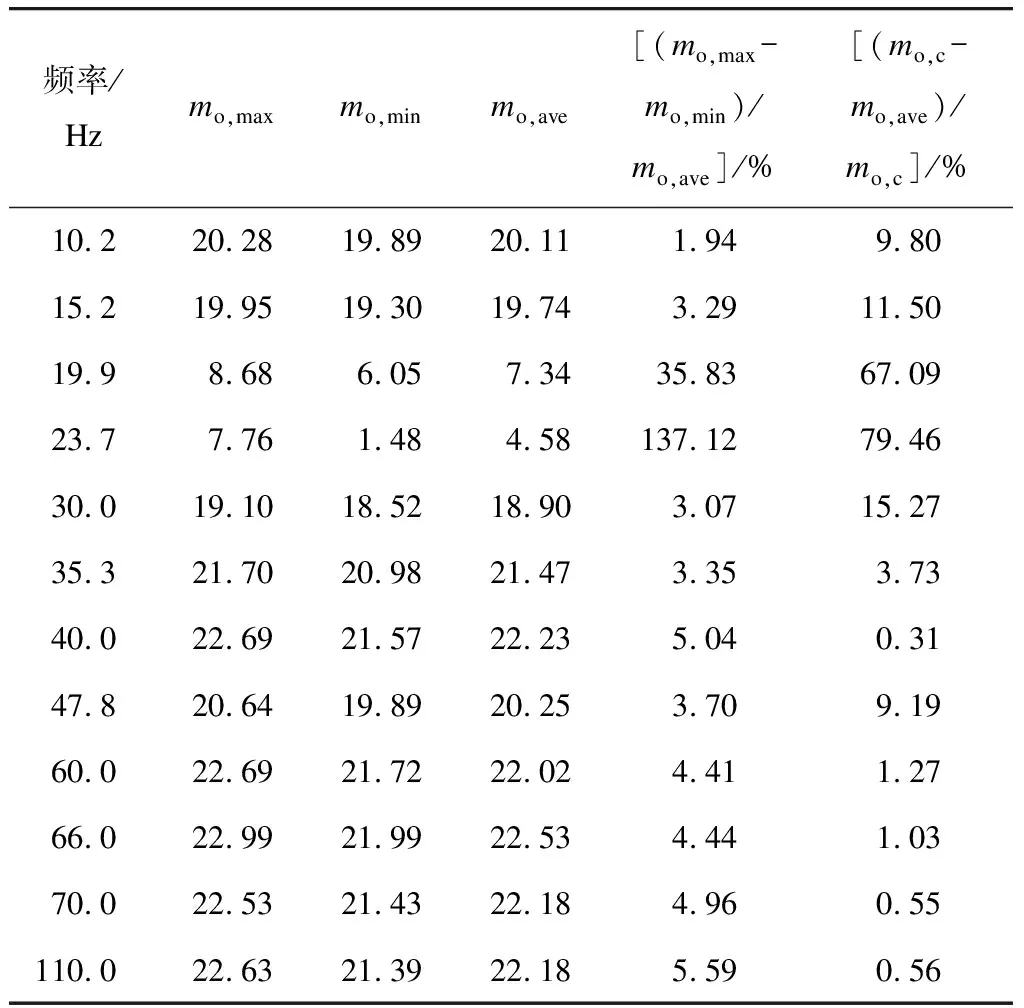
表1 动态标定实验测试数据分析

因此，由数值计算差值可知，在23.2 Hz±13 Hz的1阶固有频率范围内，等效质量数值计算值与试验标定平均值差值较大，而在其他频率下二者差值均在10%以内，且相对极差较小，进一步验证了模型的精确性以及试验的合理性。

3.3 受流器测量方案等效质量的计算

将受流器三维模型沿应变片横向中心截面截成两部分，在CATIA中测得各项参数，代入式(9)可得到刚体的右段摆臂等效质量数值计算值为2.585 kg。对去除挂载砝码的受流器模型进行模态分析，获得其1阶固有频率为118.5 Hz，远大于受流器动态接触力测量频率，证明了等效质量计算结果有效。

4 结论

本文通过设计第三轨受流器动态接触力的测量模型及参数标定试验，得到如下结论：

(1) 设计了第三轨受流器动态接触力测量方案，并根据有限元应变分析确定了应变片的安装位置。

(2) 通过静力学理论分析确定了滑靴表面压力与摆臂表面贴应变片中心处应变值的线性关系。通过动力学理论分析建立了滑靴动态载荷、应变值和滑靴中心点加速度之间的关系式。

(3) 通过静态标定试验获得受流器摆臂表面粘贴应变片位置的应变与滑靴中心所承受静态载荷之间的比例系数。通过动态标定试验获得固连砝码的右段摆臂等效质量，并与模型计算结果进行对比，验证了测量模型和等效参数的精确性。