从最佳出售价格角度选择商业地产经营模式——自持还是出售

(武汉大学经济与管理学院 湖北 武汉 430072)

一、引言

房地产项目对于开发商来说是投资盈利的工具,厂商是追逐利益的，开发商做决策的出发点是最大化利润。房地产开发的项目主要包括商业项目和住宅项目。商业地产项目主要是指用于商业用途的房地产产品，主要包括超市、购物中心，商业广场、酒店和商业街区等多种业态类型。

商业地产项目在房地产开发企业的业务中占有重要地位，与住宅项目不同，房地产开发商对待商业地产项目一般有两种处理方式：一种是与住宅项目一样直接销售出去；另一种是选择自己持有运营，通过租金获取利润。两种处理方式各有优点：直接销售资金回流速度快，资金压力小；选择自持、通过租金获利，可以获得持续回报，从长期来看利润丰厚，且可以拓展开发商的业务类型，增强企业发展的可持续性。

面对这样的双重选择，如何做出正确的决策就显得十分重要。由于房地产开发的周期比较长，从项目筹备到项目建成至少需要3-4年的时间，这样就使得地产商做出决策之前要首先对未来商业的销售价格有一个合理的预期，当出售问题被考虑时，通过比较当前地产项目的市场价格与最优出售价格，做出是否出售的决策。即在不确定性条件下，从投资的最优价格入手，在实物期权的框架下研究房地产开发商对商业地产的经营决策：是自持出租还是直接销售？

二、模型建立

(一)商业地产项目的价格模型

商业地产项目的价格P服从几何布朗运动，即价格P满足下式：

dP=μPdt+σPdz

(2.1)

变量μ为商业地产价格P的收益率期望值，变量σ2为商业地产价格的方差。变量z为维纳过程。dz表示维纳过程的增量，满足：

(2.2)

即dz服从均值为0,方差为dt的正态分布。对于P，可以证明满足下列表达式：

(2.3)

μ为开发商在短时间段内获取的收益期望值，多数投资者在承担更大风险是会要求更高的预期收益，故变量μ依赖于商业地产价格的风险。它的取值与经济体系中的利率水平也有关，利率水平越高，投资者对给定的商业地产项目的预期收益也会越高。

(二)商业地产项目决策的利润函数

如果房地产开发商决定在时刻t出售商业地产项目，那么他将获得利润Pt-C，其中C表示商业地产项目的开发成本，这一成本对任何一个开发商来说是相同的。由于时间t是连续的，故将利润用连续复利贴现因子e-ρt贴现到零时刻，则利润函数可表示为：

V(P,t)=e-ρt(Pt-C)

(2.4)

上式表示在t时刻将商业地产项目出售所获得的利润的现值。此处的ρ需满足ρ>μ，否则选择一个较大范围的时间t，满足式(2.3)的P可能会无穷大，在这种情况下，只要等待总能有更好的投资机会，则不存在最优解。

三、模型求解

由Ito引理可知，关于商业地产价格P和时间t的函数V(P,t)遵循下列过程：

(3.1)

式(3.1)具有下述积分意义：

(3.2)

对式(3.2)两边同时作期望算子Et，并取其最大值，得：

(3.3)

(3.4)

(3.5)

(3.6)

由上文的模型设定知

V*(P,t)-V(P,t)=0

(3.7)

进一步得出

(3.8)

(3.9)

由模型设定知式(3.9)的解的形式为V(P*,t)=e-ρt(P*-C)，设上式的解为：

V(P,t)=e-ρtQ(P)

(3.10)

将式(3.10)代入式(3.9)，得：

(3.11)

将求P*的目标函数明确写为下列待解方程

(3.12)

由目标函数(3.12)的形式推测该式有形如Q(P)=APa的解，将其代入式(3.11)，得

(3.13)

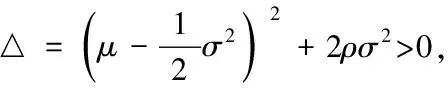
(3.14)

(3.15)

由目标函数(3.12)知Q、Q的一阶导数和Q的二阶导数均为线性的，所以Q的一般解可以看做任意两个独立解的线性组合，可用a1和a2的线性组合表示为：

Q(P)=A1Pa1+A2Pa2

(3.16)

(3.17)

解得：

(3.18)

其中

(3.19)

同时将A1和P*的表达式代入Q(P)=A1Pa1，得到

(3.20)

且根据P*的定义有P*=Pτ*，故

(3.21)

P*会随着a1的增大而减小。

四、结论

本文以实物期权模型为基础，在连续时间背景下，建立了房地产开发商在面对如何处置商业地产项目的问题时决策的基本模型。

本文的创新之处在于将开发商选择已开发完毕商业地产的经营模式的决策过程模型化。一般房地产企业会因市场下行或者获得流动性资产而急于出售商业地产，忽略了商业地产的期权价值；或者简单地认为“放长线钓大鱼”是最优决策，会选择一直持有自营。其实由于商业地产项目具有较大的灵活性，开发商对其可以通过多种方式最大化其收益。本文建立了以实物期权模型为基础的决策模型，帮助企业在商业地产经营模式的选择上更加理性。