基于组合模型的厦门港集装箱吞吐量预测

汪 强，刘晓佳，闫长健，张 荀

(集美大学航海学院，福建 厦门 361021)

0 引言

近几年来，厦门港集装箱运输快速发展，港口集装箱运输总体呈上升趋势，2017年，厦门港集装箱年吞吐量突破107TEU。随着海上丝绸之路的开辟，中欧班列的开通，全国第一个全自动化码头的建立，厦门港集装箱运输面临新一轮的机遇与挑战。

集装箱运输是一个地区经济发展的重要组成部分，准确预测未来集装箱吞吐量不仅能为该地区经济发展规划提供有力的数据支撑，而且能够为集装箱运输所带来的环境影响提供可靠的数据分析。厦门港的集装箱吞吐量仍处于中等水平，历年集装箱吞吐量数据量少，影响数据发展要素权重不明确。目前对集装箱吞吐量的预测方法有：时间序列法、灰色理论和BP神经网络。时间序列预测虽然能消除原始时间序列的波动性问题，但是未考虑到因偶然因素而产生的随机性问题[1]。灰色理论包括GM(1,1)、灰色Verhulst和灰关联分析等，主要用于研究数据少、信息贫的不确定性问题，但对于波动性较大的振荡序列往往存在精度不高，预测结果存在偏差较大等问题[2]。BP神经网络模型对初始网络权重非常敏感，作为预测模型时，需要大量的原始数据进行训练[3]。由上述分析可知，单独使用一种方法并不能很好地解决“样本小、信息贫”的时间序列预测问题。因此，本文将灰色理论与马尔科夫状态转移预测方法相结合，先利用灰色Verhulst模型对原始时间序列进行预测，再利用相对误差修正方法对模型进行有效改进。最后，通过马尔科夫模型判断相对误差状态，对预测值进行修正。

1 灰色Verhulst-马尔科夫模型的建立

1.1 灰色Verhulst模型

灰色Verhulst对原始数据呈“S”型发展，先稳定上涨，随后下降，最后保持稳定增长水平的序列预测有较高的模拟精度[4]。

设一段原始非负时间序列为：

X(0)={x(0)(1),x(0)(2),…,x(0)(n)}，

(1)

X(1)={x(1)(1),x(1)(2),…,x(1)(n)}，

(2)

X(1)为X(0)的1-AGO序列，即

(3)

Z(1)为X(1)的紧邻均值生成序列：

Z(1)=(z(1)(2),z(1)(3),…,z(1)(n))，

(4)

Z(1)(t)=(x(1)(t)+x(1)(t-1))/2,t=2,3…n，

(5)

称X(0)+aZ(1)=b(Z(1))2为灰色Verhulst模型，其中a和b为参数。

d(x(1))/dt+ax(1)=b(x(1))2

(6)

(7)

时间响应函数为：

x(1)(t)=ax(1)(1)/(bx(1)(1)+(a-bx(1)(1))eat)。

(8)

原始序列的预测值为：

(9)

1.2 马尔科夫预测模型

马尔科夫预测模型对某个系统今后所处的状态仅与目前所处的状态有关，与过去系统所处的状态无关，即为无后性。并且马尔科夫预测模型对一段波动性明显的无后效时间序列进行预测时，优势明显，主要可划分为以下三步[5]。

1)状态划分 利用灰色Verhulst预测结果与实际数据之间的相对误差，根据其相对误差大小将其平均分成若干个状态区间[6]。

2)计算概率转移矩阵 根据各年预测的相对误差的大小，分别落入不同的状态区间的结果，计算步长为n的状态转移概率矩阵R(n)。

3)改进预测值 通过灰色Verhulst预测结果与实际数据之间的相对误差大小，将其平均划分为j状态区间[wj-,wj+]，wj-,wj+分别表示j状态区间的上下确界，取相对误差状态区间的中值作为灰色预测的修正值，

(10)

其中：当预测值比实际值高估时，分母中的正负号取正值；当预测值比实际值低时，分母中正负号取负值；当预测值与实际值比较相近时，不用修正；无法比较时，取负值[7]。

1.3 组合模型

灰色Verhulst模型可对中长期的时间序列进行预测，但存在精度不高问题。马尔科夫模型可针对模型相对误差波动性明显的序列进行改进，提高预测精度。

本文提出先使用灰色Verhulst模型对厦门港集装箱序列进行预测，然后采用马尔科夫模型对其预测结果的相对误差进行修正，完成两种模型的组合。

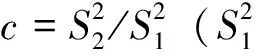
当所建模型的分级标准为四级(p<0.75,c>0.65)时，一般不能用该模型进行预测。

2 厦门港集装箱吞吐量预测

2.1 灰色Verhulst预测

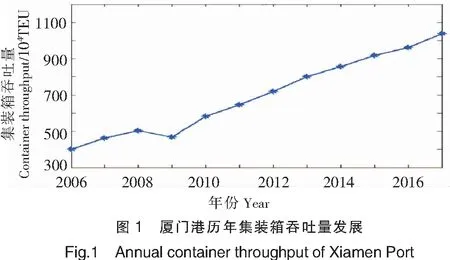
厦门港全年集装箱吞吐量2000年首次突破106TEU，2017年，突破107TEU。选用(2006—2017年)厦门港集装箱吞吐量数据[注]数据来源：http://www.chinaports.com/ports，建立灰色Verhulst初始时间序列，如图1所示。

通过图1可发现，厦门港集装箱历年增长呈“S”型趋势，先增长后下降再保持持续增长，总体呈上升趋势，因此选用灰色Verhulst模型进行预测。

根据式(1)～式(10)计算得灰色Verhulst相应数据如下：

BTB=

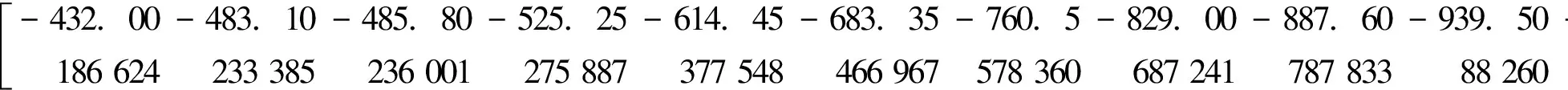
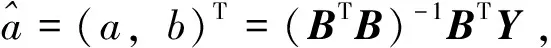
灰微分方程：d(x(1))/dt-0.140 271x(1)=-0.000 076(x(1))2。

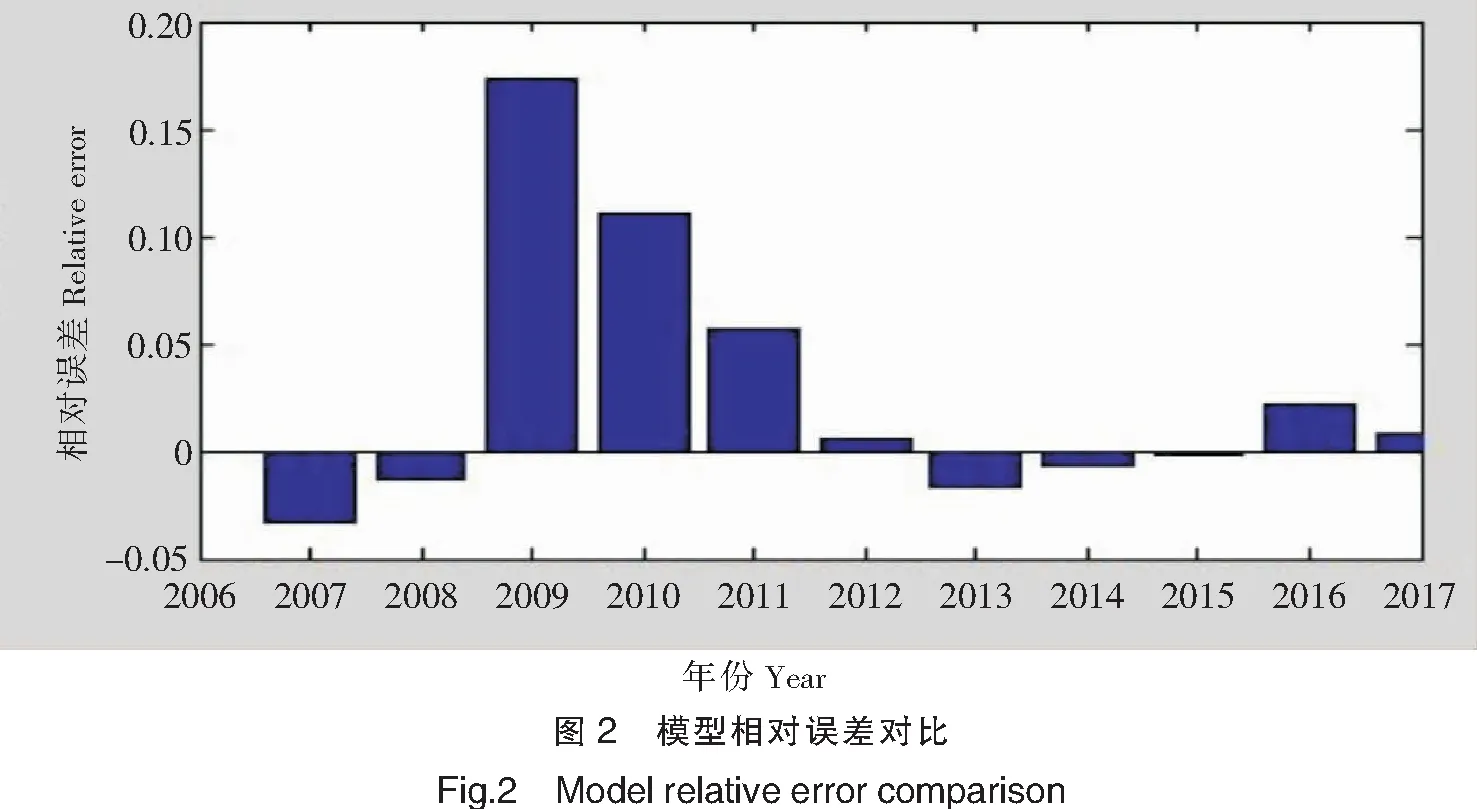
根据式(1)～式(9)计算得灰色Verhulst预测结果如表1所示，相对误差波动如图2所示。由表1可看出灰色Verhulst预测实际值与模拟值的残差序列仍较大。计算得灰色Verhulst预测平均相对误差为3.74%，精度不高，需要改进。因此引入马尔科夫模型修正相对误差序列，改进预测结果[9]。

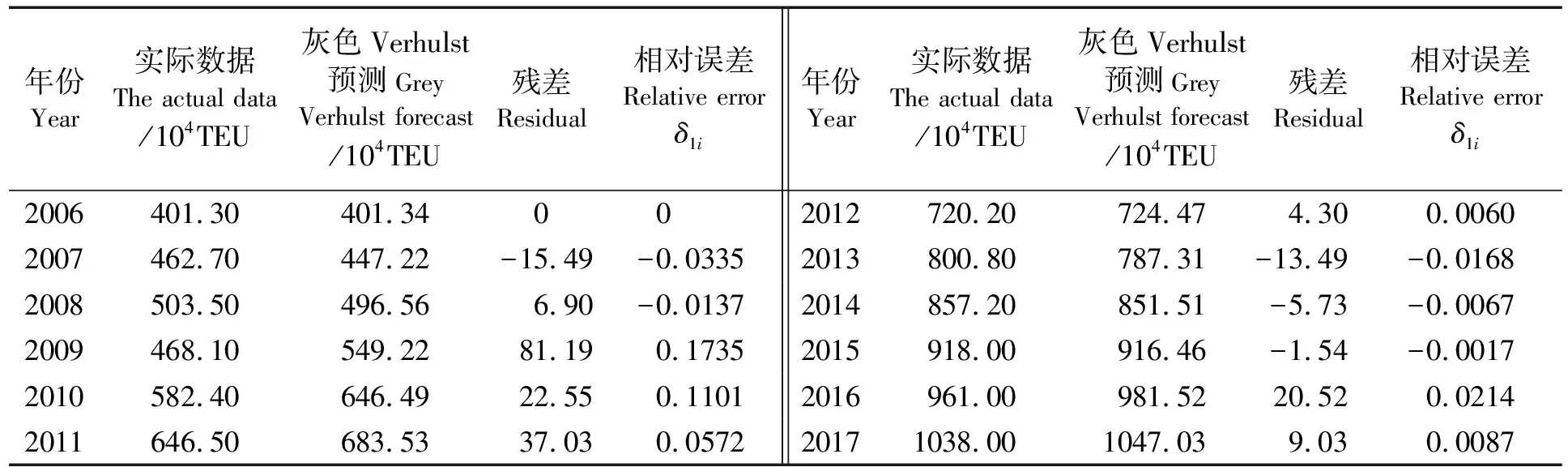
表1 模型数据对比

2.2 马尔科夫修正

根据预测的相对误差大小划分状态区间，因为预测值与实际值的相对误差波动较大，因此在状态划分时，应尽量考虑状态多一些[10]。这里划分为5个状态wj(j=1,2,…,5)，结果见表2。

表2 相对误差状态划分区间

由相对误差状态区间及初始状态划分计算马尔科夫模型的一步转移概率矩阵R(1)和R(2)。

2.3 组合预测

根据上述组合模型计算得到的预测结果见表3，相对误差波动如图3所示。

由于2017年处于第2种状态，所以考虑矩阵R(1)的第2行中的最大值，确定2018年厦门港集装箱吞吐量仍处于第2种状态，由R(2)确定2019年也处于第2种状态，取第2种状态区间的相对误差的中值，对灰色Verhulst预测值进行修正。根据式(10)得到2018、2019年厦门港集装箱吞吐量马尔科夫修正值分别为1.142 15×107TEU、1.205 66×107TEU。同理可以预测2020—2022年数据如表4所示。

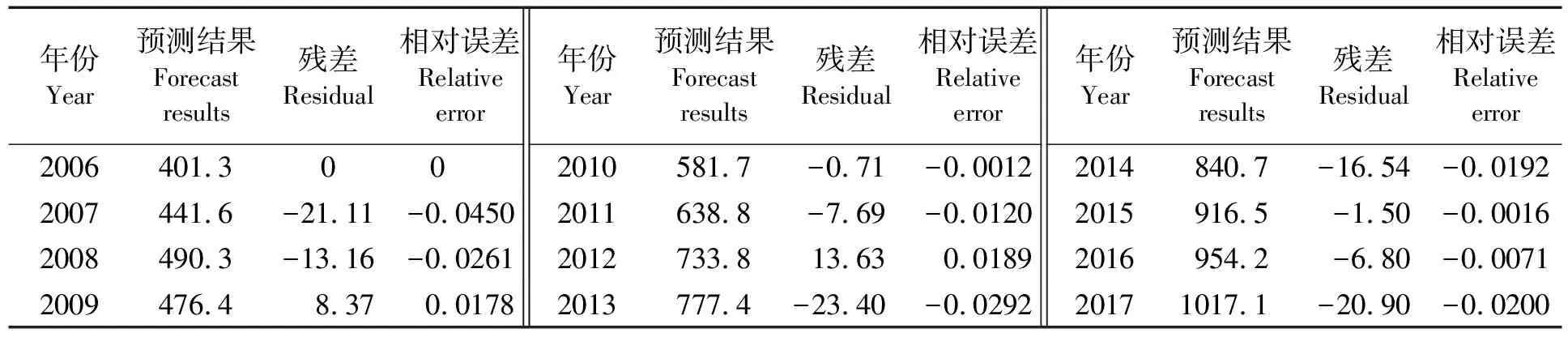
表3 组合预测模型数据

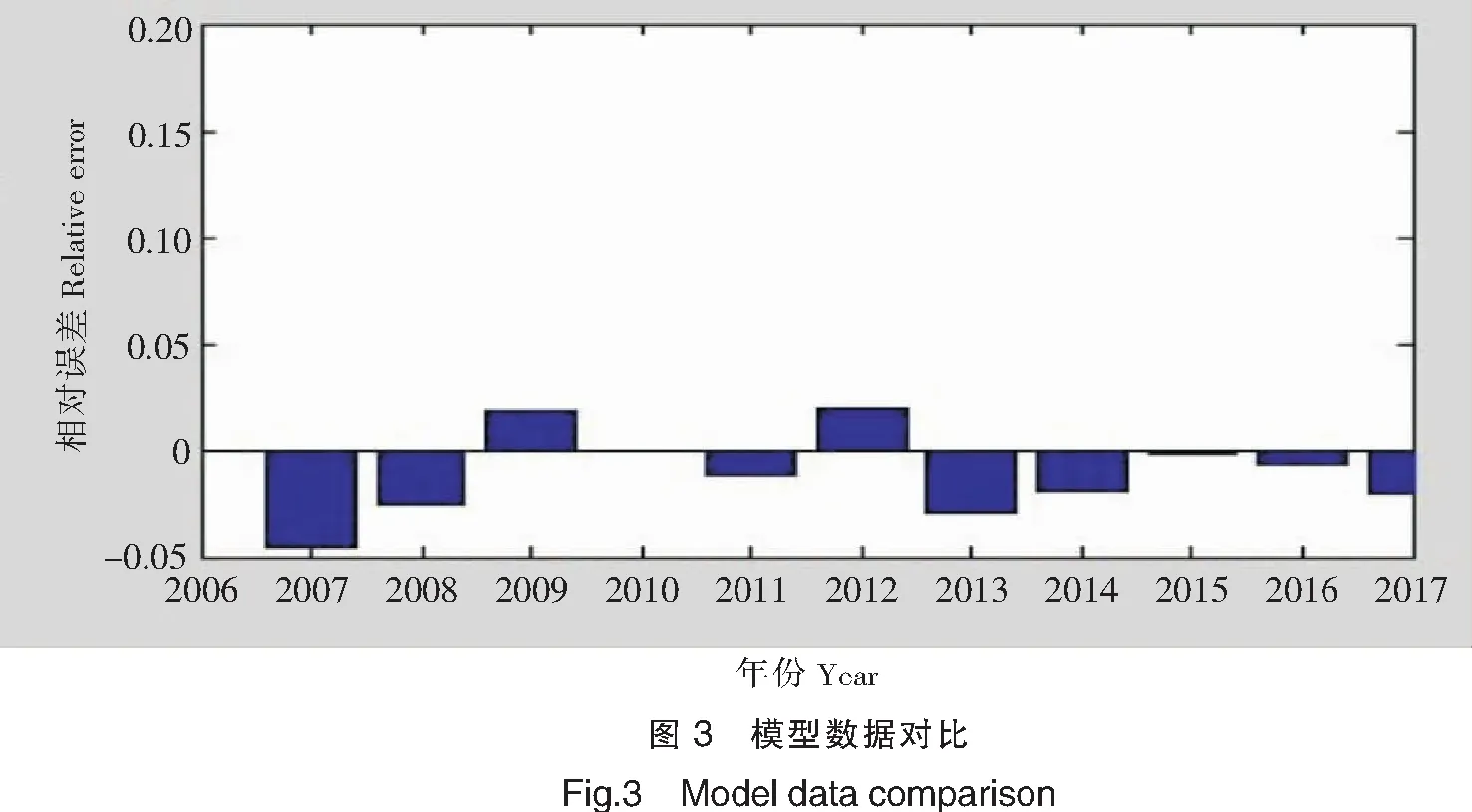
表4 厦门港2018—2022年集装箱吞吐量

年份 Year20182019202020212022集装箱吞吐量Container throughput1142.151205.661266.901325.351380.77

1)平均相对误差

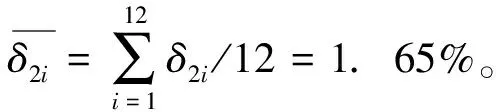
2)模型精度检验

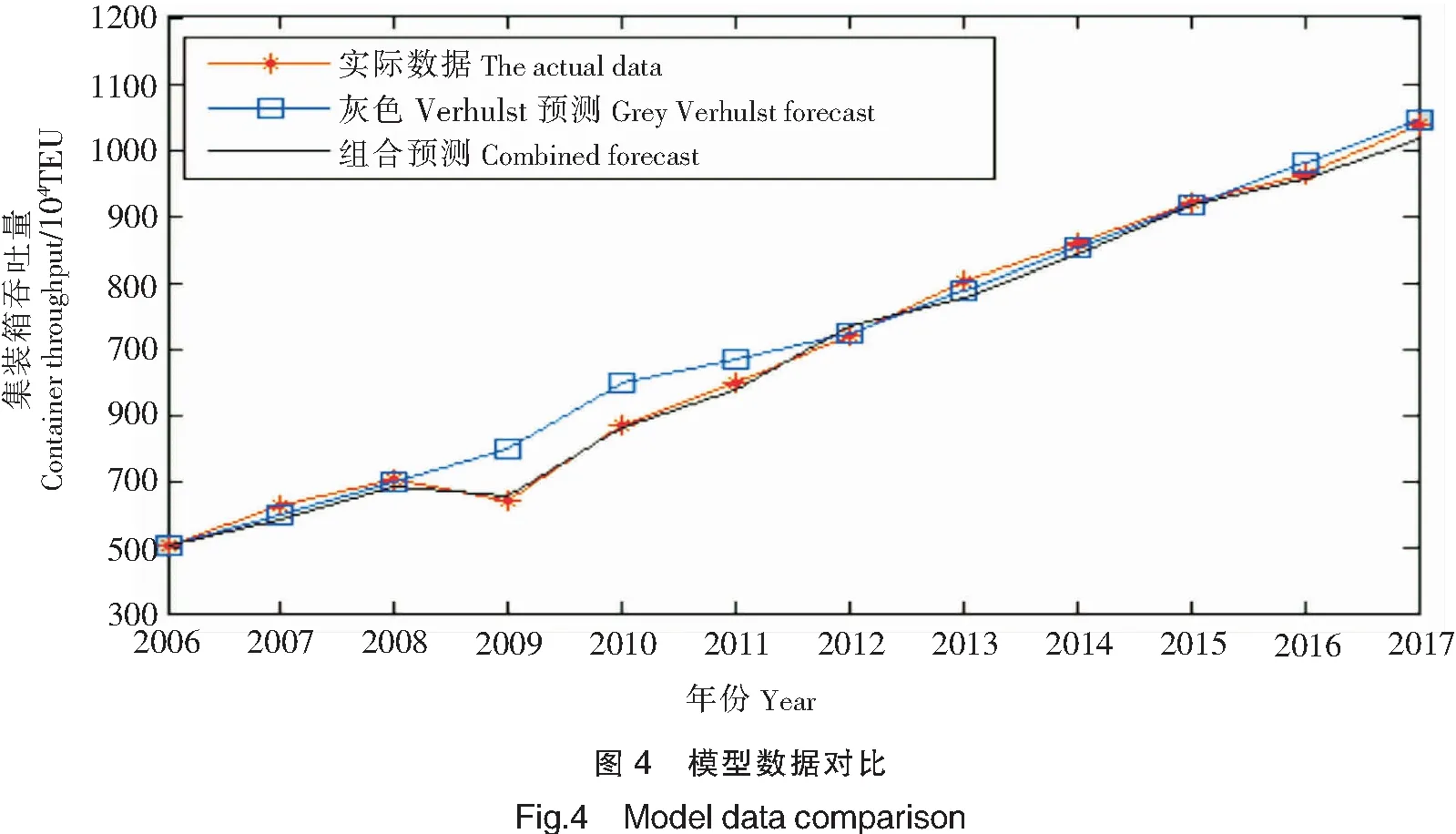
该组合模型平均相对误差为1.65%，低于灰色Verhulst预测的相对误差3.74%，精度达到一级(p≥0.95,c≤0.35)[8]，对厦门港集装箱吞吐量预测数据可信度高。其中各模型拟合情况，如图4所示。

3 结论

本文先利用灰色Verhulst预测模型对厦门港历年集装箱吞吐量进行预测，通过比较发现，预测数据与原始数据之间相对误差波动较大，然后引入马尔科夫模型修正相对误差序列。结果表明预测精度提高了，达到一级水平，进一步可预测未来5年厦门港集装箱吞吐量，希望对厦门港未来建设规划有一定的参考作用。