立足基础 强化联系 突出本质 优化方法
——对“平面向量应用举例”一轮复习课的思考
☉安徽省灵璧第一中学 郑 良
一、问题提出
目前多数学校高三复习采用三轮复习法,一轮复习(时间从9月初到次年3月底)梳理基础知识与基本技能以夯实基础,二轮复习(时间从4月初到5月上旬)突出主干并突破难点以提高技能,三轮复习(时间从5月中旬到高考前)模拟强化,查缺补漏以调适到备考的最佳状态.一轮复习时间长(半年)、内容多(整个高中知识)、任务重(使高中知识与技能系统化、结构化、完整化),是整个高三复习的基础与关键.高三数学一轮复习多以某本教辅为蓝本,按部就班地对知识、技能、方法等逐点扫描和梳理,并适时地补充该教辅遗漏的内容,唤醒学生的记忆.随着时间的推移,学生会对一轮复习照本(教辅材料有详细解答)宣科的教学方式产生疲劳甚至厌倦,学习兴趣持续下降,对一轮复习中学习到的知识与方法愈发模糊.一轮复习结束后学生对知识掌握不牢、理解不透,解题能力不高,应用能力不强,思维踌躇不前.
那么一轮复习课到底该怎么上?近日,笔者在本校听了一节题为“平面向量应用举例”的高三一轮复习课.该班是实验班,生源较好.教师在本节课之前已安排了基础内容“平面向量的概念及其线性运算”“平面向量基本定理及坐标表示”“平面向量的数量积”,同时在授课前一天发放了本节课的学案供学生自主学习探究.下面笔者简录教学过程,给出对相关内容的理解和教学思考.
二、案例评析
例1设且λ+μ=1,则上的投影的取值范围是( ).
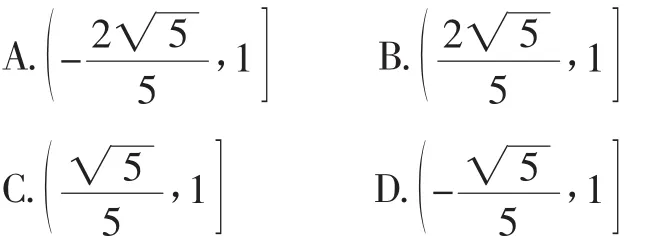
解法1:记上的投影为x,由题意可知
当λ=0时,x=0.
当λ>0时,
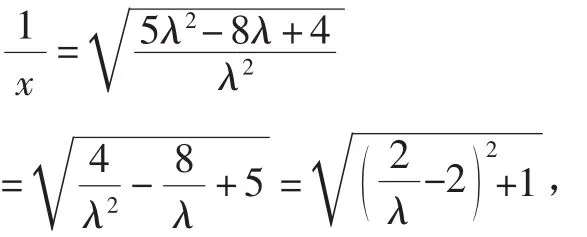
故当λ=1时,取得最小值为1,
当λ<0时,
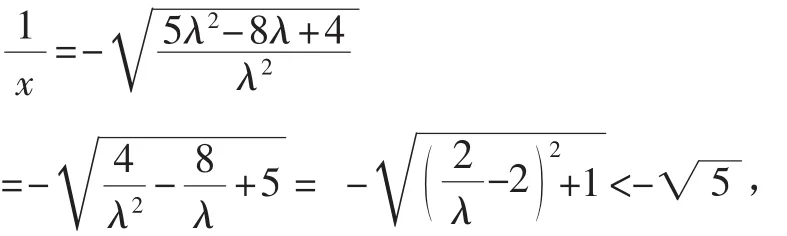
教师展示解法1(多数学生为解析法)后引导学生思考向量基底法与向量坐标法的区别与联系并探寻解法缘由.当学生回答此题为“已知a·b及|a|,求b在a上的投影”类型时,教师追问:“|是已知还是未知?条件中有无与目标相关的不变量(以静制动)?λ+μ=1在此处有无特殊意义(目标指向)?”通过这些问题学生自觉地将两种建系方法(以OA(OB),OB(OA)所在直线分别为x轴,y轴)进行比较以发现哪种方法与条件联系更为紧密.教师在此强调对(向量的投影)概念的理解和对题意的挖掘,并展示部分学生的解法2.
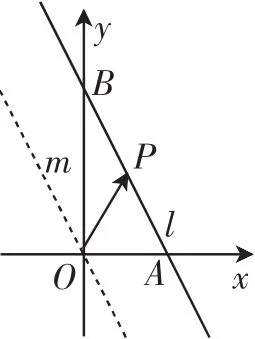
解法2:如图1所示,点P的轨迹为直线l(AB),过点O作直线l的平行线m,记直线l的倾斜角为α,可得.则上的投影为而则有即在上的投影的取值范围是
变式:在中动点G满足若点G的轨迹与直线AB,AC围成的封闭图形的面积为,则BC=( ).

解法1:记△ABC的内角B的对边为b,以A为坐标原点,AC边所在直线为x轴建立平面直角坐标系(图略),则设点G的坐标为(x,y),由,得点G的轨迹Γ的方程为设Γ与直线AB,AC的交点分别为点M,N.由题可知,直线AB的方程为,直线AC的方程为y=0,因此联立(不同的)方程组,得,得b=3,因此在中,由余弦定理可知
解法2:记△ABC的内角B的对边为,由,得,知,所以所以M,G,N三点共线,得点G的轨迹为直线MN,由,得.在△ABC中,由余弦定理可知
教师在投影展示解法1后问学生“你对自己的解法满意吗?”“通过解法1中点M,N的位置及刚刚学习的例1,你有哪些新的想法?”之后教师展示(少数学生在教师提示前已独立思考得到)解法2,并与学生一起回顾数乘向量的定义及实数的常见变换并强调向量中的三点共线定理是必修4教材第84页的例3(投影展示).
点评:教师正本清源,回归教材,关注概念,注重过程,适度整合,让学生在自然中深化知识(向量的投影、向量中的三点共线定理等),领悟数学思想(数形结合、化归与转化等).教师没被少数资优生拉快教学进度,而是基于学情,乐于等待,善于启发,引领学生透过现象看本质,培养学生良好的学习习惯和理性思考的精神,对少数的资优生与后进生进行单独交流、个别指导.解题倡导“就近上车”,教师就要让学生看到车且能登上车.如例1解法2体现了极限思想,先展示公式法后展示定义法,变式中先呈现解析法再呈现公式法,使学生拾级而上,认识从浅显到深刻,思维从低阶到高阶.
例2已知△ABC是边长为2的等边三角形,点P为平面ABC内一点,则的最小值是( ).

解法1:以线段BC的中点D为坐标原点,BC所在直线为x轴建立平面直角坐标系,则C(1,0),设P(x,y),下略.
解法2:记BC的中点为点D,则,当且仅当点P为DA的中点时等号成立.
解法1为通性通法,(部分学生发现)A,B,C位置相对固定,可直接利用向量的极化公式(a-b)2]来求解.教师指出本题为2017年全国卷Ⅱ理科第12题,解法1为解析法,解法2为几何法,还有均值不等式法等,并提醒学生仔细审题,力求“多想少算”,用深刻的思维代替熟练的操作.
变式:已知不共线的两个向量a,b满足|a-b|=2,且a⊥(a-2b),则|b|=( ).

解法1:由a⊥(a-2b),得a·(a-2b)=a2-2ab=0,由|ab|=2,得a2-2ab+b2=4,从而得b2=4,即|b|=2.
解法2:作a-2b,如图2所示,由a⊥(a-2b)知∠AOC为直角,取AC的中点为D,则,由直角三角形斜边中线的性质知,因此有

图2
解法3:由a⊥(a-2b),得,从而有|b|=|a-b|=2.
教师呈现解法1后追问结论(|b|=|a-b|)“是巧合还是必然?”“你还能从不同的角度给出解释吗?”向量是沟通几何与代数的桥梁,学生重新审视条件,给出解法2与解法3.解法2给出了向量垂直的不同表征,解法3根据目标对条件实施恒等变形,而2a=(a+b)+(a-b),2b=(a+b)-(a-b)等变形在实数变换中司空见惯,通过类比迁移来强化联系.
点评:教师强化恒等变形,例2中解法2本质为消元法构建目标函数,比代数法更加清楚直观.教师通过例题展现出高考题是如何实现对学生思维能力的考查,揭开了高考题神秘的面纱,减缓甚至消除了学生对高考题的陌生感与恐惧感.教学不能止于正确结论的获得,更应该提倡学生学会独立思考、自主学习、合作交流等多种学习方式,激发学生学习数学的兴趣,培养学生养成良好的学习习惯,从而促进创新意识的发展.变式相对基础,平凡而不平淡,教师引导学生发散思维、深入反思,充分发挥“小问题,大道理”的作用,使学生的观察力以及思维品质在潜移默化中进阶、优化、提升,同时获得精神上的愉悦.
例3已知,|b|=3,a与b夹角为45°,求使a+λb与λa+b夹角为锐角的实数λ的取值范围.
解法1:由已知得
解法2:(a+λb)(λa+b)=3λ2+11λ+3.由a+λb与λa+b夹角为锐角,得3λ2+11λ+3>0,则而当a+λb与λa+b同向时,存在正实数μ>0满足a+λb=u(λa+b),有得λ=1或λ=-1(舍).所以实数λ的取值范围为
几乎每个学生都采用解法2来解题,教师让学生分析解法1与解法2,明晰问题的逻辑,体会解法2的割补法和化归与转化思想,强调化归与转化过程中的等价性.
变式:设向量a、b、c满足c〉=60°,则|c|的最大值等于( ).

图3
又因为〈a-c,b-c〉=60°,所以O,A,C,B四点共圆.所以当OC为圆的直径时,|c|最大,此时∠OAC=∠OBC=90°,则∠ACO=∠BCO=30°,所以可 得
教师结合选项从最大值(边界的函数值)概念的角度肯定了答案的正确性.要求学生反思求解过程,此时有少数学生(抢答)意识到图形的对称性,教师引导学生从代数角度确定c的“终点”位置,学生以点O为坐标原点,OA所在直线为x轴建系求解无疾而终.又尝试根据OA与OB的对称性建系简化运算,得到如下解法2.
解法2:设则,则∠AOB=120°.以O为坐标原点,∠AOB角平分线为x轴建系,如图4所示,则设,则由°,得
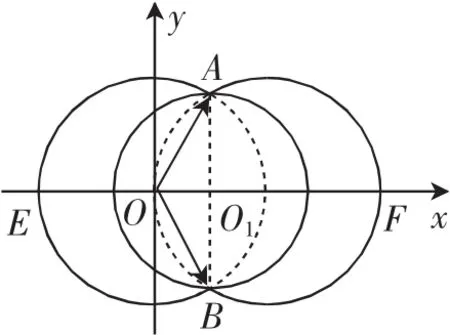
图4
平方整理得

则有(x-1)2+y2=1或x2+y2=1(且满足≥0),即点C的轨迹为(以(1,0)为圆心,1为半径的)和(以(0,0)为圆心,1为半径的)故当点C与点F重合时,|c|最大,最大值为2.
教师指出解法1只考虑了凸四边形而遗漏了凹四边形的情况,强调数形转化的等价性,谨防形的误导.教师组织学生再次对题目条件进行推敲,发现问题的本质是“已知,求点C的轨迹”的解三角形问题.
点评:用非零向量a与b的数量积来刻画a与b的夹角要用到向量a与b的模,过程繁琐,而a·b>0等价于〈a,b〉其中a与b共线易于判定,利用“多退少补”等价转化.例3解法2的本质是先利用结论的必要条件再验证其充分性.多数学生解题推理不够严密,书写不够规范,变式解法1实质是用充分条件代替充要条件,因为该充分条件包含“最大值点”,出现了逻辑错误而答案正确的情形,解法2不仅为问题提供了几何背景,更为学生的学习敲响了警钟,也对命题人提出了更高的要求.
三、教学思考
高三数学一轮复习需要对学过的基础知识进行归纳整理,同时还要对某些内容重点突破、深度挖掘,实现各部分内容之间的衔接与整合,促进知识的融会贯通与思想方法的相互渗透,提升学生的数学能力和综合素养.
1.解读纲领文件 深入研究教材
高考考什么?怎么考?教师要了如指掌,学生要心中有数.以理科为例,基于高考命题的稳定性,教师应反复研读《普通高中数学课程标准(2017年版)》,深入解读上一年的《普通高等学校招生全国统一考试大纲(理科)》、《普通高等学校招生全国统一考试大纲的说明(理科)》,精准领悟近几年的《高考理科试题分析(语文、数学、英语分册)》,待新文件颁布后只需微调即可.教师要弄清目标导向,反复研习教材,如在授课中,受限于(期中、期末等)统考进度和学生认知水平等原因,教师对部分内容只能采用抓大(主干重点)放小(精致内涵)且混而不错的方式教学,复习时则需要对此查缺补漏,正本清源,打好基础,切实弄透教材中的每一个概念、公式、法则、性质、公理、定理,充分发挥教材中例题、习题的功能,通过变式推广,学生由浅入深,潜移默化地加深对问题的理解.如“充要条件”内容安排在选修教材2-1中,必修4新授课时只能用描述性语言讲解例3,复习课时则应和盘托出,又如例1中对向量的投影概念的理解,其变式利用数乘向量对条件标准化(向量的三点共线定理)等根植教材,只有深入研究教材才能最大限度地发挥教材的育人功能.
2.构建知识体系 强化推陈出新
人的认知结构是动态的、开放的.教学时应掌握课程的整体结构,分析教材的知识结构及前后的逻辑关系,引导学生厘清新授课中孤立的、不连续的知识之间的关系,发现知识的本质,让学生搭建起稳定而有序的知识结构.当学生的认知结构产生冲突时,就会对原有的认知结构产生质疑、思辨、整合,重新构建更加兼容稳固的认知结构.一轮复习与二轮复习绝不是时间上的区别,而是立足于学情的统筹安排.复习时要避免说教,要用新颖的情境、出乎意外而又情理之中的方式(内容理解、解法呈现等)提升学生的数学素养,引领学生会用数学眼光观察世界,会用数学思维思考世界,会用数学语言表达世界.教师要提供足够的时间与空间让学生尝试多方切入,提高学生的思辨能力、整合意识和创新意识.如例2的解答不能止于解法1,要引导学生发现解法2.例2的变式通过特殊与一般的思考,借助数形结合思想,使解法2与解法3给人以美的感受.
3.聚焦数学本质 积累活动经验
现象千变万化,本质始终如一.数学学习要分清问题的源与流,透过现象看本质.只有抓住问题的本质,才不会被现象所蒙蔽,才能切实感受到数学的力量.数学本质的发现不是一蹴而就的,过程曲折甚至非常艰难,这就需要学生具备扎实的基础知识、沉着冷静的思考方式以及锲而不舍的探究精神等.通过对问题本质的探寻过程,发展学生思维,积累活动经验,体会人生智慧.本节课所选内容简单平实,教学处理层次分明,问题本质逐步凸显,学生经验不断提升.H

