初速可控舰炮对海上目标命中概率的影响

吴 威，吴 玲，卢发兴

（海军工程大学电子工程学院，武汉 430033）

0 引言

传统舰炮发射弹丸初速固定，随着新能源发射技术的快速发展，电磁轨道炮、电热化学炮等新能源武器发射的弹丸初速可调，应用前景广泛［1-2］。但初速可调将影响弹丸对目标命中概率，改变传统舰炮对目标的打击方式。不同于传统舰炮，弹丸初速可调，则对同一目标进行打击时采用不同的弹丸初速和弹丸射角，弹丸飞行时间、弹丸落角和弹丸落速将改变，弹丸对目标的命中概率随之改变。因此，存在最佳弹丸初速，实现对目标的最大命中概率。

关于弹丸初速对目标命中概率的影响，目前国内只对舰炮初速对命中点预测误差影响有所研究分析［3-4］。本文通过建立海上目标运动模型，利用Cramer-Rao下界理论推导得到目标运动要素估计误差精度，根据弹丸外弹道方程和弹丸对海上目标的命中概率模型，分析弹丸初速对目标命中概率的影响，为新能源武器火控解算、最佳初速射表制定提供理论依据。

1 海上目标运动模型

对于海上舰船等慢速目标，在舰炮火控计算中，通常把通过雷达测得目标的球坐标值转换为直角坐标系两个坐标轴上的观测值［5］，以便于求解目标运动参数和解命中，对目标实施打击。在火控系统计算中，在误差允许的范围内，将直角坐标系中的相关观测噪声转换为不相关高斯白噪声，可以提高系统的反应时间［6］。为了简化计算，把目标运动分解为单个坐标轴上的单独运算，而不考虑两个坐标轴误差分量之间的相关性，造成的精度误差在10%以内［7］。这样，可以将对一个目标的跟踪问题转化为根据两个坐标轴上的2k个测量值、估计目标运动要素、的问题。

以目标在X轴方向进行匀速直线运动为例，得到其运动方程：

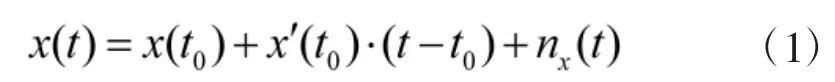
式（1）的观测方程为

式中，

其中，N（x）为观测噪声，dt为数据采样间隔。

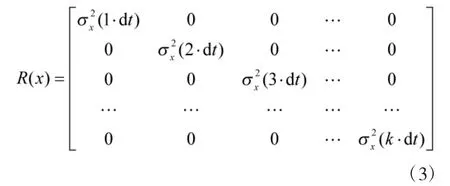
2 目标运动要素估计误差的CRLB

为了分析对海射击误差，需要根据目标运动模型确定目标运动要素估计误差的精度下限，即CRLB（Cramer-Rao Lower Bound）［8］。

设到k时刻止，获得的测量集为X={Xi|i=1，2，…，k}，则它对目标运动要素H（x）估计的似然函数为

因此，

对于测量集X的H（x）的似然函数为

所以

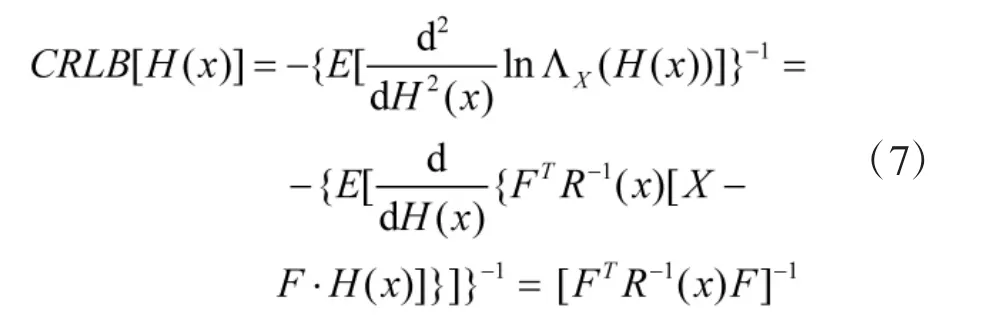
可以得到对目标运动要素H（x）估计误差的Cramer-Rao下界。设滤波时间为T，预测时间参数为η，预测时间为ηT，则预测目标在T+η·T时刻的X轴位置误差的Cramer-Rao下界为

把式（2）和式（3）代入式（7）可得

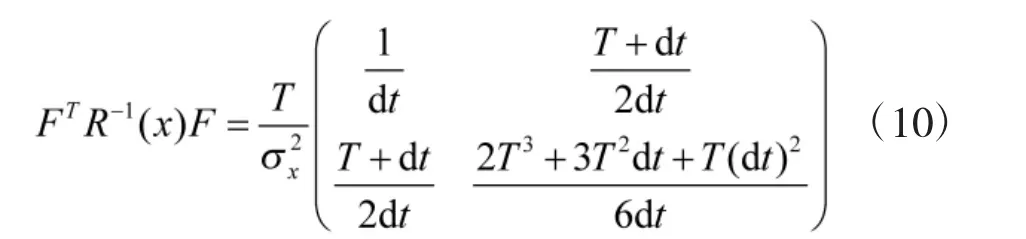
由式（10）可得

代入式（8）可得预测目标为匀速直线运动时，在T+η·T时刻的X轴预测位置误差：

同理，可以预测目标为匀速直线运动时，在T+η·T时刻的Y轴预测位置误差：

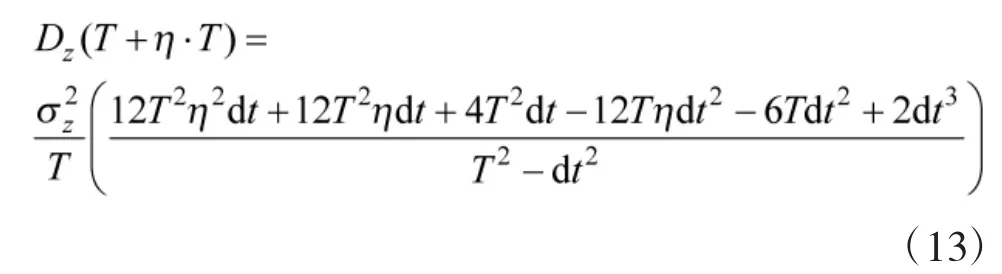
3 弹丸外弹道模型

为了分析初速对命中概率的影响，还需要获得弹丸落角、落速和弹丸飞行时间，为此建立弹丸外弹道模型［9］。采用直角坐标系OXYZ，O在发射点，轴线OX位于水平面上，方向为弹丸移动方向；轴线OY垂直于轴线OX，方向为垂直向上；轴线OZ垂直于轴线OX和OY，建立右坐标系。考虑弹丸旋转、科里奥利力、重力加速度以及偏流的影响，可以得到弹丸运动微分方程组为：

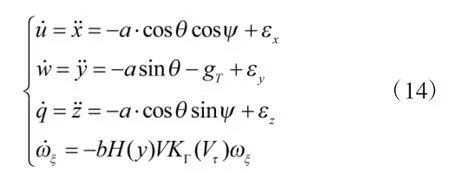
其中，（x，y，z）为弹丸矢径，（u，w，q）为弹丸速度矢量，ωξ为弹丸纵轴方向的角速度，为空气阻力加速度，ψ为偏流角，θ为弹丸倾角，V为弹丸速度，H（y）为空气密度函数，K（Γ）为极阻尼力矩函数，转动系数b为常数，εx，εy，εz为各个方向的修正加速度，其数学表达式为：

其中，（x，y，z）为弹丸矢径，（u，w，q）为弹丸速度矢量，gT（φ，y）为弹丸高度为时的重力加速度，f（t）为偏流系数，R（y）为曲率半径，Ωx，Ωy，Ωz为地球自转角速度 Ω 在 x，y，z轴上的分量，Ω=7.292 1·10-5rad/s。

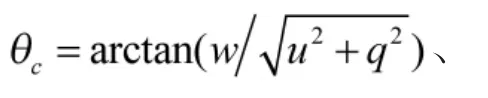
4 弹丸对海上目标命中概率模型

4.1 海上目标命中面积

海上目标命中面积是弹丸可击中的目标面积，一般可根据等面积替代原则，用规则形状的目标面积近似代替舰艇命中面积［10］。以水面舰艇为例，设目标舰艇甲板面等效矩形长为Lf，宽为Bj，如图1（a）中的ABCD所示，舰艇平均舷高为Hp。

图1 舰艇命中界示意图

考虑到目标舷角Qm，则计算目标命中面积时，需要把矩形ABCD沿弹丸射向方向进行投影，如图1（a）所示。同样根据面积等效原则，得到投影后的矩形 A'B'C'D'边长 C'D'=Lz，B'C'=B'j，有

再考虑舰艇舷高Hp沿弹丸落速方向的投影，则舰艇水平投影面积变为A2=Lz·Lx，如图1（b）所示，则

其中，θc为弹丸落角，即弹丸击中目标时，弹丸速度方向与水平面的夹角。式（18）将命中面积均投影在水平面内，一般情况下可简化Lx的计算，但当弹丸落角 θc极小时，利用式（18）计算 Lx将无限大，与实际不符。因此，将舰艇命中面积投影在弹丸落速的垂直面上，记为Aj，即图1（b）中阴影矩形MNPQ面积：

4.2 舰炮对海射击误差

舰炮武器系统对海射击误差包含随机误差和系统误差。随机误差主要考虑舰炮射弹散布误差和随动系统误差的合成［10］，一般情况下，随机误差可通过下式进行计算：

其中，kEx和kEz分别为距离和方向误差系数，d为射击距离。

舰炮对海射击的系统误差一般可认为主要由火控系统误差中的目标定位误差决定，因此，系统误差mx、mz可取为目标运动要素估计误差的精度下限CRLB与一定系数的乘积，由式（12）、式（13）可知：，其中，kmx、kmz为系统误差系数，kmx>1，kmz>1，ρ=0.476 9 为正态常数。

4.3 命中概率模型

假设以目标中心为瞄准点时目标命中界为Lx'×Lz。考虑对海上目标射击时，目标在x轴和z轴上的随机误差分量相互独立，则发射一发弹丸对此矩形目标的命中概率 P（x，z）为：

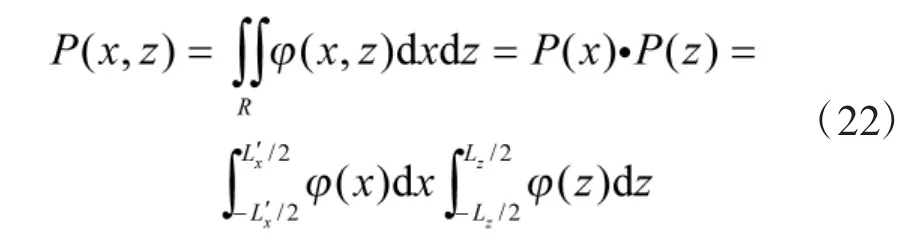
其中，φ（x）、φ（z）分别为弹着散布误差在 x、z轴上的正态分布密度函数，即：

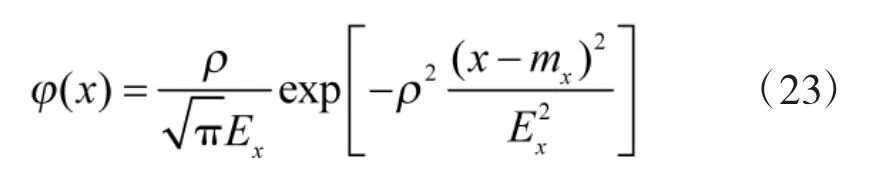
类似可得 φ（z）。

5 算例分析

5.1 海上目标命中概率计算框架

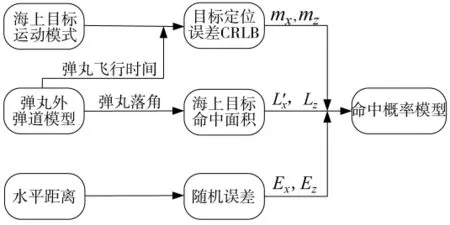
图2 海上目标命中概率求解流程图

1）如图2所示，首先建立海上目标运动模型，根据弹丸飞行时间（预测时间）以及滤波时间，求解目标定位误差精度下限 CRLB，并由式（12）、式（13）得到射击系统误差 mx，mz；

2）根据射击距离，由式（21）得到射击的随机误差 Ex，Ez；

3）根据弹丸外弹道模型计算弹丸落角，并由式（16）、式（20）计算海上目标命中界 Lx'，Lz；

4）由海上目标命中概率模型式（22），可得命中概率。

5.2 算例分析

对于初速可控的舰炮，对目标进行打击时，可根据目标的远近，选择不同的弹丸初速以及弹丸射角。首先分析射击误差对命中概率的影响，然后分析不同初速情况下目标距离和弹丸射角对命中概率的影响；最后重点分析打击视距内目标时，弹丸初速与命中概率的之间的关系。

假设某目标驱逐舰甲板面等效长度Lj=124 m，宽度Bj=20.5 m，舷高Hp=10.33 m，目标舷角Qm=π/2，航速20节，航向与我舰航向相反。由式（16）、式（20）可得 Lx'，Lz，取滤波时间 T=4 s，数据采样间隔dt=0.01 s，σx=30 m，σz=20 m，kEx=1/300 rad，kEz=1 ×103rad，kmx=kmz=2。

5.2.1 射击误差对命中概率的影响

对18 km目标进行打击，分析射击随机误差和系统误差对目标命中概率的影响。表1给出了系统误差随弹丸初速的变化情况，下页图3给出不同随机误差情况下弹丸初速对弹丸命中概率的影响，图4给出了不同系统误差情况下弹丸初速对弹丸命中概率的影响。

表1 系统误差随弹丸初速变化情况表

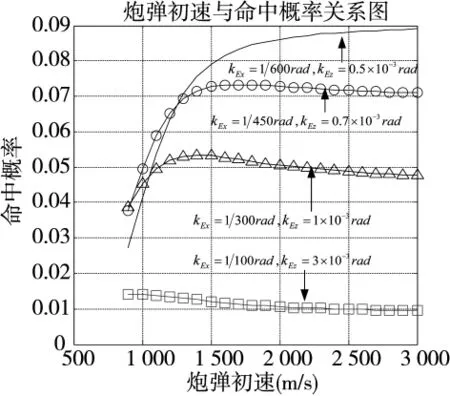
图3 不同随机误差情况下弹丸命中概率随弹丸初速变化图

图4 不同系统误差情况下弹丸命中概率随弹丸初速变化图

由表1及图3、图4可知：当舰炮射击随机误差远大于系统误差时，命中概率随舰炮初速的增加而减小；当随机误差远小于系统误差时，命中概率随初速增加而增大；当两种误差取值相当时，命中概率随初速增加先增加后减小。上述结果的出现是由于初速增大，弹丸飞行时间减少，射击系统误差减小，将使命中概率有增大的趋势；而同时初速增大时，落角减小，造成目标命中界变小，又使命中概率有减小的趋势。当两类射击误差取值比重不同时，系统误差和命中界变化对命中概率的影响比重也不同。

因此，在进行初速可控舰炮武器系统设计时，要充分考虑其对舰炮随机误差与系统误差的精度匹配，以达到对目标最大的命中概率。后续计算均针对射击的随机误差和系统误差取值相当的情况，分析初速对命中概率的影响，即随机误差系数取值为kEx=1/300 rad，kEz=1×103rad，系统误差系数取值为kmx=kmz=2。

5.2.2 目标距离对命中概率的影响

分别以 1 500 m/s、2 000 m/s、2 500 m/s 弹丸初速对不同距离目标进行打击，图5给出了不同弹丸初速条件下目标距离与命中概率关系图。

由图5可知，在不同弹丸初速条件下，弹丸对目标的命中概率均随着目标距离的增加而降低，当目标距离超过视距界限时，弹丸对目标的命中概率渐趋平稳，且均处于较低值。可见，对超视距远目标进行打击，在传统弹丸不能获得较好效果时，应采用新型信息化制导弹丸，以提高弹丸射程和命中概率，此时命中概率主要由信息化制导弹药的制导能力决定。因此，本文重点研究对视距内目标打击时弹丸初速和射角对命中概率的影响。

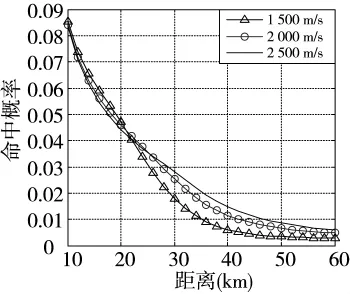
图5 弹丸命中概率随目标距离变化图

5.2.3 弹丸射角对命中概率的影响

分别以1 000 m/s、1 500 m/s弹丸初速对视距内18 km目标进行打击，每种初速均采用高低两种射角发射，弹丸外弹道示意图如图6所示。计算得到的视距内弹丸的高低弹道飞行参数和对目标命中概率如表2所示。

图6 弹丸外弹道示意图

表2 弹丸飞行参数及命中概率

由图6和表2可以看出，对视距内目标实施打击，当弹丸初速相同，弹丸有小射角低抛弹道和大射角高抛弹道两种射击方式，采用小射角低抛弹道射击时，弹丸飞行时间短，命中概率高，因此，对于视距内目标打击应采用低抛弹道，命中概率高，同时可以大大减少目标的预警反应时间，提高命中效果。

5.2.4 视距内弹丸初速对命中概率的影响

对这一部分进行重点分析。假设目标舰艇距离18 km，由式（12）～ 式（23），对命中概率随弹丸初速变化情况进行计算，结果如表3和图7所示。表3给出了不同初速条件下，弹丸飞行参数以及弹丸对目标的命中概率；图7给出了目标命中概率随弹丸初速、目标距离变化情况。

表3 弹丸命中概率随弹丸初速变化表

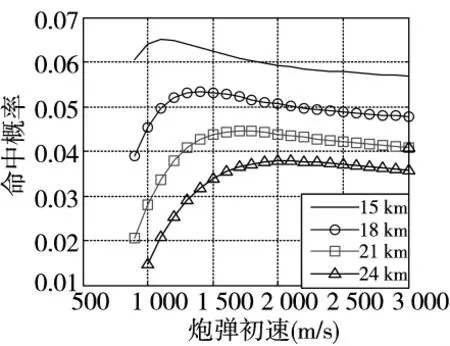
图7 命中概率随弹丸初速变化图

由计算结果表3和图7可知，在打击视距内目标时：

1）对不同距离的目标，随着初速可控舰炮弹丸初速的增加，弹丸飞行时间、弹丸落角逐渐降低，弹丸落速逐渐增加，弹丸对目标的命中概率先增加后降低。因此，存在最佳弹丸初速，使得弹丸对目标的命中概率最大。

2）目标距离越远，增加弹丸初速，命中概率提高越显著，达到最大命中概率对应的最佳弹丸初速越大；

3）使用相同初速的弹丸对不同距离的目标进行打击，目标距离越远，命中概率越低。

综上可知，初速可控舰炮的弹丸初速对目标命中概率有很大的影响。打击视距内目标时，可将弹丸加速至最佳初速，实现对目标的最大命中概率。且由于新能源武器弹丸初速与消耗能量成正比，通过调整弹丸初速，不仅可以实现弹丸的最大命中概率，还可以优化每次发射弹丸的能量，提高发射率。

此外，本文选取目标速度5 kn～50 kn，仿真分析了目标速度差异对舰炮命中概率的影响。结果显示，弹丸初速固定时，对不同速度的目标实施打击，命中概率变化不大。因此，在本文中对这一部分不展开详细分析。

6 结论

基于海上目标运动模型、弹丸外弹道模型和目标运动要素估计误差模型，建立了弹丸对海上目标的命中概率模型，计算分析了弹丸初速对目标命中概率的影响。可以得到：与传统舰炮射表不同，弹丸初速可控的新能源武器应建立外弹道最佳弹丸初速射表，这对于火控解算等实际工程应用具有重要意义。