先验有色噪声补偿的卡尔曼滤波组合导航算法

杨 其 ，刘新学 ，孟少飞 ，刘庆宝

（1.火箭军工程大学初级指挥学院，西安 710025；2.火箭军工程大学士官学院，山东 青州 262500）

0 引言

飞行器在实际使用工况下，由于受到发动机振动、气流扰动等因素的作用，始终处于复杂动态环境中，会造成与之相固连的捷联惯导误差模型系数发生改变，产生随机动态误差。虽然目前各种研究和试验均而表明动态条件下的随机误差与静态标定环境下并不吻合［1-2］，但目前大多数飞行器误差模型仍将其归入单纯的随机误差，并未进行来源和成因的分析，也没有相应标定的方法，一方面原因是因为动态环境的复杂性无法精准预测，另一方面原因在于振动对惯导设备带来的影响缺乏根源性的机理分析。目前对于随机误差的研究多集中在导航算法研究上［3-5］，利用卡尔曼滤波方法对误差进行滤波补偿可以有效克服惯导系统静态误差模型的局限，提高导航解算的精度。但卡尔曼滤波在驱动参数设置不科学的前提下，也会存在收敛较慢甚至发散的可能。本文从惯导安装的动力学模型出发，利用模态分析的方法求解动态误差的数字特征，设计考虑有色噪声补偿的增强卡尔曼滤波，并利用算例仿真验证了方法的可行性。

1 惯导本体动态响应分析

在忽略惯导本体内部受力变形和仪表级随机安装误差等因素时，即假设本体具有绝对刚度情况下，根据实际工况假设受到弯扭耦合激励的扰动，将惯导安装支架等效为Timoshenko梁，减振系统等效为弹簧（横向振动）、扭簧（扭转振动）和阻尼器，惯导本体等效为质量件，系统受到沿Timoshenko梁横向作用力 p（x，t）和绕剪切中心的扭转力 q（x，t）的共同作用，且认为梁的剪切中心和截面质心并不重合，两者之间距离为χα，等效混合系统如图1所示。

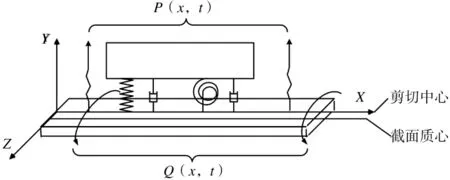
图1 等效混合系统示意图

Timoshenko梁是基于初等力学中平截面变形假设的梁模型，即假设初始垂直于中性轴的截平面在变形时仍保持垂直，但考虑剪切变形和转动惯量。借鉴文献［6-7］中利用哈密顿原理建立的Timoshenko梁运动方程，可得混合系统运动微分方程为：

式中，上标（·）表示对时间求导；上标（'）表示对位置求导；c1、c2、c3分别表示梁的弯曲振动阻尼、截面旋转阻尼、扭转振动阻尼；EI表示梁的弯曲刚度；kGA表示梁的截面旋转刚度；GJ表示梁的剪切刚度；θ表示横向振动引起的梁截面旋转角度；w表示梁的横向振动位移；ψ表示梁的扭转振动角度；ρI表示梁的转动惯量；m表示梁的线密度；Iα表示单位长度梁的惯性矩；mi表示振子质量；wi表示振子横向振动位移；civ表示振子横向振动阻尼器的阻尼系数；kiv表示线弹簧刚度系数；xiv表示线弹簧安装位置；Ji表示振子转动惯量；ψi表示振子扭转角度；cir表示振子扭转振动阻尼器的阻尼系数；kir表示扭簧刚度系数；xir表示扭簧安装位置；δ（）表示 Dirac函数；Fiv、Fir分别表示横向振动和扭转运动约束力。

通过观察等效系统可以发现，弹簧振子与梁仅在弹簧安装位置发生相互作用，在方程形式上等效于梁上一点激振力引起的动力学响应，即梁结构振动的Green函数形式［8-10］。利用弯扭耦合情况下的格林函数求解并对系统进行复模态分析，在假设系统阻尼为非经典情况下，最终可求得振子横向振动中响应位移、响应加速度协方差函数为：

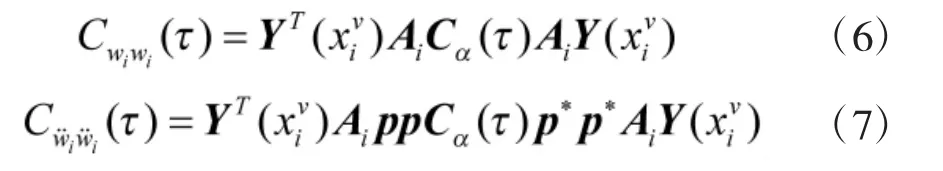
式中，αn（t）表示系统的模态响应，p为特征值矩阵，Ai表示梁位移与振子位移关系的矩阵，Y表示分离变量系数矩阵，表示αn（t）的协方差函数矩阵。

同样获得振子扭转响应角度协方差函数为

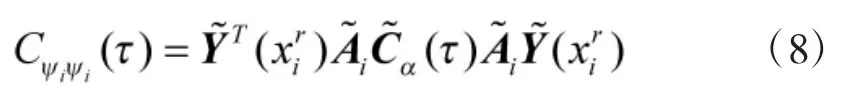
2 先验有色噪声的确定

通过混合模型响应分析，可以看到惯导本体在受到外部激励后，会围绕静态安装位置产生微小的横向振动和扭转振动响应，而响应产生的加速度和角速度也被惯性仪表所敏感进入导航解算，直接产生测量误差，即

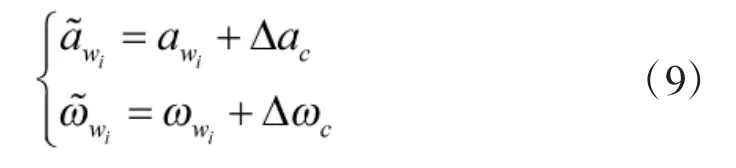
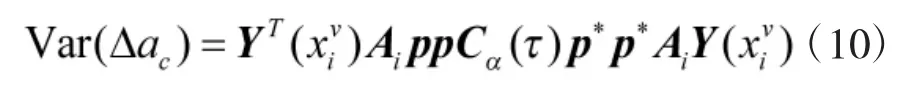
另一方面，当本体质心与飞行器质心不重合，存在安装杆臂时，当飞行器持续受到外部激励时捷联惯导本体也将持续产生动态响应［11］，即本体质心P始终处于变化中，杆臂rp也不再为常量，则杆臂变化造成的加速度误差应表示为：

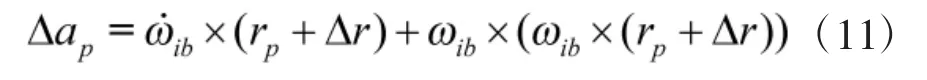
式中，ωib为飞行器角速度，Δr为杆臂变化量。

不失一般性地认为杆臂误差仍围绕静态条件下常值发生变化，根据式（6）并结合方差性质，可得杆臂变化量的方差为

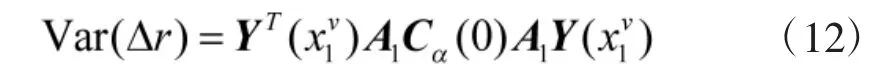
在动态响应条件下外杆臂矢量变化造成加速度误差的方差为：

式中，C1、C2代表由位置关系决定的常系数。而同时发生的绕扭转振动轴的旋转运动虽然不会造成杆臂矢量的变化，但旋转会造成加速度计敏感轴方向发生变化，如图2所示。

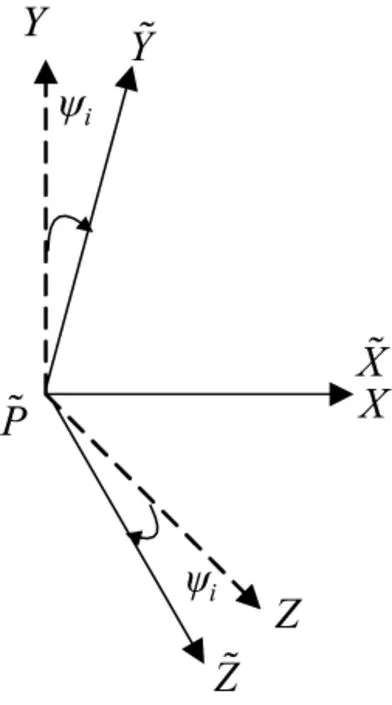
图2 绕X轴旋转

式中，Cbt表示由本体坐标系向地理坐标系的转换矩阵，ab表示本体坐标系中敏感到的加速度，at表示转换到地理坐标系后的加速度。

而在扭转响应的情况下，真实本体坐标系中敏感到的加速度转换到地理坐标系中应表示为：

由此造成的加速度转换误差可表示为：

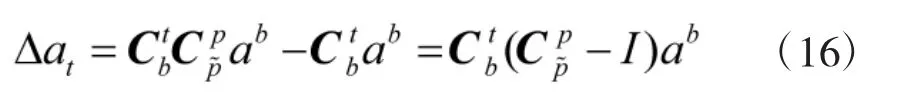
结合式（8）可以求得该误差的方差Var（Δat）。

显然，在动态条件下惯导本体受激响应导致的误差在误差模型中被归入随机误差，加速度产生的随机误差Δa主要由Δac、Δap和Δat组成。为了使机理更为清晰，本文仅分析了受激响应对加速度造成的影响，按照同样的方法考虑扭转振动并结合几何位置关系，可以得到受激响应对角速度影响，即陀螺的随机误差，文中不再赘述。

3 有色噪声补偿的卡尔曼滤波

在未获得先验有色噪声信息的情况下，组合导航卡尔曼滤波在使用中对于惯性仪表的随机误差一般以白噪声来描述，以Ψ角误差方差为基础推导而来的惯导系统方程可描述为［10］：

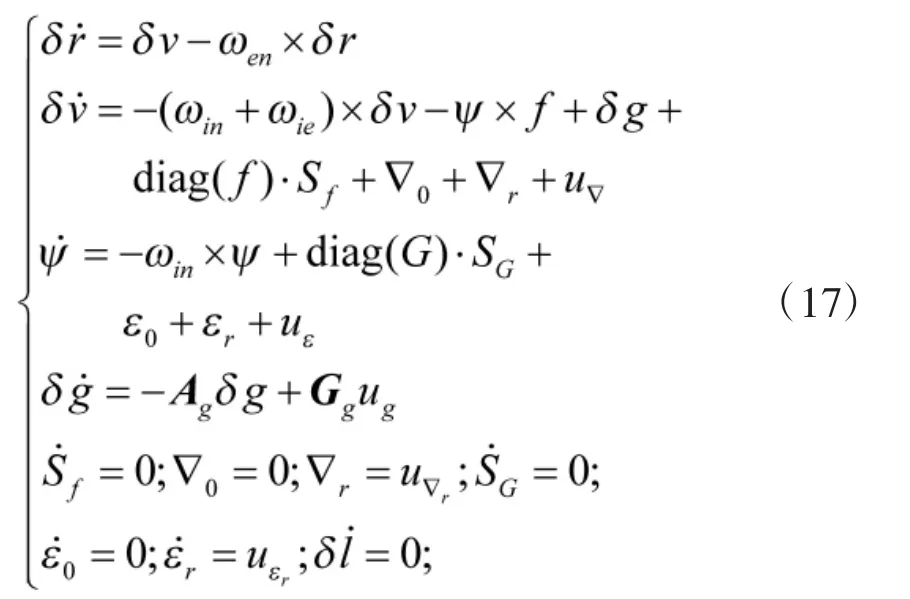
式中，x为状态变量，F为系统矩阵，可由式（17）求得，u为系统噪声，即

根据文献［4］，上述系统为线性时变系统，各状态均可观测。

以白噪声作为随机误差，其意义主要在于可以直接作为卡尔曼滤波的系统驱动噪声，但通过前文分析可以看到在等效Timoshenko梁混合系统情况下，惯性仪表的部分随机误差应属于有色噪声，应对其进行微分方程描述并导入到惯导系统误差模型中［13-14］。借鉴文献［15］系统可描述为：

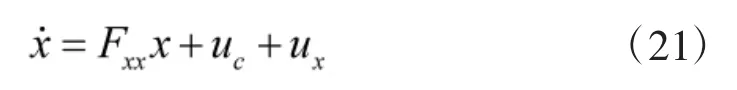
式中，uc为有色噪声，ux为等效白噪声。

以3个轴向上加速度计和陀螺的有色噪声组成的状态空间zi，构造能观标准型并结合uc的状态空间推导，最终可得到考虑有色噪声的惯导误差系统方程为：

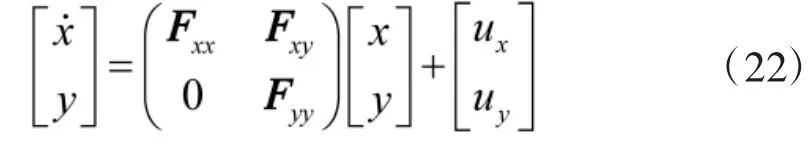
式中，y为新增系统状态，Fyy、Fxy分别为uc状态空间方程的系统矩阵和量测噪声矩阵，uy为uc状态空间的噪声，具体形式可参见文献［13］。

新系统噪声协方差矩阵可表示为

式中，Qx为未考虑有色噪声系统的噪声协方差矩阵，Qy为uc状态空间系统噪声，可由Timoshenko梁混合系统响应输出量的数字特征确定。

4 仿真试验与分析

结合某型飞行器惯导的具体几何安装尺寸和材料参数，取其陀螺仪的常值漂移为0.1（°）/h，随机漂移为 0.02（°）/h，加速度计初始偏差为 100 ug，随机偏差为50 ug，考虑由Timoshenko梁混合系统响应得到的有色噪声生成增强系统方程，对飞行器进行组合制导解算仿真。可以看到增强卡尔曼滤波导航算法稳定可行，在一定时长范围内，各误差参数均收敛未发散。同时将增强卡尔曼滤波与未考虑有色噪声的卡尔曼滤波算法进行对比，其位置解算误差对比如图5所示。

从整体上看，虽然误差结果相差不大，但增强卡尔曼滤波解算结果精度还是有所提高，同时从图中可也可以看到在部分时间段内，两种方法精度优劣度出现交错，一方面原因是因为滤波参数配置会导致收敛速度有所不同，另一方面原因是Timoshenko梁混合系统模型与实际情况仍有一定的差别，导致系统有色噪声的估计出现相应的误差。

5 结论

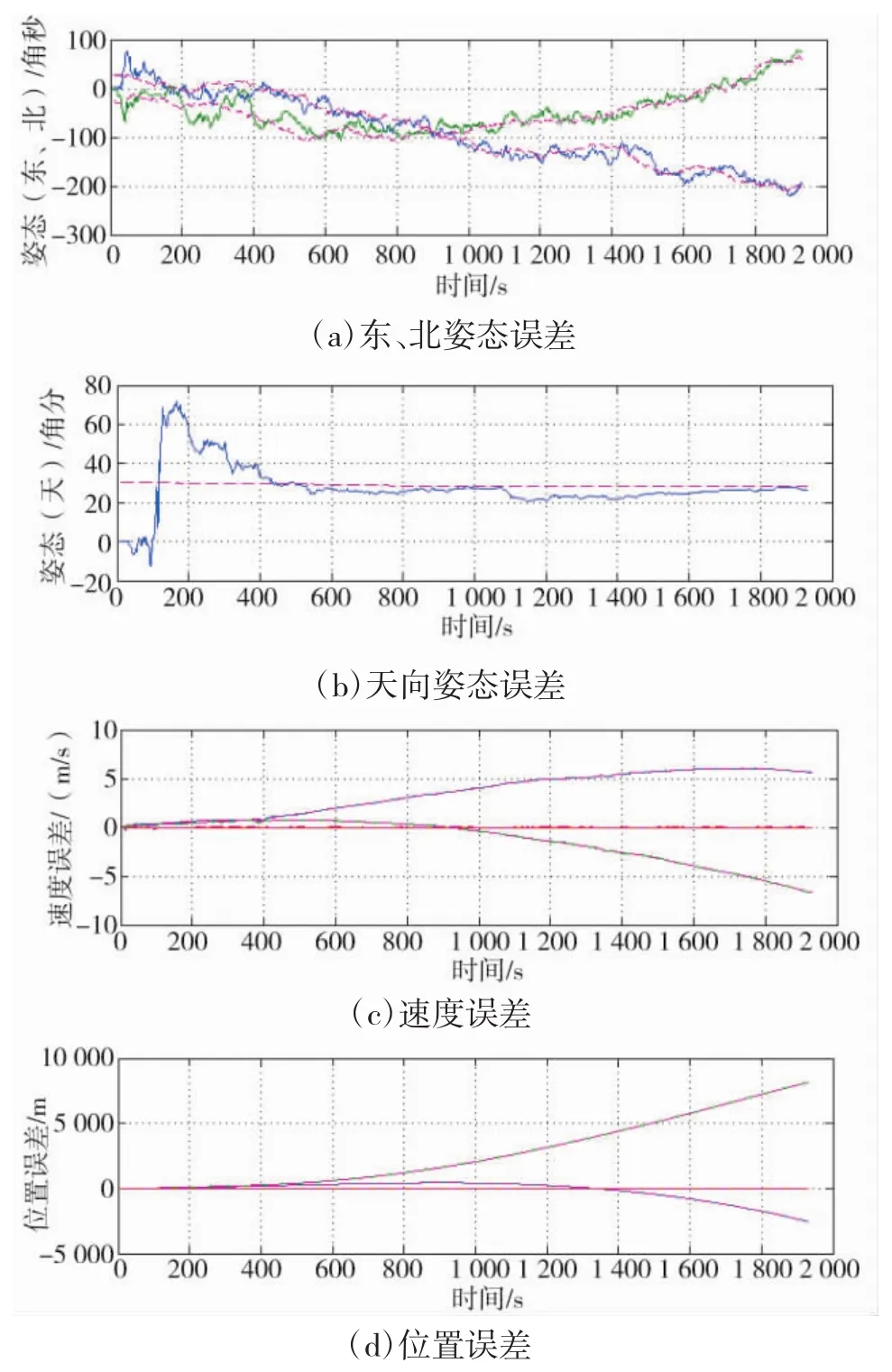
图3 增强卡尔曼滤波解算误差

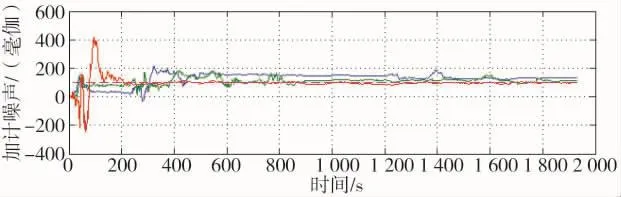
图4 加速度计噪声误差

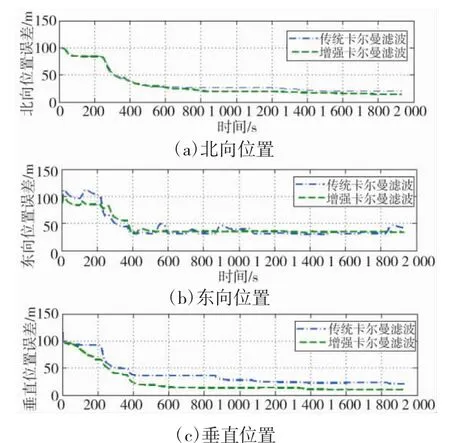
图5 滤波误差对比

通过建立Timoshenko梁混合系统模型求解响应输出，进而分离惯性仪表随机误差中的部分有色噪声，对其进行微分方程描述并导入到惯导系统误差模型中，利用增强的卡尔曼滤波算法可以提高解算的精确度。如果能获得接近实际工况条件下多场耦合的外部激励，对有色噪声分析将更为准确，同时惯性仪表随机误差中的其余组成部分，是值得进一步研究的问题。