基于微多普勒周期相关性的弹道群目标信号分离*

许 丹，田 波，冯存前，耿志远，董海力

（1.空军工程大学防空反导学院，西安 710051；2.空军工程大学航空航天工程学院，西安 710038；3.空军工程大学理学院，西安 710051）

0 引言

近年来，弹道导弹防御成为了各国研究的重点［1-2］。在弹道中段，母舱会释放各种目标，一般包括：弹头、轻重诱饵、姿态控制器、碎片、箔条等。这些目标在高速平动的同时，具有不同形式的微运动。其中弹头为保持稳定会进行自旋，在受到扰动后会保持进动；诱饵目标由于没有姿态控制一般处于摇摆状态；旋转目标会以一定的角速度进行旋转；碎片和箔条等小目标会随机高速翻滚［3］。这些目标信号在雷达回波中相互交叠，给真弹头信号提取带来了很大困难。为了有效提取各目标的参数信息，需要对群目标信号进行分离处理，见文献［4-6］。

然而上述方法的研究对象均未涉及到旋转目标与弹头信号的分离，因此，本文以旋转目标和锥体弹头为研究对象，提出了一种利用同一目标微动周期的相关性对群目标进行信号分离的方法。为了有效地分离出不同目标信号，对雷达回波进行了一系列的预处理，包括时频变换、SVD去噪、高斯平滑、Viterbi算法［7-8］曲线提取。再根据不同目标具有不同的微动周期、同一目标周期具有相关的特性，实现了群目标的信号分离。仿真结果验证了上述方法的适用性。

1 模型分析

1.1 进动目标模型

进动锥体目标模型如图1所示，锥体对称轴与锥旋轴交于o点，进动角为θ，进动角速度为ω1。雷达视线与锥体对称轴的夹角（姿态角）为β，与进动轴的夹角为α1（视线角）。当姿态角满足［11］时，能观测到 A、B、C 3 个强散射中心，当姿态角满足 β∈（0，π/2-ε）［11］，能观测到 A 和C两个强散射中心，O-XYZ为全局坐标系，o-x0y0z0为弹体坐标系，z0轴为目标自旋轴的指向，o-x'y'z'为相对坐标系，且o-x'y'z'平行于O-XYZ。

当弹道目标来袭时，由于遮挡效应雷达在大部分时间内仅可以观测到两个散射中心，因此，研究两个散射中心下的目标微动特性更具有实际意义。

在高频近似的条件下，目标呈光学区散射特性，目标回波可等效为几个强散射中心回波之和［12］，通过几何推导可得姿态角 β（t）满足式（1），其中 φ0为初相。

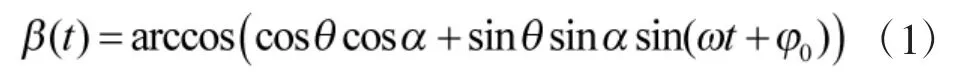
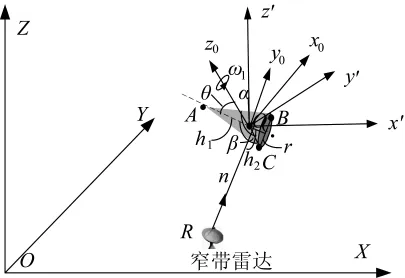
图1 雷达观测示意图

设散射中心A和C在相对坐标系中的坐标分别为（xA，yA，zA）和（xC，yC，zC），则由进动导致散射中心位置走动距离可以表示为：

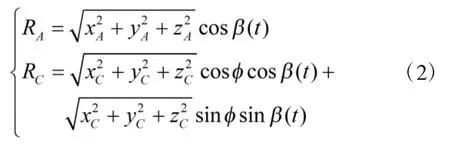
1.2 旋转目标模型

旋转目标模型如图2所示，以旋转目标上的散射中心P为例进行分析。假设目标质心为O'，以质心O'为坐标原点建立与全局坐标系平行的相对坐标系（x''，y''，z''）。目标的旋转角速度为 ω2，O'N 为旋转轴，与雷达视线的夹角为α2，φP为初始方位角，定义t时刻目标的旋转矩阵为Tr，设t=0时，P在相对坐标系中的坐标为：rP=（xP，yP，zP）T。

图2 旋转散射中心示意图

经过数学公式推导，可求得的旋转导致散射中心P走动距离为：

1.3 窄带模型

假设雷达发射单频脉冲信号，经正交双通道解调可以得到回波基带信号为：

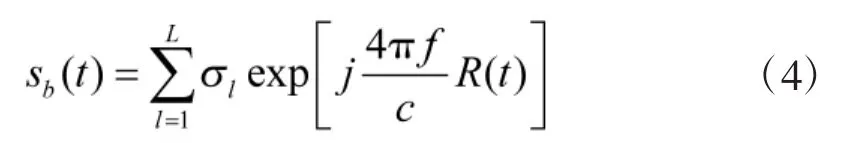
其中，f为载波频率，c表示光速，R（t）表示微动导致散射中心走动距离。对式（4）进行时频分析可得散射中心微多普勒变化式：

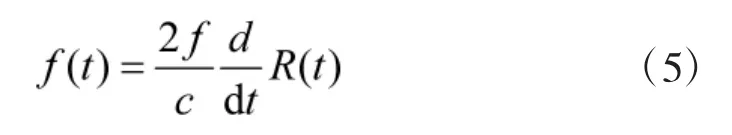
2 回波处理

雷达回波中含有目标运动和结构信息，为了更好地提取参数，需要对回波进行时频变换、降噪平滑、曲线分离等预处理。

2.1 时频变换

由式（5）可知，雷达回波的时频表达式中含有散射中心参数信息，可通过提取时频曲线参数来实现目标散射中心参数获取。关于时频变换的选取，本文采用短时傅里叶变换。短时傅里叶变换使用一个很窄的窗函数取出信号，并求其傅里叶变换。令g（t）为一个时间宽度很短的窗函数，让其沿时间轴进行滑动。于是，信号x（t）的短时傅里叶变换定义为：

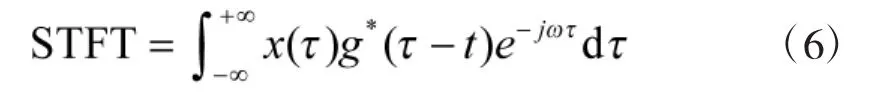
2.2 降噪平滑

时频变换后的时频图上不仅存在着目标信号，还存在着大量的噪声。为了提高参数提取精度，需要对时频图进行降噪处理。传统的图像降噪方法是使用不同频域的滤波器进行降噪，在图像频域分布未知的情况下，该方法会造成图像的部分失真。相较与滤波器降噪，奇异值分解（SVD）作为一种新型的非线性滤波算法，从图像矩阵的角度出发，对矩阵进行奇异值分解，噪声信息表示为较小的矩阵奇异值，而时频图中大部分目标信息则对应较大的矩阵奇异值，因而可以通过其中较大奇异值对应的矩阵向量进行重构，实现图像噪声的滤除。为了避免信号消噪后，时频平面上出现的曲线“毛刺”对曲线分离的不利影响，再对时频图进行平滑处理。

2.3 微多普勒曲线分离

群目标的微多普勒曲线受到微动参数、结构参数和雷达视角的调制，不同目标对应的调制特性也各不相同，在时频图中会出现不同程度的交叠，Viterbi作为一种寻找序列隐状态的动态规划估计算法，可以从时频图中估计出各分量信号的瞬时频率。瞬时频率估计最小化的表达式为：

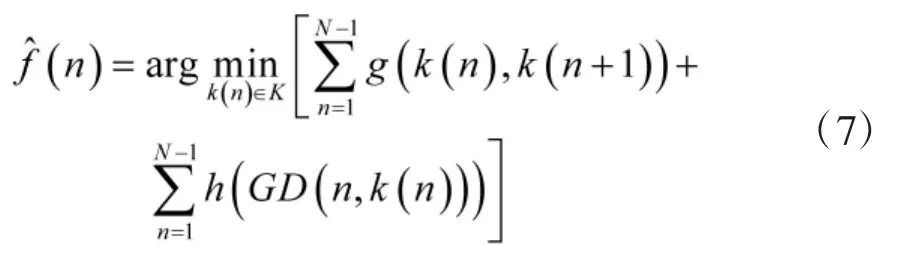
其中，N为采样点数，k（n）为时频图上某条曲线的路径，k为在整个时频分布中所有可能的路径集合，g（x，y）=g（|x-y|）为|x-y|的惩罚函数，表示两个时刻的瞬时频率变化，h（x）为 GD（n，k（n））的惩罚函数，表示该时刻频率点的重要程度。在对时频图进行SVD去噪和高斯平滑处理后，采用Viterbi算法在高噪声条件下也能很好地提取出各时频曲线。

由式（2）可知，锥顶散射中心微多普勒满足正弦规律，周期为2π/ω1，底面散射中心微多普勒变化不满足标准的正弦规律，但满足相同的变化周期；旋转目标上的散射中心具有相同的旋转周期2π/ω2。通过上述分析可知，同一目标上的散射中心具有相同的变化周期，不同目标上的散射中心不具有这种相关性，因此，可根据群目标周期相关性对其进行分离。

综上所述，对雷达信号图像处理的具体实施流程图如图3所示。

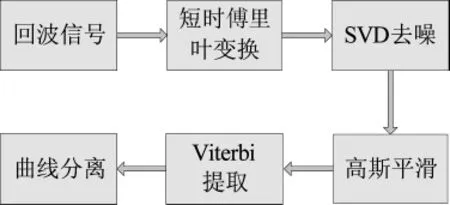
图3 图像处理流程图

3 仿真分析

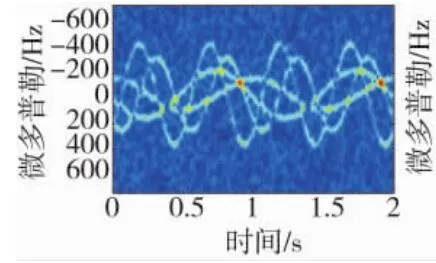
图4 原始回波时频图

图5 SVD消噪图

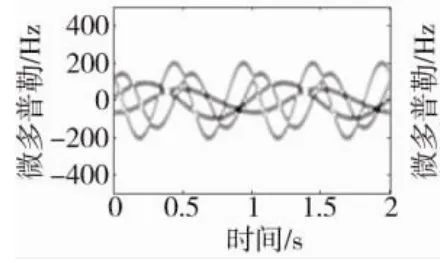
图6 平滑处理后时频图

图7 Viterbi提取时频曲线结果

图8 提出曲线后的傅里叶变换

群目标参数设置：假设群目标中有一个锥体弹头目标，一个旋转目标，锥体目标可观测到散射中心A和C，旋转目标可观测到散射中心P1和P2。散射中心A和C在相对坐标系中的坐标分别为（-0.8，-0.6，1.4）、（-0.5，-0.3，-0.6），进动角 θ=10°，锥旋角速度ω1=4πrad/s，P1和P2散射中心在相对坐标系中的坐标为（0.3，0.2，0.5）、（-0.3，-0.3，-0.5），散射中心旋转角速度为ω2=2πrad/s。窄带雷达参数设置为：载频f为8 GHz，雷达脉冲重复频率为1 000 Hz，观测时间2 s，信噪比为5 dB，雷达视线与进动轴的夹角为 α1=50°，与旋转轴的夹角为 α2=80°。

图4为采用短时傅里叶变换得到的原始回波时频图，可以明显地看出散射中心时频曲线呈周期变化，同时可以看到时频图中含有大量噪声。图5为采用SVD消噪后的处理图，可以看出噪声得到了很好地抑制。时频图像中的曲线并不光滑，为了避免曲线“毛刺”对曲线分离的不利影响，对时频图进行平滑处理，平滑处理的结果如图6所示。图7为采用Viterbi算法提取出的时频曲线，可以看出提取的曲线能够很好地反映时频曲线的变化规律，方便后续的傅里叶变换。图8为对提取出的曲线经过FFT变换后滤除零频分量的结果，可以看出曲线1和曲线2在频率为2 Hz处具有峰值，可将这两条曲线归为一类目标，同理曲线3和曲线4归为一类目标。由此可知，群目标中有两个目标，目标的周期为0.25 s和1 s。若需要对曲线参数进一步提取，可利用Hough变换和Radon变换，在此不具体阐述。

4 结论

本文以弹道群目标为研究对象，研究了多散射中心微多普勒曲线分离问题。在获取目标时频图的基础上，对时频图进行了SVD消噪、高斯平滑、Viterbi提取曲线、傅里叶变换，最后根据目标周期的相关性分离出了群目标信号。仿真结果表明，所提方法能够较好地分离出群目标信号，下一步将验证本文算法在复杂群目标中的分离效果。