独立转向与驱动无人装甲车操稳性分析*
谢 磊,杜忠华,王 腾,周光东
(南京理工大学机械工程学院,南京 210094)
0 引言
近年来,随着通信技术和互联网技术的迅速发展,全电驱动无人车辆领域应运而生,各大车企包括涉及军用车辆的军工企业和高校纷纷投入研究[1]。三轴军用全电驱动无人车辆一般以轮毂电机驱动,以蓄电池供电,与传统车辆相比,其簧下质量增加,驱动方式改变[2]。基于以上特点,其整车操纵稳定性便成为研究重点。为了改善其操纵性能,四轮转向技术是一种最常见的改善汽车操纵稳定性的底盘控制技术[3]。随着计算机控制技术的进步,线控转向技术的开发与应用正在成为现代汽车技术发展的重要方向[4]。为此,本文自行设计了一种基于蜗轮蜗杆传动的一体化线控独立转向-悬架机构系统[5],可适用于各种独立转向的情况,转向角范围达±90°,可实现侧向平移和原地旋转等运动,运动轻便灵活。为了提高此无人装甲车的操纵稳定性能,利用虚拟样机技术,基于多体系动力学理论,在ADAMS/Car中建立了线控独立转向与驱动无人装甲车辆的各子系统模型,由相应的通讯器建立整车动力学模型[6]。参照国家相关标准完成6项操纵稳定性仿真试验和实车试验[7],根据实车试验数据验证了仿真结果的正确性。然后,通过分析线性二自由度理论模型推出瞬态响应影响因素并进行转向盘角阶跃输入试验对其定量分析[8]。最后,通过优化后建立的新虚拟样机模型对整车操纵稳定性进行重新评价。结果表明优化后在一定程度上改进了车辆的瞬态响应特性,车辆的操纵性能得到相应的提升。证明对线控独立转向与驱动无人装甲车的瞬态响应改进有效,仿真结果具有较高的可信度,为今后三轴轮式军用车辆的瞬态响应特性的改进提供参考。
1 整车虚拟样机的建立
1.1 建立整车仿真模型
根据自行设计的一款线控独立转向与驱动无人装甲车辆样车数据,运用多体动力学软件ADAMS/Car建立线控独立转向与驱动无人装甲车辆整车虚拟样机模型,其主要参数如表1所示。该整车动力学模型由车身子系统、悬架子系统、转向子系统、轮胎子系统、动力传动总成子系统等组成[9]。由于转向系统蜗轮蜗杆式转向机构的蜗杆支座与车身固定连接,因此,必须在车身系统建立正确的通讯器,以确保车身子系统和转向子系统正确装配。悬架子系统中前、中、后悬架采用自主设计悬架,所建立的悬架子系统,如图1所示。为了提高整车的操纵稳定性能,在前轴、中轴和后轴中,通过蜗轮蜗杆实现全轮转向,其中,蜗轮安装在悬架减震器外轴上,蜗杆的支座固定在车身上,两者啮合实现全轮转向。车轮转角的大小是由相应的转向机构中蜗轮蜗杆啮合的线位移决定,其大小由不同的控制策略给定。在轮胎的属性文件中改变轮胎的刚度属性,从而建立符合条件的轮胎子系统。最后由相应的通讯器建立整装虚拟样机,如图2所示。

图1 线控独立转向与驱动无人装甲车辆悬架

图2 线控独立转向与驱动无人装甲车整车虚拟样机模型

表1 装甲车模型部分参数
1.2 模型仿真与样车试验验证
基于无人装甲车虚拟样机模型,参照国家相关标准完成了6项操纵稳定性试验,并根据结果对其操纵稳定性能进行评价[10],最后将仿真结果与实际样车试验结果进行对比,如表2所示,仿真结果与试验结果最大差别为5.2%,多体动力学仿真模型的精确度得到验证。
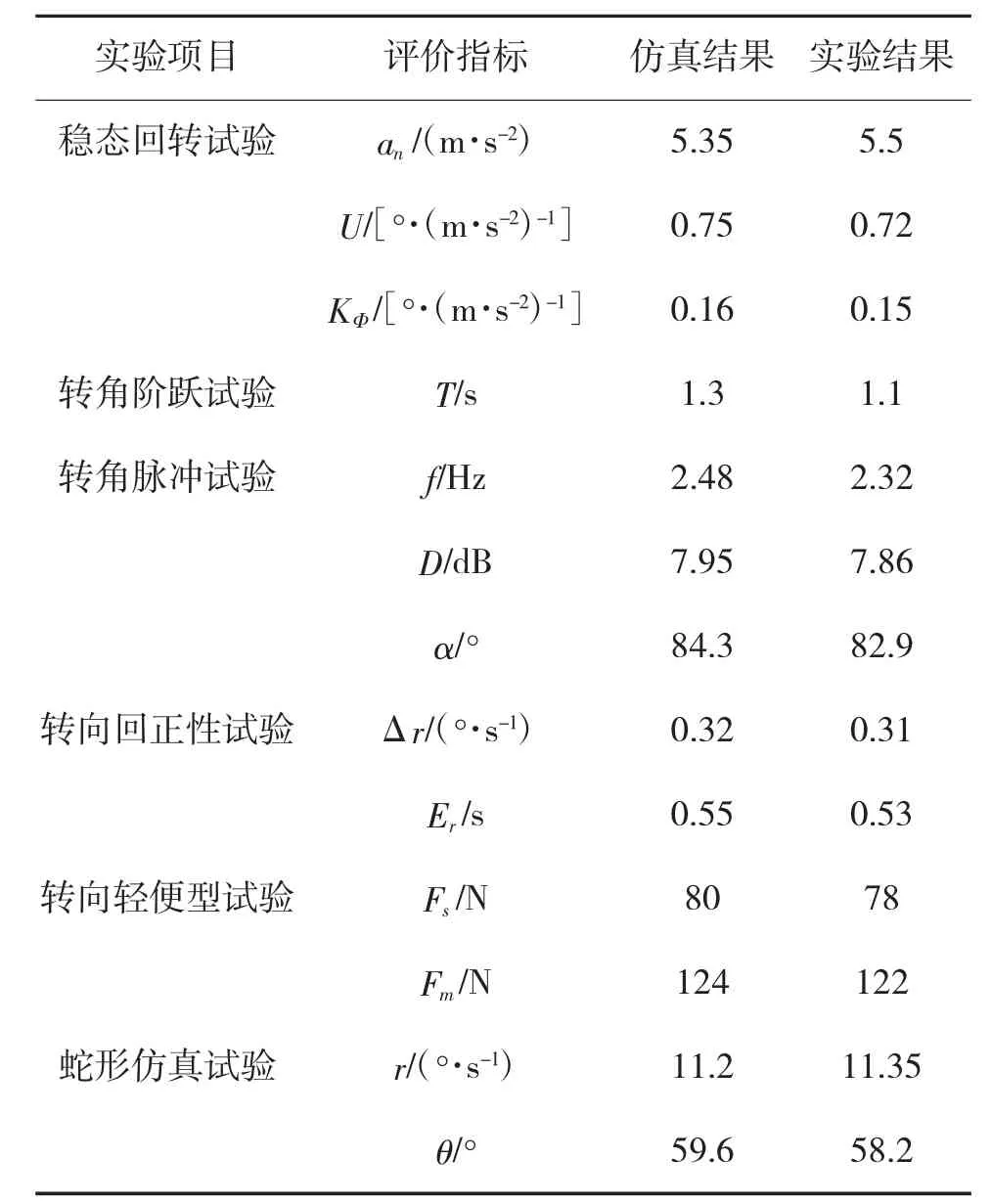
表2 操纵稳定性仿真结果与实际试验结果
2 瞬态响应影响因素的仿真试验与分析
2.1 线性二自由度车辆模型
为了分析线控独立转向与驱动无人装甲车转向时的横摆角速度瞬态响应特性,建立其线性二自由度简化模型[11],如图3所示。以整车的质心为原点建立xyz-O笛卡尔坐标系,x轴平行于地面其正方向指向前进方向,y轴正方向指向驾驶员的左侧,z轴通过质心指向上方。假设装甲车关于xOz平面对称,O是装甲车的瞬时转向中心。模型有2个自由度:整车沿y轴的侧向运动和绕z轴的横摆运动。
经分析得无人装甲车二自由度运动微分方程:

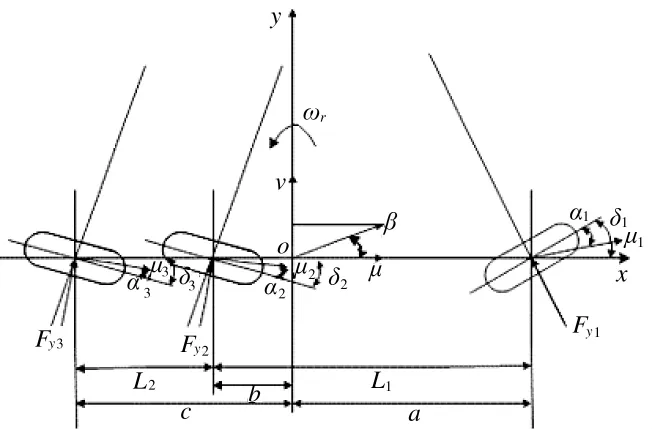
图3 无人装甲车二自由度模型
式中,m为整车质量;ν为质心侧向速度;μ为质心前进速度;wr为横摆角速度;Kα1、Kα2、Kα3分别为前轮、中轮和后轮综合侧偏刚度;β为质心侧偏角;a、b、c分别为质心至前轴、中轴和后轴的距离;α1、α2、α3分别为前轮、中轮和后轮侧偏角;δ1、δ2、δ3分别为前轴、中轴和后轴的转角;Iz为绕z轴的转动惯量;L1、L2为前中轴和中后轴的轴距;Fy1、Fy2、Fy3分别为前轮、中轮和后轮轮胎侧向力。
2.2 影响瞬态响应各因素仿真分析
根据式(1)分析,本款线控独立转向与驱动无人装甲车轴距和轮胎侧偏刚度是对整车操纵稳定性影响较大的变量;此外整车轮距、质心位置等参数也是影响整车操纵稳定性的次要因素。在此不作分析。为分析无人装甲车轴距和轮胎侧偏刚度对瞬态响应的具体影响,利用所建动力学模型进行仿真分析。仿真过程中无人装甲车车速为80 km/h,在这个车速下侧向加速度2 m/s2对应的方向盘转角为15°。
2.2.1 轴距变化对瞬态响应的影响
如图3所示,以无人装甲车质心为坐标原点,质心与前轴的距离x1=1 600 mm,对无人装甲车进行角阶跃输入下的稳态响应仿真,表3中试验1~9分别对应图4、图5中曲线C1~C9。不同前中轴距对应的横摆角速度响应曲线如图4所示,不同中后轴距对应的横摆角速度响应曲线如图5所示。
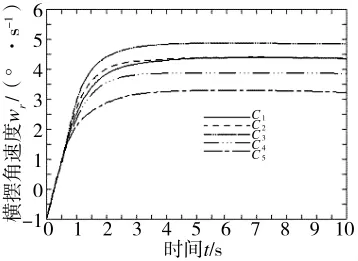
图4 不同L1对应的横摆角速度响应曲线

图5 不同L2对应的横摆角速度响应曲线
从图4中曲线C2与C1对比可以看出,质心位于中轴与后轴之间时,横摆角速度的稳态值并没有变化,但稳定时间更短说明其转向灵敏度相对提高。而曲线C3、C4、C5则说明质心位于前轴与中轴之间时,前中轴距越长车身横摆角速度的响应稳态值越小,从图5中曲线可以看出中后轴轴距越大,横摆角速度稳态值越小。这一结论与二自由度模型的分析结果一致。为对比不同参数变化对响应速度的影响分别计算横摆角速度的响应时间 、峰值响应时间ε、稳定时间σ、超调量ψ。得出不同轴距对应的转向盘阶跃输入响应指标值如表3所示。
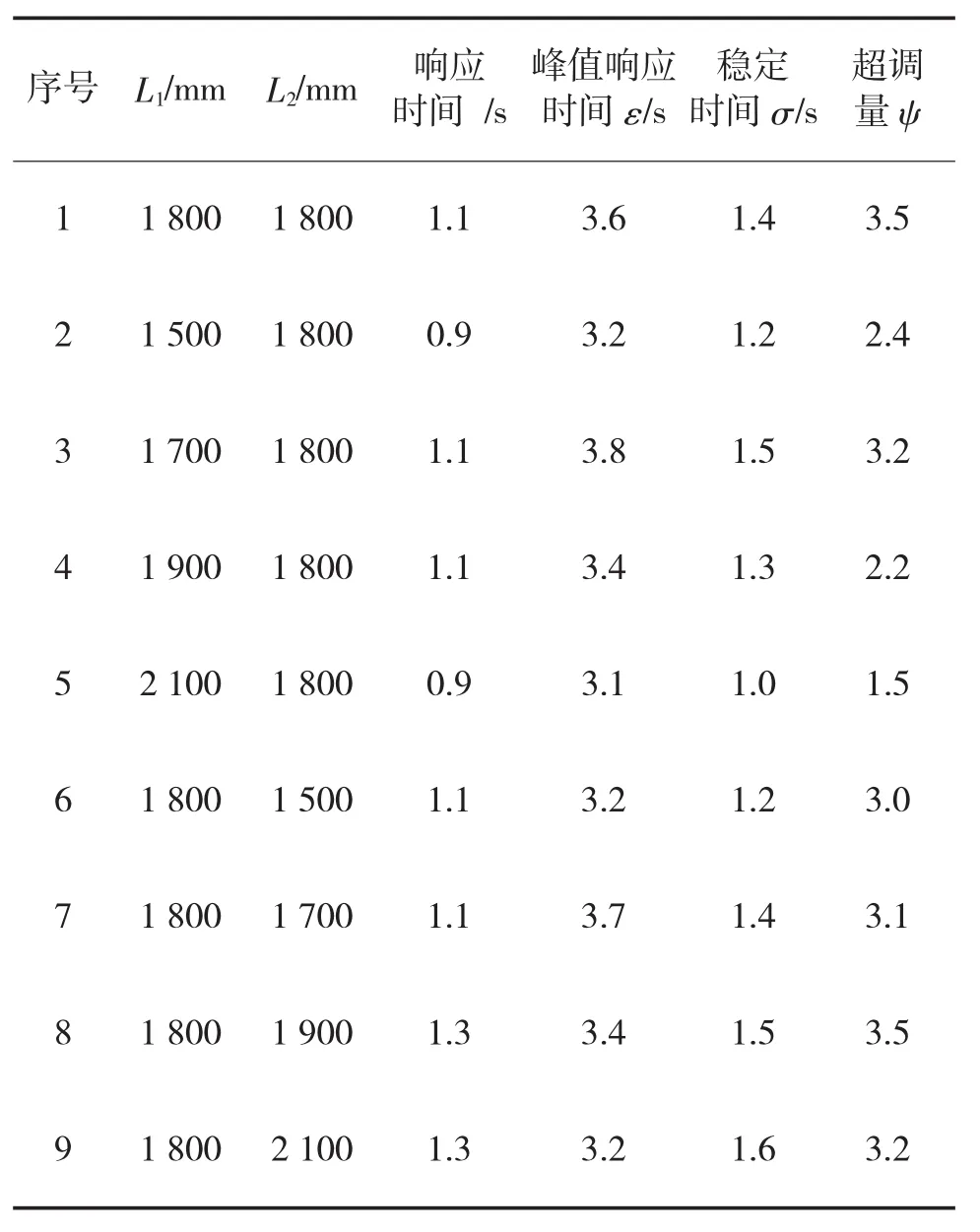
表3 轴距对转向盘角阶跃输入横摆角速度响应的影响
2.2.2 轮胎刚度变化对瞬态响应的影响
同样对轮胎刚度变化对阶跃输入响应的影响进行仿真计算,由于PAC2002轮胎模型[12]中利用垂向刚度以及轮胎特性曲线的特征系数来计算轮胎侧向力。则用比例系数i来表示轮胎垂向刚度的变化,表4中试验1~9分别对应图6、图7中曲线Z1~Z9。不同前轮轮胎垂向刚度对应的横摆角速度响应曲线如图6所示,不同中后轮轮胎垂向刚度对应的横摆角速度响应曲线如图7所示。
图6中曲线说明前轮垂向刚度减小,横摆角速度稳态值减小。图7中曲线说明中后轮垂向刚度越大横摆角速度响应稳态值越小,图中稳态响应特性的相关参数如表4所示。
从表4中数据可以看出,轮胎垂向刚度变化对横摆角速度响应的影响不太明显。但从图6和图7中可以看出基本符合前轮刚度越小后轮刚度越大,稳态值越小的规律。

图6 不同前轮轮胎垂向刚度对应的横摆角速度响应曲线

图7 不同中后轮轮胎垂向刚度对应的横摆角速度响应曲线

表4 轮胎刚度对转向盘角阶跃输入横摆角速度响应的影响
3 优化后操纵稳定性评价
综合前面的分析结果,为提高车辆瞬态输入响应可以加大前中轴距,缩短中后轴距。而太大的后轮侧偏刚度则会造成车辆的过多转向,因此,前中轴轴距不能设计的过大。其次考虑到本车质心位置相对居中,为避免三轴轴荷差别过大将前中轴轴距增大为2 000 mm,中后轴轴距缩短为1 600 mm,增大轮胎刚度为原来1.2倍。建立新的系统模型装配到整车系统中进行仿真计算。为了方便对比优化前后效果,对优化后的虚拟样机模型依次进行各项操纵稳定性评价试验,通过评分结果定量说明优化的效果。
从下页表5中可以看出,优化方案对稳态回转、蛇形试验评分的改进效果并不明显。平均横摆角速度峰值减小,评分有所提高,说明优化在一定程度上改进了车辆的瞬态响应特性。总的来说,根据分析结果优化后车辆的操纵性能有了一定程度的提升,尤其是瞬态响应性能有了明显的提高,但在稳态回转、蛇形试验等综合工况下的性能没有明显提升。

表5 操纵稳定性仿真结果优化前后对比
4 结论
本文针对课题组预研项目某军用全电独立驱动无人装甲车在实际研发过程中遇到的操纵稳定性能欠佳问题进行改善优化,提出了相应的优化方案,采用多体动力学方法,建立虚拟样机仿真模型,并结合试验验证了优化方案的可靠性。
1)自行设计了一种基于蜗轮蜗杆传动的一体化线控独立转向-悬架机构系统,实现全轮转向,并基于ADAMS/Car建立其整车多体动力学仿真模型。
2)通过参数的灵活调整,找到影响瞬态响应的敏感因素,并对影响参数进行定量分析,找出轴距与轮胎刚度变化对瞬态响应影响规律。
3)综合考虑各方面因素,增大轮胎刚度为原来1.2倍,前中轴轴距增大为2 000 mm,中后轴轴距缩短为1 600 mm,对优化后的虚拟样机模型依次进行各项操纵稳定性评价试验,通过评分结果定量说明优化的效果。
此外,整车轮距、质心位置等影响整车瞬态响应的次要因素在本文未作深入分析,需进一步研究。

