基于盐岩腔体收敛过程的地表变形动态预测

童 凯，杜圣贤，贾 超，狄胜同，马玉骁

(1.山东大学土建与水利学院，山东 济南 250061；2.山东大学海洋地质与工程研究所，山东 青岛 266237；3.山东省地质科学研究院，山东 济南 250013)

0 引 言

盐岩因其易溶于水，所以水溶开采盐矿是一种十分便捷经济的方案。又因具有极低的渗透率、良好的损伤自愈能力和塑性变形大等优良特性，被全球各国广泛的运用在石油、天然气等资源的储备上。

在盐岩力学特性研究方面，杨春和等[1]、YANG等[2]、WANG等[3]、姜德义等[4]、HOU等[5]学者开展了诸多研究，这对掌握盐岩特性十分重要。由于盐岩的流变特性，使得盐腔在运营过程中会发生收敛，进而引发地面沉降，威胁到地表建筑物的安全[6]。由此可见研究引起地表沉降的机制对于控制由于盐矿开采引发的次生地质灾害十分必要。然而我国在地下矿产开采引起地表沉降的研究方面起步较晚，刘宝琛等[7]最先引进并发展了概率积分法，并在煤矿地表变形预测中进行了运用。任松等[8]又将用于煤矿开采沉降计算中的概率积分法引入到盐岩的沉降预测中，并根据该理论发展了新概率积分三维预测模型。李银平等[9]利用半无限域内球形空洞受力收缩位移解，利用叠加原理得到考虑内压作用下的地表沉降弹性积分解析解。陈雨等[10-11]采用Gaussian曲线表示沉降分布，结合腔体收敛函数，建立了传递函数法预测地表变形的理论在此基础上综合考虑影响腔体收敛的多种时效因素(腔体水溶速率、体积收敛系数以及收敛传递率等)，根据SCHOBER等[12]提出的两阶段收敛模型，建立了一套较为完整的变形动态预测方法。

基于传递函数建立的动态预测模型是一套较完整的用于求解盐矿开采诱发地表沉降的计算模型，但模型中收敛系数和传递率对于地表沉降的动态预测影响较大，其值估计的准确性直接决定了地表沉降结果的准确性。因此，本文基于传递函数方法和幂指函数模型，在考虑腔体收敛过程的情况下，对腔体收敛形式进行合理的简化，建立起一套适用于预测盐岩开采诱发地面变形的动态预测模型。

1 腔体收敛变形理论模型

1.1 传递函数模型

传递函数模型考虑地下腔体收敛与地表变形之间的联系，认为腔体临空边界所受应力以水平方向为主，假设其受力过程中水平方向的变形远大于垂直方向的变形，从而建立起地下腔体收敛与地表变形之间的函数[10]，见式(1)。

式中：S(x,y)为地表沉降分布函数；a为考虑收敛体积经上覆岩层传递折减后到达地面形成的沉降体积与溶腔体积之比；G(x,y)为联系地下腔体收敛和地表变形的关系函数；q(z)腔体收敛函数；zt、zb分别为腔体顶部和底部埋深。

1.2 收敛函数公式推导

基于传递函数法建立的动态预测模型可以运用于求解地面沉降问题[10,12]，详见式(2)～(4)。

(2)

F(ζ,η,t′)=

式中：S(d,t)为距离腔体中心d处在t时刻的沉降量；Sm为腔体中心处的最大沉降量；d为计算点到腔体中心的距离；r～2=rt×rb，rt、rb其中分别是溶腔顶部和底部的影响半径；T为建腔时间；ζ为收敛系数，η为传递率。

该模型在进行计算时，由于ζ、η参数的取值决定了计算结果的精度，而该参数又不易获得，为减小这一影响，本文在此基础上对腔体收敛过程进行一定合理简化，建立一套新的计算模型。

假设腔体建成后运行t时刻时，腔体体积满足式(5)关系。

V(t)=ψV0(5)

式中：V0为腔体建腔时体积；V(t)为t时刻收敛后的腔体体积；ψ为体积收敛率。

假设腔体收敛时主要发生水平方向的变形，而忽略垂直方向的变形。以圆柱形、椭圆形和梨形腔体为例，建立单腔变形预计模型，见图1。利用图1中的模型参数，根据腔体收敛的假设，便可以建立腔体的收敛函数q(z)。

图1 腔体收敛模型Fig.1 Convergence model of salt cavern

椭圆形腔体收敛前后的椭圆可描述为式(6)～式(7)。

(6)

式中：Δr为腔体收敛半径；B为椭圆形短半轴；A为椭圆形长半轴；zm为椭圆形腔体中心埋深。

将椭圆形腔体体积计算公式带入式(5)可得式(8)。对于整个椭圆形，收敛体积可表达为式(9)。联立式(6)～(9)，可得式(10)。

(8)

同理可得圆柱形腔体和梨形腔体的收敛函数,分别表达为式(11)和式(12)。

q(z)=π(1-ψ)×

式中：Zm为梨形腔体上下腔分界线埋深；h1、h2分别为梨形腔体上下腔高度；Rp为梨形腔体上下腔分界线处半径。

1.3 沉降函数推导

利用高斯分布函数描述地下收敛与地表变形的传递函数[10]，见式(13)。

(13)

式中：R为腔体开采在的地表影响半径，R=zcotγ；d为沉降计算点到腔体中心在地表的水平投影距离；γ为收敛影响角，一般小于45°[12]。

定义式(14)，并联立式(10)～(12)和式(14),可以求得三种不同形状腔体的地表沉降预测公式。圆柱形腔体地表沉降预测表达式见式(15)；椭圆形腔体体地表沉降预测表达式见式(16)；梨形腔体体地表沉降预测表达式见式(17)。

(14)

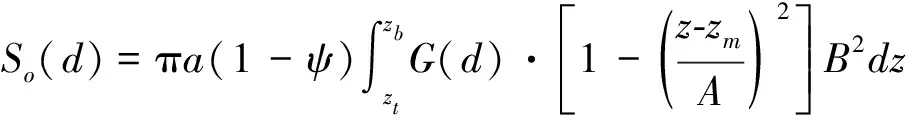
1.4 地表沉降与水平变形关系

地表沉降和地表水平变形之间的关系可用式(18)表示[6]。

(18)

式中，n为水平变形影响系数，可由现场监测数据所得，一般简化计算取n=1。

考虑腔体收敛过程，并由此可以得到三种不同腔形开采下地表的水平变形计算公式。定义式(19)，圆柱形腔体的地表的水平变形计算见式(20)；椭圆形腔体的地表的水平变形计算见式(21)；梨形腔体的地表的水平变形计算见式(22)。

(19)

Uo(d)=

当式(15)～(17)和式(20)～(22)中的ψ=0时，即此时储气库完全收敛，地表变形达到最大值。故式(15)～(17)和式(20)～(22)可统一表达为式(23)。

S=S0(1-ψ)(23)

式中：S0为腔体完全收敛的地表变形值；S为当腔体收敛率为ψ时的地表变形值。

至此，针对不同形状单腔开采考虑腔体收敛过程的地表沉降变形预测公式已经全部给出。

1.5 地表沉降动态预测模型

地下采空区的存在势必会对地表的建筑物和居民造成安全隐患[13]，而盐岩的蠕变特性又使得地表变形随着储库的运行持续变化。在煤田开采条件下，地表移动过程可从6个月延续到数年，而在盐矿开采条件下，移动持续时间甚至达到100年以上[14]。在储库运行初期还很难看出由于盐矿开采对地表建筑物的影响，但随着时间的推移，地表变形部分受压区可能会在移动期间遭受拉伸，反之亦然。因此在储库建设过程中除了考虑稳定后的地表变形状态，还须考虑地表变形随时间的发展过程[15]。

地表变形预测公式中，体积收敛率ψ随着储库运行时间的不同取值也不同，若知道不同时刻腔体的体积收敛率即可求得不同时间的地表变形分布。目前确定腔体收敛体积主要有以下三种方法：现场声呐测腔、数值模拟和工程经验预测。考虑到现场声呐测试的花费较高，又具有一定的滞后性，而经验预估又具有很大的不确定性，因此在条件有限的情况下采用数值模拟进行求解腔体收敛体积是一个较为可行的办法。

2 地表变形算例分析

2.1 计算模型及参数说明

为了验证本模型的预测效果，笔者在Matlab中编写了相应的计算程序，用以求解地面变形分布，同时运用Ansys建立相应的有限元模型，在FLAC3D中进行计算求解，将二者的计算结果进行对比。

本次仅针对椭球体单腔开采引起的地面变形进行预测，根据杨春和等[16]的研究成果，腔体采用长短轴为7∶3的椭球体模型。腔体取长半轴为70 m，短半轴比为30 m，腔体中心埋深1 000 m，各地层覆存深度及有限元模型见图2。数值模拟的瞬时稳态性计算采用Mohr-Coulomb弹塑性模型，蠕变计算采用FLAC3D自带的Cpower蠕变模型。参考文献[17]和文献[18]取各地层岩性及蠕变参数，详见表1和表2。

图2 岩层分布及有限元模型Fig.2 Rock strata distribution and finite element model

表1 各岩层力学参数Table 1 Mechanical parameters of each rock layer

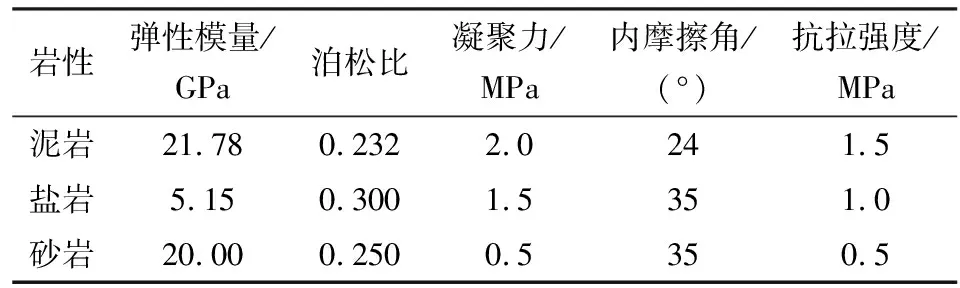
岩性弹性模量/GPa泊松比凝聚力/MPa内摩擦角/(°)抗拉强度/MPa泥岩21.780.2322.0241.5盐岩5.150.3001.5351.0砂岩20.000.2500.5350.5

表2 盐岩蠕变参数Table 2 Creep parameters of salt rock

模型计算中相关参数参考之前学者研究和经验进行取值，沉降预测公式中的a取0.8，影响角取37°。数值模拟直接从腔体运营期开始计算，暂不考虑腔体运行压力和建腔过程对于地表沉降的影响。假设腔体运行压力为0，虽然这将导致计算结果偏大，但对于储库设计考虑是偏安全的。

2.2 数值模拟与预测模型结果对比

通过数值模拟可以求得不同运行时间的腔体体积收缩量，再带入式(23)即可求得地表沉降变形的动态过程。

2.2.1 地表沉降动态曲线对比

根据数值模拟求出不同蠕变时间的腔体体积收缩量，再利用预测模型求取地表中心沉降值。以数值模拟的中心沉降值为标准，将预测模型和数值模拟的误差统计在表3中。

表3 盐腔地表中心沉降值计算表Table 3 Central surface subsidence of salt cavern

将数值模拟和预测模型的计算的不同蠕变时间的地表中心沉降值绘制在图3中，可以更直观地比较二者之间的关系。

从图3和表3中可以看出，预测模型和数值模拟的发展趋势基本相同。蠕变前10年二者相对误差较大，由于该阶段沉降值较小，即便绝对差值只有0.84 mm的第一年，相对误差也达到了18.8%，随着蠕变时间的增加，误差逐渐减小，蠕变50年时，相对误差仅有1.3%，整个计算周期内，最大沉降差值为1.4 mm，说明本预测模型具有较高的精度。

2.2.2 地表变形空间分布对比

为了进一步检验预测模型的地表变形在空间中的分布情况，计算储气库运行50年时，以数值模拟的地表变形值为标准，将预测模型和数值模拟的误差统计在表4中，将其与数值模拟的计算结果绘制在图4中。

图3 数值模拟和预测模型地表中心沉降对比Fig.3 Comparison of surface subsidence between numerical simulation and prediction model

表4 地表变形分布曲线对比Table 4 Comparison of surface deformation value

计算结果水平距离/m预测模型/mm数值模拟/mm相对误差/%0-19.89-19.641.3100-19.54-19.142.1200-18.50-17.972.9300-16.93-16.403.2400-14.93-14.453.3地表沉降/mm500-12.70-12.342.9600-10.43-10.172.6700-8.26-8.735.4800-6.32-7.019.8900-4.66-5.6617.71 000-3.32-4.2622.100.000.20-1001.961.970.52003.713.904.93005.095.466.84005.996.457.1水平变形/mm5006.366.877.46006.276.676.07005.796.338.58005.065.7912.69004.205.0316.51 0003.324.1019.0

从图4和表4中可以看出，数值模拟和预测模型计算的地表中心沉降最大值计算结果分别为19.64 mm和19.89 mm，相对误差仅为1.3%。在整个计算区域内，当径向距离小于600 m时，数值模拟的计算结果稍小于预测模型，但随着距离的增大，数值模拟的结果会偏大一些。当距离达到1 000 m时，由于地表沉降值已经很小，即使只有0.94 mm的差值，相对误差也达到了22.1%。

分析水平变形分布曲线和误差统计可以得出，地表水平变形最大值发生在径向距离为500 m的位置，二者计算的最大值分别为6.36 mm和6.87 mm，相对误差7.4%，计算结果很接近。径向距离小于700 m时，二者的相对误差均小于10%，但随着径向距离的增大，很明显数值模拟的计算结果较预测模型稍大，最大误差达到了19%。

综合地表沉降和水平变形分布曲线的对比结果，可以得出以下结论，本文所提出的预测模型计算的地表变形空间分布规律和数值模拟一致，但在距离腔体中心较远时，预测结果存在一定误差。但主要关心的变形较大的集中区域拟合程度较好，因此在一定条件下能满足工程精度需求。

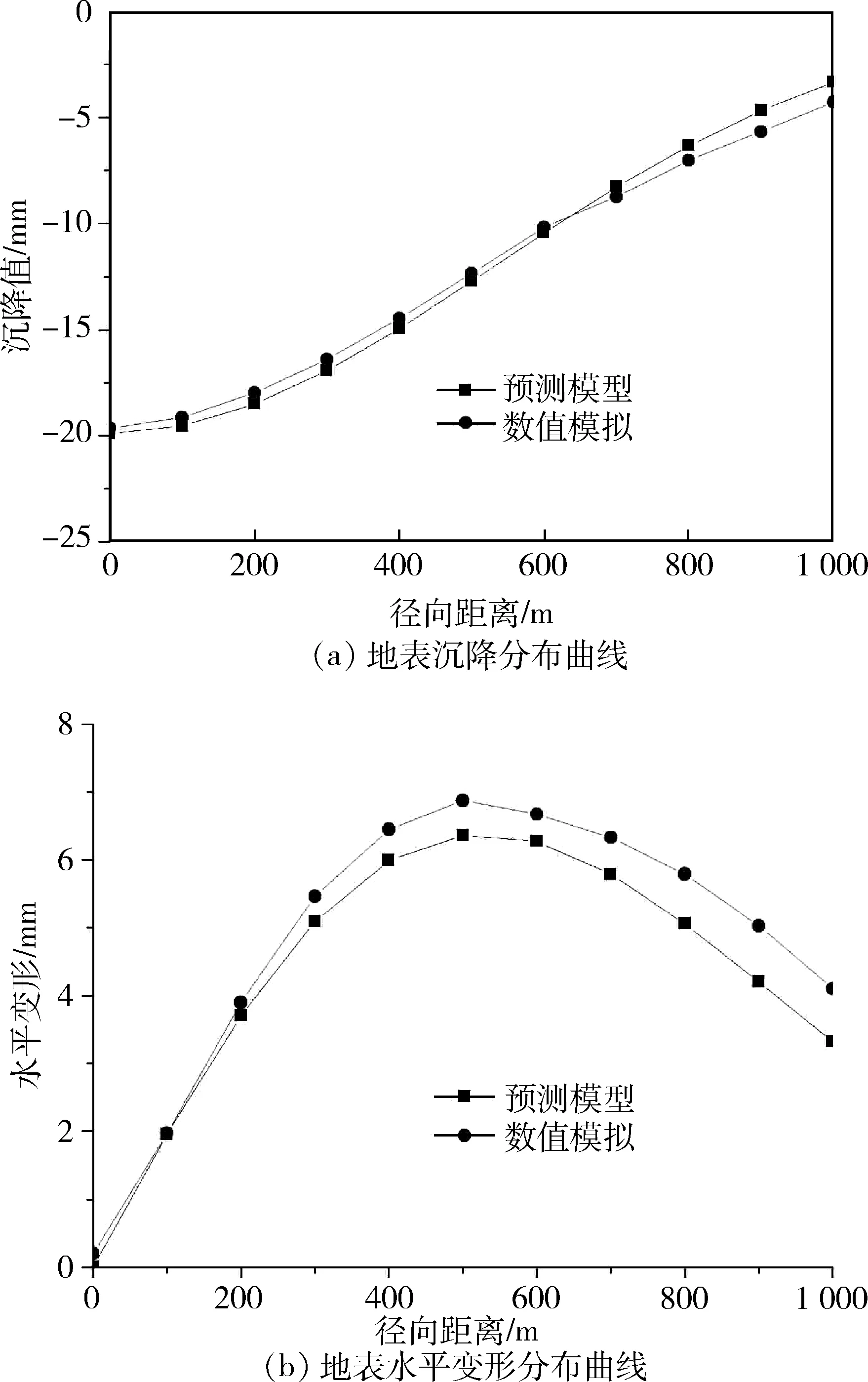
图4 储气库运行50年地表变形对比Fig.4 Comparison of surface deformation in operation for 50 years of gas reservoir

2.3 群腔地面变形动态预测

为了保证地表变形在可接受范围内，尽可能多地开采盐岩，充分利用盐矿资源，使有限空间内的经济效益达到最大化，实行群腔开采。运用本文提出的地表变形动态预测模型，再利用叠加原理进行群腔的地面沉降动态预测，假设各腔体沉降计算的参数相互独立[12]，则地表任一点p(xi,yi)的变形值可由式(24)表达。

(24)

式中：Sp(xi,yi)(t)为点p在t时刻的地表沉降值；di为点p到i号腔体的径向距离。

各地层分布情况及腔体形状和图2相同，开采形式如图5所示，邻腔夹角60°，腔距为2.0D[19]。基于叠加原理的假设可知，各腔体之间的变形互不影响，故以表3中的腔体收敛率作为该算例中各腔体的收敛动态过程，将地表沉降结果绘制在图6中。

图5 群腔布置平面图Fig.5 Plan position of salt caverns field

图6 群腔开采地面沉降曲线Fig.6 The subsidence curve of salt caverns

采用图5所示盐群布置时，地面沉降最大值发生在腔群中心地表位置，在50年时达到了132.5 mm，是相同单腔开采条件下的6.66倍。由此可见，群腔开采对地面沉降的影响很大，因此需要对盐岩开采规模和腔群布置方式进行有效的控制。

3 结 论

1) 本文提出的预测模型所含未知参数较少，计算方便，在确定某工程的埋深及腔体形状的前提下，可以通过预估或者参考类似工程储库运行年份的腔体收敛情况，求得地表变形的动态过程。根据不同的腔群布置形式可以很方便的求解地表沉降分布，从而进行优化设计。

2) 通过和数值模拟的计算结果对比，本模型在变形动态预测和空间分布上具有较高的准确性，地表中心最大沉降值的动态预测差值最大为1.4 mm。当径向距离小于700 m时，地表变形的空间分布误差均小于10%。腔群开采的沉降计算表明，多腔储库建设对地表沉降的影响显著，所以在工程设计之初有必要针对腔群布置形式和建设规模进行进一步的研究和优化。

由于缺少实际监测资料，计算结果的准确性有待验证，同时本模型未考虑运行压力以及造腔过程的影响，这也必然导致计算结果与实际情况存在一定偏差。模型计算中的参数还需根据实际储库运行情况和腔体收敛结果进行进一步校核，以提高预测精度。