金融指数的单变点非参数极大似然估计研究

陈睿轩，田海涛，黄 磊

（西南交通大学 数学学院，成都 611756）

0 引言

变点问题的研究源于实际的需要。自1954年Page提出变点问题以来，变点问题经过长期的研究发展，已经应用于诸多领域。在金融计量经济学中，变点分析可以用于找出市场（或经济）的发展方向[1]，此外变点分析还能用于找出信用卡诈骗[2]和其他的异常情况。在信号处理方面，对一个图像流中重要变化的估计是十分重要的问题[3]。在医学上，变点问题在DNA的拷贝数变异检测上有了很大的应用，而在现代基因芯片技术所产生的海量数据中找出拷贝数的变异就是变点问题的一个最新的发展方向[4]。在数据挖掘中，变点问题也起着很重要的作用[5]。

近些年，越来越多的学者开始研究金融领域的变点问题[6-10]。然而，其研究内容都只局限于ARCH、GARCH等参数模型，很多时候金融市场数据往往不能很好地用参数模型去拟合，这时非参数的方法就应该被考虑到。本文的重点就是研究如何将非参数的变点方法应用到金融指数数据，并通过统计模拟实验和实际数据分析说明方法的可行性与实用性。

由于非参数方法不对数据所服从分布的结构提出任何的参数假设，其推断的有效性通常依靠渐进的证明，不同累积分布函数间有任何的差异，都将保证变点被渐进地探测出来。又由于非参数方法不对数据的分布做任何的假设，所以它可以灵活地适用于任何的分布。同时，单变点是变点问题研究中最为基础的问题，且单变点在实际处理数据中具有易操作性。因此，单变点非参数的估计方法是本文研究的重点。

对于金融领域的时间序列型数据而言，数据之间往往具有自相关性。在很多情况下，忽略自相关性而进行模型变点的估计，就会得到有偏差或者不相合的参数估计值，这将降低模型的预测能力，该问题可参见文献[11，12]关于非线性时间序列模型的研究。因此本文提出一个简单易行的方法，使得单变点非参数估计方法能适用于具有自相关性的金融时间序列数据。

本文中所考虑的金融时间序列数据为上证综合指数。上证综合指数从总体上反映了上海证券交易所上市股票价格的变动情况，也反映了当前中国市场的状况。当市场的经济形式发生变化，上证综合指数也会发生相应的变化，对这种变化的研究是十分有意义的。由于上证综合指数数据不是一个独立同分布的数据，带有自相关性，因此不能直接使用非参数估计方法，需要做相应的改进。本文的方法能有效地找出上证综合指数中存在的变点，这可以对中国经济的研究起到辅助作用，特别是宏观经济调控效果以及经济周期的研究。

1 单变点非参数极大似然估计

1.1 单变点问题的定义

设X1,X2,…,Xn是随机变量的观测值，一般情况下，假定X1,X2,…,Xn相互独立。如果X1,…,Xr-1同分布于F，Xr,…,Xn同分布于G，且F≠G，其中r是未知的正整数(2≤r≤n)，称其为变点。而单变点问题要解决的就是如何有效地估计出r的正确位置。

对于参数方法，首先需要假设F、G属于一些已知的参数函数族。再采用最小二乘法或者极大似然法，并通过一个动态选择程序来确定变点。然而参数方法虽然简便，但是需要确保对F、G分布假设的准确性。当假设不正确时，其估计结果与真实结果往往会有很大的偏差，而实际生活中，通常很难得知数据所属的真实分布。由于参数方法在实际问题中的局限性很大，所以大多时候都采用不需要考虑数据所属分布的非参数方法。

1.2 非参数极大似然方法

本文的方法是基于Zou等（2014）[13]所提出的非参数极大似然估计方法并对其进行改进，然后将改进后的方法应用于单变点问题。这样做的目的有两点：第一，对于金融时间序列型数据，数据量往往不大，比如研究股票日收益率，观测时间长度T取值过大会导致不同区间的异方差性，参见文献[14]。因此，在这种情况下，用传统的图形技术就能轻易地探测出变点。而且，对于中等或较小的数据样本，多变点模型会导致过度拟合；第二，对于确实需要进行多变点研究的数据，单变点方法可以通过迭代推广成多变点方法。因此本文主要研究单变点非参数极大似然估计，以及其对自相关金融时间序列数据的改进。

假设Z1,…,Zn独立同分布于F0，并让表示该样本的经验累积分布函数，则有，其中将其看作是有着成功概率(u)的二元数据的样本时，则可以得到非参数极大对数似然函数：

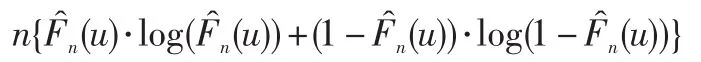
对于单变点问题，由于它是有两段独立同分布的数据序列拼接而成的，因此可以得到它的联合对数似然函数(Kn=1)：

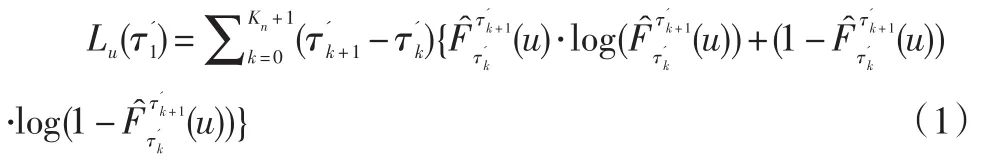
为了估计变点1＜≤n，在一个积分的形式下将式（1）最大化，得到：

其中，ω(·)是一些正的权重函数，所以Rn(·)是有限的，这个积分可以用来结合所有u的信息。

它是随着θ→q1，从两边逼近于的，且在q1点处具有极大值。

其中：

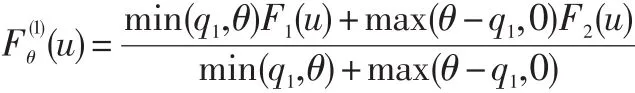
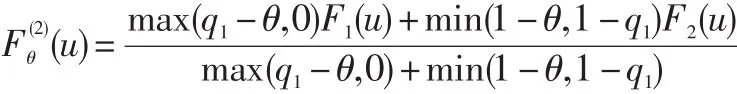
1.3 参数选择

本文所采用的极大对数似然方法的一个重要特性是可分离性，因此把任意点看作变点时，它都可以通过动态规划运算来计算出一个似然值，并把似然值最大的那个点当作估计变点，其总共的计算复杂度为O(n2)（参见文献[15，16]的动态规划运算的伪代码）。Hawkings（2001）[15]建议在一个m≪n值的坐标格中使用动态规划运算。Harchaoui和 Levy-Leduc（2010）[17]提出使用一个LASSO型罚参数的评估值来达到最小二乘法的一个简化版本。

在实际应用时，本文采用Zou等（2014）[13]提出的：

它被认为比dω(u)=(u)更有效。

当u∈(-∞,X(1))和u∈(X(n),∞)时（其中：X(1)＜…＜X(n)表示次序统计量），Lu=0，则式（2）可以改写成：

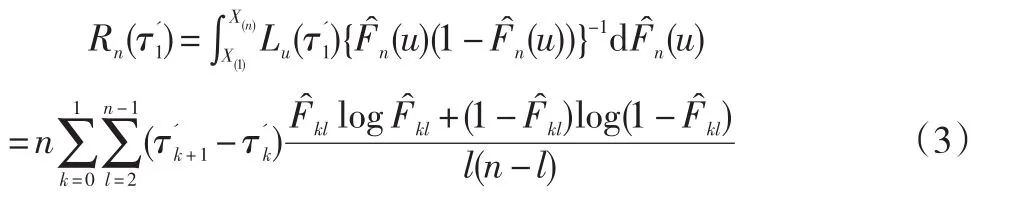
同时，本文使用施瓦茨-贝叶斯信息准则（BIC）来判断变点是否存在。如果存在变点，L=1；如果不存在变点，则L=0。

BIC准则是主观贝叶斯派归纳理论的重要组成部分，是最简单也是最典型的贝叶斯变量选择的方法。在信息不完全的情况下，本文采用主观概率来估计那些未知的状态，然后通过贝叶斯公式对所得概率进行修正，最后再利用期望值和修正概率来做出最优决策。因此，本文通过最小化BICL来确定L的值：

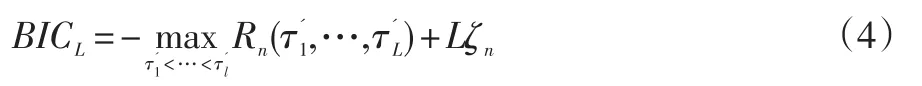
并且ζn是一个趋于无穷大的序列。

Yao（1988）[18]使用ζn=logn的BIC来选择变点的数量，并在最小二乘法的框架下显示出了它的连贯性，因此本文直接使用这个结果。

2 统计模拟

本文将通过模拟研究来测试非参数方法的一致性和有效性。在模拟研究中，本文将随机生成独立的数据序列和经典的时间序列。由式（3）和式（4）编写的程序将会应用于探测变点。

2.1 改进程序1

在模拟研究中，本文发现该方法对于变点存在性的判别不够准确。当模拟的数据序列中不存在变点，有时该方法却判断出：数据序列的前端或尾部存在估计变点。经过对数据序列的分析后，本文发现该方法在数据序列两端出现极端值点时易将该极端值点视为变点，形成误判。所以将该方法加以改进，当估计变点出现在两端2.5%处的数据量范围内时，判断该段数据序列不存在变点，该改进方法对应的程序称为改进程序1。当样本量特别小（小于1000）时，把比例从2.5%提高到5%才能较为有效地减少误判变点的发生。同时，采用ζn=(logn)2+c2,(c=0.1),将更为有效[13]。

2.2 改进程序1的独立数据的模拟结果

表1记录了在不同分布和样本量的情况下，变点估计的均方误差。在模拟研究中，估计的是θ。样本量N分别为100、200、400，相应的把真实变点设为51、101、201。所以相应的变点分位数θ为0.51、0.505、0.5025。令估计变点的分位数为q1，则均方误差其中，n是模拟的次数，本文中n=200。

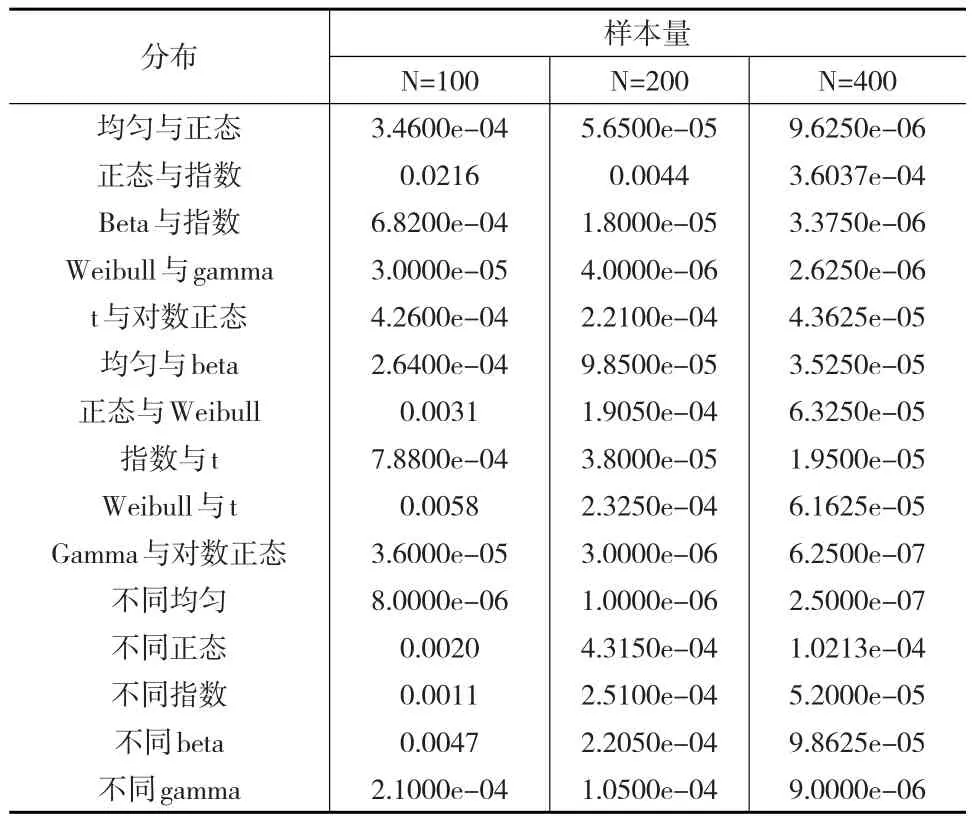
表1 变点估计的均方误差统计结果

由表1可以看出，改进程序1用于对常用分布组合的变点估计的准确度很高，且随着样本量的增大，对变点分位数估计的精度越来越高。因此，对于大多数独立数据序列变点的探测，改进程序1将会给出一个可信的结果。

2.3 金融时间序列上的应用

变点问题在时间序列上一直有着广泛的应用，也经常需要判断时间序列中是否存在变点以及变点的位置。但由于金融时间序列数据往往具有自相关性，而该非参数极大似然的方法要求每段数据序列是独立同分布的，因此，该非参数方法需要一些改进。

本文使用平稳的ARMA模型生成时间序列的随机数据。自回归滑动平均模型（Auto-Regressive and Moving Average Model,ARMA模型）是研究时间序列的重要方法，也是研究平稳随机过程有理谱的典型方法，适用于很大一类实际问题。

ARMA模型分为以下三种：自回归模型（Auto-Regressive,AR模型）、移动平均模型-（Moving-Average,MA模型）、自回归滑动平均模型（ARMA模型）。

在模拟研究中，本文采用AR模型来生成时间序列的随机数据，之后尝试直接使用改进程序1进行变点的估计。结果显示，直接使用改进程序1来估计变点有着很大的偏差。所以本文决定对数据序列进行预处理来减少数据间的相关性，采用差分的方法来对原始时间序列数据做预处理并得到一个新的数据序列。把加入预处理的程序称为改进程序2，模拟结果记录在表2中。

表2 两种改进程序对时间序列变点估计的均方误差结果比较

表2记录了两种改进程序的变点估计的结果。表2的结构与表1相同，且样本的模拟次数n=200。

从表2中可以看出，对于时间序列，改进程序2比改进程序1有着更好的估计结果。改进程序2变点估计的均方误差更小，估计更准确，也更令人满意。因此，本文认为，非参数极大似然方法不能直接用于时间序列的变点估计，但是在做差分的预处理后，该方法是可行的。虽然在一些情况下，估计结果不如独立同分布的数据序列的估计结果好，但是仍然可以接受。对于复杂的时间序列，估计的偏差总是存在，这可能是因为对于复杂的时间序列，差分的预处理并不足以有效地消除数据间的相关性。如果有更为有效的预处理方法，那么非参数极大似然方法仍是有效的，这也将是下一步的研究方向。

3 金融指数实证分析

上证综合指数反映了上海证券交易所上市股票价格的变动情况，是分析整个市场状况的一个良好数据。本文对2015年4月7日至2017年4月6日的上证综合指数（共463个数据）进行分析。由于是金融类的时间序列数据，所以预处理采用log差分，即采用Rt=log(Yt)-log(Yt-1)，得到回报波动率进行考虑。对log差分后的数据Rt进行自相关分析（见图1）。

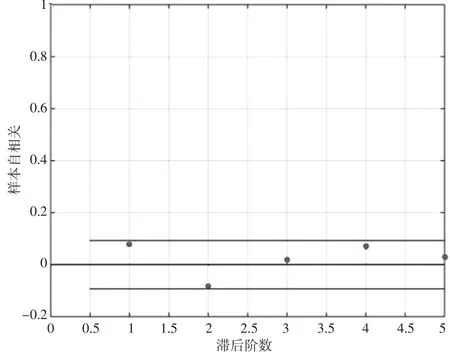
图1 Rt样本自相关函数

从图1可以看出，log差分后的数据Rt在5阶内可以认为相关性不显著，说明用log差分代替差分作为预处理手段是可行的。之后对Rt进行变点的判别。结果如图2所示。

图2 各变点似然函数值

从图2可以看出，最大值点为228。由于序列中的第1个点是不能作为变点的，所以本文从第2个点开始判断，图中显示的变点228实际上指的是Rt中的第229个点。本文以变点229为分界绘制Rt的数据，情况如图3所示。

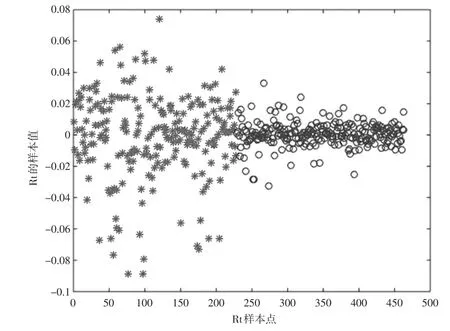
图3 Rt样本的数据分布

从图3可以看出，以变点229分割后的两段Rt数据分布有着明显的不同：第一段数据序列的波动性更大，第二段的数据序列更为稳定。而Rt数据序列的变点229对应的是2016年3月31日。此结果与市场的反馈是一致的。

采购经理指数（PMI：Purchase Management Index）是一套月度发布的、综合性的经济监测指标体系。PMI有着及时性与先导性、综合性与指导性、真实性与可靠性、科学性与合理性、简单易行五大特点。PMI是经济回暖的先行指数，对于经济预测和商业分析方面都有着重要的意义。

通过国家统计局公布的数据绘制图4。

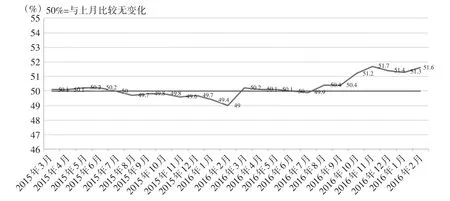
图4 制造业PMI指数（经季节调整）

从图4可知，2016年3月前的PMI数据大多在50%以下，表现出国内经济状态的低迷。而在2016年3月，中国制造业PMI为50.2%，比上月上升1.2个百分点，重回扩张区间。并且从该点开始，其后的PMI数据大多在50%以上，这显示国内经济形势变好。这与之前的低迷状况不相同，说明这两段时期的经济状况所属分布是不同的。这证明了非参数极大似然方法所找出的变点：2016年3月31日是和市场经济的宏观调控结果一致的，也说明了该方法在实际应用中是可行的。

4 结论

变点问题是当前的热门问题之一，本文采用一种非参数极大似然方法来解决单变点问题。该非参数极大似然方法对于独立数据序列的变点判别有着很高的精度。再加入差分作为预处理手段后，该方法对于金融时间序列数据也有着很好的效果。统计模拟显示，本文所提出的改进方法将会获得更加一致的估计结果，改进后的非参数极大似然方法在实际数据分析中也是可行的。通过对2015年4月7日至2017年4月6日的上证综合指数的变点分析，发现估计变点的结果与实际PMI指数的变化是吻合的。变点估计显示上证综合指数在2016年3月31日存在变点，市场在此前后的状态是不同的。而实际PMI指数显示，市场在2016年3月后经济形式脱离低迷状态，重回增长状态。由此可见，本文所提出的方法在实际应用中的效果明显，同时也说明对于自相关的金融时间序列数据，预处理的改进措施是必要的。改进后的非参数极大似然方法可以做进一步拓展使其适用于其他情形，如多元的情况。这些后续的问题仍需要进一步的研究分析。