基于非线性多基站分布式混沌随机共振方法的无线通信系统定位技术研究

何 迪，张 毅，郁文贤

(1.上海市北斗导航与位置服务重点实验室，上海交通大学，上海 200240；2.华为技术有限公司，上海 200135；3.上海市智能探测与识别重点实验室，上海交通大学，上海 200240)

0 引言

近几年来，随着不同类型终端用户对高精度定位的需求日益增加，对高精度定位技术的研究也呈现爆发之势。例如，以高精度载波相位差分(Real-Time Kinematic，RTK)技术为基础的全球导航卫星系统(Global Navigation Satellite System，GNSS)[1-3]、多源/全源融合定位技术[4-6]、同时定位与制图技术(Simultaneous Localization and Mapping，SLAM)[7-9]等新兴技术的研究都受到了广泛的关注。而在这些新兴的高精度定位技术方法中，绝大部分都需要添加额外的基础设施或者较为复杂的传感器或多种传感器的组合以实现最终的高精度定位需求，同时这也大大增加了上述定位方法实施的难度。而对于无线定位方法来说，无线通信系统自身的基础设施(如室外环境中的无线基站以及室内环境中的WiFi等)已经较为完备，一般来说已经不需要再单独架设其他的定位设施，这就给无线定位带来了非常大的优势。不过，传统无线定位方法的定位精度在一些复杂环境(如高架路、城市森林、隧道、湖泊等)以及低信噪比环境下的定位精度较差，仍需要进一步的改进和完善。

当前已有的一些研究成果表明，如果希望在复杂的无线传输环境中最终获得较理想的定位精度，可以考虑采取高精度的信号到达角估计方法[10]、高精度的信号到达时间[11]或信号到达时间差估计方法[12]，以及以上两种参数估计的组合或者融合方式[13]来实现。对于基于信号到达时间的定位方法来说，需要整个无线定位网络保持高精度的时间同步[14]，而这一点要在实际的无线通信网络中实现是非常困难的。对于基于信号到达角估计的定位方法而言，无线信号在实际传输环境中所遇到的多径问题和非直射径问题成为了影响定位精度的主要障碍[15]。特别是在无法判定所接收到的信号是否为直射路径信号的情况下，往往会使得传统基于信号到达角估计的定位方法产生较大偏差甚至失效。基于上述原因，非常有必要深入研究更为有效的无线定位方法来克服上述问题。

在本研究工作中，新提出了一种无线定位的机制和方法，其主要原理是引入了一种基于非线性混沌随机共振的动力学方法，并与分布式多基站信号处理相结合，从而有效改善上述问题。混沌随机共振是一种在非线性系统中的信号处理方法，用于描述非线性混沌系统中内部噪声或外在噪声的存在可以增强系统输出响应的一种特殊现象[16]。在信号分析过程中，噪声通常被认为是使系统性能恶化的原因之一，因为噪声的存在降低了信噪比，影响了有用信息的提取。然而在某些特定的非线性系统中(如非线性混沌随机共振系统)，噪声的存在能够增强微弱信号的检测能力，这种现象就称为混沌随机共振[16]。在本文中，通过所引入的非线性混沌随机共振信号与处理分析方法以及分布式的混沌随机共振信号处理结构，可以在满足一定条件的情况下改善接收信号的功率谱特性，从而在一定程度上抵抗甚至抵消由无线信号传输中所产生的路径衰落、多径干扰或其他信号/用户干扰等。同时，通过采用分布式多基站信号功率谱融合的方法，前述的无线接收信号非直射路径所带来的问题也可以在很大程度上得到缓解。通过计算机仿真分析表明，采用所提出的这种无线通信系统定位方法，即使在较低的信噪比和非直射路径情况下，仍然能够得到较高的定位精度，这也从实验的角度进一步验证了所提出方法的可行性和有效性。

本论文的主体结构如下：引言是对论文研究工作和研究背景的总体概括性介绍；第1节中针对传统无线系统定位方法的特性进行了简要的讨论，特别是对这些方法在低信噪比和非直射路径下的局限性进行了描述；第2节详细介绍了所提出的基于非线性混沌随机共振的分布式无线通信系统功率谱融合定位方法；第3节给出了相应的计算机仿真分析结果，并与一些传统的无线定位方法进行了性能比较；最后在第4节中对全文进行了归纳和总结。

1 传统无线定位方法的特性

无线通信系统的定位在各类定位系统中是一种比较特殊的结构。由于它具有与公共无线通信网络天然的互通性，使得其能够与公共无线通信系统的发展紧密结合。特别是在当前的室内WiFi通信系统广域覆盖、室外4G无线通信系统蓬勃发展、未来的5G无线通信系统方兴未艾之际，对无线通信系统的定位进行深入研究，一方面具有重要的现实意义，另一方面也能够适应广大无线终端用户未来快速发展的迫切需求。相信随着今后一段时间物联网技术、工业4.0、智能制造等的不断创新，无线通信系统的定位必将会在不同领域发挥越来越重要的作用。

在无线通信系统和无线定位系统中，无线信号的传输一般都遵从特定的传播特性和传播规律。例如，假设发端只包含有单个信号源时，远场的接收信号可以表示为：

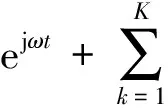
ejω(t-τk)+n(t)

(1)

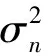
在传统的无线定位方法中，如果要实现高精度的测角结果，一般可以在接收端采用阵列信号处理的方法来实现，如经典的MUSIC方法或ESPRIT方法等。在这类方法中，通过在接收端设置不同结构的接收天线阵列，同时设置接收阵列中接收阵元的间距和排列结构，使得不同接收阵元上的接收信号具有一定的差异性。当该差异性能够反映出接收信号的到达角信息时，即可通过一定的阵列信号处理方法来实现对信号到达角的估计。其中，由于基本的ESPRIT方法只适用于等距线阵，因此其适用场景和适用范围受到一定的限制。而MUSIC方法由于不受到此限制，而且可以在三维空间场景中使用(即可以同时估计信号的方位角和俯仰角)，成为基于阵列信号处理的到达角估计方法中的主流。

即便如此，在以上所述的方法中，仍然存在一个非常实际的现实问题难以解决。当接收端所接收到的信号的直射信号分量被部分或完全遮挡的情况下，以上的这些方法实际上无法判断所接收到的信号是否包含有直射信号分量。在此情况下，这些方法都只能够根据接收信号的方向能量来直接分析，或相应地将接收信号能量最集中的方向判断为信号的到达角方向。因此，如前所述，当直射信号分量被遮挡或者衰落很严重时，依据这些方法所估计得到的到达角会产生严重偏差，并最终导致无线定位结果产生很大的定位误差。

2 基于多基站分布式混沌随机共振的无线通信系统定位方法

为了缓解第1节中所描述的无线定位中经常会出现的这个问题，在本研究中提出了一种基于分布式混沌随机共振技术的功率谱融合无线定位方法，并在下面具体地讨论该方法的有效性与可行性。

如前所述，当直接采用传统的基于接收端阵列信号处理的方法来实现信号到达角估计时，实际上无法判断接收信号的直射路径是否仍然具有最强的功率。但与此同时，诸如MUSIC或ESPRIT等这类阵列信号处理的方法不仅能够用来直接估计信号的到达角，还可以用来估计接收信号的功率谱信息。基于无线通信信道中的噪声信号统计特性，功率谱信息实际上反映的是在各个可能的波达方向上入射信号功率的概率密度或概率分布。换而言之，如式(1)中所见,接收信号中所包含的直射信号分量、多径信号分量以及噪声信号分量等的所有信号分量的功率谱信息都能够反映在阵列信号的功率谱信息当中。而对于多用户的无线移动通信系统来说，用户之间可以通过不同的多址方式在基站侧来进行有效的区分，如传统的频分多址方式、时分多址方式，到目前系统中较为常用的码分多址方式、空分多址方式，以及未来可能使用的包分多址方式和目前仍然停留在理论层面的极分多址方式等。在对不同用户的信号进行有效区分之后，即可进一步实现本文中所提出的无线定位方法。

与此同时，一般都可以假设在信号接收端已知发端信号的一些基本信息，如信号的调制方式、载波信号的频率等。无线通信或无线定位的信号一般都采用正弦波作为高频载波信号。这样，从信号模型的角度来进行分析，当接收信号的直射分量衰落较为严重时，其接收信号的振幅也就相应地会产生较大的衰落，甚至会淹没在多径信号或噪声信号的功率谱中。

基于此，可以首先考虑采用非线性系统中的混沌随机共振方法来对接收信号中的直射信号分量进行混沌随机共振处理[16]。其信号处理模型如下：

(2)

在非线性混沌随机共振系统中，当共振系统f[·]、状态变量xCSR(t)、外部输入激励信号e(t)和共振噪声信号nCSR(t)满足一定的共振条件时，状态变量xCSR(t)将会呈现出与外部输入激励信号e(t)相类似的时频域特征。特别是当外部输入激励信号e(t)为直流激励信号或者单一频率的低频信号时，该特性越发明显[17-18]。具体的系统共振特性与系统响应特性与多个因素有关，包括所选择的非线性混沌随机共振系统、输入激励信号的时频特性、共振噪声信号的时频特性等。

以经典的双稳态混沌随机共振系统为例，其状态方程如下所示[16]：

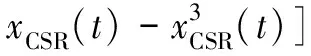
d1·e(t)+d2·nCSR(t)

(3)

其中，xCSR(t)为系统的状态变量，g、h、d1和d2为系统的特定参数，Δt为系统的采样间隔，nCSR(t)为系统的共振噪声。

根据随机共振系统中的线性响应理论[16]，当激励信号e(t)和共振噪声nCSR(t)相互独立时，系统的状态变量可分解为：

xCSR(t)=eres(t)+nres(t)

(4)

其中，eres(t)为对应于激励信号e(t)所产生的系统响应量，nres(t)为对应于共振噪声nCSR(t)所产生的系统响应量，以上两者满足线性叠加关系。

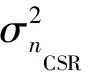
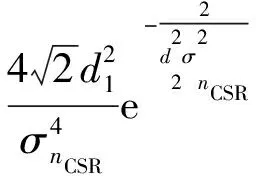
(5)

对于外部输入激励信号e(t)来说，在一般的无线通信系统中，特别是针对某个单一的收/发用户通信信号体制而言，都能够满足其载波为单一频率的正弦信号这一条件。因此，在实际应用中，一般可以通过以下方式来实现：对接收信号进行相干解调时，在载波信号的角频率ω上叠加一个很小的角频率偏差量Δω，以使得解调后的信号具有较低的载波频率，以保证混沌随机共振的效果能够较好地显现出来。

基于以上的考虑，将所接收到的信号振幅作为混沌随机共振系统的外部输入激励信号e(t)，即：

(6)

(7)

将上面混沌随机共振系统模型中激励信号的信噪比表示为SNRin，而将状态变量xCSR(t)中对应激励信号频带内的频谱分量作为整个系统的输出信号，且输出信号的信噪比表示为SNRout。根据随机共振系统的线性响应定理与功率谱增益定理可得，在满足一定条件下(如激励信号的信噪比较低，如低于-10dB，同时激励信号是一个单一频率的正弦信号或窄带信号)[16]，输出状态变量的信噪比相对于激励信号的信噪比能够产生一定的增益，即:

SNRgain=SNRout-SNRin>0

(8)

在这里，SNRgain即为激励信号通过混沌随机共振系统之后所得到的信噪比增益。可以看到，该信噪比增益显然会对提升传统的无线定位方法的定位性能起到重要而积极的作用。

与此同时，虽然说混沌随机共振系统具有以上的信噪比提升特性，但是其特性的提升一般是随着信号采样点数的增加而呈现单调非递减关系的。换句话来说，如果要获得较为理想的信噪比增益结果，则有可能需要较多的采样点数或较长的采样时间来实现，这也是该方法在实际应用中的一个缺陷。

为了进一步地克服上述困难，这里借鉴一种非线性分布式混沌随机共振系统来解决这一问题。图1给出了本文研究所提出的共振信号处理框架，图2则表示了在每个接收阵列处的分布式混沌随机共振信号处理框架结构，图2的结构对应于图1中间一行并行处理的分布式混沌随机共振信号处理模块的具体信号处理结构。由图1可以看出，每个基站或接收阵列在接收到信号r(t)之后，首先进行式(6)所示的取模运算。之后，在每个基站或接收阵列处分别进行分布式混沌随机共振处理，并得出处理之后图2中在每个接收阵元处的输出信号xCSR-m(t)，其中m=1,2,…,M，而M假设为每个接收阵列中所包含的阵元个数。对每个基站或接收阵列中的所有接收阵元的输出信号xCSR-m(t)求取平均值，得到:

(9)

图1 非线性分布式混沌随机共振系统框架Fig.1 Block diagram of the nonlinear distributed chaotic stochastic resonance system

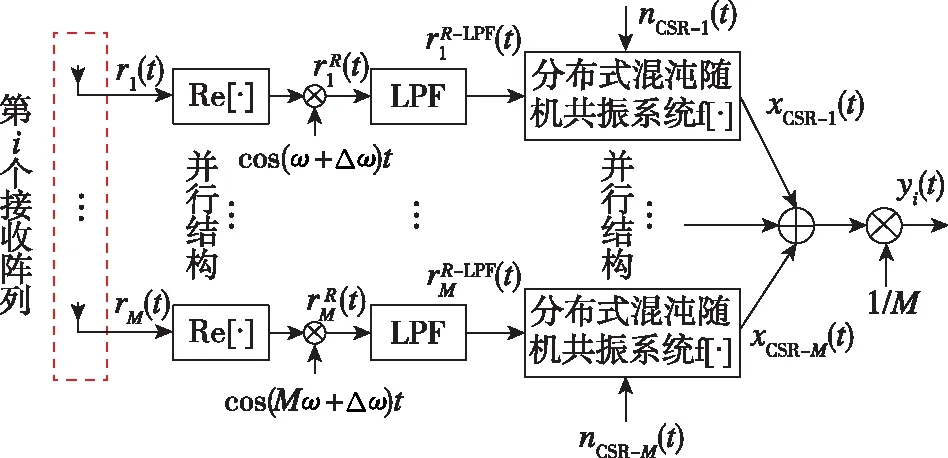
图2 在每个接收阵列处的分布式混沌随机共振信号处理框架结构Fig.2 Distributed chaotic stochastic resonance signal processing structure at each receiving array

以上所述方法即为一种最为简单的分布式混沌随机共振信号处理方法。在这种处理方法中，通过在任意一个基站或接收阵列上的每一个接收阵元通道上分别进行并行分布式混沌随机共振处理，再将各接收阵元通道上的输出结果xCSR-m(t)进行合并。文献[19]的研究结果已经清楚地表明，当将式(7)中的集中式混沌随机共振处理的总采样点数平均分配到各个接收阵元通道上去进行并行分布式混沌随机共振处理后，可以得到更好的信号信噪比增益。换句话说，假设式(9)中信号yi(t)的信噪比为SNRDCSR-out，其相对于SNRin的信噪比增益为SNRDCSR-gain，则有

SNRDCSR-out>SNRout>SNRin

(10)

SNRDCSR-gain>SNRgain>0

(11)

按照以上的方法，当把每个接收阵列上的信号功率谱进行分布式计算之后，再将这些所有的分布式功率谱集中起来进行功率谱数据融合。这里，可以考虑采用以下两种比较简单的融合方式：一种是加权求和式融合，即：

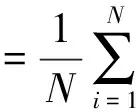
(12)

其中，βi表示第i个接收阵列所对应的加权权值，有：

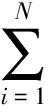
(13)

或者采用以下的乘积式融合方法：

(14)

在式(12)和式(14)中的等式左边，Ptotal(θ,φ)即为融合之后的信号功率谱。

如前所述，由于每一个接收阵列处所产生的信号功率谱不仅包含直射信号分量的功率信息，而且理论上还包含所有的多径信号的功率信息。因此，在融合的过程中，即使有某一个或某几个基站或接收阵列所接收到的直射信号分量衰落较为严重甚至完全被遮挡，通过其他几个基站或接收阵列上的功率谱信息仍然能够在一定程度上克服传统方法在这一问题上的缺陷。同时，由于在不同基站或接收阵列上所对应的多径信号分量一般会有很小的概率处于相同的波达方向上。因此，它们在某一个基站或接收阵列上较高的波达方向功率谱一般反而会在功率谱融合的过程中被平均掉或被削弱，总体上进一步降低了多径信号对波达方向估计的影响。所以，本研究所提出方法的优越性可以得到进一步体现。

3 计算机仿真分析与性能比较

在本节中，对所提出的无线定位方法进行计算机仿真以验证其性能，并将其与一些传统的无线定位方法进行性能上的比较。

在下面的仿真过程中，为简化仿真和计算，做如下的参数假设和选取：设置发射信号的振幅(包络)为常数，载波信号的角频率为ω=5×108rad/s，角频率偏差量为Δω=0.2rad/s；接收端的多径数设为2；假设针对待检测的接收机，有4个基站可以接收到所发射的信号，并可用于进行相关的分布式混沌随机共振处理和功率谱融合。在4个基站中，假设有1～2个基站与发射机之间的直射信号分量被遮挡，且每个基站上放置一个16阵元的均匀圆阵用于进行阵列信号处理。4个基站的坐标位置为(0,0,0)、 (30,0,0)、(0,30,0)和(30,30,30)，接收机的坐标位置为(21.5,23.1,29)，上述坐标的单位都为m，且接收端有2条随机产生的多径信号。融合时采用加权求和式融合方法，且假设每个接收阵列所对应的加权权值都相等。

在进行混沌随机共振处理时，采用经典的双稳态混沌随机共振系统，其状态方程如式(3)所示。在计算机仿真中，以上参数选取为经典的双稳态混沌随机共振系统参数，即g=2.85、h=10，nCSR(t)选取为均值为0、方差为1的高斯白噪声，而参数d1和d2的值可由系统的优化过程来确定[16]。

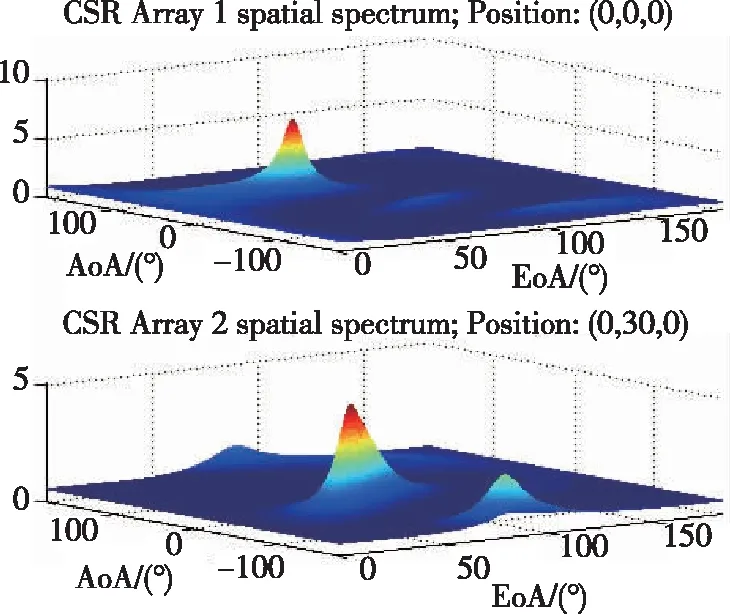
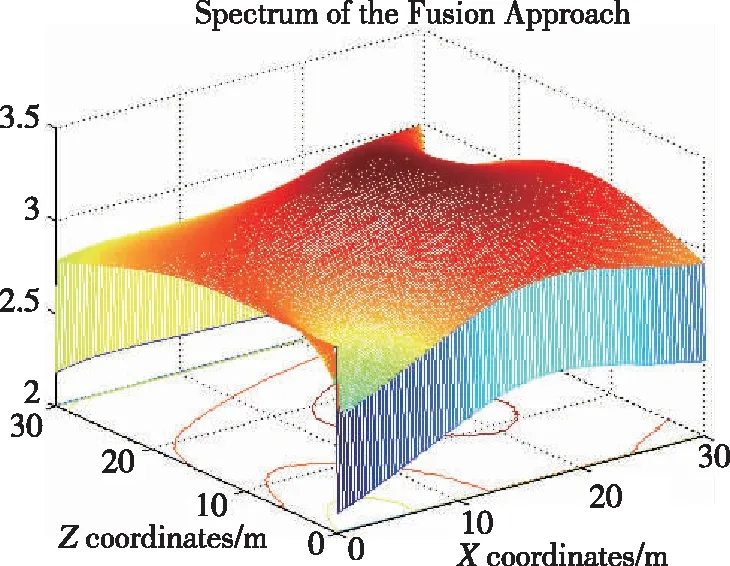
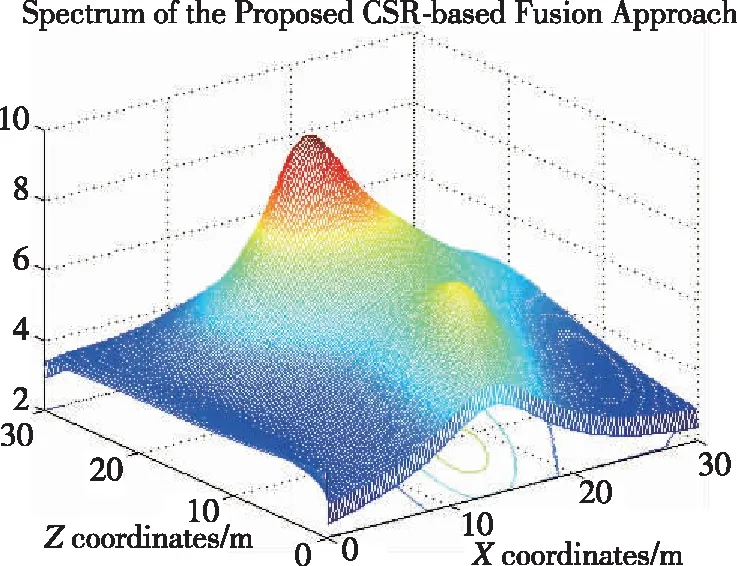
图3所示为在接收信号信噪比为-10dB的条件下，4个基站接收阵列处混沌随机共振增强前与混沌随机共振增强后所对应的信号空间谱对比结果。从图中可以很明显地看到，在目标位置处的信号空间谱尖峰经过混沌随机共振增强之后更加突出，而且还具有一定的降噪功能。图4给出了在接收信号信噪比为-10dB的条件下，普通融合方法与所提出的基于混沌随机共振增强谱融合方法的信号空间谱对比结果。同样可以看到，经过融合之后，从信号空间谱特性中能够更加准确地反映并且估计出信号到达角的参数，为增强无线定位的性能奠定了良好的基础。

接下来，图5给出了在不同信噪比条件下的信号到达角估计误差RMSE的性能对比结果，其中对比了传统的MUSIC算法到达角估计结果、未经过混沌随机共振处理之前的功率谱融合到达角估计结果，以及本文所提出的经过混沌随机共振处理之后的功率谱融合到达角估计结果。从结果中可以看到：首先，未经过混沌随机共振处理之前的功率谱融合结果已经能够较好地改善传统方法的信号到达角估计性能；而经过混沌随机共振处理以及功率谱融合之后，其性能又可以得到再进一步的改善。最后，图6的仿真结果给出了不同信噪比条件下以上各种方法的定位估计误差RMSE性能对比结果，该结果也同样反映了所提出方法对定位结果性能的有效改善。尤其是在低信噪比条件下，由于非线性混沌随机共振对接收信号信噪比的提升，使得其定位性能的改善更加明显。从图5和图6的仿真结果中也可以定量地看到，在低信噪比条件下的定位性能改善效果更加明显。如在信噪比为-6dB的情况下，无论是到达角估计结果还是定位估计结果，所提出的方法都比传统方法改善了3dB以上的性能。

(b)

(c)

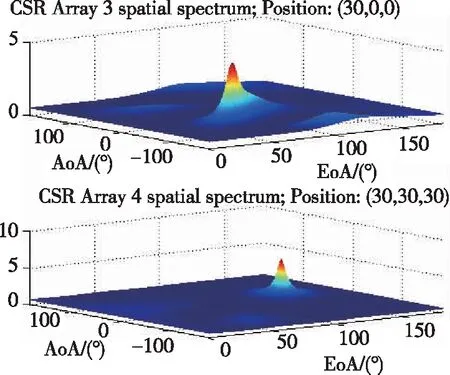
(d)图3 在接收信号信噪比为-10dB条件下每个接收阵列处混沌随机共振增强前与混沌随机共振增强后所对应的信号空间谱对比结果Fig.3 Spectrum comparison result before and after chaotic stochastic resonance improvement at each receiving array with SNR=-10dB

(a)

(b)

(c)

(d)图4 在接收信号信噪比为-10dB条件下的普通融合方法与所提出的基于混沌随机共振增强谱融合方法的信号空间谱对比结果Fig.4 Spectrum comparison result of general fusion method and proposed fusion method based on chaotic stochastic resonance with SNR=-10dB

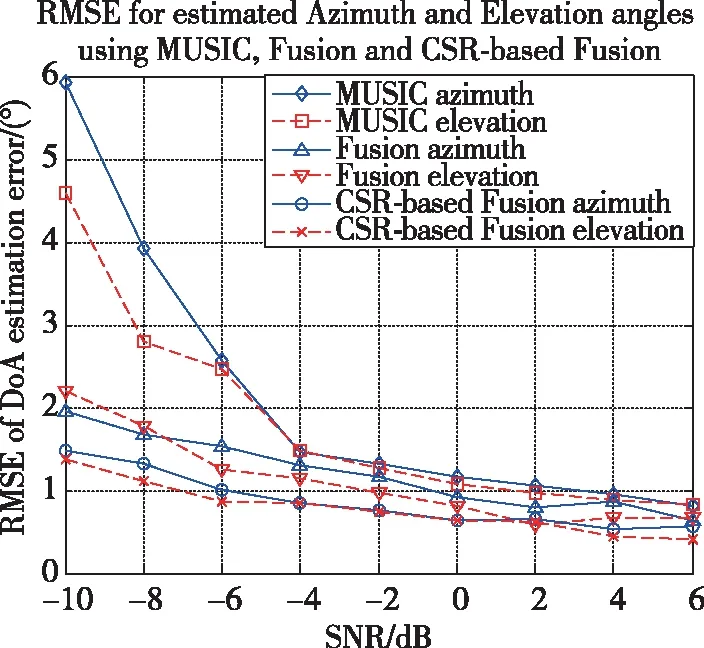
图5 不同信噪比条件下的信号到达角估计误差RMSE性能对比结果Fig.5 RMSE performance comparison results of DOA estimation error under different SNR conditions

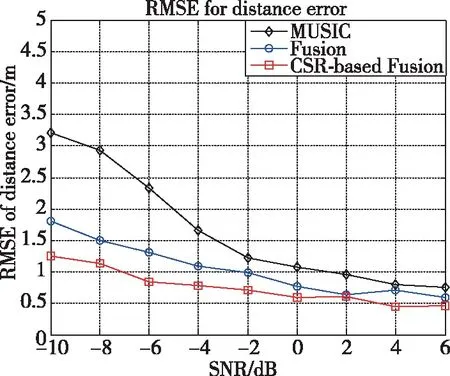
图6 不同信噪比条件下的定位估计误差RMSE性能对比结果Fig.6 RMSE performance comparison results of positioning estimation error under different SNR conditions

4 结论

在该研究中，针对传统无线定位方法所遇到的困难和问题，本论文提出了一种基于非线性多基站分布式混沌随机共振方法的无线定位技术。其主要创新点和特性可归纳如下：

1)利用非线性混沌随机共振动力学系统在特定条件下对激励信号的增益作用，以及将分布式随机共振系统与通信系统中的功率谱融合相结合的特点，实现了对非直达波信号到达角的有效估计。

2)所提出的方法可以较为有效地解决无线定位系统中常见的多径问题和非直射径问题。

3)实验仿真分析也充分证明了所提出方法的优越性，如在信噪比为-6dB情况下，无论是到达角估计结果还是定位估计结果，所提出的方法都比传统方法改善了3dB以上的性能。这也对其在实际系统中的应用奠定了基础。