两种不同方法下的矿井涌水量预测对比分析∗

褚双燕，王中美，王亚维

(贵州大学 资源与环境工程学院，贵州 贵阳550025)

0 引言

我国矿区水文地质条件非常复杂、防治水害任务异常艰巨，因此，对于矿井防治水技术研究不断探索，方法也在不断的发展改进.矿井涌水量是评价矿井开发经济技术条件的重要指标之一，同时也是制定矿山排水设计、选取开采方案及制定防治疏干措施的主要依据，矿井涌水量的预测将直接影响到矿山的生产安全和工程建设及采矿成本[1−3].目前，常用方法有水文地质比拟法、地下水动力学解析法、水均衡法、人工神经网络法等[1−11].这些方法对水文地质参数的依赖性强，而在岩溶区矿山内，含水介质的各向异性、非均质性特别突出，水文地质参数很难获取，故无法对矿井涌水量开展可靠性预测.近几年，有些学者采用人工神经网络法预测矿井涌水量，但是该方法在实际的勘查和生产中很少应用[12].相关分析法可适用观测资料较全的、开采多年的矿井，对于水文地质参数不确定性所引起的预测误差能够最大程度降低，弥补了水文地质勘查程度不高或参数缺乏的不足，提高预测可靠度.灰色系统是邓聚龙教授在1982年提出的概念，目的在于解决所获取的资料信息不确定性问题.在该系统下建立的模型弱化了信息完全不明确的影响，是理想的含有不确定性的数据的预测模型.相关分析和灰色理论两种方法对水文地质参数的依赖性弱，甚至可以不考虑水文地质参数的相关因素.

1 研究区概况

研究区地处贵州省六盘水市水城县境内，属长江流域乌江水系，矿区四周均有地表河发育，见图1，年降雨量一般为1 261 mm.研究区地形总体中间高，四周低，地貌类型为侵蚀—溶蚀低中山沟谷.矿区位于小河边向斜南西翼，出露二叠系峨眉山玄武岩组、龙潭组、三叠系飞仙关组、永宁镇组及第四系地层，以走向北东、倾向南东的单斜构造为基本构造形态，见图2.研究区地下水类型主要为赋存于永宁镇组灰岩的岩溶裂隙水，赋存于峨眉山玄武岩组、龙潭组砂页岩、三叠系飞仙关组泥岩的基岩裂隙水及第四系孔隙水.大气降水为区内地下水的主要补给来源，以泉排泄方式于沟谷地带排入地表河流.矿区内含煤地层为二叠系龙潭组，主采煤层为08#、11#、13#三层煤，平均厚度一般在66∼78 m，可采煤层总厚度一般在20～31 m.采用走向长壁后退式开采方式，矿井设计能力为90万吨/年，实际产量为55万吨/年.

大气降水是矿床充水的主要因素.由于矿区开采历史悠久，小煤窑分布较多，矿区塌陷与采空区连成一体，地表裂隙较为发育，形成矿区的主要导水通道，主要体现在：矿井涌水量增加；老窑积水段对采掘生产造成很大威胁.因此为了煤矿的安全开采，矿区涌水量预测至为关键.

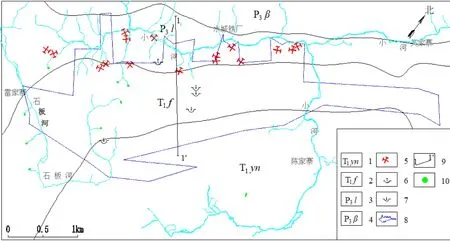
图1 研究区水文地质简图Fig 1 Hydrogeological Map of the Study Area

2 数据来源

本文采用的相关分析法和灰色理论，以老鹰山煤矿实测1995—2016年的降雨量资料和每年的气象资料整理得到的数据进行模型建立，并预测该矿区2014—2016年的矿井涌水量.相关分析法通过建立回归方程，用剩余标准差σ对模型的适用性进行检验，灰色理论应用GM(1,1)模型拟合涌水量进行预测.

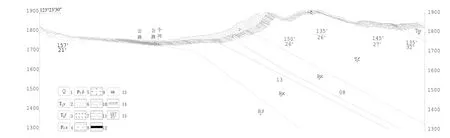
图2 研究区水文地质剖面图Fig 2 Hydrogeological Section of the Study Area

3 基于相关分析的矿井涌水量

3.1 相关分析的解析

矿井涌水量受多种因素的影响，这些因素间往往没有确定的函数关系，却存在着某种统计关系.本文应用相关分析法预测矿井涌水量，研究现象之间是否存在某种依存关系，并对具体有依存关系的现象探讨其相关方向以及相关程度，这种关系是非确定性关系.运用这种方法建立的关系模型的最大优点是：避开了水文地质参数非确定性影响；通过分析因变量与自变量关系，建立矿井涌水量统计预测模型[13−16].利用数理统计[17]相关系数分析矿井涌水量与相关因素的密切程度.

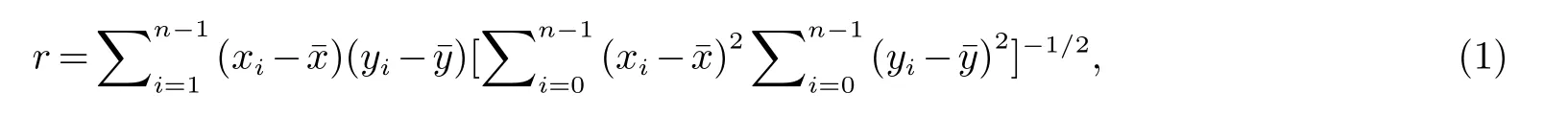
当相关系数r≥0.8时，矿井涌水量与影响因素密切相关，可建立线性相关公式.

3.2 相关程度分析

根据1995—2013年矿区多年降雨量及矿井涌水量资料，见图3.矿井涌水量与降雨量分析结果表明，老鹰山煤矿的矿井涌水量与降雨量的相关系数为0.835，检验概率值为0.00，见表1，故煤矿矿井涌水量与降雨量之间显著相关.

表1 矿井涌水量与相关因素降雨量的相关程度及显著性分析Tab 1 Correlation and Significance Analysis of Mine Water Inflow and Related Factors Rainfall

3.3 回归方程的建立

矿井涌水量与降雨量呈S形曲线相关，见图4.设矿井涌水量Q与累计降雨量X回归方程为

方程建立后还需要对预测结果的精度进一步分析.剩余标准差σ显示了各实测点偏离回归方程的程度，可表示回归方程外推预报的精准程度.

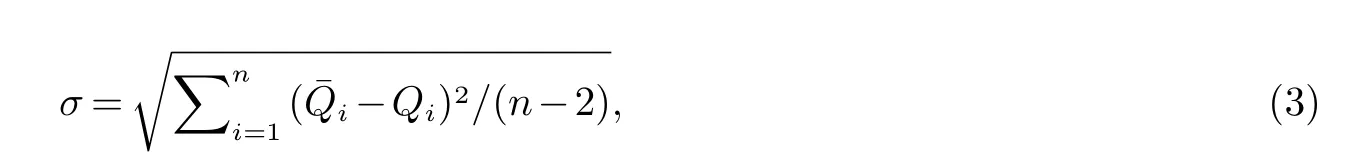
式中，σ为实际值与预测值的剩余标准差；为预测值；Qi为实际值.

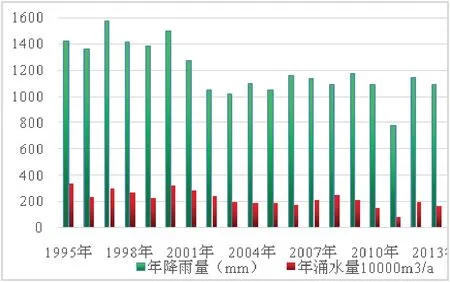
图3 1995年至2013年实际测得的降雨量与涌水量Fig 3 Actual Measured Rainfall and Water Inflow From 1995 to 2013

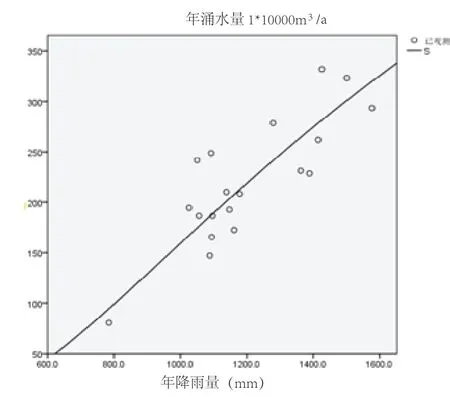
图4 矿井涌水量与降雨量散点图分布Fig 4 Distribution of Mine Water Inflow and Rainfall Scatter Plot

根据随机变量成正态分布的理论，将Q的观测值代入（3）式中.在回归方程中，87.19%的实际观测值都落在回归曲线两旁各一个剩余标准差的范围内，见图5.就是说任一实际值Qi落在（Q±σ）内的概率P为87.19%，可见，方程式预测的准确度较高.

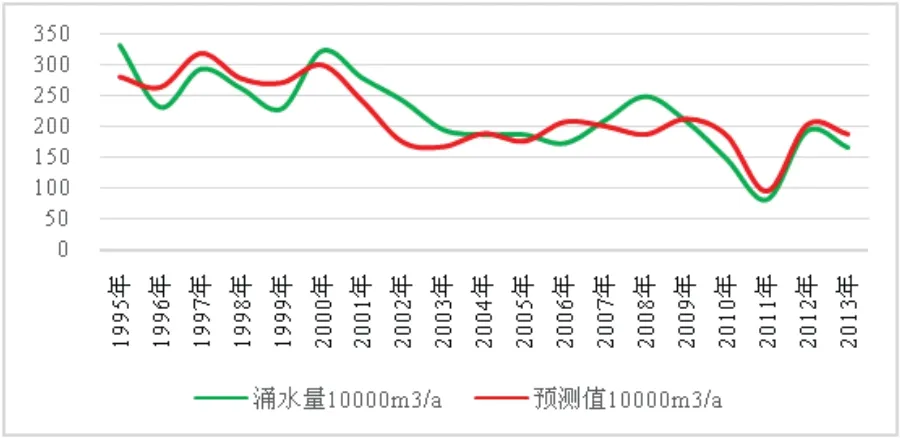
图5 老鹰山煤矿矿区涌水量预测结果-相关分析Fig 5 Prediction Results of Water Inflow in Laoyingshan Coal Mine Area-Correlation Analysis

表2 2014年至2016年实测值、预测值及误差Tab 2 Measured Value, Predicted Value and Error From 2014 to 2016

从表2预测结果可见，预测精度是呈上下浮动变化的，主要原因在于该模型为单变量预测模型，但是影响涌水量变化的因素较多，随着季节的变化，矿区内影响因素动态变化大，数据不稳定，是导致预测结果误差变化的一个重要的因素.

4 基于灰色系统理论的矿井涌水量预测

4.1 灰色理论基本原理

灰色理论基本原理是将离散的、随机的原始数据列进行累加处理，然后得到规律性强的累加生成序列，建模后，反推累减还原为预测值.灰色系统预测主要是基于GM(1,1)模型[18−20].在进行灰色系统建模前需要判断序列是否是光滑序列[18]，数据序列是否满足灰指数规律，然后采用微分拟合法为核心的建模方法.

4.2 涌水量原始数据的预处理

4.2.1 涌水量原始数据的非负序列

设涌水量原始数据的非负序列为

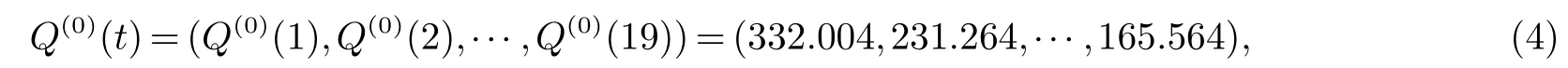
对Q(0)一次累加生成，得序列Q(1)

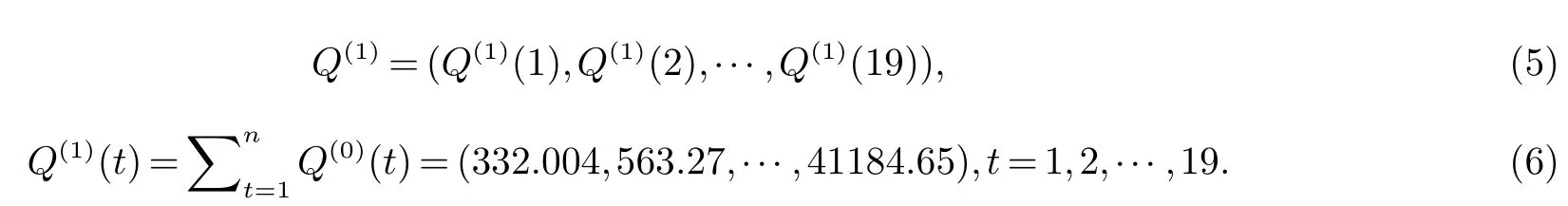
4.2.2 光滑性检验

原始数据序列的光滑程度[17]其光滑性越好，指数规律表现就越明显，预测模型就越精准，同时对于模型的科学性和适用性也就越有利.

检验公式

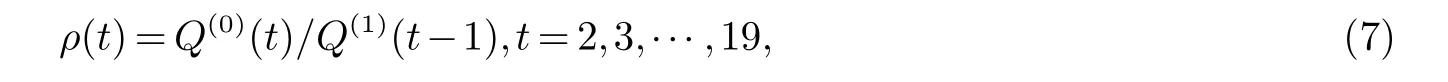
当t>3时，由式（4）计算得到ρ(k)值，见表3，都小于0.5，即δ=0.5，此时数据随机性强，呈近似指数增长规律，故满足建模要求.求级比

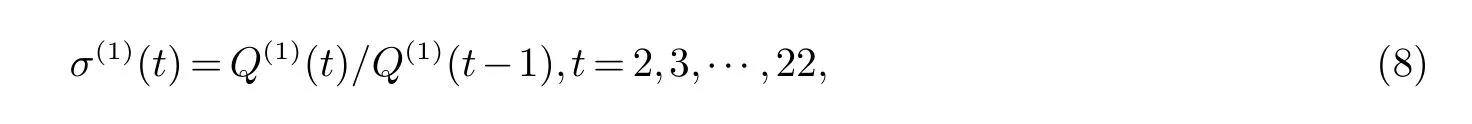
当t>2时，由式（8）计算得到级比值，见表3，在区间[0，0.5]内，级比偏差δ<0.5，可建立Q(1)的预测模型.由于平滑度与级比偏差互为倒数，级比偏差值越小，则平滑度越大，说明光滑性也越好.

4.2.3 紧邻均值生成序列

以一次累加序列Q(1)为基础，构造背景值序列

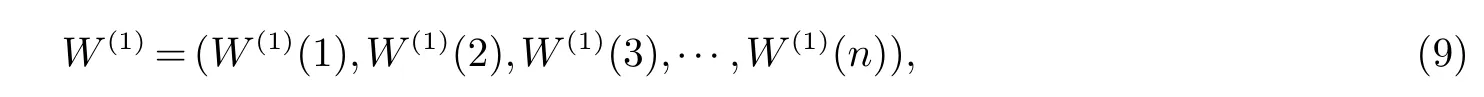
式中，W(1)(t)=u·Q(1)(t)+(1−u)·Q(1)(t−1),t=2,3,···,19.

取u=0.5 时，W(1)(t)为紧邻均值生成序列.

当t=2,3,···,19时，W(1)=(W(1)(2),W(1)(3),···,W(1)(19))=(332.004,231.264,···,165.564).

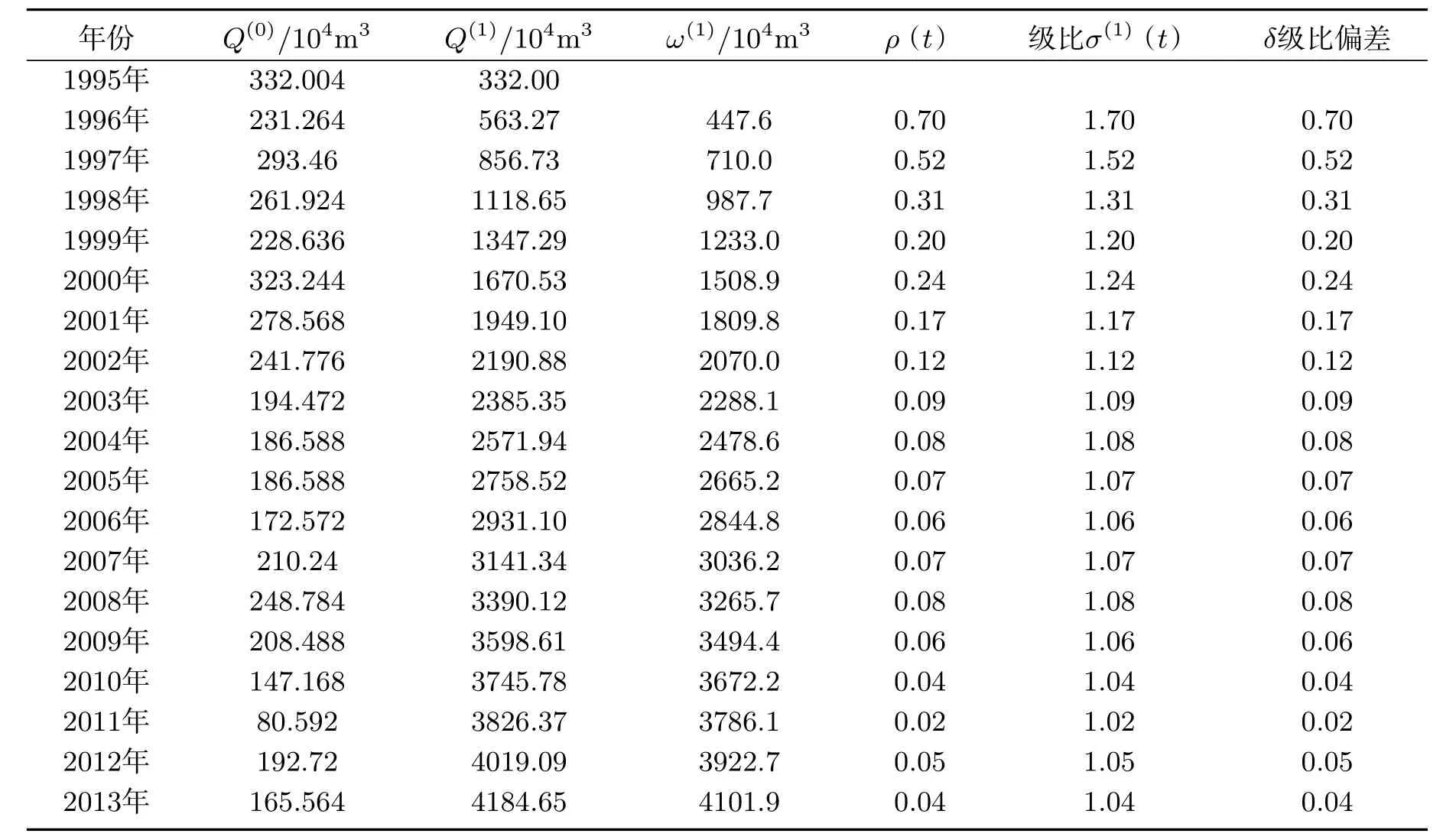
表3 GM（1，1）模型数据分析Tab 3 GM (1,1) Model Data Analysis

4.3 涌水量预测模型的建立及预测

对Q(1)(t),t=1,2,···,22,有微分方程

可得参数：a=0.035，u=299.696.

对（10）式处理，得灰色方程

取Q(1)(0)=Q(0)(1)，得预测公式

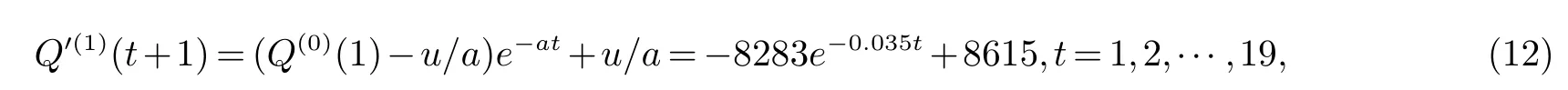
得到序Q(1)的预测序列Q(1)，将Q(1)还原，可以得到序列Q(0)的预测序列

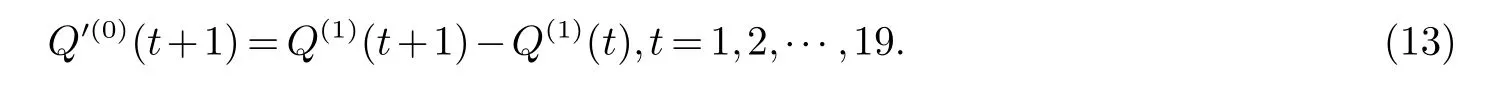
4.4 预测检验

在得到模型参数后，对模型的适用性进行检验，本文采用残差检验，通过各点的相对残差值，可以计算出预测模型的精度值P.

精度等级：一级P≥0.90为优秀；二级是0.80≤P <0.90为良好；三级是0.70< P <0.80为合格；四级是P≤0.70为不合格.若P≥0.8，模型通过残差检验；反之，则必须先修正模型使之满足精度要求，才可进行预测.

该模型平均残差为17.66%，预测精度为82.34%，精度等级为良好.可用于预测老鹰山矿的矿井涌水量.获得相对应的实际涌水量和预测涌水量的动态变化曲线，见图6.2014年至2016年涌水量预测值，见表4.

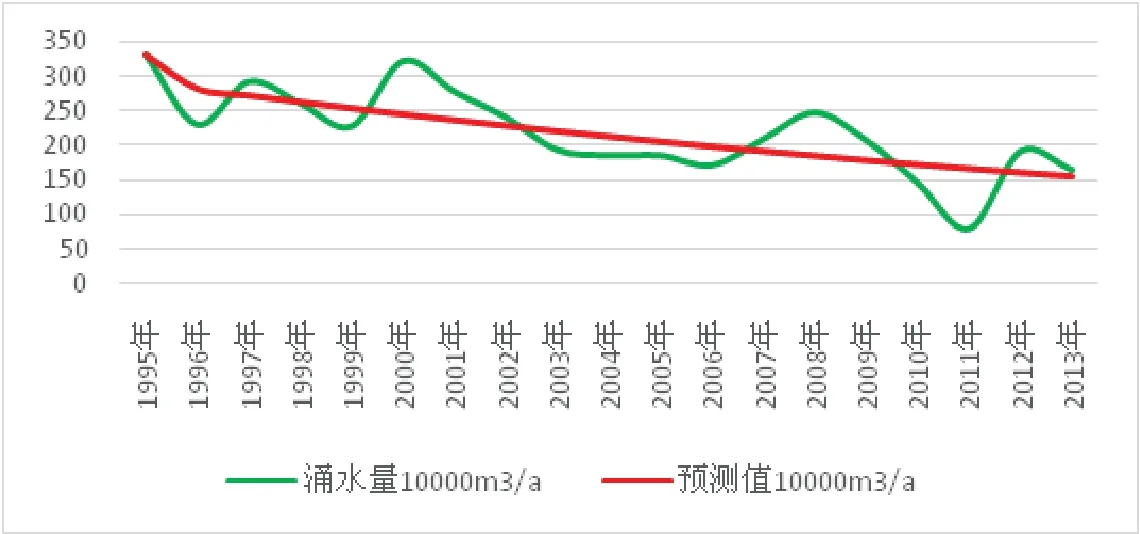
图6 实际涌水量与预测涌水量的动态变化曲线-灰色系统理论Fig 6 Dynamic Curve of Actual Water Inflow and Predicted Water Inflow-Analysis of Grey System Theory

表4 2014年至2016年预测值Tab 4 2014 to 2016 Forecast

5 两种模型结果对比分析

灰色系统理论仅通过观测多年的矿井涌水量来建立模型预测未来几年的矿井涌水量，未考虑其他的影响因素；相关分析法的预测精度要比灰色理论的高，这是由于相关分析法为单变量预测模型，要考虑降雨量的影响.从模型本身我们无法看到影响涌水量的其他因素以及这些因素是如何影响涌水量的变化的.

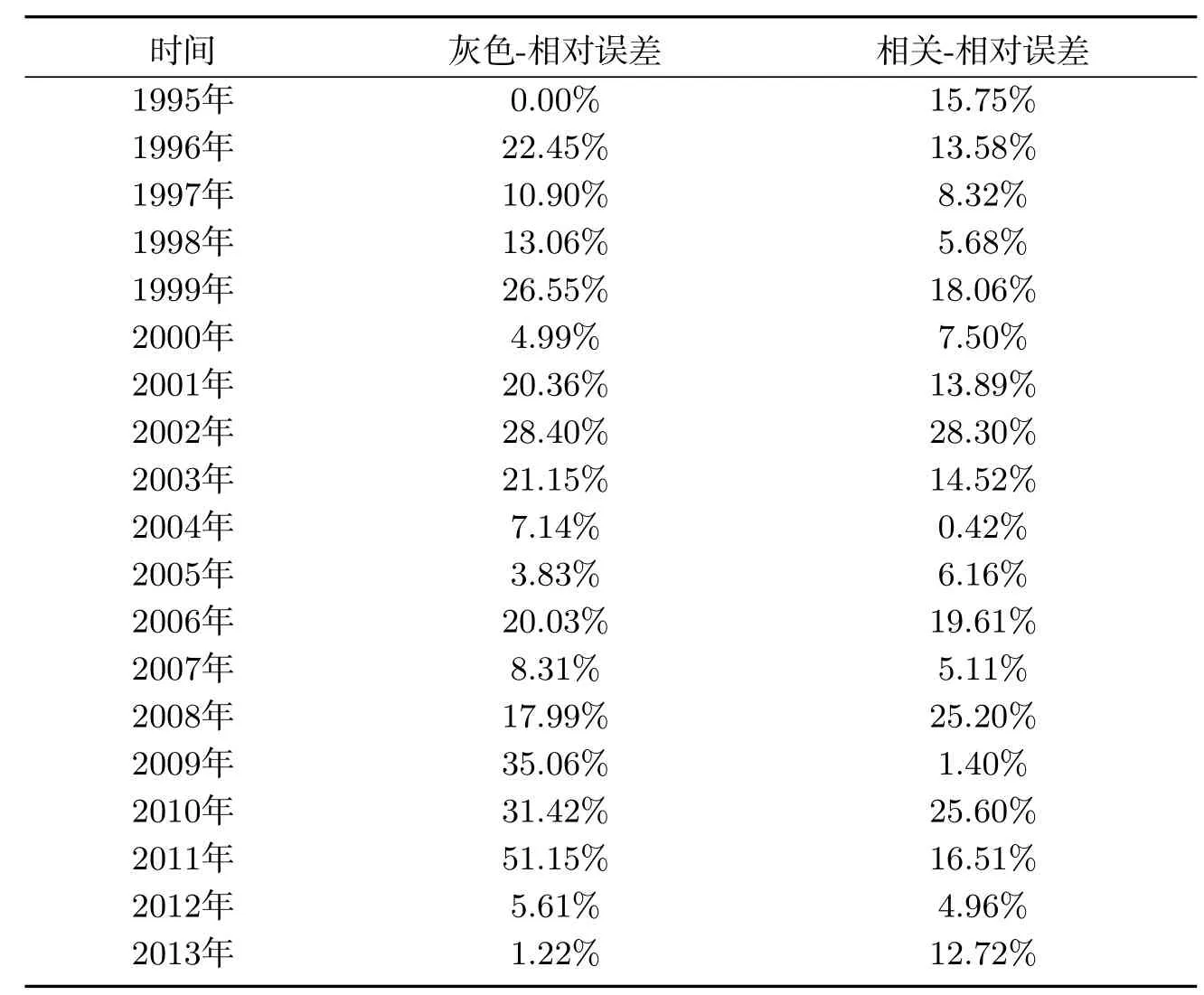
表5 两种方法矿井涌水量实测值的相对误差对比Tab 5 Comparison of Relative Error Between Measured Values of Mine Water Inflow by Two Methods

6 结论

针对老鹰山井田多年的开采，水文地质条件变化巨大、勘查程度不够全面、参数变异系数较大的特点，选用相关分析法和灰色理论预测井田内的矿井涌水量.本文利用SPSS软件对矿区内涌水量与降雨量的相关性建立预测方程及对方程预测精度分析.结果表明：区内涌水量与降雨量密切相关，相关系数为0.835，预测模型的精度达87.19%.灰色系统理论用于解决所获取的资料信息不确定性问题，本文用GM(1,1)模型计算量较小，并用残差检验计算出预测模型的精度值P为82.34%.

相关分析和灰色理论两种方法预测矿井涌水量的结果表明，相关分析的预测结果更为准确.灰色系统理论的GM(1,1)模型是一种单序列的一阶线性动态模型，是变化趋势上预测.相关性分析要考虑降雨量对矿井涌水量的影响，是变化形态上预测.这两种方法对水文地质参数的依赖性少，考虑了涌水量变化的随机性，都适用于长期的预测建模.但是未来对于如何更高效的利用数据结合数值模拟建立更为精准的模型，提高预测精度将会是我们之后的研究方向.