技术进步过程的非线性趋势和异质性特征研究
王必好,张 郁
(山东大学应用经济学博士后流动站,山东 济南 250100)
0 引言
无论是渐进式还是跨越式技术进步,技术创新效率与创造性破坏都在其中产生着差异性作用,体现在效率传导、路径升级、产出增值等方面。渐进式技术进步是由初始阶段n0依次升级到n-1,n,n+1,,技术创新效率向着最优水平接近。而跨越式技术进步不是均匀的,异质性特征明显,受到技术创新效率和创造性破坏强度的双重作用。
与渐进式技术进步相比,跨越式技术进步是确定性技术进步排除技术积累反向作用后的总体变动结果,一次技术进步能够跨越多个阶段,技术积累反而使技术水平向更高阶段升级,其概率为确定性技术进步概率1扣除t时期技术进步由n0阶变动为0阶的技术积累概率P0(t,n0),即1-P0(t,n0),包含着跨越n-1,n,n+1,多个阶段技术进步的可能性,而不是依次渐进实现的[1]。技术跨越间距大且随机波动明显,成果难以充分利用[2]。不同效率技术之间替代的概率是有差异的,技术进步异质性特征明显[3]。技术创新效率引导渐进式技术进步、创造性破坏推动跨越式技术进步,两者具有显著差异,这是此项研究的重点。
本文主要揭示技术创新效率、创造性破坏在渐进式和跨越式技术进步中如何产生差异性作用,技术进步过程是否具有非线性趋势和异质性特征。
1 相关文献综述
国内外文献主要研究技术进步中市场结构、企业规模、企业制度等外生因素。肖文等认为,垄断行业依赖其市场主导地位获得超额利润,没有动力变革新技术[4]。扩大企业规模导致过度官僚控制,阻碍技术创新效率[5]。大企业也可能被锁定在低技术低附加值领域,技术创新效率并不明显[4,6]。而朱有为等认为规模化有利于提升技术创新效率[7]。技术进步的突发点是制度变迁,决定技术进步方向、地点和时机[8]。这些观点以市场竞争、规模选择、制度变化为视角,忽略技术进步与积累的替代关系。可以围绕技术进步过程进行拓展,即新技术替代旧技术,技术积累使技术水平在较低阶段上快速提升。
相关研究剖析创造性破坏、技术创新效率、技术结构等如何引起技术进步内生性变化。技术经济管理水平与技术创新效率是显著正相关,难以显著拉动技术进步[9]。既定技术创新资源多次循环投入使用,提高集约化利用水平[10]。过多追求R&D经费投入规模,而不注重产出投入效率,成果转化效率低[11]。国内战略性新型产业各部门、各阶段中创新与需求存在协同作用[12]。上述内容仅仅反映技术创新效率、创造性破坏与技术进步的局部关系,可以拓展研究其差异化实现路径。
国内外学者探索研究技术创新效率、成果转化、创新收益驱动等内容,研究知识产权形成、信息传递、研发经费投入与创新产出增长之间的关系[13]。技术创新是产出增长的主要驱动力量[14]。提高国有企业自主创新能力,需要建立创新激励机制,促进协同创新[15]。内资、港澳台与外资企业技术创新效率存在差异[16]。但是,这些成果没有研究技术进步中的不确定因素,也没有发现其中非线性趋势和异质性特征,相关研究可以逐步拓展,分析技术创新效率、创造性破坏在不同技术进步方式中作用传导和机制原理等。
本文在前述成果基础上,构建理论分析模型,综合门限自回归 (TAR)和分位数自回归 (QAR)优点,引入康宁等提出的门限分位数自回归 (TQAR)方法[17],研究发现各阶段技术进步是不相关的,概率服从指数分布,具有无后效性,随机特征明显,从而揭示技术创新效率、创造性破坏强度如何形成技术进步非线性趋势和异质性特征。
2 理论模型与分析
2.1 技术创新效率与投入成本函数
技术进步具有内生性特征,在前期积累基础上实现较大突破[18]。技术创新产出函数I是以技术进步阶数n作为自变量,创造性破坏强度μ又是引起n变化的内生因素,均与技术创新效率λ有着技术经济联系:
I=I(λ,n(μ))
(1)
该函数是自变量λ和n递增函数且上凹的。渐进式技术进步中,技术创新效率λ逐渐提升,成果得到充分利用,产出投入比例趋于优化。创造性破坏强度μ通过缩小技术进步阶距,加快旧技术淘汰落后,大幅度拉动技术进步。两者不是独立发挥作用,而是相互关联的,技术进步中不确定性因素增多。以产出投入最优比例为目标,在技术创新投入成本函数c(I,n(μ))基础上构建以下技术创新效率函数:
λ(n(μ))=c(I,n(μ))=n(μ)c(I/n(μ))
(2)
2.2 技术创新效率与创造性破坏强度
技术创新效率引导技术水平从n0阶依次渐进升级到n-1,n,n+1阶。创造性破坏可以跨越多个技术进步阶段,从n0阶直接升级到n+1,n+2,n+3,,间隔距离越大,实现技术跨越的概率越低。假设在n阶技术进步时厂商获得净收益rV(n),构建Bellman方程,反映技术进步净收益构成情况:
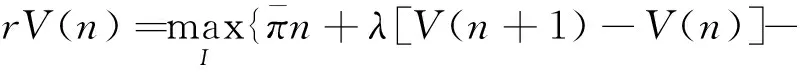
C(I,n)-μn[V(n)-V(n-1)]}
(3)
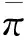
最优技术创新效率的均衡条件是技术进步收益增量等于相应的投入增量。收益增量大于投入增量时,技术创新要素投入量不足,要素配置偏离最优状态,持续投入技术创新要素,将会获得更多收益。收益增量小于投入增量时,产出增量出现递减,技术创新要素投入量过多,创新要素利用效率具有较大提升空间,改善产出投入比例,使既定投入创造更多产出。对Bellman方程求导数,移项后得到最优技术创新效率的实现条件:
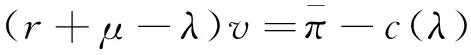
(4)
2.3 渐进式与跨越式技术进步过程
1)μpn+1(t,no)-n(λ+μ)pn(t,no),n≥1
(5)
式 (5)表明,技术创新效率λ引起技术进步由n0阶小幅提升到n-1阶,期望变化率为(n-1)λpn-1(t,n0),立足既定技术创新成果,改善产出投入关系,难以实现大跨度技术进步。创造性破坏强度μ对技术进步促进作用更加明显,推动技术进步由初始水平n0阶跨越升级到n+1阶,技术进步期望变化率为(n+1)μpn+1(t,n0)。然而,创造性破坏强度μ在n0阶向n阶升级时出现阻滞和反转,技术积累效应明显。技术创新效率λ对技术进步拉动作用明显弱于创造性破坏强度μ,两者共同作用对技术进步抵消效应为n(λ+μ)pn(t,n0)。技术积累使原有技术创新成果没有充分利用,被新技术快速替代,浪费技术创新资源。假设技术进步与积累发生在0阶段、1阶段之间,相应的技术进步期望变化率为:
(6)
式 (6)表明,厂商t时期技术积累由n0阶变动到0阶时,技术进步期望变化率等于技术进步变动到1阶时概率与创造性破坏强度μ之积。由此得出假设1:创造性破坏加快技术积累与进步,技术水平在前期积累的基础上快速提升,完成跨越式技术进步,技术创新要素没有得到充分利用,造成一定程度资源浪费。技术创新效率是以渐进方式推动技术进步,难以持续拉动技术水平大幅度显著提升。
(2)跨越式技术进步过程。技术进步由1阶因技术积累回落到0阶,由于创造性破坏带动技术进步向着较高阶段跨越,后阶段技术进步对前阶段没有记忆性,技术进步与积累概率均服从指数分布[3],不是沿着特定的收敛方向持续实现技术进步,其变动过程与结果由式(7)表示。技术创新效率λ、创造性破坏强度μ纳入技术进步过程中,技术积累概率取决于两者比例关系,而且还受到两者变动方向的相互影响。跨越式技术进步过程推导如下:
(7)
P1(t,1)=[1-P0(t,1)][1-r(t)]
(8)
Pn(t,1)=Pn-1(t,1)r(t),n=2,3,
(9)
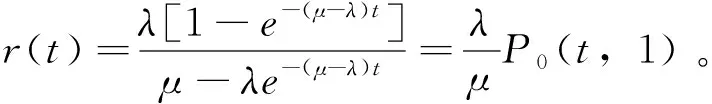
式 (7)表示,厂商t时期技术进步由1阶因为技术积累下降到0阶的概率,取决于技术创新效率λ与创造性破坏强度μ比值以及两者变动方向。当两者保持相同比例变化时,加大创造性破坏强度,促进技术积累与快速升级,而提高技术创新效率,技术进步逐级渐进深化,技术积累渐渐放缓。创造性破坏强度μ加速技术积累,浪费技术创新资源,技术创新效率难以持续提高,但是在较低水平上又实现技术快速进步,技术创新效率λ延缓技术积累速度,平缓技术波动幅度。由式 (7)可知,在两者保持不同比例变化时,当μ>λ,r(t) 只有在技术创新效率和创造性破坏共同作用下,渐进式和跨越式技术进步才能把创新活动引向深入,技术水平持续提高,厂商获得更多创新收益。厂商技术创新收益率受到技术进步不确定性影响,波动起伏较大。厂商在创新收益驱动下,以不同概率实现渐进式和跨越式技术进步,由式(8)(9)推理可得, (10) 式 (10)表明,假设厂商t时期技术进步阶数为n=1,2,,在技术创新收益驱动下,渐进式与跨越式技术进步概率变动关系服从几何分布,具有非线性趋势和异质性特征。厂商在渐进式技术进步中,技术进步由1阶逐渐升级到n阶,技术进步朝着高精尖方向逐渐深化。由此得出假设3:技术创新收益是技术进步的内在动力。渐进式技术进步能够较为准确地定位技术进步方向,优化产出投入比例,达到最优技术创新效率,持续推动技术创新。跨越式技术进步改变技术渐次升级趋势,随机波动特征明显,难以把握其变动方向,技术创新收益没有确定性变化,技术进步呈现非线性趋势和异质性特征。 (11) 模型中,φt-1为t时期之前技术进步全部信息,不同分位点τ把技术进步划分为较低水平、低水平、高水平和较高水平等4个阶段,刻画技术创新效率λ、创造性破坏强度μ对不同类型技术进步的差异化作用。 基本原理是使观察变量估计值向着真实值持续收敛,目标函数预测值无限接近真实值,两者离差逐渐缩小。门限回归系数与门限变量估计值通过优化求解下式获得: (12) 令u=lt-Mlt(τ|φt-1),表示门限分位数回归分析误差,T为样本量,p为滞后期,St(β(τ),η(τ))为目标函数,ρτ(u)为非对称损失函数,且满足以下条件: (13) 非对称损失函数的功能是,寻找最优技术创新效率和创造性破坏强度。技术创新效率降低是因为没有充分利用现有技术创新成果,可以通过提高其利用效率来增加技术进步收益。而创造性破坏由于一次性缩小技术差距而获得创新收益,同时引起现有技术加速折旧,导致技术创新要素过早淘汰,造成闲置浪费。两者引起技术创新收益变动结果不同,应用最小方差原理估计门限值和门限回归系数,其分析过程如下: (14) (15) (16) 数据选取1996—2011年5个高新技术产业,即电气机械及器材业、专用设备制造业、通信设备、计算机及其他电子设备业、仪器仪表及文化办公用机械业、电信和其他信息传输业,作为跨越式技术进步的代表性行业,具有技术更新快、距离较大等特征[9]。而石油和天然气开采业、纺织服装、鞋帽制造业、印刷和记录媒介复制业、化学原料及化学制品业、交通运输设备制造业由于技术替代缓慢,技术进步空间狭窄,以渐次升级方式实现技术进步[20]。研究首先参考各产业技术进步中国家标准拥有情况,细化技术进步分类。跨越式技术进步行业的标准总量达10395件,是渐进式行业的1.42倍,分标准状态看,即将实施类、现行类和废止类分别为301件、6990件和3104件,是渐进式行业的1.67倍、1.50倍和1.24倍。特别是近三年标准数量,跨越式技术进步行业的标准数量为1754件,是渐进式行业的1.70倍。跨越式技术进步行业的技术发明创造和知识更替速度明显高于渐进式技术进步行业。 表1 行业技术进步的国家标准拥有情况分析 注: 资料来源于国家标准化管理委员会官网,数据发布截止时间为2018年6月。 实证分析因变量是当期专利授权量指标,以其滞后一期、滞后二期指标作为自变量,均进行对数化处理,消除可能存在的异方差。数据主要来自中经网、 《中国科技统计年鉴》以及专题研究报告。实证研究使用STATA12.0软件。 门限分位数自回归分析 (TQAR)的门限变量为厂商滞后一期专利授权量指标lt-1。经过门限效应和门限变量个数检验,最优门限数量为3个,将技术进步过程分为较低、低、高、较高4个阶段。渐进式技术进步各阶段分布紧凑,与之对应的门限值相对集中,分别为0.356、0.492和0.677。而跨越式技术进步波动幅度大,创造性破坏作用明显,技术进步两阶段距离较远,门限值分别为0.071、0.418和0.926。技术进步阶段分散,包含着技术创新效率、创造性破坏强度以及随机过程等因素。 (1)分位数自回归 (QAR)和门限自回归 (TAR)分析。QAR分析(见表2)认为,渐进式技术进步在0.10、0.25、0.50、0.75和0.90 5个分位点上滞后一期自回归系数分别为0.294、0.315、0.327、0.545和0.306。波动起伏不大,技术创新效率引导技术进步,路径比较平稳,没有出现发散状态,而是在相对较小的区间内变化。在渐进式技术进步中,滞后二期自回归系数与滞后一期保持基本一致,上下变动相对缓和。 跨越式技术进步在不同分位点上与技术积累交替并存,具有明显的异质性特征,创造性破坏加剧技术进步波动。滞后一期自回归系数由-0.709上升为0.916,然后下降到0.115,再上升为0.694,最后急剧下降为-0.308,总体呈现倒W型变动趋势,技术进步波动较大。滞后二期自回归系数变动幅度较大,变动趋势与滞后一期是相反的,变动趋势是W型的。跨越式技术进步滞后二期自回归系数之间是反方向变动关系,两种变动趋势具有异质性特征。 TAR分析结果表明,渐进式技术进步非线性变化特征并不显著,总体较为收敛(见表3)。特别地,滞后一期自变量作为门限变量,其系数lt-1随着技术进步呈现平稳趋势,从0.537、0.426下降到0.414,最后减少为0.395。滞后二期同样是连续平稳下降的,变动趋势是一维线性的。而跨越式技术进步的3个门限值较为分散(见表4),间隔距离较大。滞后一期自变量作为门限变量,系数先由0.145连续上升0.821、0.947,最后下降到-0.138,在对应3个门限值的区间内变化波动幅度较大,呈现倒V型变动趋势。滞后二期自回归系数随机波动显著,总体出现N型变动趋势。跨越式技术进步在创造性破坏的作用下,非线性特征比较明显,上下波动不规则。但是,门限自回归分析,没有反映技术进步异质性特征,技术变动信息有待于进一步挖掘。 表2 QAR模型的参数估计及检验 注:①***、**、*分别表示1%、5%、10%显著性水平;②括号内数值为稳健标准误差(Robust S.E.);③LR检验假设在有效约束条件下,检验结果表明函数估计值均逐渐接近目标值,模型估计有效;④在跨越式技术进步中,创造性破坏使其实现路径没有遵循分阶段、依次逐步完成的,而是与加速积累同步进行,当技术积累效应明显超过技术进步效应时,相应的截距项和滞后一期、滞后二期自回归系数出现负数,然后在较低起点上快速提升;⑤由上述计量结果可知,Q检验值均小于1%的显著性水平,即滞后两期自变量不存在序列相关;⑥根据AIC检验结果,确定QAR模型滞后阶数为2。 (2)门限分位数自回归分析(TQAR)。相关分析结果见表3。 第一,就异质性特征而言,在wt<0.356、0.356 第二,就非线性趋势而言,四阶段门限自回归与5个分位点的分位数自回归分析构成。在0.10、0.25分位点上,四阶段的自回归系数分别为0.674、0.359、0.641、0.529、0.472、0.392、0.582、0.386,0.593、0.481、0.571、0.408、0.399、0.604、0.368、0.461。而且,随着技术逐渐升级,前阶段技术进步对后阶段变化影响是渐次减弱的。厂商立足于充分利用既定技术创新资源,提高技术创新效率。渐进式技术进步空间持续减少,逐渐转化为一维线性变化趋势。而在0.50、 表3 渐进式技术进步TQAR和TAR模型参数估计及检验 注:①利用网格搜寻法所获得的门限值,可以使残差平方和最小;②LR、Supwald检验,均假设在有效约束条件下。与无约束估计量的似然函数估计值均逐渐接近目标值,模型估计有效;③由上述计量结果可知,各分位点上Q检验值均小于1%显著性水平,即滞后两期自变量不存在序列相关;④根据AIC检验结果,确定TQAR、TAR模型滞后阶数为2。 0.75、0.90的分位点上,自回归系数分别为0.934、0.806、0.882、0.656、0.746、0.524、0.522、0.511,0.452、0.637、0.407、0.596、0.801、0.793、0.714、0.584,0.496、0.509、0.501、0.712、0.528、0.496、0.683、0.597。渐进式技术进步是逐级实现的,具有非线性特征,起伏变化较小,每次技术进步是逐级实现的。技术创新效率发挥着引导性作用,没有创造性破坏等跳跃性、偶然性因素。这个结论验证了假设2是正确的。 跨越式技术进步的门限分位数自回归分析结果见表4。 第一,就异质性特征而言,跨越式技术进步高低变动具有不确定性。门限值0.071、0.418、0.926将技术进步分为4个阶段,在不同阶段波动路径差异较大。对于阶段1,即有wt<0.071,该阶段为较低水平技术进步,所有分位点处自回归系数取值均为正,技术进步在较低水平下没有积累,前期技术进步对当期有正向影响。但是,这种低技术水平下的技术进步具有较大波动性,滞后一期自变量作为门限变量,其系数先由0.114跨越到最高值0.810,然后急剧下降为0.075,再快速提升到0.718,最后降低为0.104,总体呈现倒W型变动趋势,即技术进步在每个分位点上都出现较大波动。相应地,滞后二期自回归系数出现反方向变化,且变化幅度较大,即为正W变动趋势。对于阶段2,为0.071 表4 跨越式技术进步TQAR和TAR模型参数估计及检验 第二,就非线性趋势而言,技术进步方向发生较大拐折,具有显著的不确定性。在0.10、0.75分位点上,滞后一期自回归系数首先由0.114、0.718下降到0.109、-0.209后,持续上升到0.207、0.427,最后上升到0.839、0.724,技术进步路径呈现正V型变化。相应的,滞后二期自回归系数变动有着不同的情况,技术进步非线性特征比较明显,在0.10分位点是由0.984下降为0.753,再上升到0.977,最后下降为0.019,而在0.75分位点上却出现相反的变动趋势,即为正N型变动趋势。在0.25分位点上,滞后一期自回归系数由0.810,快速下降到0.072,又迅速上升到0.519,最后下降为0.216,在3次技术变动中发生两次拐折,技术进步路径是倒N型变化。而滞后二期自回归系数出现相反的变动方向,是正N型变动趋势。在0.50、0.90分位点上,滞后一期自回归系数均由0.075、0.104的较低水平上升到1.524、0.944的较高水平,随后因技术积累快速下降到-0.924、0.116,最后逐步一次变动到0.144、-0.956。而这两个分位点的滞后二期自回归系数均与滞后一期有着较大差异,由0.752、0.964大幅度下降为-0.028、0.012,再上升为0.854、0.994,最后同时快速下降为0.436、0.242。因此,在跨越式技术进步中,滞后一期、滞后二期技术进步成果对现期技术水平产生着不同作用,创造性破坏带来显著的技术积累效应,并在此基础上实现技术水平快速提升,技术进步路径非线性特征明显。假设1、假设3得到论证。 本文重点分析技术创新效率、创造性破坏强度如何引起渐进式和跨越式技术进步,研究技术进步过程中非线性趋势和异质性特征在随机变动、形成机制、作用传导等方面差异,并把门限分位数自回归方法 (TQAR)运用到实证分析中。研究认为,创造性破坏加快技术积累,技术进步在较低水平上得到快速提升。由技术积累引起的技术回落,在创造性破坏作用下不但没有使技术进步停滞不前,而且带来更大幅度跨越。技术创新效率促进研发资源充分利用,引导渐进式技术进步朝着效益目标平稳收敛,非线性趋势和异质性特征不明显。创造性破坏推动技术积累与技术进步交替出现,实现跨越式技术进步,其路径波动变化幅度较大,技术进步具有非线性趋势和异质性特征,为此,提出以下政策建议。 (1)实施信息化带动战略。以信息化加快创新成果扩散应用,提高要素配置精细化水平。坚持数字化、网络化、智能化的方向,引导技术创新要素渗透到实体经济中,积极培育软件定义、数据驱动和智能主导等新模式、新业态。 (2)深化基础研究体制改革。促进新知识、新方法、新原理的源头储备和高效利用,推动跨越式技术进步。积极探索经济合理、技术可行、规模适度的创造性破坏,突破一批关键共性技术。 (3)大力提高技术创新效率。推动创新成果融合到增材制造、工业机器人、集成电路等高新技术领域中,通过知识更新、优化要素配置、提高劳动力素质等途径改善产出投入比例,引导技术创新向内涵延伸。3 实证模型构建和方法
3.1 模型设定
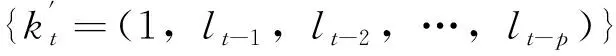
3.2 参数估计
3.3 预测方法


4 实证分析
4.1 数据选取

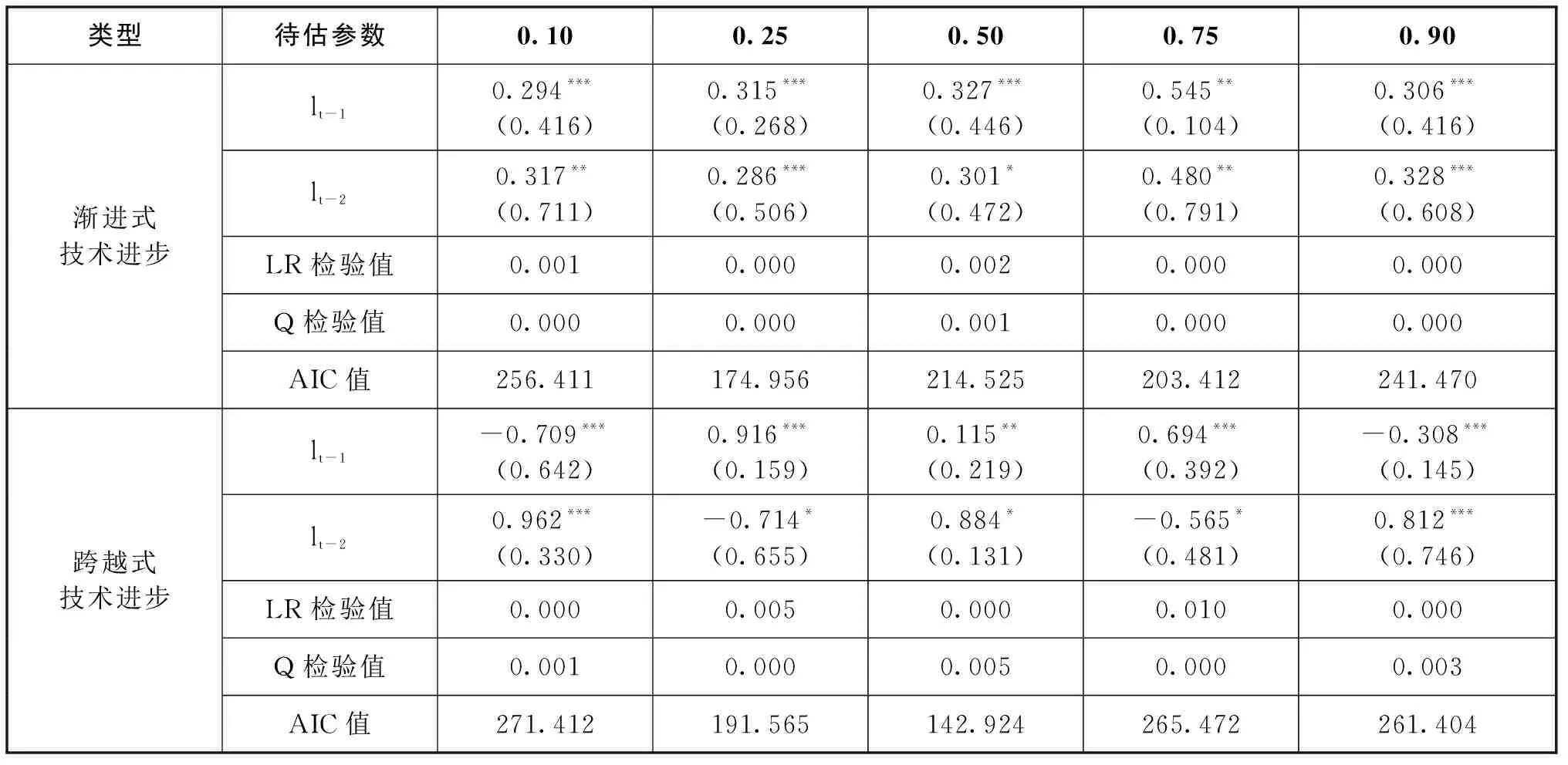
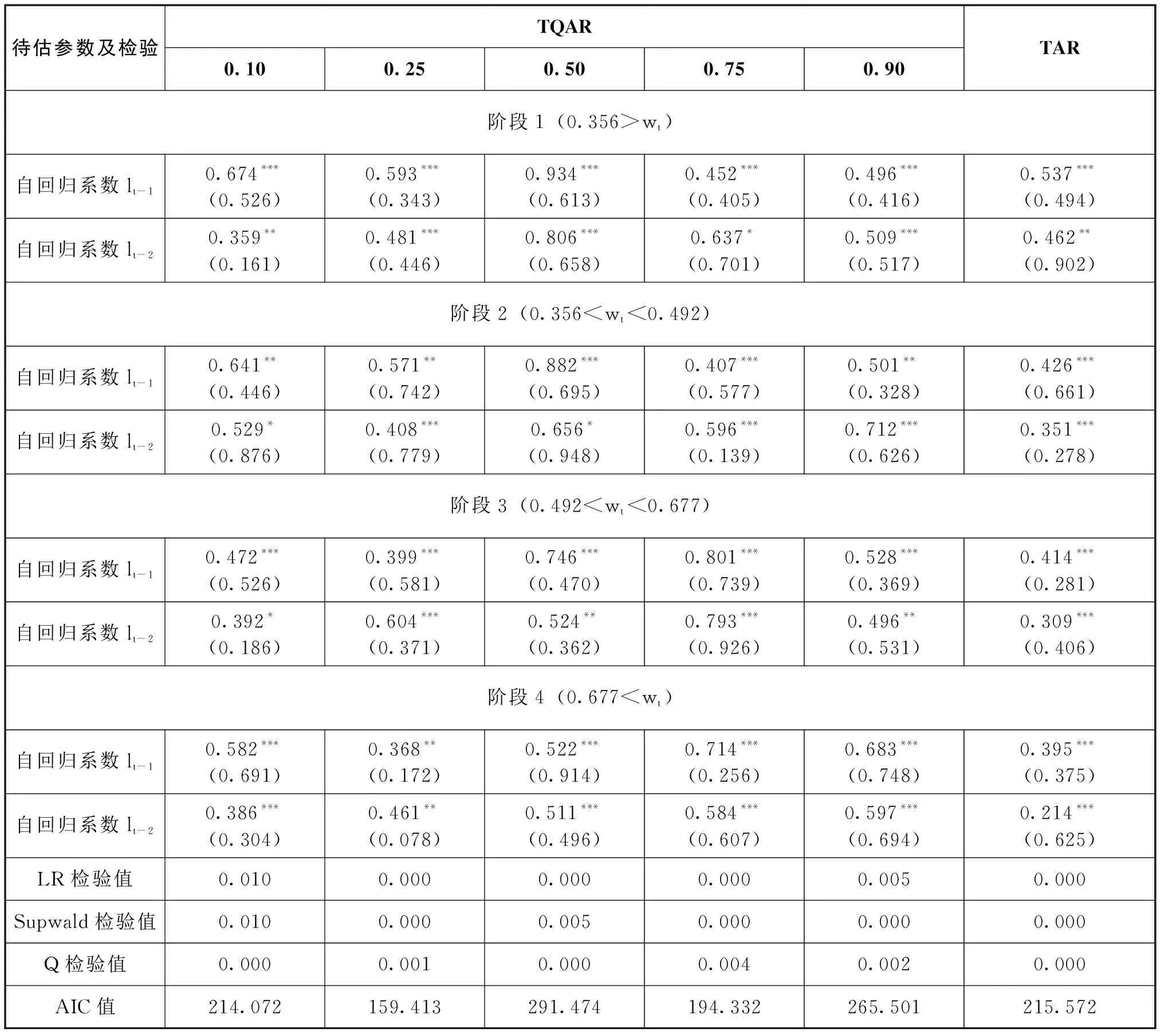
4.2 实证分析

5 研究结论与政策建议

