基于Matlab的水库年径流序列变化周期及趋势性分析
,
(1.华电电力科学研究院有限公司,杭州 310030; 2.中国电建集团华东勘测设计研究院有限公司,杭州 311122)
0 引言
河川径流序列的周期性和趋势性是其演变和波动的重要特征[1],具有多尺度、周期性的特性[2-3],对水利工程的规划、开发、设计和运行具有十分重要的影响[4-5]。尤其是在电力市场改革的推动下,水库调度策略直接影响着发电企业的经济命脉[6],而水库调度策略的制定依赖于水库径流序列的变化周期和趋势。因此,研究水库年径流序列的变化周期和趋势是当下水电企业关心的重要战略问题。
水库年径流时间序列的周期性分析方法有多种,主要有傅里叶分析法、方差分析法、功率谱密度分析法等[7]。鉴于功率谱密度分析法的直观性、唯一性和有效性,本文选择该方法分析水库年径流时间序列的周期性变化。水库年径流时间序列的趋势性分析方法主要有Kendall秩次相关检验法、Spearman秩次相关检验法和线性回归分析法等。线性回归分析法通过线性回归方程的斜率和截距来表现水库年径流与时间的关系,方程的斜率虽然能够表征水库年径流时间序列的平均趋势变化率,却不能判断其趋势性变化是否显著。因此,本文的水库年径流序列的趋势性变化分析选择Kendall秩次相关检验法和Spearman秩次相关检验法,并通过线性回归分析法进行分析校对。
本文以某流域龙头水库62个水文年(1952—2013年)的年径流序列为研究对象,基于大型数学软件Matlab,采用功率谱密度分析法进行龙头水库年径流序列的周期分析,采用Kendall秩次相关检验法和Spearman秩次相关检验进行龙头水库年径流序列的长期变化趋势分析,以期得到该流域长期的水文序列变化规律。
1 工程概况
某流域全长100余km,多年平均降雨量1 670 mm。该流域龙头水库正常水位为330.0 m,设计洪水位为338.0 m,为不完全多年调节性水库。根据水量平衡原理和电网水库历年逐月入库流量统计表,可以得到龙头水库坝址逐月平均流量资料。龙头水库坝址多年平均流量85.32 m3/s,年平均径流量为26.91×108m3,坝址处各水文年年径流见表1。

表1 龙头水库1952—2013年水文年年径流序列Tab.1 Leading reservoir annual hydrologic runoff series from 1952 to 2013 m3/s
2 计算分析
2.1 周期分析
2.1.1 功率谱分析模型建立
龙头水库年径流时间序列Qt(t=1,2,…,n)的功率谱分析的步骤如下。
样本落后自相关系数
(1)

平滑功率谱
(2)
(3)
式中:Bl为平滑窗参数;P为径流序列中所有对偶值,即最大落后步长;l为波数(l=0,1,2,…,P);m为计算波数最大值;r为自相关系数。
根据式(1)~(3)的运算结果制作功率谱图。最后对功率谱估计值的显著性进行检验。
取最大落后步长P=30,计算结果如图1所示,龙头水库的功率谱估计值曲线的峰值点对应的周期分别为3年、10年和24年。
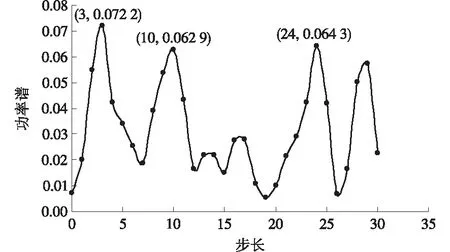
图1 连续功率谱Fig.1 Continuous power spectrum
2.1.2 谱估计的显著性检验
依据连续功率谱显著性检验原理,龙头水库序列落后1个时刻的自相关系数r1小于信度α=0.05,采用白噪声谱进行谱估计的显著性检验。计算结果表明,对应白噪声谱95%的否定域的上限值为0.077 0,而龙头水库的功率谱曲线的峰值点值为0.072 2,小于否定域上限值,因此认为龙头水库坝址实测年径流量序列无显著性周期存在。
2.1.3 与运行资料的分析对比
根据电网公布的该电站1982—2013年的上网电量,可以得到龙头水电站该期间逐月平均流量资料和水文年资料。如图2所示,龙头水电站多年平均发电量6.08 亿kW·h,32个水文年的发电高峰和低谷具有1个3年的小周期循环, 1995年之前的发电周期显著,但近年来的发电周期不显著。

表2 Spearman秩次相关检验法秩次序号Tab.2 Rank number of Spearman rank correlation test

图2 龙头水库各年发电量序列Fig.2 Annual power generation series of the leading reservoir
2.2 趋势性分析
2.2.1 Kendall秩次相关检验法
根据Kendall秩次相关检验法计算相关性
(4)

将表1的年径流序列值代入式(4)进行统计计算,N=62,P=843,τ=- 0.108,Var(τ)=0.007 6,最终可得U=-1.25<0,说明年径流序列呈下降趋势;|U|小于α=0.05下的检验值1.96,说明在显著性水平α=0.05下龙头水库年径流序列呈下降趋势且趋势不显著。
2.2.2 Spearman秩次相关检验法
Spearman秩次相关检验法的显著性
(5)
(6)
式中:γs为龙头水库年径流序列的相关系数;t为水库年径流时间序列的顺序号,dt=Rt-t,Rt为水库年径流时间序列的正序(从大到小)序号。由于T服从于(N-2)的t分布,因此需要分析其在显著性水平α下,即|T|>tα/2是否成立,如果成立,则说明龙头水库年径流时间序列的变化趋势显著,反之不显著。
将表(1)的年径流序列值代入式(5)进行统计计算,计算结果见表2,最终得γs=0.168,T=1.31。由于T小于α=0.05下的检验值2.01,该水库年径流时间序列下降趋势不够显著。
2.2.3 与线性回归分析对比

续表
线性回归法通过建立水文序列Q(t)与其时序t之间的回归方程,该方法可以给出时间序列是否具有递增或递减的趋势。回归方程为
Q(t)=kt+c,
(6)
式中:Q(t)为径流序列;k为直线的斜率;c为截距。
为了验证上述两种趋势性检验的准确性,用线性回归法分析龙头水库坝址1952—2013年(水文年)实测年径流序列的变化趋势,结果如图3所示。

图3 龙头水库年径流序列线性回归法分析趋势示意Fig.3 Trend of annual runoff series of the leading reservoir analyzed by linear regression method
该线性回归方程为y=-0.0634x+152.63(R2=0.021 7)。由k<0可知,该龙头水库坝址处的年径流序列有着缓慢下降的趋势。
3 结论
本文基于Matlab软件,采用功率谱分析法对某流域龙头水库坝址年径流序列资料进行分析,并与实际运行资料进行对比,得到该水库坝址年径流序列无显著周期存在,但存在3年、10年和24年的微弱振荡周期。利用Kendall和Spearman秩次检验法分析得到该水库坝址年径流序列的变化趋势,并与线性回归分析法相校对,均得到龙头水库年径流时间序列呈缓慢减少趋势,但趋势性不够显著的结论。

