不同湍流模型在三维后台阶数值模拟中的对比

王宇航，赵劲彪，辛 亮

(1.中国航空研究院，北京 100012； 2.北京航天发射技术研究所，北京 100076； 3.重庆交通大学 交通运输学院，重庆 400074)

0 引言

随着近几十年来计算机技术的不断发展，计算流体力学(Computational Fluid Dynamics，CFD)技术迅速发展，被广泛应用于航空、航天、船舶、汽车、建筑、环境和化工等多个领域，取得了很大的成就[1]。湍流模型是CFD领域最重要的成果，是制约CFD精确计算的关键之一，是计算流体工程师们最关注的话题[1]。其中，基于Boussinesq涡黏性假设的一方程Spalart-Allmaras(简称SA)湍流模型[2]和两方程k-Omega SST(简称SST)湍流模型[3]由于良好的鲁棒性和对逆压梯度和小尺度分离的良好预测[1]，成为了工程应用的主流方法。然而，由于Boussinesq涡黏性假设基于各向同性假设，所以难以反映湍流各向异性的特点，对大分离流动等各向异性较强的复杂流动模拟效果并不太好。

雷诺应力模型(RSM)通过直接求解以雷诺应力为变量的输运方程，能更好地反映湍流的各向异性特征，较适用于强分离流动[4]。但是，在求解三维问题时，需要额外求解6个雷诺应力方程，计算工作量巨大[5]。为了克服雷诺应力模型计算量大的缺点，研究者们发展了适用于三维湍流计算的显式代数雷诺应力模型(EARSM)，并开展了许多研究工作[6-9]。

后台阶流动是典型的大分离流动，学术界围绕后台阶流动开展了大量的实验工作[10]，是检验湍流模型优劣的理想力学模型之一。

因此，本文将对EARSM进行详细地阐述，并结合三维后台阶实验模型加以验证，与经典的湍流模型(SA和SST)进行比较，表明三种湍流模型的优劣。

1 计算方法

本文采用RANS方程进行模拟，在计算空间生成多块结构网格，采用有限体积法进行求解，空间离散格式为二阶迎风格式，时间推进格式为四阶Runge-Kutta方法，采用多核并行计算并引入多重网格加速技术，以提高计算效率。

1.1 控制方程

在直角坐标系下，三维非定常可压缩雷诺平均Navier-Stocks方程(RANS)可表达成如下形式：

其中，F1和FV分别代表无粘和有粘通量矩阵，Q代表源项向量。为了封闭RANS方程，采用SA、SST和EARSM分别封闭湍流模型，SA和SST较为常见，推导过程见文献[10]。EARSM推导过程如下一小节所示。

1.2 显式代数应力模型[3](EARSM)

雷诺应力模型(RSM)是指直接对N-S方程进行雷诺平均所得到的方程，由于存在很多无法直接进行数值模拟的项目，所以需要对这些分量项进行模化。而在弱平衡限制条件下，EARSM方法就是近似的雷诺应力模型。由于添加了各项异性张量aij，因此在非平衡流中表现很好。

EARSM可以通过基于Mentera的两方程模型进行模化：

式中，湍流黏性系数定义为

雷诺应力的定义为

模型采用的参数为

β*=0.09，γ=0.55317F1+0.4403547(1-F1)，β=0.0750F1+0.0828(1-F1)，σk=0.5F1+1.0(1-F1)，σw=0.5F1+0.856(1-F1)，σω2=0.856

其中，y是网格点到壁面的距离，CDkω是ω输运方程中的交叉项。

和原有的两方程模型所不同的是，在雷诺应力项的定义中，多了一项额外的各向异性应力分量，从而体现了流体的各项异性特性，各向异性分量表述如下：

2 计算模型及结果分析

2.1 后台阶实验模型

后台阶实验算例很多，但是以Driver和Seegmiller的后台阶实验计算数据最为完整详细，Driver后台阶实验由NASA与斯坦福大学湍流研究中心共同完成，实验获取数据为台阶下游的空间速度型和雷诺应力特征[10]。空间速度型特征和雷诺应力特性采用激光多普勒测速仪(LDV)进行测量。本文采用的也是这个算例进行后台阶模型的校核验证，实验装置如图1所示。

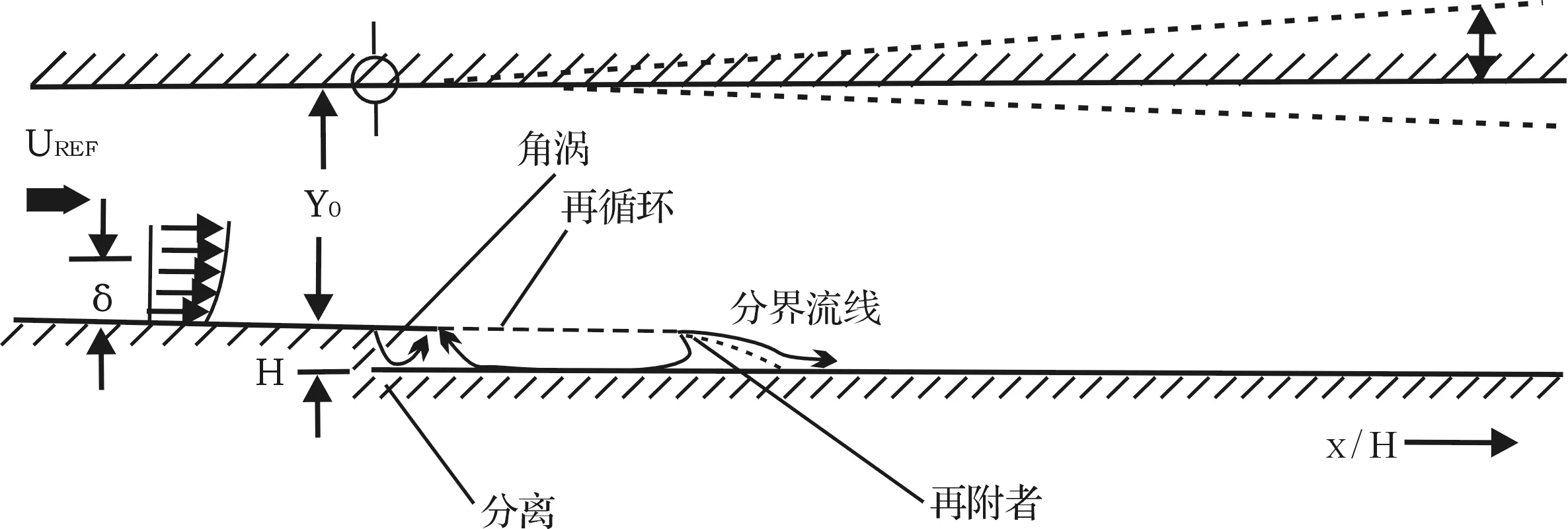
图1 后台阶风洞模型(H=12.7mm，Y0=8H)

2.2 后台阶三维模型数值模拟

为进行数值模拟，需要对风洞物理模型进行几何简化。简化后的风洞主要参数：实验段入口到台阶距离800mm，台阶到实验段出口的距离1000mm，可以保证流动充分发展。实验段高度100mm。实验段湍流度小于1.0%。实验装置后台阶高度H=12.7mm。

图2三维整体网格

为了对各种湍流模型进行计算结果对比，分析各种湍流模式对于计算分离流动的优劣，数值模拟采用三维结构网格。三维模型的优点在于最大程度的模拟实验状态，因而可以计算出流动的三维效应，对数值模拟结果更精确一些。三维模型网格点数目为315441，数值模拟来流速度44.2m/s。整体网格如图2所示。

对于三维模型，取展向中心截面处的流场数据作为三维数值模拟结果。各站位位置及对应物理区域如图3所示(H,2H,4H,8H)。计算结果与风洞实验结果速度型对比如图4所示。

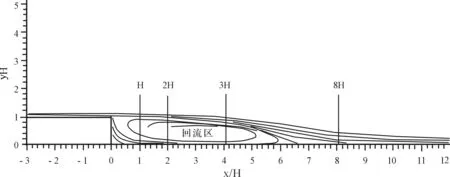
图3 站位位置示意图

图 4 各站位计算结果对比

从图4可以看出，在1H处，SA模型对于回流区模拟结果较差，SST与EARSM模型在回流区和剪切层模拟都比较好。在2H处，SA同样表现了其对于回流区模拟的不足，在这个区域EARSM比SST模拟结果要好一些，但是在剪切层，SA数值模拟的结果要优于其他两种湍流模型。在4H处，在回流区域，SST与EARSM模型模拟结果都与实验数据接近，而SA模拟结果偏小。在8H处，当流动已经流过后台阶分离涡时，三种模型模拟结果都符合了实验流动发展的趋势，在剪切层SA的模拟结果要稍微好一点。综合来说，EARSM模型对于回流区分离涡的模拟较好，在剪切层位置其模拟结果也和实验较为接近，能较好地反映后台阶的分离流动。

3 结语

针对分离流动中典型的后台阶流动，采用SA、SST和EARSM进行了数值模拟，并与实验结果进行了对比，得到了以下结论：

(1)EARSM对于后台阶分离涡回流区的模拟结果最好，要优于SA与SST湍流模型，SA模型对于剪切层模拟稍好一点。

(2)EARSM模型对于后台阶回流区分离涡的模拟较好，在剪切层位置其模拟结果也和实验较为接近，能较好地反映后台阶的分离流动。