基于BP神经网络的棉花颜色级预测

李 帅 单国华 贾丽霞 钟 民 刘 瑞

(1.新疆大学，新疆乌鲁木齐，830046;2.新疆维吾尔自治区纤维检验局，新疆乌鲁木齐，830026)

棉花颜色级检验体系是通过大容量棉花纤维测试仪(HVI)来进行棉花反射率Rd和黄度值+b的测定，并依据颜色分级图定出棉花颜色级。颜色级检验体系有利于我国棉花在棉花质量检验指标体系以及检验方法上与国际通行做法全面接轨，更加有利于中国棉花产业健康发展[1-2]。然而，HVI测定棉花的颜色级必须在严格的条件下进行，不能实现棉花颜色级的实时检测[3]。

测色配色仪在纺织相关企业使用广泛，设备价格相对便宜、操作简单、使用方便，且不需要专业的测试条件，主要用于纺织品的白度、黄度以及染色织物颜色的测试等[4]。该仪器测得的棉纤维色度参数明度值L*，即试样颜色的明亮程度；L*值越大表示试样颜色越亮，越小表示颜色越暗。棉纤维色度参数黄度值b*，反映的是黄色和蓝色之间的色度，负值表示试样颜色偏蓝，正值表示试样颜色偏黄。这与HVI测得的反射率Rd、黄度值+b的物理意义是一致的。在此基础上，国内陆永良等人以及国外Devron等人采用线性回归的方法证明了测色配色仪参数L*、b*与HVI测定棉花的Rd、+b之间线性相关，但对于棉花颜色级与测色配色仪测定的色度参数之间关系的研究较少[5-6]。经过前期的研究，发现颜色级和色度参数间是非线性相关的关系，而BP神经网络算法是应用较多的一种前馈式学习算法与反向传播算法的神经网络，它可以充分逼近任意复杂的非线性关系。本文研究了基于BP神经网络构建棉花颜色级与棉纤维色度参数L*、b*之间的关系，为实现棉花颜色级快速、及时、便捷的检测提供基础[7-8]。

1 试验部分

1.1 试样规格

棉花试样总共280份，每份250 g，所有试样均为市场流通的新产棉花。

1.2 测试方法

1.2.1 颜色级测试

根据GB/T 20392—2006《HVI棉纤维物理性能试验方法》，采用乌斯特HVI 1000型大容量棉花纤维测试仪确定棉花颜色等级。

1.2.2 色度参数测试

根据GB/T 17644—2008《纺织纤维白度色度试验方法》，采用Hunter Lab UltraScan PRO型测色仪测试色度参数。从每份棉花试样中随机抽取5个小样(小样规格为600 mg/个)，每个小样正反面各测试一次，得到10组数据，经算术平均后得到该份棉花试样的色度参数L*、b*值。

1.3 BP神经网络模型建立

1.3.1 BP神经网络数据选择

280份棉花试样共采得颜色等级11个。对每个颜色等级随机抽取5份，共计55份。从这55份试样中随机抽取10份作为测试组F0进行本次试验研究，剩余的45份作为BP神经网络的训练组[9]。

1.3.2 BP神经网络数据前处理

为了减弱主控因素L*、b*不同量纲的数据对网络模型训练与预测的影响，在BP神经网络训练前，应对两个主控因素归一化处理[10]。采用premnmx函数将输入变量L*、b*归一化到[-1，1]之间，具体的调用格式为：

[p1,minP,maxP,t1,minT,maxT]=premnmx(P,T)

输出变量反归一化函数为postmnmx，具体调用格式为：

A=postmnmx(B,minT,maxT)

式中，P为输入变量矩阵，minP、maxP分别为输入变量最小值和最大值，T为输出变量矩阵，minT、maxT分别为输出变量最小值和最大值，B为归一化预测值矩阵，A为预测值矩阵。

1.3.3 BP神经网络模型结构设计

输入输出神经元个数选择：选择棉纤维色度参数L*、b*作为输入变量，棉花颜色级作为输出变量[11]。设置BP神经网络输入层的神经元个数为2，输出层的神经元个数为1。

隐层层数选择：BP神经网络是在输入层与输出层之间增加一个或几个隐含层，隐含层层数越多，精度越高，网络结构越复杂，训练时间越长。综合考虑后，本文隐含层选用1层[12]。

隐层神经元个数选择：由公式(1)确定[13]。

(1)

式中,N为隐层神经元个数，n为输入神经元个数，m为输出神经元个数，a为1～10之间的常数。为了提高预测精度，建立的BP神经网络拓扑结构为2-N-1，经计算得，N的取值范围为3～12，通过网络模拟训练，根据相关系数和训练误差最小值确定N值。

1.3.4 BP神经网络的实现过程

采用MATLAB软件编程来实现BP神经网络的建立。采用三层网络，隐含层传递函数为tansig，输出层传递函数为purelin，网络训练函数为traingdx。编程代码主要部分如下：

[p1,minP,maxP,t1,minT,maxT]=premnmx(P,T)；%输入输出变量归一化

net=newff(minmax(p1),[N,1],{'tansig','purelin'},'traingdx')；%建立BP神经网络

[net,tr]=train(net,p1,t1)；%进行网络训练

A=premnmx(O)；%测试变量归一化

B=sim(net,A)；%仿真

C=postmnmx(B,minT,maxT)；%反归一化

1.4 BP神经网络方法的稳定性分析

从剩余的225组棉花试样中随机选取3组作为测试组，分别记为F1、F2和F3，每组10个棉花等级进行预测，对预测结果进行分析，评估BP神经网络预测棉花颜色级的稳定性。

2 结果与讨论

2.1 BP神经网络模型隐层神经元个数的确定

以2个棉纤维色度参数L*、b*作为输入变量，以棉花颜色级作为输出变量，隐含层神经元个数为3～12，使用45个训练样本数据进行模型训练后，得到这10个棉花颜色级预测模型，其训练误差和相关系数见图1。

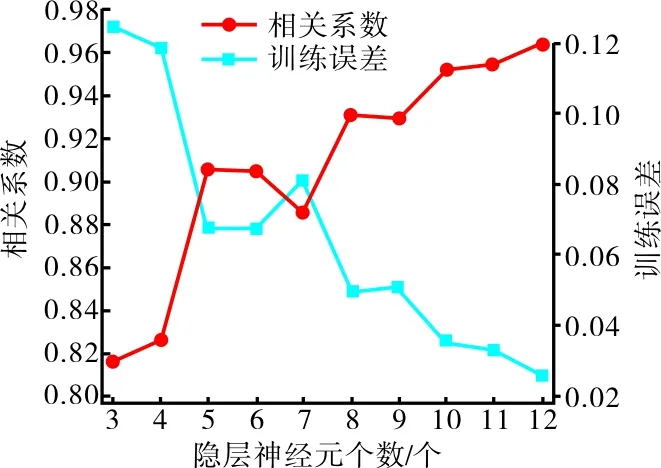
图1 不同隐层神经元个数的相关系数和训练误差图

由图1可以看出，当隐层神经元个数从3个增加到12个时，相关系数整体呈上升趋势，训练误差整体呈下降趋势。隐层神经元个数为12个时，相关系数达到极大值0.965，训练误差降低到最小值0.026。因此，确定BP神经网路的拓扑结构为2-12-1。

2.2 BP神经网络模型训练样本回归直线

采用MATLAB软件编程，对45个训练数据进行学习，得到BP神经网络模型训练样本回归直线见图2。

图2 BP神经网络模型训练样本回归直线

网络目标X与网络输出Y的相关系数R=0.968 39，回归直线方程为Y=0.93X-0.009 2。从图2中可以看出，经过该BP神经网络模型训练学习，棉纤维色度参数L*、b*与颜色级具有很强的相关性，说明该BP神经网络模型可用于棉花颜色级预测。

2.3 BP神经网络预测值和实测值结果与分析

将根据1.3.1抽取的10组测试数据分别进行测试试验和BP神经网络预测，得到了BP神经网络预测值分别为11.57、12.51、12.89、24.50、22.91、23.52、32.10、30.62、33.70、41.45；相应的试验实测值为11、12、13、22、23、24、31、32、33、41。对预测值和实测值数据进行回归分析，得到回归直线方程为Y=0.992 4X+0.566 7，见图3。

图3 BP神经网络预测值与实测值线性回归直线

实测值X与预测值Y最大相对误差为11.36%，最小相对误差为0.4%。由图3可知，棉花试样颜色级的实测值X与BP神经网络预测值Y回归直线中可以看出两组数据间拟合优度为99%。说明以棉纤维色度参数L*、b*为主控因素所建立的BP神经网络模型，经过对数据的训练和学习，可以对棉花颜色级进行预测，预测值与实测值基本吻合。

2.4 BP神经网络模型的稳定性分析

随机选取,3组数据F1、F2、F3，经BP神经网络模型预测后，对实测值与BP神经网络预测值进行分析，结果见表1。

表1不同测试组的稳定性测试结果

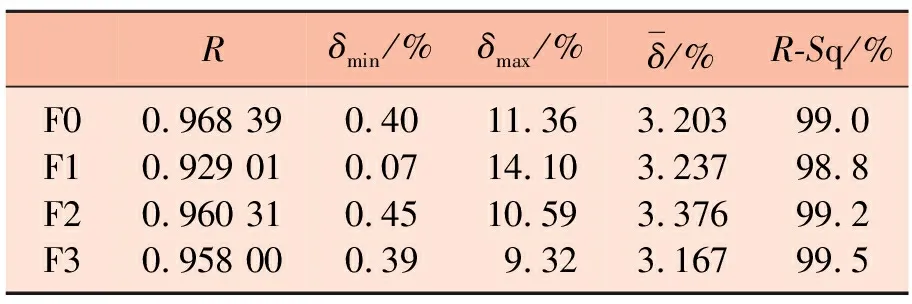
Rδmin/%δmax/%δ/%R-Sq/%F0F1F2F30.968 390.929 010.960 310.958 000.400.070.450.3911.3614.1010.599.323.2033.2373.3763.16799.098.899.299.5

从表1中可以看出最小相对误差和最大相对误差均在F1组，F2、F3这两组中的数据与F0组较为接近。总体来说，F1、F2、F3这3组数据中相关系数、平均相对误差和拟合优度的值均与F0组相差较小，因此该方法具有一定的稳定性。

3 结论

为了实现棉花颜色级的方便快捷检验，通过BP神经网络对棉花色度参数与棉花颜色级之间的关系进行了研究，主要得到以下结论。

(1)采用色度参数L*、b*作为输入变量，棉花颜色级作为输出变量，采用三层网络，BP神经网路的拓扑结构为2-12-1，经过对采集数据进行训练建立了BP神经网络模型。

(2)通过对BP神经网络预测值与实测值数据进行对比分析，实测值与预测值最大相对误差为11.36%，最小相对误差为0.4%，预测值和实测值的数据间具有很强的相关性，说明所建立的BP神经网络模型具有较好预测效果。

(3)F1、F2、F3这3组数据中相关系数、相对平均误差和拟合优度的值均与F0相差较小，建立的BP神经网络模型的稳定性较好。