刷式-迷宫密封泄漏流动和转子动力特性数值研究

张元桥,李志刚,李军,晏鑫

(西安交通大学叶轮机械研究所,710049,西安)

刷式密封的泄漏量仅为传统迷宫密封的10%～20%,柔性的刷丝束对于转子的偏心运行具有极强的适应性,因此刷式密封在航空发动机、燃气轮机和蒸汽轮机中得到广泛应用[1]。刷式密封由于运行过程中刷丝束的磨损严重,降低了封严性能,目前发展的刷式-迷宫密封比传统迷宫密封具有更优异和相比于典型刷式密封具有更持久的封严性能[2]。

科研人员采用实验测量和数值模拟的方法研究了刷式密封泄漏流动机理。Schur等实验研究了传统焊接型刷式密封和箍制刷式密封的刷丝束内部压力分布[3]。Li等采用多孔介质模型研究了迷宫刷封的泄漏流动特性,分析了转速、压比和刷丝束与转子间隙对泄漏流动特性的影响规律[4]。Dogu等采用数值方法详细总结了刷式密封结构参数和运行工况对密封泄漏流动特性的影响[5]。

刷式和迷宫密封会产生流体激振力,影响转子系统的稳定性。Conner等实验研究了4级刷式密封的转子动力特性,实验结果表明,4级刷式密封的转子动力特性系数随实验参数变化较小,且转子动力特性优于八腔室的迷宫密封[6]。Laos等实验研究了刷式-袋型阻尼密封的转子动力特性,实验结果表明,在袋型阻尼密封出口处增加刷式密封,其阻尼系数是原始袋型阻尼密封的2～3倍[7]。Pugachev等发现增设刷式密封能够改善迷宫密封的转子动力特性[8]。Gaszner等实验和数值研究了刷式-迷宫密封泄漏流动和转子动力特性,并利用简单力学模型估计了刷丝接触产生的机械刚度[9]。Yuan等采用三维模型数值计算了刷式密封围栏高度、刷丝束厚度、刷丝束与转子间隙等几何参数对刷式密封转子动力特性的影响规律[10]。陈尧兴等研究了基于涡动模型的迷宫密封转子动力特性系数数值预测模型和影响因素[11-12]。

目前,刷式-迷宫密封的转子动力特性数值预测数学模型尚不完善。本文采用基于涡动转子法的计算流体动力学方法,并利用非线性Darcian多孔介质模型模拟刷丝束内部的流动,建立了刷式-迷宫密封泄漏流动和转子动力特性系数数值预测模型,研究了压比、进口预旋、转子自旋速度对刷式-迷宫密封泄漏流动和转子动力特性系数的影响,并与迷宫密封进行了比较,以期为刷式密封的设计和转子动力特性系数预测提供参考。

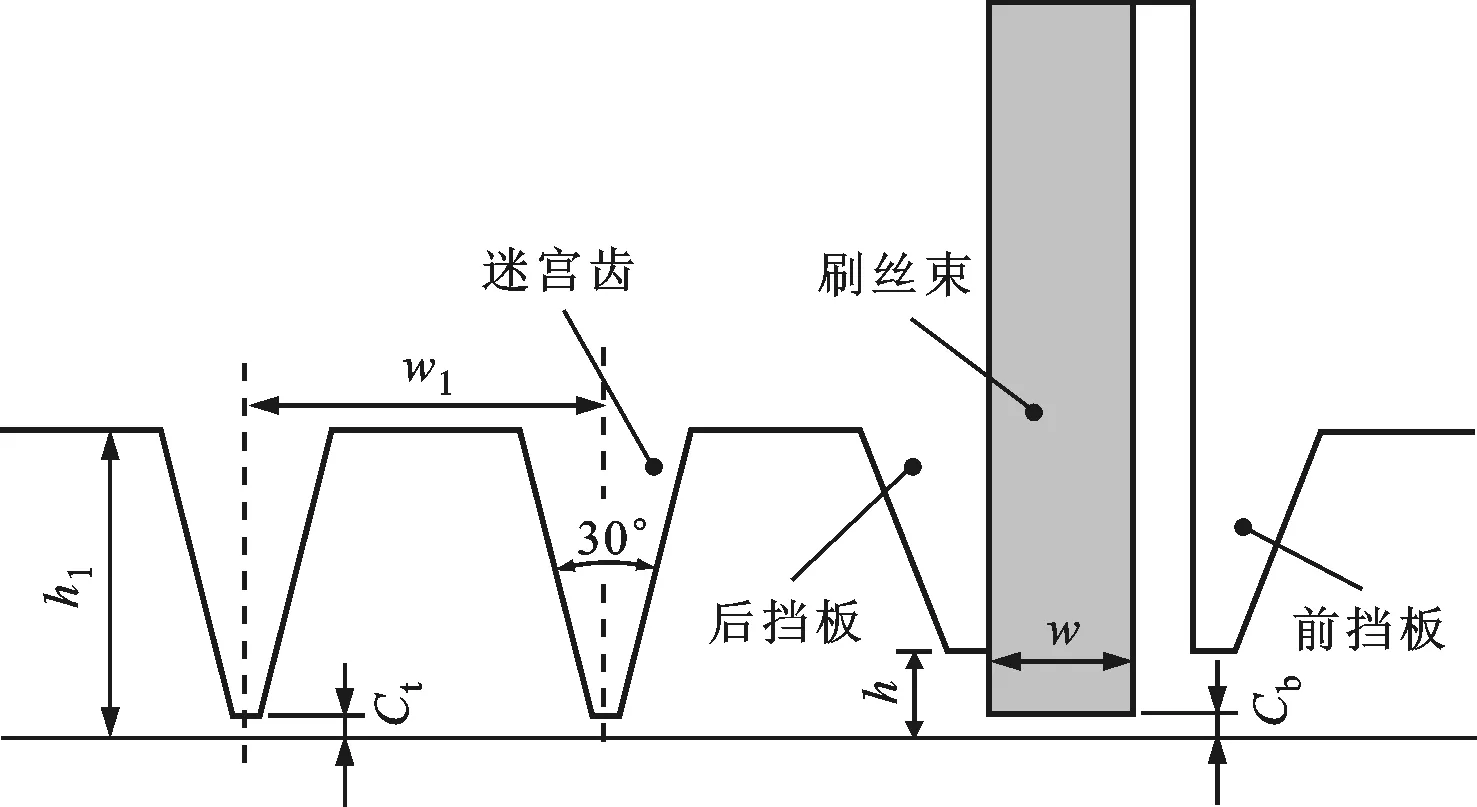
图1 刷式-迷宫密封结构示意图

1 计算模型和数值方法

1.1 计算模型

图1给出了本文所研究的刷式-迷宫密封几何结构图[13]。刷式-迷宫密封结构是将迷宫密封的上游第一个迷宫齿设计为刷丝束,表1给出了刷式-迷宫密封几何参数。由于转子存在涡动位移,数值预测刷式-迷宫密封的气流激振力需要整周360°模型进行计算。图2给出了数值研究刷式-迷宫密封转子动力特性系数的计算网格,上下游进行了适当延伸以保证流动充分。网格的节点总数大约为787万,满足网格无关性和SST紊流模型对y+的要求。

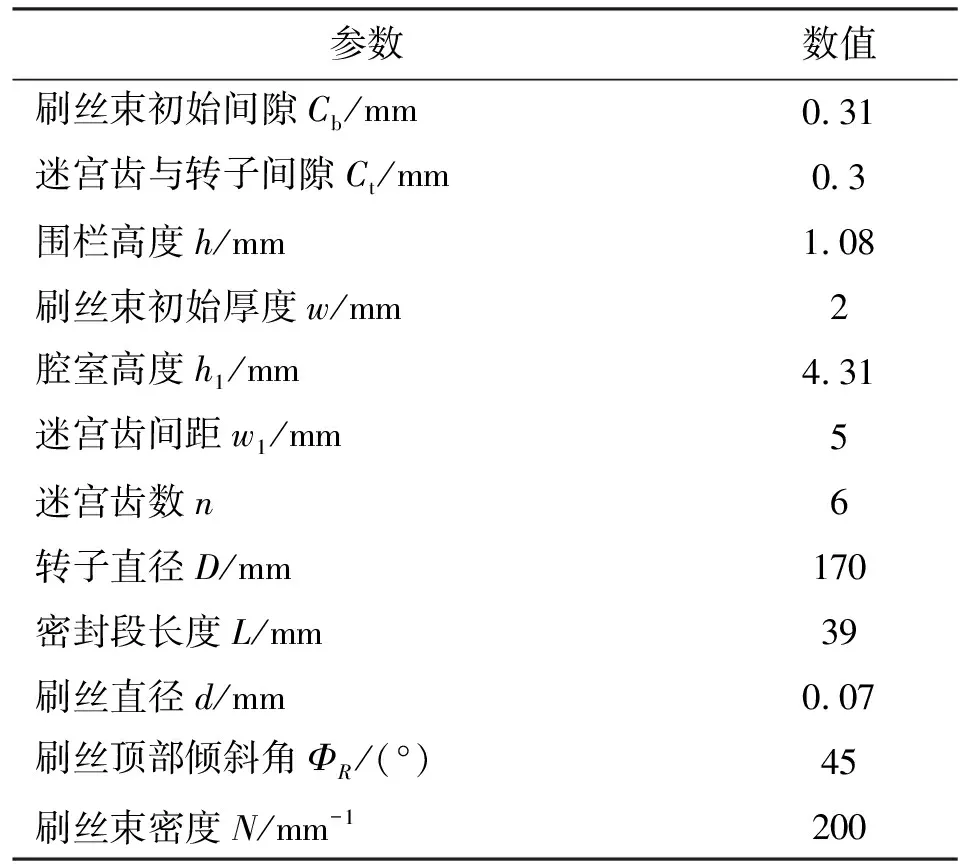
表1 刷式-迷宫密封几何参数

图2 刷式-迷宫密封转子动力特性系数的计算网格

1.2 涡动转子法

(a)静止坐标系瞬态分析 (b)旋转坐标系稳态分析图3 密封转子动力特性计算的涡动转子法

图3给出了密封转子动力特性系数计算的涡动转子法模型,图中o为转子涡动中心,o′为转子自旋中心。由图3a可知,在静止坐标系下,假设转子绕转子中心以速度ω自旋,同时绕静子中心沿圆形轨迹以速度Ω旋转,由于计算区域发生变化,需采用瞬态分析方法求解密封内部流场。对于刷式-迷宫密封结构,密封静子为轴对称光滑旋转面结构的旋转密封,可采用涡动转子法(三维稳态CFD预测模型)将静止坐标系下的非稳态转子涡动问题转化为一个旋转坐标系下转子偏心自旋的稳态问题。由图3b可知,在旋转坐标系下(附在转子轴心上),转子在偏心位置绕转子中心自旋,静子绕静子中心自旋(与转子涡动方向相反),由于计算区域不变,可采用稳态分析方法求解密封内部流场。目前,涡动转子法已被应用于迷宫密封[14]、刷式密封[8,10]、刷式-迷宫密封[2,9]的转子动力特性系数的数值预测中。

(1)

式中:K为直接刚度;k为交叉刚度;C为直接阻尼;c为交叉阻尼。

假设转子绕圆心做圆周涡动,可采用径向力Fr和切向力Ft来衡量流体激振力,即

Fz/e=Fr/e=-K-cΩ

(2)

Fy/e=Ft/e=k-CΩ

(3)

式中:e为涡动半径;Ω为涡动速度。C、k影响转子系统的稳定性,K、c对转子系统的稳定性影响较小,但会显著影响转子系统的固有频率和临界转速,负的直接刚度会使转子系统的临界转速变小。

1.3 多孔介质模型

刷丝束由排列紧密的纤细刷丝层构成,气流在压差作用下通过刷丝间的微小间隙,但其流态十分复杂,直接求解基于真实几何结构的刷封流场非常困难。研究发现,刷丝束内部的流动状态与多孔介质内的流动类似,因此采用多孔介质模型模拟刷丝束内部的流动。本文采用非线性Darcian模型,在动量方程中引入黏性、惯性损失,即

(4)

Fi=-Aijμui-0.5Bijρ|u|ui

(5)

式中:Aij为黏性阻力系数矩阵;Bij为惯性阻力系数矩阵。文献[5]推导得到各方向的阻力系数

(6)

(7)

式中:a,b分别为黏性、惯性阻力系数;下标z、m、n分别为与转轴平行、转子横截面内与刷丝平行、与刷丝垂直的方向。孔隙率是指多孔介质中空隙体积与总体积之比,即

(8)

Φr=arccos(Rcos(ΦR)/r)

(9)

式中:N为刷丝密度;D为密封直径;wb为刷丝束厚度;Φr为刷丝与切向夹角;R为刷丝焊接点处半径;ΦR为刷丝焊接点处刷丝与切向夹角;r为沿径向刷丝各位置点到转子中心的距离。

多孔介质模型中,刷丝束厚度wb随刷丝束上下游压差的变化而显著变化,其值小于刷丝束初始厚度w,刷丝束与转子间隙c因为闭合效应而减小。

1.4 边界条件

基于涡动转子法和非线性Darcian多孔介质模型,采用ANSYS-CFX数值求解三维Reynolds-Averaged Navier-Stokes(RANS)和SST两方程,对刷式-迷宫密封的泄漏流动和转子动力特性进行了研究。表2给出了计算边界条件,其中进口给定总压、总温及流向,正进口预旋表示预旋速度方向和转速方向一致,负进口预旋则表明预旋速度方向和转速方向相反,出口给定静压,工质为理想空气,按照涡动转子法设置转子面、静子面及流体域转速,所有固壁面均设置为绝热壁面。

表2 计算边界条件

(a)有效间隙

(b)直接刚度和交叉刚度图4 刷式-迷宫密封刚度系数的计算值与实验值对比

1.5 数值方法有效性验证

本文采用文献[2]中刷式-迷宫密封的实验结果来验证本文数值方法的有效性,文献[2,15]中数值结果的比较如图4所示。由图4可知,密封有效间隙[13]heff和刚度在各压差下的数值预测值与实验值吻合。直接阻尼被低估,这可能是未考虑转子与刷丝束的接触[9],本文采用的涡动半径小于刷丝束与转子的间隙,不会产生接触。

2 结果与讨论

2.1 有效间隙与流场

密封有效间隙定义为

(10)

(11)

否则

(12)

图5给出了刷式-迷宫密封和作为对比的迷宫密封有效间隙heff随转速和压比的变化曲线。由图5a可知:迷宫密封有效间隙随着压比升高而升高,而刷式-迷宫密封则随着压比升高而降低;随着压比增大,闭合效应使得刷丝束与转子间隙减小,因而刷式-迷宫密封的有效间隙减小。由图5b可知:两种密封的有效间隙均随着转速升高而略微降低,但整体变化不大;刷式-迷宫密封的封严性能显著优于迷宫密封,在压比为6.9时,其有效间隙仅为迷宫密封的25.5%。

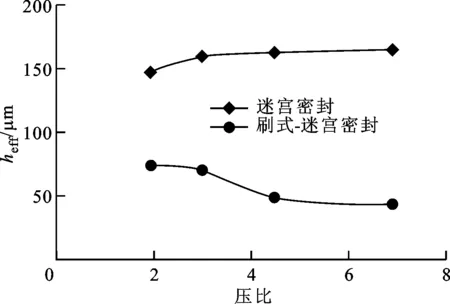
(a)有效间隙随压比变化(ω=15 000 r/min)

(b)有效间隙随转速变化(Rp=6.9)图5 两种密封有效间隙随运行工况的变化曲线(cu0=30 m/s,Ω=0)

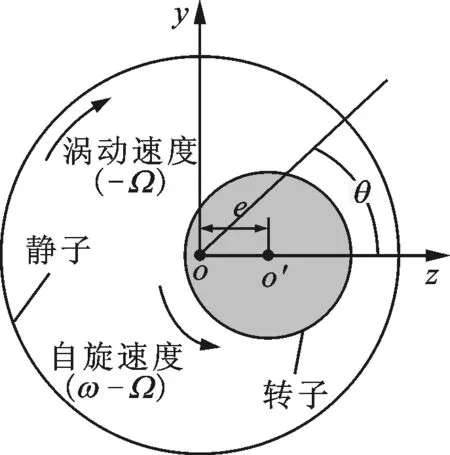
图6 流道截面位置示意图

(a)刷式-迷宫密封

流道截面位置示意图如图6所示,θ=0°时表示转子面与静子面距离最近,θ=180°时表示转子面与静子面距离最远。由图6可知,由于偏心,刷式-迷宫密封的刷丝束靠近转子区域在θ=0°,180°时的速度场存在明显差异:相对θ=0°,θ=180°时的刷丝束与转子间隙较大,流体从缺乏刷丝阻滞的间隙流过,流速较大。对于迷宫密封,转子涡动半径e相对迷宫齿与转子间隙很小,θ=0°,180°时的速度场差异很小。转子偏心运动使得流场沿周向不均,进而产生密封气流激振力,压比为6.9时,刷式-迷宫密封和迷宫密封不同截面的速度云图如图7所示。

(b)迷宫密封图7 刷式-迷宫密封和迷宫密封不同截面的速度云图(Rp=6.9,cu0=30 m/s,Ω=0,ω=15 000 r/min)

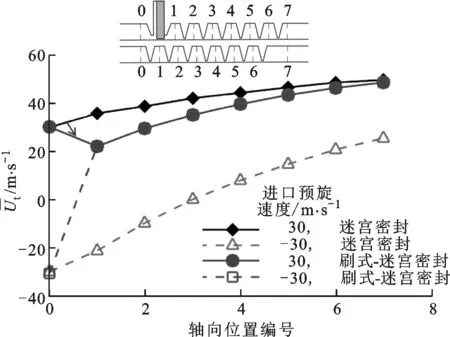
图8 刷式-迷宫和迷宫密封周向平均切向速度沿轴向的分布

2.2 转子动力特性系数

图9给出了刷式-迷宫密封直接刚度K和交叉刚度k随进出口压比的变化曲线。由图9可知,刚度K、k均随着压比的增大而增大,且K增大的速率更快。

图9 刷式-迷宫密封刚度随压比的变化曲线(cu0=30 m/s,ω=15 000 r/min)

进口预旋速度会显著影响密封的转子动力特性,刷式-迷宫密封和迷宫密封转子动力特性系数随进口预旋速度的变化曲线如图10所示。有效阻尼综合考量了交叉刚度和直接阻尼对转子系统稳定性的影响,有效阻尼定义为

Ceff=C-k/Ω

(13)

由图10a可知,进口预旋速度对刷式-迷宫密封直接刚度K的影响与迷宫密封相反,刷式-迷宫密封的K随着进口预旋速度绝对值的增大而增大,迷宫密封的K均随着进口预旋速度绝对值的增大而减小。刷式-迷宫密封和迷宫密封的k均会随着进口预旋速度由负向预旋转变到正向预旋的过程而增大,在正向预旋速度较大时,两种密封的k均为正值,将会产生与转子转动方向相同的切向力,不利于转子系统的稳定。相比迷宫密封,刷式-迷宫密封的k对进口预旋速度的敏感程度更低,即负向预旋速度较大时,迷宫密封的k比刷式-迷宫密封的更小,而正向预旋速度较大时,则刷式-迷宫密封的k更大。由图10b可知,进口预旋速度对刷式-迷宫和迷宫密封直接阻尼C的影响类似,均随着进口预旋速度绝对值的增大而增大,且迷宫密封的直接阻尼C更大,交叉阻尼c随进口预旋变化存在波动,但整体上c的值很小。由图10c可知,进口预旋速度对刷式-迷宫和迷宫密封有效阻尼Ceff的影响类似,均随着进口预旋速度由负向预旋转变到正向预旋的过程中而减小,但进口预旋速度变化对迷宫密封有效阻尼的影响更明显,即刷式-迷宫密封的有效阻尼对转子自旋速度变化的敏感程度更低。在高正向进口预旋速度工况下,刷丝束的止旋作用可降低密封流道内的正切向速度,使得有效阻尼增大,转子稳定性增强。在负预旋工况下,刷丝束的止旋作用会减弱负预旋带来的稳定性。

(a)直接刚度和交叉刚度

(b)直接阻尼和交叉阻尼

(c)有效阻尼图10 进口预旋速度对密封转子动力特性系数的影响(Rp=6.9,ω=15 000 r/min)

(a)直接刚度和交叉刚度

(b)直接阻尼和交叉阻尼

(c)有效阻尼图11 转子自旋速度对密封转子动力特性系数的影响(Rp=6.9,cu0=30 m/s)

转子自旋会导致气流周向旋转,进而影响密封的转子动力特性,刷式-迷宫密封和迷宫密封转子动力特性系数随转子自旋速度的变化曲线如图11所示。由图11a可知:转子自旋速度对刷式-迷宫密封直接刚度K的影响很小,而迷宫密封K随着转子自旋速度绝对值的增大而略微减小,且在研究工况范围内刷式-迷宫密封的K显著大于迷宫密封的直接刚度,K越大则转子从偏心位置向静子中心移动的趋势越大;转子自旋速度对刷式-迷宫密封交叉刚度k的影响与迷宫密封刚好相反。随着转速升高,迷宫密封的k显著减小,而刷式-迷宫密封的k则增大,但整体变化不大,即刷式-迷宫密封k对转子自旋速度变化的敏感程度更低。由图11c可知:转子自旋速度对两种密封直接阻尼C和交叉阻尼c的影响类似,转子自旋速度增大使得C、c均减小,但整体上转子自旋速度变化对两种密封的C、c的影响很小;转子自旋速度对两种密封有效阻尼的影响相反,随着转子自旋速度增大,迷宫密封的有效阻尼增大,而刷式-迷宫密封的有效阻尼则减小,且转子自旋速度对刷式-迷宫密封有效阻尼的影响程度小于迷宫密封,即刷式-迷宫密封的有效阻尼对转子自旋速度变化的敏感程度更低。转子自旋速度较低时,刷式-迷宫密封的有效阻尼明显大于迷宫密封,转子自旋速度较大时,迷宫密封的有效阻尼大于刷式-迷宫密封的。

3 结 论

本文基于涡动转子法和非线性Darcian多孔介质模型,建立了刷式-迷宫密封泄漏流动和转子动力特性系数数值预测模型,研究了压比、进口预旋速度、转子自旋速度对刷式-迷宫密封泄漏特性和转子动力特性的影响,并与迷宫密封进行了比较,得到如下结论。

(1)刷式-迷宫密封的封严性能显著优于迷宫密封的,且两者的有效间隙均随着转速的升高而略微降低,但整体影响不大。

(2)刷式-迷宫密封的直接刚度随进出口压比和进口预旋绝对值的增大而增大,随转子自旋速度改变变化不明显,有效阻尼随进口预旋速度和转子自旋速度的升高而降低。

(3)相比迷宫密封,刷式-迷宫密封的交叉刚度和有效阻尼对运行工况变化敏感度更低。刷式-迷宫密封的直接刚度在研究工况范围内均大于迷宫密封的,临界转速更高。刷丝束有止旋的作用,在相同工况条件下,正向预旋速度较大和转子自旋速度较低时,刷式-迷宫密封有效阻尼大于迷宫密封的,转子系统稳定性更好。

综上所述,进口预旋速度和转子自旋速度对刷式-迷宫密封和迷宫密封的转子动力特性有显著影响,且对刷式-迷宫和迷宫密封的影响规律不同,但刷式-迷宫密封的封严性能更优。