自由分子流区气体外掠平板/圆柱体流动与传热预测

谢福寿,雷刚,徐元元,陈强,邱一男,厉彦忠

(1.西安交通大学能源与动力工程学院,710049,西安;2.航天低温推进剂技术国家重点实验室,100028,北京)

随着航天事业大力发展,自由分子流区稀薄气体流动与传热问题日益受到人们的关注。在轨卫星姿态调整时,自由分子流作用在飞行器上的气动力非常显著[1];运载火箭升空时,随着大气密度的逐渐减小,气体的稀薄效应开始凸显,连续介质假设逐渐失效,此时气体流态会依次经历连续流区(Kn<10-2)、滑移流区(10-210)[2-5]。自由分子流区中气体分子与物体间的碰撞相比较,分子之间的碰撞可以忽略,此时可采用平衡Maxwell分布函数对Boltzmann方程进行求解,从而获得预测物体阻力和传热规律的解析解。

虽然许多学者推导了自由分子流传热与流动的量纲表达式[6-12],但都没有进一步深入分析雷诺数Re、马赫数Ma和克努森数Kn对流动与传热特性的影响,且推导的过程要么过于复杂,要么表达式直接给出,考虑到物理本质的内在简单性,其计算也简单化。为了进一步理解自由分子流传热与流动特性,本文拟采用相对坐标系思想来重新推导预测典型几何尺寸传热与流动的表达式,并详细阐述推导的每一个过程,使其更容易被理解。在此基础上,通过一系列物理量变换,将原表达式中含有的微观量纲参数全部转化为无量纲表达式,从而反映出无量纲参数之间本质变化规律,建立努塞尔数与克努森数、雷诺数、马赫数之间的关系,并探讨阻力和传热性能的影响因素,以便应用于实际工程预测之中。

1 数学表达式推导

1.1 大气外掠平板传热

平板以一定攻角穿过处于自由分子流区的大气层时,可视为大气以一定速度u∞外掠平板,T∞为远离平板的温度,Tw为平板壁面的温度,θ为来流速度与平板壁面的夹角,dA为单位面积,外掠平板的示意图如图1所示。

图1 气体外掠平板的示意图

由于自由分子流中分子与分子之间的碰撞可忽略,故可将Boltzmann方程的碰撞项简化为0,从而导出平衡气体分子的Maxwell速度分布函数为

(1)

假设沿着坐标系(x′,y′,z′)以Ux、Uy、Uz宏观速度运动,而将观察者自身作为一个移动的相对坐标系(x,y,z),并以此作为一个新参考系,此时在x、y、z向的相对分子速度(分子热运动)为

(2)

在相对参考坐标系中,可认为观察到的气体仍然是平衡气体,不存在速度和温度梯度,则气体分子的相对速度符合Maxwell分布,流动气体的Maxwell分布为

(3)

为了得到单位时间单位面积上入射于壁面的分子通量φ,可对ux从-∞到0、uy从-∞到∞、uz从-∞到∞积分。由于在x向正速度的气体分子不会穿过平板壁面,所以积分上限为0,即

(4)

(5)

根据式(3),可将入射于微元表面的气体分子速度分布函数表示为

(6)

假定气体分子在表面发生完全漫反射,则气体分子反射出的速度分布函数为

(7)

式中:ψ为入射于微元dA上的分子通量;T为漫反射分子的温度,K。

大气中每一个分子携带的能量e可表示为

(8)

式中:v为单个分子速度,m·s-1;m为单个分子的质量,kg;ε为分子内部能量,J。

根据Maxwell方程求矩思想,单位时间单位面积上大气分子入射于平板壁面时携带的能量为

(9)

平板壁面漫反射的大气分子所携带能量为

ψ(2kT+εout)

(10)

在平板壁面任意取一个微元表面dA为研究对象,由于能量守恒,故微元表面dA上的热量为

Q=(Ein-Eout)dA

(11)

式中:Ein为在单位面积上入射于平板表面的气体分子携带的能量,J;Eout为在单位面积上从表面反射分子所携带的能量,J。

于是单位面积上的热流密度可表示为

q=Ein-Eout

(12)

将式(9)(10)代入式(12),则单位面积上的热流密度可化解为

ψ(εin-εout-2kT)

(13)

(14)

(15)

(16)

根据理想气体状态方程p∞=nkT∞和式(5),式(13)可简化为

(17)

为了消除未知量T,可借鉴Smoluchowski和克努森引用热协调系数的方法,进一步改写式(17)。热协调系数定义为

(18)

式中:Ew为对应于壁面温度Tw的麦克斯韦分布时所应带走的能量通量。σT的数值大小表示入射的气体分子和壁面之间能量交换的完善程度。式(17)可改写为

(19)

(20)

(21)

式中:M为摩尔质量,kg/mol;NA为阿伏伽德罗常量。玻尔兹曼常量定义为

(22)

(23)

p∞=ρRgT∞

(24)

式中:R=8.314 J/(mol·K)为通用气体常数。

牛顿冷却定律可表达为

q=h(T∞-Tw)

(25)

比定压热容可表示为

(26)

(27)

根据努塞尔数定义Nu=hD/λ,普朗特数定义Pr=μcp/λ和克努森数定义Kn=Lm/D,可导出

(28)

式中Tw为壁面温度。

1.2 大气外掠平板的阻力

依据空气动力学可知,作用在平板微元上的曳力可分解成与平板表面垂直的压力p和与平板表面水平的剪切力τw,阻力可表示为

dFD=-pdAsinθ+τwdAcosθ

(29)

大气与平板表面的压力和剪切力可视为入射分子与反射分子与表面相互作用而产生的,可分别表示为

p=pin+pout

(30)

τw=τw_in+τw_out=

τw_in_xv+τw_in_xz+τw_out_xy+τw_out_xz

(31)

式中:pin为入射分子通量的法向动量;pout为入射反射分子通量的法向动量;τw_in为入射分子通量的切向动量,由于在z向上分子没有宏观速度,此时分子热运动产生的切向力为大小相等方向相反的力,即τw_in_xz=0;τw_out为反射分子通量的切向动量,由于反射分子在y、z向上分子没有宏观速度,则τw_out_xy=0,τw_in_xz=0。

与传热一样,为表述反射分子通量切向和法向分力,引入两个动量协调系数

(32)

(33)

式中:στ为切向动量协调系数;τw_w为小于Tw的分子切向动量,值为0;σp为法向动量协调系数;pw为分子法向动量。

在微观系统中,宏观参数压力和剪切力是大气分子与平板壁面的动量交换而产生的。假设大气分子在平板壁面上发生完全漫反射,即大气分子速度分布符合Maxwell分布函数。根据Maxwell方程求矩思想,采用相对坐标系方法可得到单位时间单位面积上大气分子作用于平板壁面上的各个力,即

(34)

(35)

将式(34)(35)代入式(29),可得平板表面微元上曳力

(36)

阻力系数定义为

(37)

气体声速计算式为

(38)

将式(20)(37)(38)代入式(36),可得

(39)

1.3 大气外掠圆柱体的传热

当一个无限长、半径为r的圆柱体垂直放置于气流中时,壁面法线方向可视为x坐标,切线方向视为y坐标,壁面法线方向与大气流动方向夹角为θ,大气外掠圆柱体流动的示意图如图2所示。此时,大气横掠圆柱体流动问题可转化为气流以不同的攻角外掠平板表面,得到壁面局部换热性能。在实际工程中,往往关心的是圆柱体壁面平均换热能力,在自由分子流区大气横掠圆柱体的平均努塞尔数可表示为

(40)

将式(19)代入式(40),可得

(41)

其中I0(S2/2)和I1(S2/2)分别为修正的零阶和一阶贝塞尔函数[11]。可得

(42)

图2 大气外掠圆柱体流动的示意图

1.4 大气外掠圆柱体的阻力

与传热计算一样,工程计算中关心的是圆柱体壁面的平均阻力,在自由分子流区大气横掠圆柱体的平均阻力系数可表示为

(43)

根据阻力系数和马赫数定义,将式(36)代入式(43),可得

(44)

2 结果讨论

2.1 大气外掠平板传热

为了进一步讨论高速平板以一定攻角穿过大气层时壁面与大气的换热能力,本文展示了在不同马赫数和克努森数下,平板表面的传热性能随平板攻角的变化曲线。图3给出了平板在克努森数为15、壁面温度为195 K、大气温度为200 K时,努塞尔数随攻角和马赫数的变化。由图3可知,马赫数一定、大气水平掠过平板时,热流密度最低,而垂直入射时热流密度最高,这是因为平板以一定攻角高速升空时,气体压缩效应完全凸显,此时不仅有温差引起的热流,还存在气体动能转化为内热能的热流,当大气垂直入射时,气体动能将全部转化为内热能,如运载火箭顶部整流罩的气动加热现象,且马赫数越高,气动加热越显著。图4给出了平板在马赫数为6、其他条件不变时,努塞尔数随攻角和克努森数的变化曲线。由图4可知,随着克努森数的不断增加,平板壁面与大气的换热能力逐渐下降,不过克努森数越大,传热性能下降速率减弱,这是因为克努森数越大,说明大气越稀薄,其气体分子与平板壁面碰撞频率减小,从而气体分子碰撞后带走能量就越小。图5给出了不同克努森数下零攻角平板传热性能随马赫数的变化。由图5可知,在不同克努森数下,平板以零攻角外掠平板表面时,努塞尔数随马赫数的变化规律,当克努森数一定时,只要马赫数超过0.1,对平板表面的传热能力就有显著影响,且马赫数越大,这种影响越显著,这是因为气体宏观速度足够大,致使大气分子热运动完全可忽略,对流影响占主导地位,而马赫数小于0.1时,其对平板表面的换热影响并不大,因为大气运动可看作不可压缩流体,此时大气分子无规则热运动占主导地位。

图3 不同马赫数下平板传热性能随攻角的变化

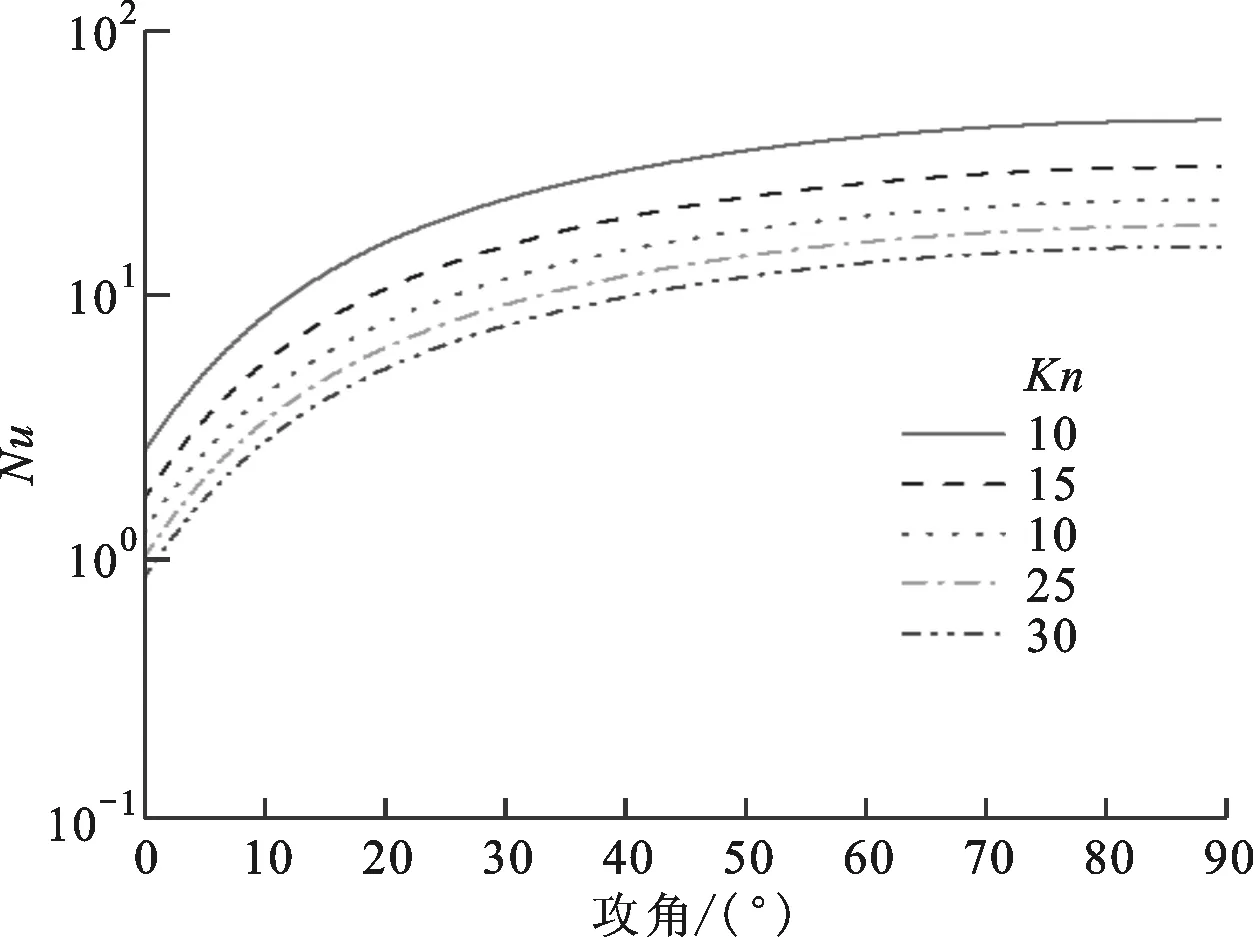
图4 不同克努森数下平板传热性能随平板攻角的变化

图5 不同克努森数下零攻角平板传热性能随马赫数的变化

2.2 大气外掠平板流动

图6给出了大气在不同攻角下外掠平板的阻力系数随马赫数的变化,大气温度为200 K,平板壁面温度为195 K。由图6可知:攻角为0°,即平板表面平行于气流时,平板阻力最小,此时阻力完全由作用于平板壁面上剪切力所决定;随着攻角的增大,平板阻力增加,当攻角为90°即大气速度垂直于平板壁面时,平板阻力最大,此时阻力完全由作用于平板壁面上压力所决定,随着攻角的增加,平板阻力增加的速率逐渐变缓;当攻角一定时,平板阻力系数随着大气来流速度增加而先急剧下降,当达到超声速时,逐渐变缓,最终趋于恒定,这是因为随着来流速度的增加,惯性力开始体现,当到达超声速时,惯性效应完全占主导地位。

图6 不同攻角下平板阻力系数随马赫数的变化

2.3 大气外掠圆柱体传热

为了进一步讨论高速气流以垂直于圆柱体轴线的方向掠过时壁面与大气的换热能力,本文绘制了在不同克努森数下,圆柱体表面的传热性能随马赫数的变化曲线,如图7所示。由图7可知:当克努森数一定、马赫数小于0.1时,所对应的平均努塞尔数基本保持不变;马赫数大于0.1时,平均努塞尔数会随着马赫数增加而急剧升高,这是因为高速气流的压缩影响完全体现出来;当马赫数一定时,平均努塞尔数会随着克努森数增加而下降,且下降速率会逐渐减弱,这是因为气体变得更稀薄,大气分子与圆柱体壁面碰撞概率大大降低。

图7 不同克努森数下圆柱体换热随马赫数的变化

2.4 大气外掠圆柱体流动

图8给出了大气在自由分子流区横掠圆柱体的平均阻力情况,大气温度为200 K,平板壁面温度为195 K。由图8可知:阻力系数与大气外掠平板的情况相一致,即在最小马赫数下对应最大的阻力系数,随着马赫数的增加,阻力系数先急剧下降,当达到超声速时,阻力系数逐渐变缓。

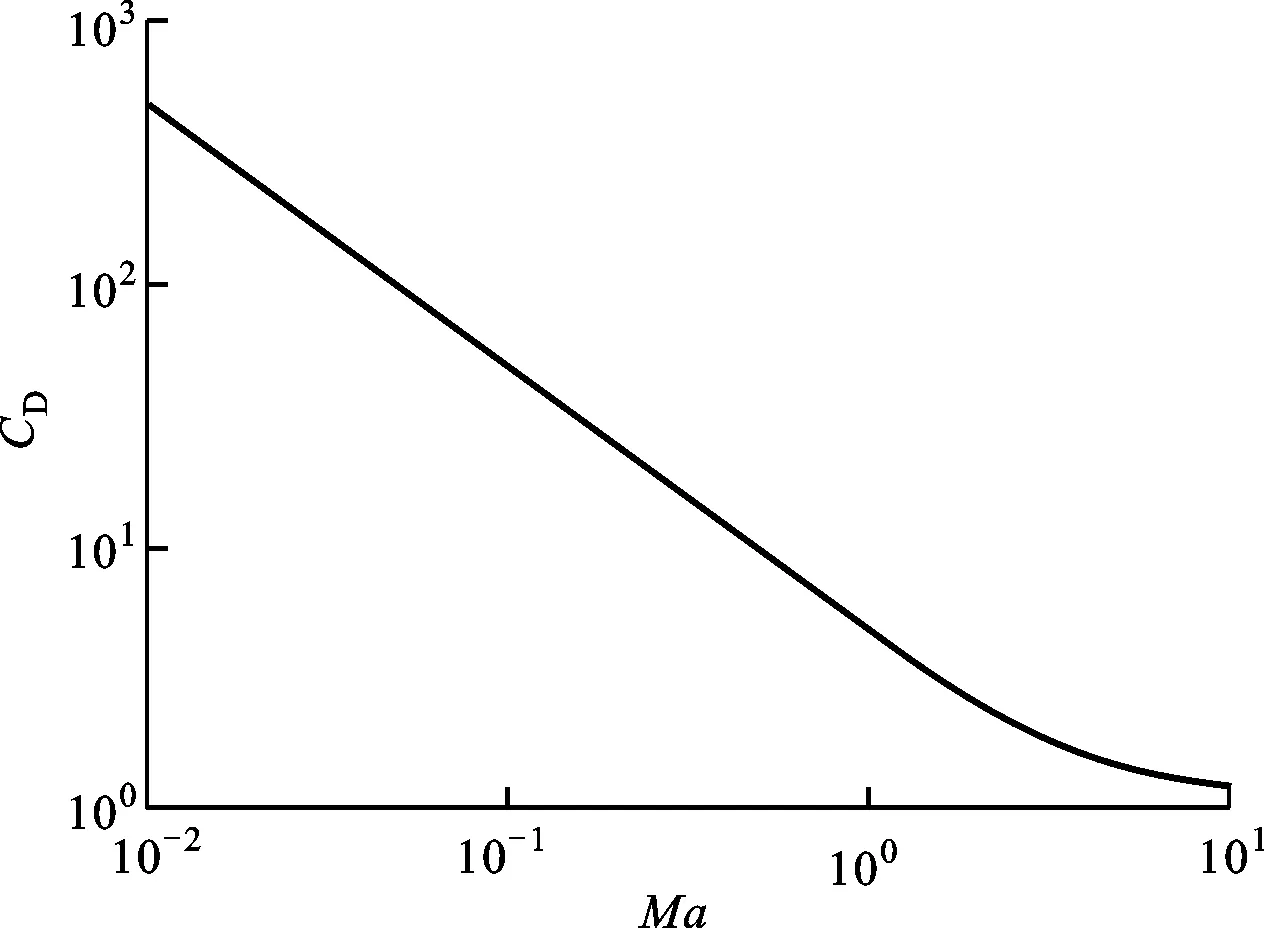
图8 自由分子流区外掠圆柱体的阻力系数

3 结 论

(1)在马赫数一定时,大气水平掠过平板所对应的热流密度最低,而垂直入射时热流密度最高。随着克努森数的不断增加,平板壁面与大气的换热能力逐渐下降,传热性能下降速率减弱。

(2)当克努森数一定时,只要马赫数超过0.1,对平板表面的传热能力就有显著影响,且马赫数越大,这种影响越显著;马赫数小于0.1时,对平板表面的换热影响并不大。

(3)当攻角为0°即平板表面平行于气流时,平板阻力最小,此时阻力完全由作用于平板壁面上剪切力所决定。随着攻角的增大,平板阻力增加,当攻角为90°,即大气速度垂直于平板壁面时,平板阻力最大。随着攻角的增加,平板阻力增加的速率逐渐变缓。当攻角一定时,平板阻力系数随着大气来流速度增加而急剧下降,当达到超声速时逐渐变缓,最终达到一个恒定值。

(4)当克努森数一定时,马赫数小于0.1所对应的大气横掠圆柱体平均努塞尔数基本保持不变,但一旦马赫数超过0.1,平均努塞尔数会随着马赫数增加而急剧升高。然而,当马赫数一定时,平均努塞尔数会随着克努森数增加而下降,且下降速率会逐渐减弱。

(5)大气外掠物体的流动阻力仅与马赫数、比热容比、壁面温度和来流温度有关,与稀薄效应无关。气体外掠圆柱体时,在最小马赫数下对应最大的阻力系数,随着马赫数的增加,阻力系数先急剧下降,当达到超声速时,阻力系数逐渐变缓。