离散GM(1,1)模型在服装流行色预测中的应用
周 捷,李 健
(西安工程大学 服装与艺术设计学院,陕西 西安 710048)
0 引 言
服装流行色是社会心理学的产物,反映了人们相互之间的共同审美[1]。流行色作为一个突发性和不确定性的复杂系统,不仅受到穿着者肤色、体型、性格和心理等内部因素影响,还受到外部因素(包括地理位置、政治、经济、文化背景、科技进步、明星效应等)的影响,如何准确量化和预测色彩成为一道难题。迄今,相当多的学者从事服装色彩量化预测的数学建模,主要方法有基本统计分析法[2-3]、回归分析[4]、灰色理论[5-6]、BP神经网络[7-8]、灰色神经网络[9-10]等。这些研究成果为定量预测服装流行色提供了有益的启示,但其预测性能仍有待提高。
由于受到众多影响因素的干扰,服装流行色往往出现较大的波动,并表现出极大的不确定性。该系统可用于建模的特征数据序列较少,传统统计方法很难做出合理的预测。在众多方法中,灰色GM(1,1)模型[11-12]对解决数据量少、信息不确定性系统具有天然优势,可应用于服装流行色的预测中。但是,常规GM(1,1)模型对波动数据时间序列的预测效果并不理想,需要进一步优化。离散GM(1,1)模型(DGM)采用离散形式对GM(1,1)模型进行了改进,可以看作是GM(1,1)模型的精确形式[13]。基于此,本文根据中国纺织信息中心发布的2013—2019年春夏流行色定案,以HSV色彩体系为色彩量化依据,建立DGM(1,1)流行色趋势预测模型。同时,将预测结果与常规GM(1,1)模型(EGM)、原始差分GM(1,1)模型(ODGM)和均值差分GM(1,1)模型(EDGM)进行比较,探讨GM(1,1)模型的4种基本形式及其适用范围,旨在为合理选择和运用灰色模型预测服装流行色时提供参考依据。
1 材料与方法
1.1 数据来源
依据流行色的7年周期理论[14],以中国纺织信息中心发布的2013—2019年春夏流行色定案为研究对象,收集其对应的CNCS(中国色彩标准体系)色彩编号。经数据预处理,剔除了缺少色彩编号的5个金属色和1个渐变色样本,最终共得到260个流行色定案。
1.2 色彩量化
色彩量化一般借助色彩处理软件实现,取色并转化为计算机色彩体系(RGB)。在RGB色彩体系中,R、G、B分量会被分配0~255之间的灰度值,共产生2563=16 581 375种颜色,极大地增加了计算的复杂性。相比而言,HSV色彩体系以色相(H)、纯度(S)、明度(V)量化表征色彩,更接近于人眼视力对色彩的感知[15],因此本文采用HSV色彩体系作为色彩量化依据。
依据相关色彩理论[16],采用(6∶5∶5)非均匀量化方案进行区间划分,降低量化指标的复杂度。为此,将色相(H)量化为6级,纯度(S)和明度(V)分别量化5级。量化结果为

(1)

(2)

(3)
量化完成后,把色彩S、V分量映射到H轴方向,见图1。图1中R,G,B,Y,C,Cy,W分别表示红色、绿色、蓝色、黄色、青色、品红色、白色等色彩值在H轴的投影分量。使3种颜色分量合成一维特征矢量[17],这样H、S、V等3个分量就在一维矢量上分布开来。即
L=HQSQV+SQV+V
(4)
式中:QS和QV分别表示S和V的量化级数。由式(2)和式(3)可知,QS=5,QV=5,则式(4)表示为L=25H+5S+V。这意味着,本文建立了一种以H为主、V和S为辅的服装色彩量化方法,且H、V和S的权重依次为25,5和1。由于在HSV空间,色相是色彩的基本属性,而明度和纯度影响色彩的明暗和深浅,因此,色彩值主要由H分量来决定,S和V分量对色彩整体影响较小。该方法能有效降低亮度等外部属性的影响,为数字化色彩构建及服装图像检索提供了新思路。
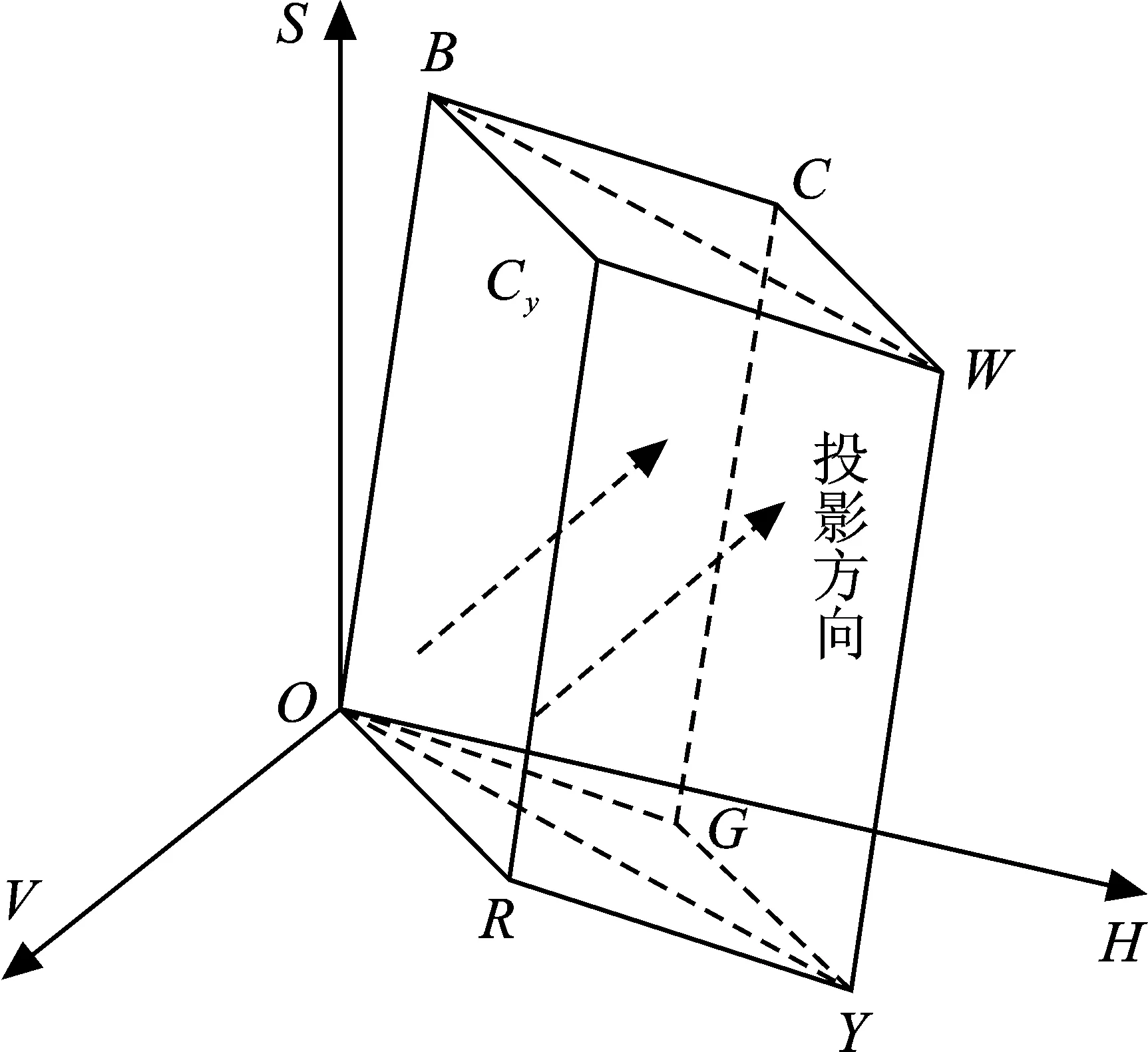
图 1 3个颜色分量投影图
1.3 色彩转换
为便于流行色的量化分析,需将其转化为连续、权威、大众化的数字色彩。通过CNCSCOLOR色彩配方数据库和计算机HSV色彩对色卡信息进行色彩转换。以R、G、B分别表示红、绿和蓝色彩系统,H、S、V分别表示色相、纯度和明度,色卡量化步骤见图2。
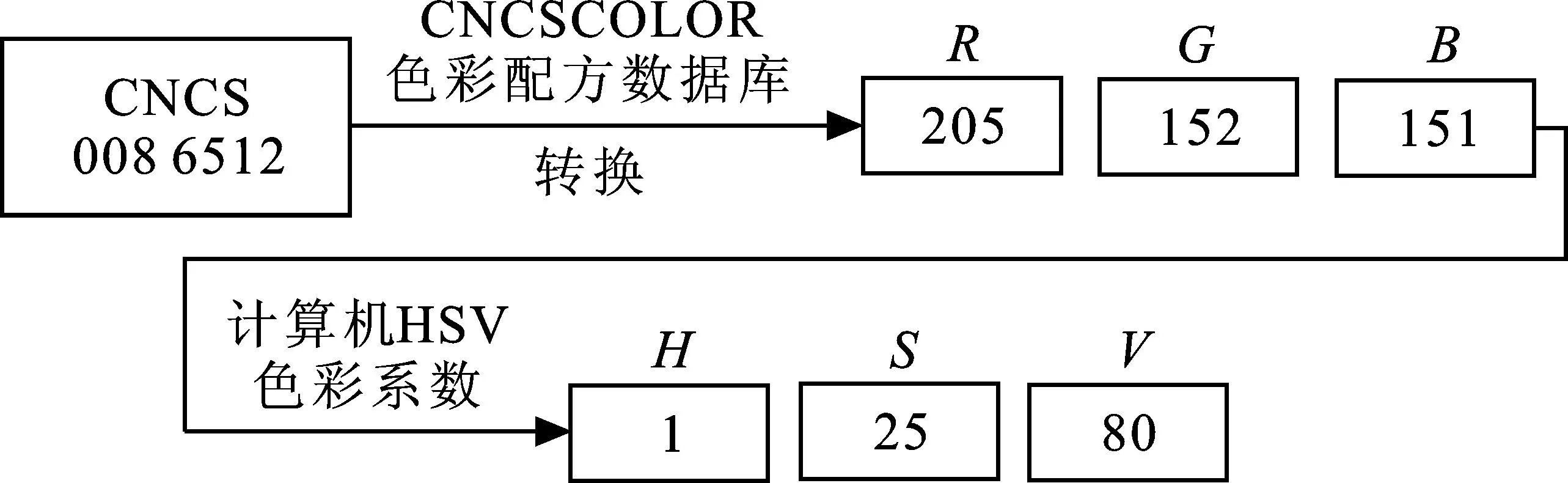
图 2 色卡量化步骤Fig.2 Step of color card quantization
RGB颜色到HSV空间的转换公式[18]为

(6)
式中:V∈[0,1],S∈[0,1],H∈[0,360°]。
以蓝色为例。在HSV色彩系统中,蓝色系在色相上的区间为[210°,270°)。当色相取值越靠近210°,表示色彩中的蓝色因子越少,青色因子越多;反之,越靠近270°,则表示蓝色因子越少,品红色因子越多。中位数计算公式为

(7)
式中:He为中位数;L为中位数组的下限;∑f/2为中位数的位次;Sm-1为中位数组的前一组对应的累计权数;fm为中位数所在组的频数;d为组距。
经色彩转换,得到在HSV色彩体系下的色彩值,见表1。
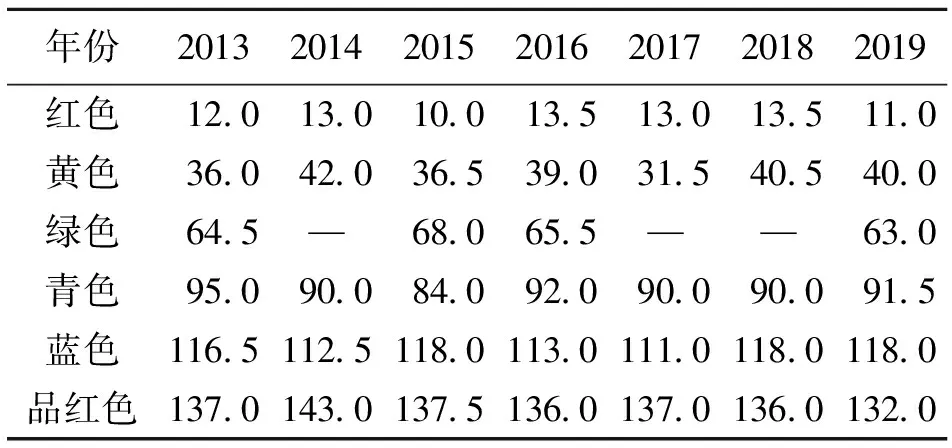
表 1 2013—2019年流行色色彩值
1.4 研究方法
DGM(1,1)模型是以离散形式对GM(1,1)模型进行改进,弥补了常规GM(1,1)模型预测条件的局限性,具有小样本建模、预测精度高的优点[19]。设服装流行色的原始时间序列X(0)构成非负序列,X(0)={x(0)(1),x(0)(2),…,x(0)(n)},DGM(1,1)模型的建立步骤和检验方法详见文献[20-21],在此不再赘述。
2 结果与分析
2.1 色彩特征分析
对2013—2019年服装流行色进行线性趋势分析和滑动平均检验,得到流行色变化趋势线和3年滑动平均曲线(见图3)。应用SPSS 22.0软件统计色彩值数据,得到6类色相的统计特征(见表2)。分析可得:
(1) 线性拟合趋势显示,服装流行色数据的变化增加-降低的波动性显著,但6类色彩的变化程度各异。在趋势减少的色彩中,趋向率排序为绿色>品红色>青色,且均大于0.1,说明这3类色彩的下降趋势显著;在趋势增加的色彩中,趋向率排序为蓝色>黄色>红色,其中蓝色和黄色的趋向率大于0.1,而红色则小于0.1,说明蓝色和黄色的波动较大,红色的变化趋势相对稳定。
(2) 3年滑动平均曲线显示,服装流行色序列趋势波动显著,呈现缓慢的总体上升或下降趋势,这与整体变化趋势基本一致。

(a) 红色 (b) 黄色 (c) 绿色
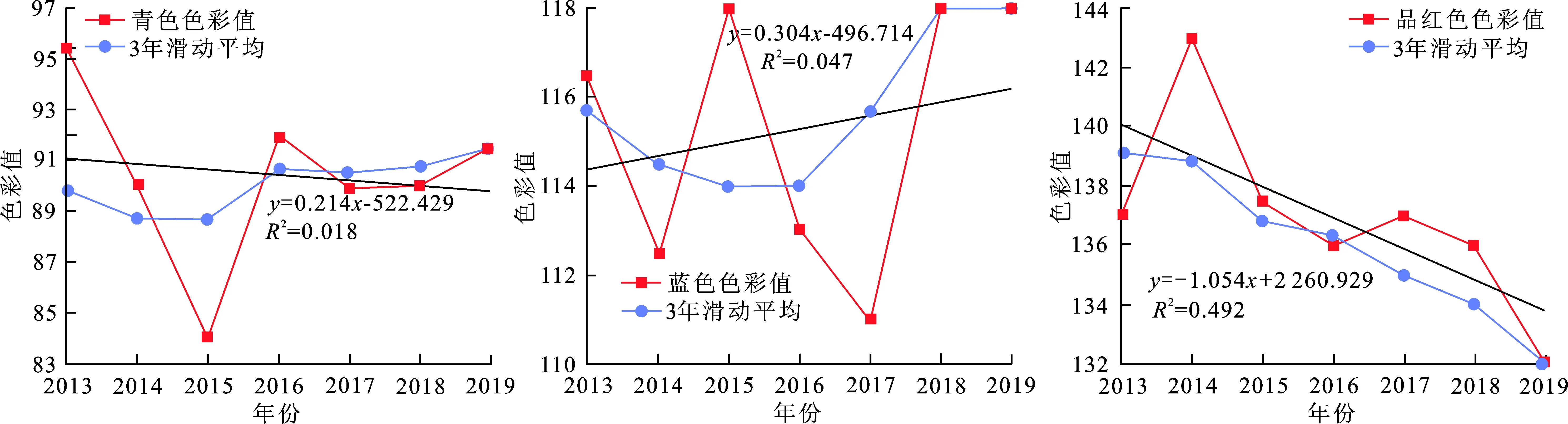
(d) 青色 (b) 蓝色 (c) 品红色图 3 2013—2019年6类色彩变化趋势Fig.3 Six color trends from 2013 to 2019
(3) 定案中变异系数黄色>红色>青色>绿色>品红色>蓝色,说明黄色的离散程度最显著,蓝色波动幅度最小,证实了图3中色彩的变化趋势。
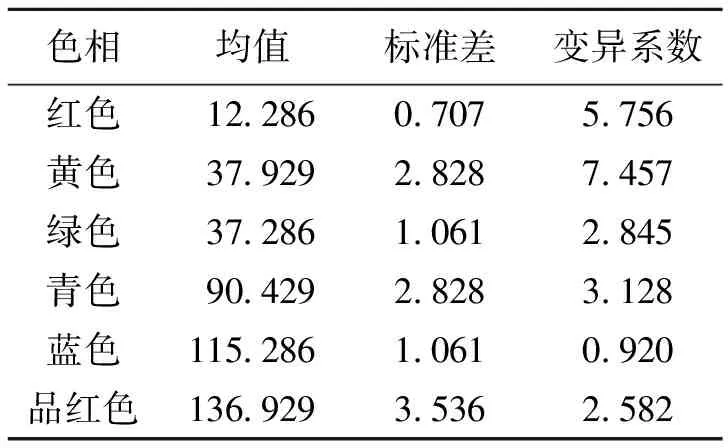
表 2 2013—2019年6类色彩的统计特征
2.2 DGM(1,1)模型建立
以2013—2019年服装流行色值(见表1)为原始序列输入,以DGM(1,1)模型的服装流行色值为输出,并比较仿真值与实际值的误差。由于原始序列至少需要4个数据[22],表1中绿色出现的随机性强,不适合进行灰色建模,故剔除。以蓝色为例,阐述DGM(1,1)模型的建立过程。
由原始序列x(0)(k)=(116.5, 112.5, 118, 113, 111, 118, 118),做1次累加(AGO)生成数列
x(1)(k)= (116.500,229.000,347.000,460.000,
571.000,689.000,807.000)
经计算,得到参数:β1=1.006,β2=43.858,系数x(0)(1)(β1-1)+β2=113.285。
离散GM(1,1)模型的时间响应序列为
115.439,116.166,116.897)
2.3 模型检验

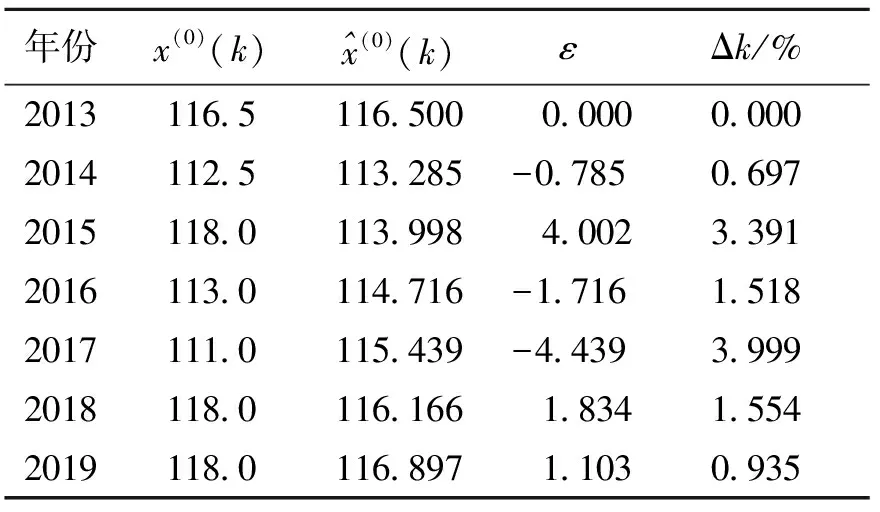
表 3 基于DGM(1,1)模型的蓝色流行色值检验
表3显示,DGM(1,1)模型平均相对误差为2.011%,均方差比值C为0.444 54,小误差概率P大于95%。对比预测精度检验等级[23]可知,DGM(1,1)模型的精度等级为一级,即拟合效果较好,适用于服装流行色预测。
2.4 模型应用
采用DGM(1,1)模型对2020年色彩数据进行预测,结果见表4。由表4可以看出:
(1) 以2013—2019年序列进行建模,除绿色不满足建模条件,其余色彩均符合精度要求;
(2) 2020年红色、黄色将与色彩中位数持平,青色和蓝色将略高于色彩中位数,而品红色将略低于色彩中位数;
(3) 经与历年色彩数据对比,色彩均符合往年波动幅度范围,验证了DGM(1,1)模型预测结果的合理性;
(4) 与2019年相比,2020年红色和青色将会出现稳定增多趋势,而黄色、蓝色和品红色将出现小幅度减少趋势。
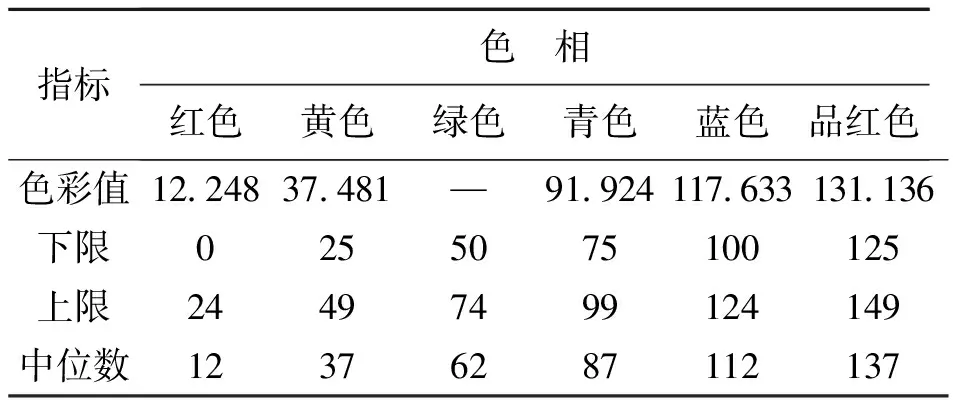
表 4 DGM(1,1)模型对2020年色彩值预测结果
3 讨 论
GM(1,1)模型是最为常见的一种灰色预测模型,在动态非线性变化的系统中拟合度高,预测效果较好。现有研究一般侧重于常规GM(1,1)模型的预测精度[24-25],而对于GM(1,1)模型的4种基本形式及其适用范围,并未深入研究。为探讨服装流行色的最优预测模型,将DGM(1,1)模型的预测结果与GM(1,1)、ODGM(1,1)、EDGM(1,1)模型对比分析。以4种不同序列类型的GM(1,1)模型拟合2013—2019年春夏流行色定案,结果见表5。
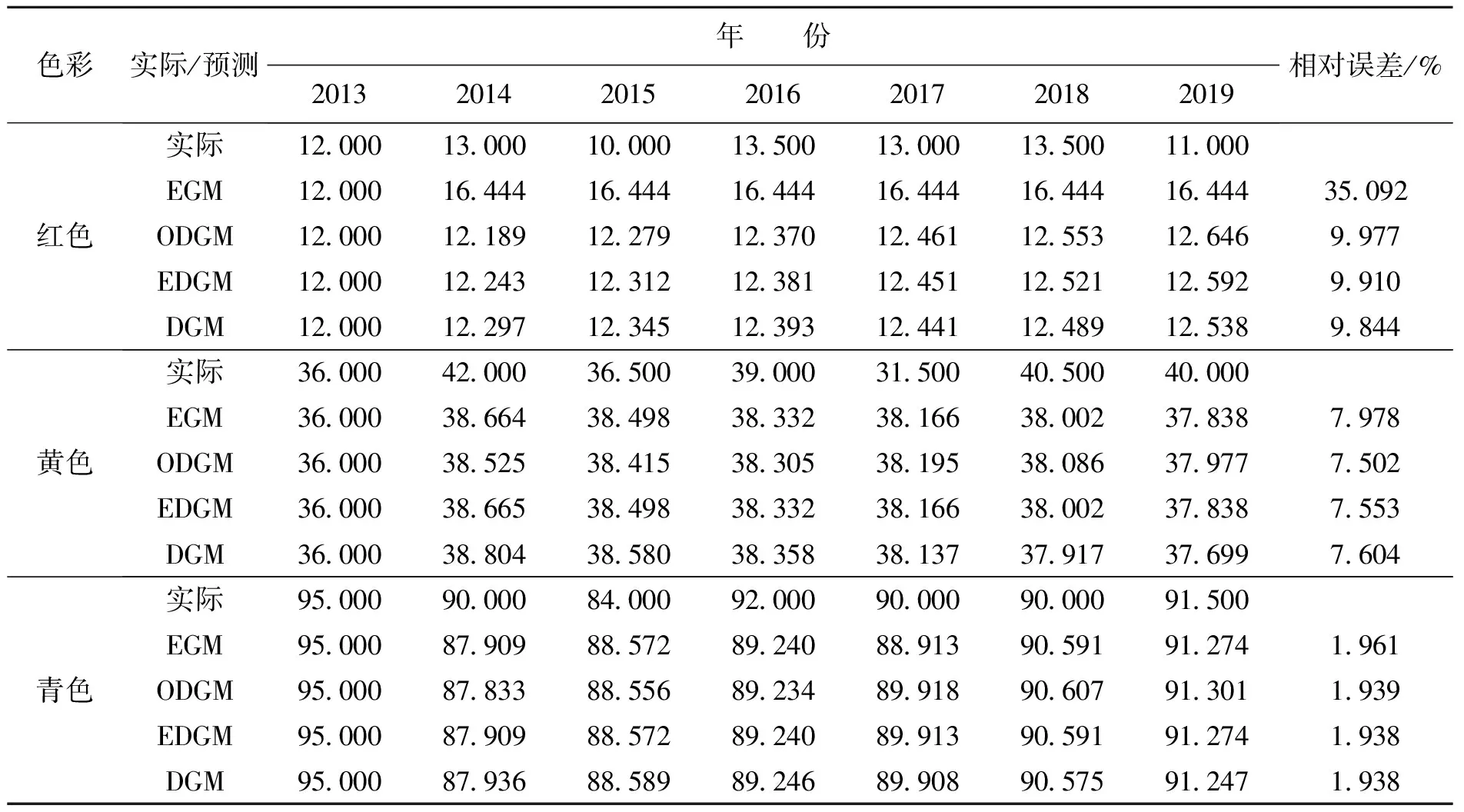
表 5 4种GM(1,1)模型拟合分析
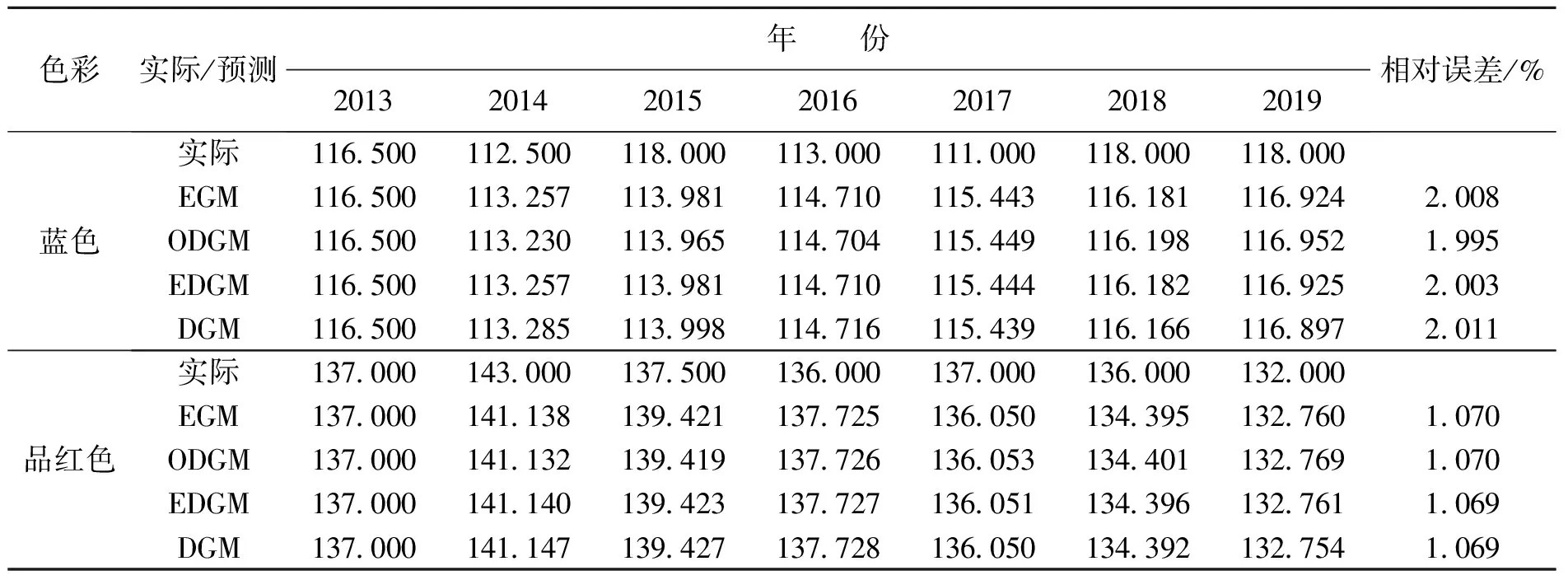
表 5(续) 4种GM(1,1)模型拟合分析
注:EGM、ODGM、EDGM、DGM分别表示GM(1,1)、ODGM(1,1)、EDGM(1,1)、DGM(1,1)模型预测值
从表5模型的拟合结果,计算得GM(1,1)、ODGM(1,1)、EDGM(1,1)、DGM(1,1)模型的平均相对误差依次为9.622%,4.497%,4.495%和4.493%,说明这4种模型预测精度均在90%以上,体现了灰色理论在小样本数据预测方面的优势。其中,DGM(1,1)模型的平均相对误差最小,模型精度等级为优秀;GM(1,1)模型的平均相对误差最大,精度等级为合格;ODGM(1,1)和EDGM(1,1)模型的平均相对误差介于两者中间,且与DGM(1,1)模型非常接近,模型精度等级同样达到优秀。可见:
(1) DGM(1,1)预测模型与另外3种模型相比,曲线拟合度理想,模型精度为优,可作为服装流行色的预测模型;
(2) 对于接近齐次指数序列的非指数序列和振荡序列,应优先选择DGM(1,1)模型、ODGM(1,1)模型或EDGM(1,1)模型;
(3) 常规GM(1,1)模型对黄色、青色、蓝色和品红色的预测性能与另外3种离散模型接近,说明GM(1,1)模型也可以对近似呈指数变化的时间序列建模。
为了更深入地研究4种GM(1,1)模型的预测稳定性,计算模型实际值与预测值之间的误差。4种模型的残差值曲线如图4所示。
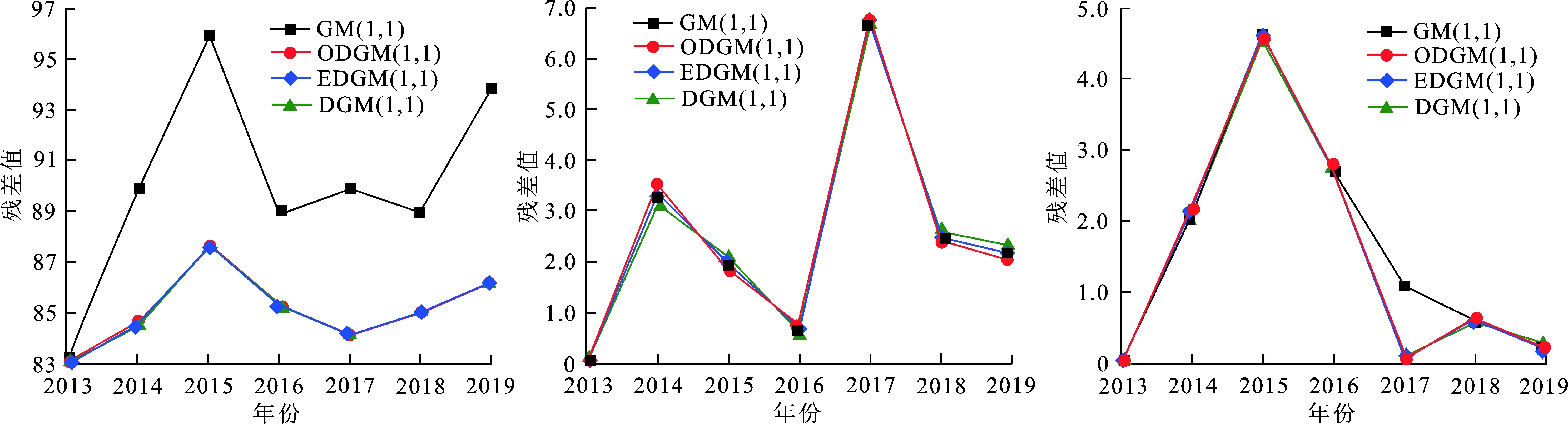
(a) 红色 (b) 黄色 (c) 青色
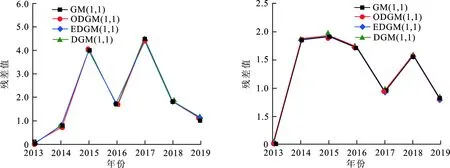
(d) 蓝色 (e) 品红色图 4 不同色彩的4种模型残差值曲线Fig.4 Residual curves of four models with different colors
观察图4可知,红色中GM(1,1)的残差值显著高于另外3种GM(1,1)模型,青色中GM(1,1)的残差值个别数据高于另外3种模型,黄色、蓝色、品红色中4种模型的残差值曲线几乎重合。说明常规 GM(1,1)对具有齐次指数数据序列的预测效果较好,但对波动性较大的数据拟合精度较差。此外,随着时间的推移,红色中4种模型的预测值较大幅度偏离实际值,可知红色更适合短期预测;黄色、青色、蓝色和品红色中4种模型的残差值随着时间的推移而缓慢降低,说明这4种色彩预测稳定性好,可进行中长期预测。整体而言,DGM(1,1)模型对各种色彩的预测性能最优,最适用于服装流行色的中长期预测。
综上所述,DGM(1,1)模型是4种模型中的最优预测模型,平均相对误差仅为4.493%,精度等级为优秀。但是,DGM(1,1)模型存在数学模型自身的局限性,只能描述数据的规律性,难以全面、准确反映各种非规律性的社会因素(如经济、战争等)对预测指标的影响,导致模型预测会出现较大的偏差。服装流行色的影响因素很多,各因素之间的关系不明确,随着时间的延长,预测精度将会降低。为了使预测结果更贴合实际情况,应进一步对现有DGM(1,1)模型进行预测修正,以减弱预测不稳定性所带来的影响。
4 结 论
(1) DGM(1,1)模型能有效弱化波动数据时间序列的影响,预测性能优于另外3种模型,有效提高了流行色预测精度,可为国内相关服装企业预测色彩趋势信息。
(2) 常规GM(1,1)对原始数据的光滑度要求较高,对波动数据时间序列的预测效果不理想;DGM(1,1)、ODGM(1,1)、EDGM(1,1)模型均能够精确拟合接近齐次指数序列的非指数序列和振荡序列,这3种模型的预测性能几乎相同。
(3) 4种灰色预测模型对红色的预测精度都不高,且残差值随着时间的推移会偏离实际值,红色适合短期预测;黄色、青色、蓝色和品红色的残差值随着时间的推移而趋于稳定,说明这4类色彩的数据规律性强,可进行中长期预测。

