数字流变特征的陶瓷凤纹函数建立及应用

熊 露，唐 敏，吴 琳，袁 枫，方 涛，郁永彬

(景德镇陶瓷大学 古陶瓷研究中心，江西 景德镇 333403)

0 引 言

凤纹作为中国传统陶瓷纹饰中富有强烈艺术美感和浓郁民族文化特征的代表之一，集中反映了前人的物质文化和精神文化的共识。这种贯穿整个中国历史的陶瓷装饰图案，在不同历史时期呈现出风格各异的的造型美，诠释着浓郁的本土化民族特色。据汉代许慎所著的《说文解字》对凤做出了解释，曰：“凤，神鸟也。天老曰：凤之象也，鸿前麟后，蛇颈鱼尾，鹤颗鸳思，龙文虎背，燕额鸡嚎，五色备举，出于东方君子之国，翱翔四海之外过昆仑，...”[1]，其大体特点是首如锦鸡，冠似如意，头如腾云，翅似仙鹤[2]，而不同时代有不同的生活条件和习惯，铸就了“大体则有，定体则无”的艺术特色。如果说远古时期，这种有意识的夸张且变形艺术作为部落图腾等装饰于黑陶、彩陶之上，显得淳朴而粗犷，那么唐宋时期或是清健、或是淡雅、或是华丽的风格演变，造就了凤纹逐步向修长秀丽方向发展，至于元明清时期，尤其是凤纹的规范化时期明代，线条清新明快，圆润传神[3]。但这些语言上的描述无法准确地给非专业科技工作者详实造型上的演变特征，同时数以万计的陶瓷凤纹遗存，对考古工作者的数据采集带来巨大的工作量，人为因素等导致的数据失真、数据遗失情况比较严重。而近年来国外学者不断引入计算机技术对考古数据进行分析研究，如数据库、人工智能的引入[4]等等，但作为初学者如何使用其他简单有效的数字化技术，将传统目测感官经验方法[5]进一步系统化、科学化和理论化，是纹饰研究乃至整个古陶瓷认知领域亟待解决的问题之一。

有鉴于此，本文尝试利用数据提取[6]、数据统计技术[7]等，以明、清时期陶瓷凤纹纹样为研究对象，探索不同时期凤纹纹样的细微差异性并进行分析和讨论，即通过数据提取技术和多元统计方法，得到不同时期凤纹纹样在数字上的流变，同时建立不同时期的判别函数，进而为科学准确区分不同时期陶瓷凤纹提供条件，也为古陶瓷认知提供新的科学依据。

1 实验部分

1.1 研究纹样概况

根据文献记载[8-10]，明清时期是陶瓷凤纹造型拥有共性形态和规范化的时代。凤纹在保持原有的大体特征外，这两时期已趋于定式，但无论是哪个时期都有其独特的内在形式和艺术表现手法。由于本文旨在揭示微观视角下的凤纹数字流变，故选取明清时期具有代表性凤纹纹饰作为研究样本，同时保证样本的真实可靠，选取为故宫博物院及上海博物馆馆藏等，其中编号M-01～M-11为明代陶瓷凤纹样品，Q-01～Q-02为清代样品。部分典型纹饰见图1。

1.2 研究方法

为使凤纹主体更加突出和醒目，对明清时期陶瓷进行纹饰采集过程中需要采用平视的拍摄手法，并将焦点集中在选定的纹饰图案上，以确保后期提取的数据信息准确和可靠[11]。获取原始图案后，通过图像精度增强、灰值转换、降噪和滤波等一系列的图像处理变换[12]，最终获得可供后期研究的凤纹边缘轮廓，具体处理流程如图2。

图1 部分典型纹饰Fig.1 Part of characteristic patterns

而在处理过程中，最为关键的步骤在于对凤纹轮廓的提取。在科学运算和自动控制与科学绘图领域，Matlab提供了几种常用的边缘检测算子[13-14]，以纹饰样品M-02为例，运用Sobel算子、Robert算子、Prewitt算子以及Laplacian算子对其进行纹饰边缘的提取识别，四种算子提取结果见图3。结果表明，针对于本文所选取的研究纹饰，Laplacian算子提取效果明显优于其他三种算子,在噪声和目标边缘间取得了较好的平衡，边缘连续性较好，同时纹饰的细节部分没有被消除，有效边缘得以保存完好，故本文采用Laplacian算子对纹饰进行处理，有效准确地提取出凤纹的边缘轮廓。

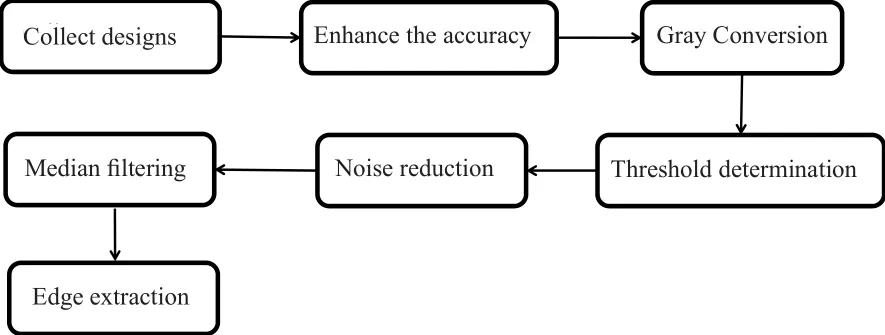
图2 处理流程图Fig.2 Processing fl ow chart

2 分析与讨论

2.1 凤纹头部数字流变

头部特征是研究动物学的重要部分[15]，头部指数可以反映头部各部分的比例关系，同时通过头部特征可以反映不同地域、不同时代等的指标类型。而陶瓷凤纹头部作为整体纹饰中微观的主要部分之一，其长宽指数 = (头最大宽/头最大长)即头最大宽与头最大长的比例，可以按照凤纹头长宽指数的大小反映长短的情况，其值越大表示凤头越偏短圆。凤纹样本头部数据指标见表1，其中k0为头部最大宽，k1为头部最大长，k2为长宽比例。为了对比明清时期凤纹头部的异同，利用多元统计软件对样本纹饰数据做了箱式图，如图4所示。从表1和图4中各指标参数可以看出，不同器型由于整体的比例大小导致凤纹头部长宽各异，但头部比例保持当代的风格，明代时期凤纹头部比例均值在0.4386左右，而到了清代比例有所上升，均值达到了0.7142左右。两个朝代头部比例均值差异性比较大，凤纹头部由明朝的狭长逐步向清朝的短圆发展。而从箱式图中几个误差点的显示可以看出，M-07样本纹饰与明时期均值相差较大，应属于明早期的纹饰样本，M-08样本纹饰均值比较靠近清早期指标，应属于明晚期接近清早期时代纹饰样本，Q-01指标为0.5105接近于明朝指标，可能属于清早期纹饰样本。

图3 四种算子提取Fig.3 Extraction results by four operators

图4 头部比例箱式图Fig.4 Box fi gure for head proportions

对于明清两朝凤纹头部比例的流变，导致其演变的主要原因可能有两个因素，一是时代精神，二是风俗情况。中国历史上明代是一个封建专制比较严重、同时高度发展的中央集权制度也是那个时代的明显特征，作为贫贱出生的开国皇帝恢复汉族正统之后，对前朝民族实施高压政策，制定严格的等级制度，这就直接导致专供皇家使用的陶瓷器装饰艺术上突出这一风俗的形式出现，狭长的头部极富东方情调，又不失神气逼人。而清代爱新觉罗氏属于满族人群，采用联姻等怀柔政策联合蒙古族抵御外敌，一直持续到清朝结束，所以满族和蒙古族在时代精神和风俗情况上具有一定的共通性，也就是清代的艺术形式和元代的有共同点，从凤纹头部比例指数来看，清代头部比例均值比较大，导致给人以短圆的视觉感受，比较接近元代时期的温柔雅致，又不失善战尚武的时代精神。因而，不同时代不同风俗的因素可以导致凤纹纹饰头部比例的数字变化，同时数字流变也同样可以反映各个时期的时代精神和风俗情况。

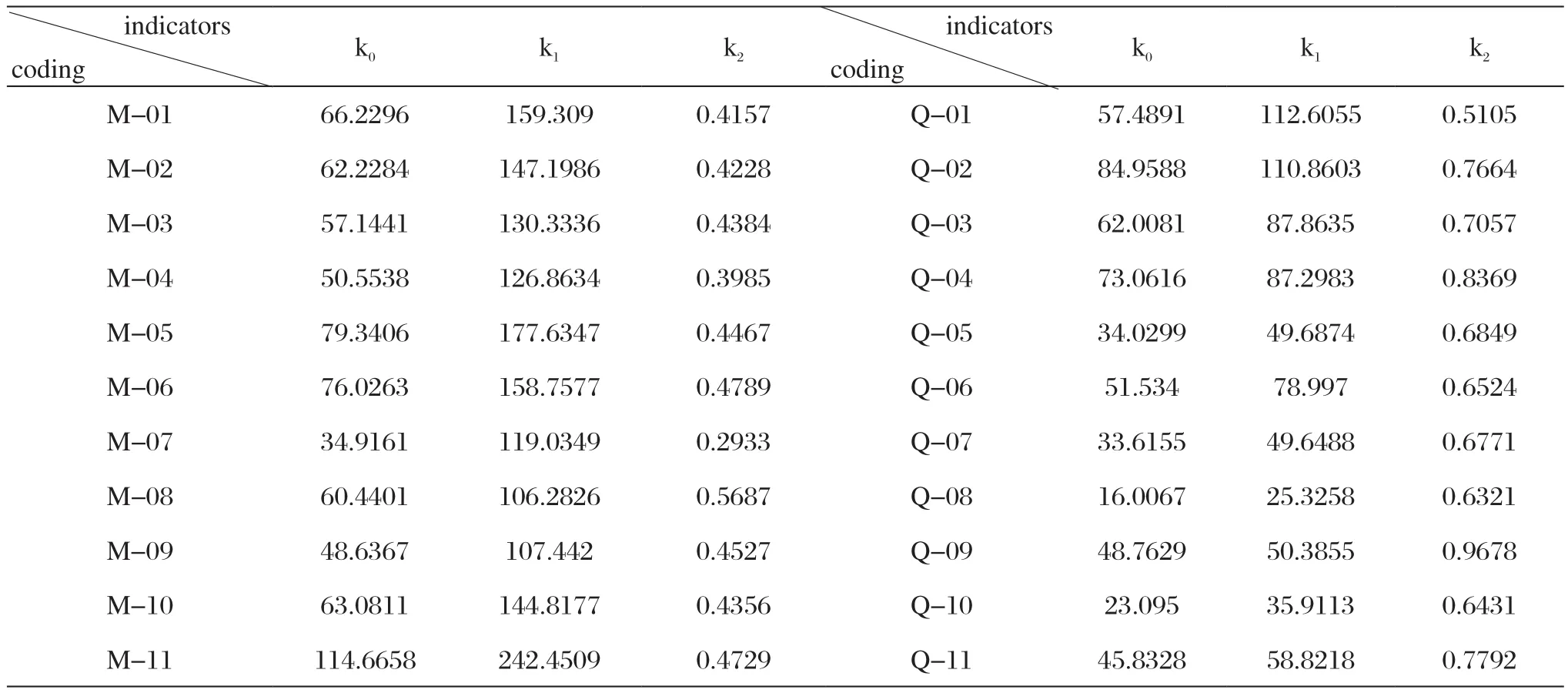
表1 数据指标Tab.1 Data and indicators

2.2 判别函数建立

以往考古绘图中，量取曲线的方式一直还停留在手工绘制的阶段，需要对纹饰进行手工拉取基线等等[16]，绘制速度慢和图形精度低等因素直接影响后续工作和研究的深入。而本文恰恰有效解决了这一问题，利用MATLAB软件对纹饰进行提取和数据存储，使纹饰图案保存简单高效和快捷。前期仅仅获取凤纹头部比例数据，并不能很好的体现数字流变特征分析的优势，本文同时利用判别分析对数据流变特征进行归纳。纹饰图案是由一条条未知曲线构成，而曲线长度是最为关键的因素之一，而计算颈脖长度就需要对颈脖的轮廓线进行拟合，本文利用Matlab软件[17]进行轮廓线的三阶函数拟合，得到的曲线拟合度已与样本原始轮廓较接近，表2中S为明清时期凤纹颈脖的拟合曲线表达式。提取曲线表达式后，利用数学上定义曲线长度的公式使用SPSS软件对凤纹的颈脖长以及颈脖最大宽进行数据分析，表2中L为凤纹颈脖长度，k3为凤纹颈脖最大宽度，k4为颈脖长与最大宽比例。

由表1、表2数据可以看出，不同时期的凤纹数据确实存在不同的数据流变，以费希尔方法为基础，对凤纹的数据特征进行判别函数的建立。本文选取了明清时期的凤纹为主要研究对象，故判别给出两个非典型性判别函数，表3为明清时期凤纹数据流变判别函数。

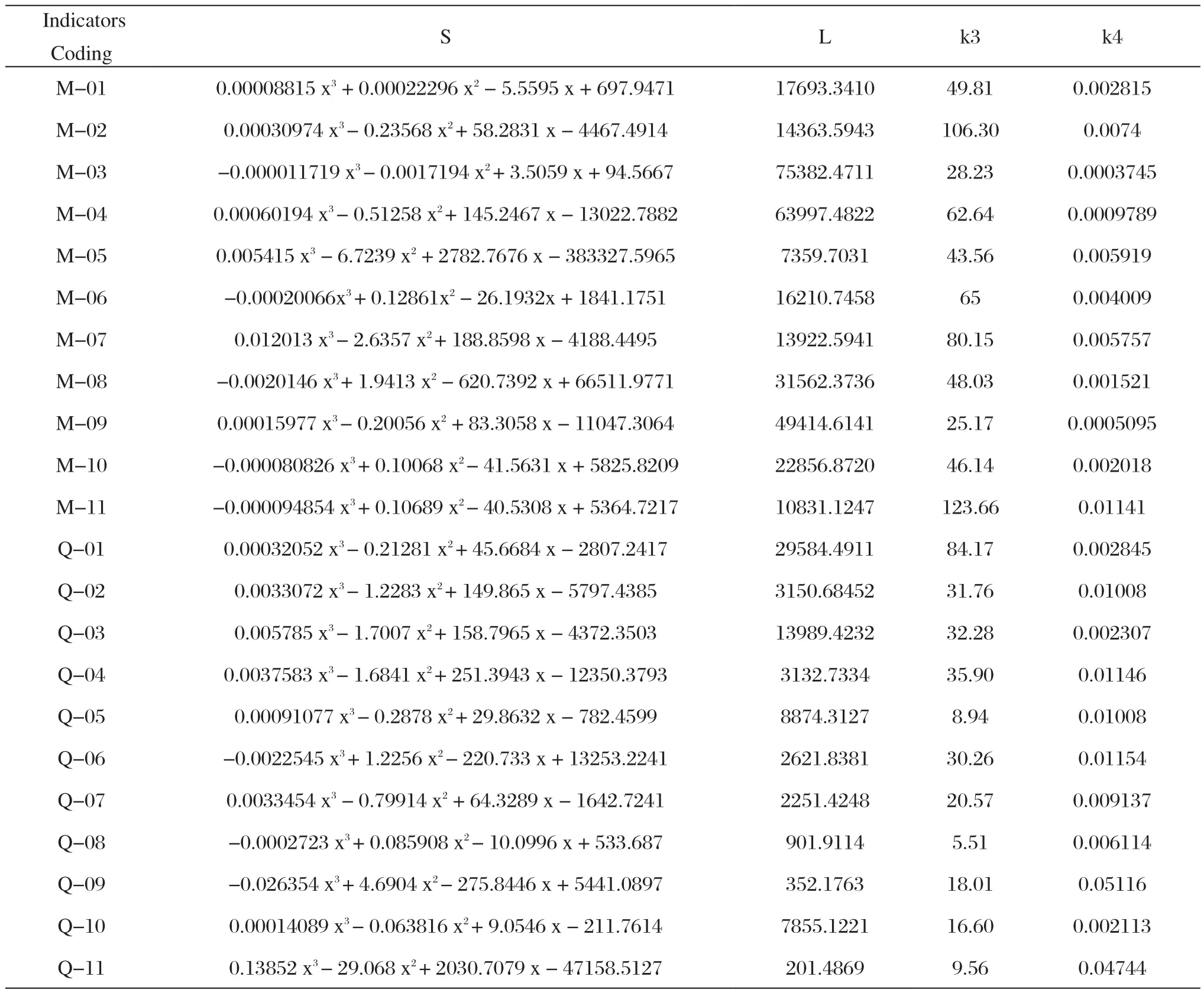
表2 颈脖数据Tab.2 Neck data

表3 判别函数Tab.3 Fisher's linear discriminant functions

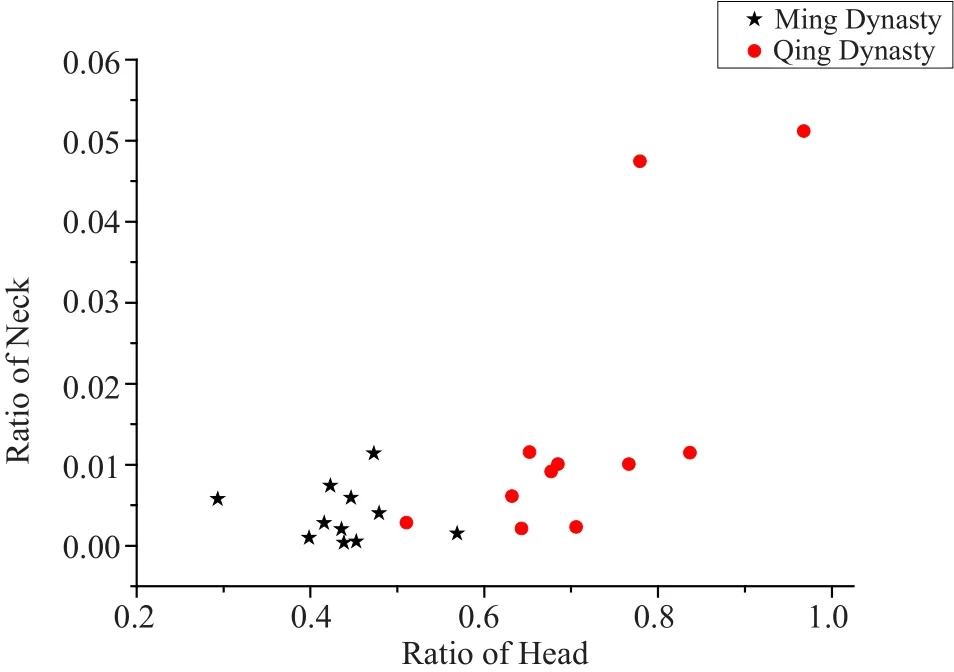
为检验两组判别函数的准确性，随机选取样本中的一个进行回代检验，如选取M-10样本，将其各特征变量代入费希尔判别函数，F(1) =15.2233，F(2) = 10.3634，其中F(1)函数值最大，可判断M-10样本可归为第一组，即为明代凤纹纹饰，与事实相符。同时，将具有典型时代特征的梅瓶结构特征数据用ORIGIN判别分析绘制成纹饰分期区域散点图，如图5所示，利用样品的数据流变特征较明显的将两个朝代的凤纹区分开，图5中数据位于左下部分的为明代凤纹样品，右边大部分区域数据为清代样品，凤纹样品分期情况还是比较明显的。从此类数据流变同样可以看出，明代凤纹相较清代凤纹略显清秀，印证了明清的时代特点以及由此产生的艺术形式。而利用此类方法，能有效的对不同时期凤纹纹饰进行甄别。

3 结 论

以我国传统纹饰中具有代表性的凤纹为例，利用数据提取和数据分析技术等，揭示凤纹微观部分的数据流变。结果表明：

(1)利用数据提取、数据分析等技术研究陶瓷纹饰变化，不仅提高了工作效率而且提高了数据提取的准确性和可靠性。不同时代的社会审美和民族风俗能够通过数据上的流变反映出来，同时数据上的流变也可以体现社会的变革和时代的发展；

(2)利用纹饰结构数据的流变特征建立判别函数，可以有效地对不同时期纹饰进行甄别，特别是根据纹饰数据的流变特征进行分析，能较准确、可靠的对古陶瓷文物进行认知，有助于把古陶瓷类文物传统鉴定模式中的感官信息和经验进行更为有效的定量化和系统化，为古陶瓷类文物数据的积累和传承提供条件；

当然，由于陶瓷纹饰大多是在曲面上进行数据提取，会存在一定的误差，需要充分利用现代摄像技术及数据处理技术对纹饰进行数据还原拟合，同时还可使用3D扫描成像法提取纹饰曲线等等。总之，数字化方法运用于陶瓷纹饰的认知研究具有重要的意义和广阔的应用前景。