立柱分布对陶瓷干法造粒混料过程的数值模拟
郑 琦,邓佩瑶,刘子硕
(景德镇陶瓷大学 机械电子工程学院,江西 景德镇 333403)
0 引 言
球磨—喷雾湿法造粒[1]是目前普遍采用的陶瓷造粒制粉工艺方法,其制得的颗粒能很好满足各类陶瓷墙地砖生产需求,但该技术带来的高能耗、高污染、高投入等问题严重阻碍了其发展[2-3]。而干法造粒技术可以节约60%能源消耗,80%的耗水量及74%的大气排放物[4],在国家对陶瓷工业污染物排放进行严格限定的背景下,干法造粒技术是未来发展的主要方向。
干法造粒技术的发展目前仍处于起步阶段,要使其在陶瓷生产企业中得到推广,主要需要解决陶瓷干法造粒技术中存在的真颗粒充分分散性问题、假颗粒成形压缩比问题以及粉体的混色、发色问题[5-7]。其中立柱分布在搅拌过程中对颗粒是否充分分散有一定的影响,然而在实验过程中无法实时测量搅拌流场的状态,故采用计算流体动力学方法对其进行数值模拟[8]。长期以来,许多专家学者都对搅拌流场的特性进行了广泛研究。陈禹等[9]采用CFD方法对刚性圆柱进行数值模拟,表明不同雷诺数下圆柱绕流在性质上存在较大的差异。刘为民等[10]研究了阵列四柱绕流的数值模拟,引入雷诺平均法求解NS方程,结合SST、k-ω湍流模型对海洋结构物涡流场进行了研究。郭传山等[11]研究了两种典型截面立柱绕流特性数值模拟,采用Fluent对这2种截面形式的立柱进行不同折合速度和不同来流角度下的绕流数值模拟。张海鹏等[12]对不规则柱体绕流进行了数值模拟,发现不规则柱体会对绕流产生一定的影响。虽然许多学者对搅拌流场的特性进行了深入的研究,但对造粒室内立柱分布不同时的搅拌流场特性却鲜有报道。
结合前人的经验,在已有的研究基础上,采用CFD(Computational fluid dynamics)方法,通过建立欧拉-欧拉双流体模型[13]对基于立柱分布的陶瓷干法造粒混料过程进行数值模拟,分析了干法造粒机内不同立柱分布对陶瓷原料颗粒的混料效果,其研究成果对陶瓷干法造粒技术的推广具有一定指导意义。
1 造粒室的结构与尺寸
1.1 造粒室整体结构
图1为造粒室结构示意图,结构主要分为筒体、筒盖、搅拌主轴、铰刀、叶片、粉体颗粒。造粒室内径为235 mm、高为300 mm,初状态加入陶瓷原料粉体约占造粒室体积的1/4(高度约为75 mm)。
1.2 造粒室结构

图1 造粒室整体结构示意图Fig.1 Overall structure diagram of prilling chamber

图2 立柱结构示意图Fig.2 Schematic diagram of column structure
图2为立柱形状结构示意图,直径d1= 10mm、长度L = 300mm,底部挡柱中心距底部圆心90 mm,粉碎铰刀等距均匀分布为18个锯齿型结构,立柱分布为9个圆柱型结构。
1.3 造粒室内介质及流动状态
造粒室内存在的介质主要为粉体颗粒和空气,其属于非牛顿流体。流动雷诺数Re计算公式如下:

式中,Re为流动雷诺数;p为介质密度,经实际分析为2047 kg/m3;N为铰刀转速;μ为动力粘度,经实际分析为0.32 Pa·s;D为铰刀直径,即128 mm。笔者根据实际铰刀转速以计算流动雷诺数,当N为2400 r/min时,计算雷诺数为4200.2,此雷诺数Re > 4000,流体呈湍流状态。
2 数理模型
2.1 数学模型
该造粒室内粉体颗粒粒径大约为0.013 mm,故可将坯料颗粒作为拟流体相,流体在流动过程中符合相关物理守恒定律。在混料过程中粉体相与空气相同时存在,粉体相与空气相相互共存和共融[14]。混料过程使用欧拉-欧拉模型来求解分析,并且必须满足动量守恒方程和连续守恒方程[15]。具体数学模型公式如下:
⑴连续性的守恒方程
粉体相的连续性守恒方程:
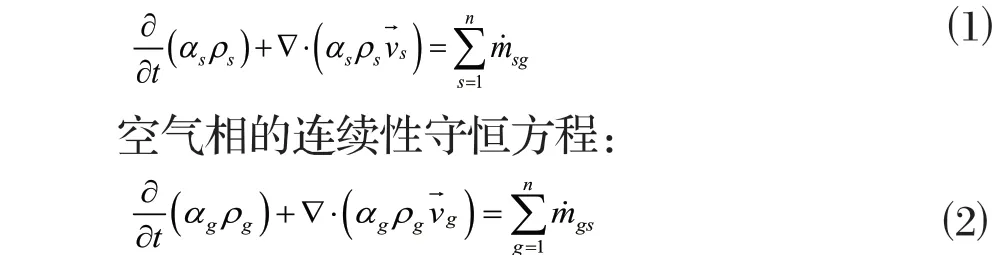
式中,αs为粉体相的体积分数比,αg为空气相的体积→分数比;ρs为粉体相的→密度,ρg为空气相的密度;vs为粉体相速度矢量,vg为空气相速度矢量;ṁsg为粉体相质量传递、ṁgs为空气相质量传递(ṁgs = -ṁsg)。
⑵动量守恒方程
粉体相动量守恒方程:
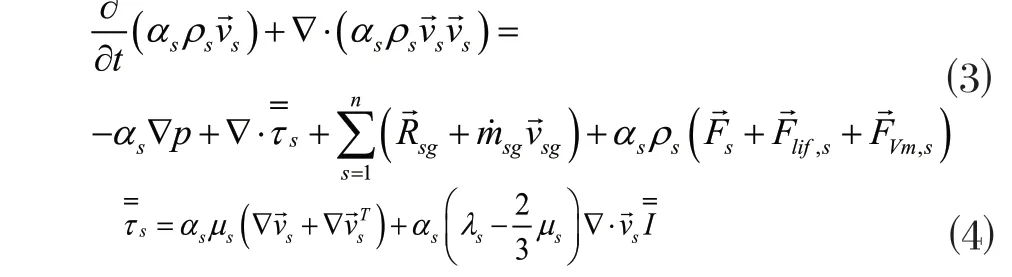
空气相动量守恒方程:
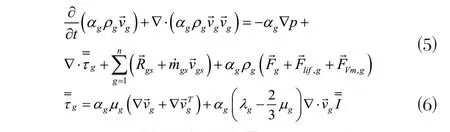
式中,μs为粉体相的分子粘度;λs为粉体相的体积粘度,μg为空气相的分子粘度; λg为空气相的体积粘度为粉体相的体积力空气相的体积力;为粉体相的上升力为空气相的上升力为粉体相的模拟质量力为空气相的模拟质量力;分别为粉体相与空气相之间的相互作用力,且两相之间是相对封闭的;p为粉体相与空气相共有的压力为粉体相的应变张量为空气相的应变张量为粉体相与空气相的单位张量。
2.2 物理模型
2.2.1 边界条件
其中搅拌主轴、立柱、铰刀叶片和造粒室壁面都设定为墙(wall),由于搅拌主轴的旋转速度很大,因此陶瓷原料粉体在搅拌叶片、铰刀临近区域受搅拌的作用影响大,故将该临近区域设置成动计算区域,动计算区域在Fluent中设置为滑移网格(Moving mesh),其它区域设置成静区域(Static zone),静计算区域设置为多重参考坐标系法(Multiple reference frame),动计算区域与静计算区域设定为交界面(Interface)相连,用于动、静计算区域流体数据交换。整个造粒室模拟区域处于封闭状态,即其它面都设定成墙。
2.2.2 建立模型与网格划分
使用SolidWorks软件分别建立三种立柱分布的造粒室实体模型,然后再进行布尔减运算再导入前处理软件ICEM-CFD中生成计算区域结构模型。由于铰刀、叶片临近区域几何造型比较复杂,流场强度较大,故选用四面体网格进行划分,网格大小设置为6,造粒室其他区域选用以六面体为主四面体为辅的网格进行划分,网格大小设置为5.5。将整个计算区域划分为两个区域:铰刀、叶片临近区域为动计算区域,剩余区域为静计算区域。如图3所示,立柱呈正方形分布时造粒室网格单元数为183306个;呈圆形分布时造粒室网格单元数为183299个;呈菱形分布时造粒室网格单元数为183307个。
2.2.3 数值求解
通过计算流体力学方法对造粒室内流场动态进行数值模拟。自定义边界条件并且对欧拉-欧拉双流体模型进行数学模型修正以更好的符合本数理模型。采用压力隐式求解算法求解非稳态时的流场,通过修正后的欧拉-欧拉双流体模型模拟流场分布情况,湍流模型选用k-ε模型中的RNG离散模型,离散相应用一阶迎风,压力-速度耦合相采用Phase Coupled SIMPLE算法,所有变量收敛残差值均小于1×10-3。

图3 网格划分示意图Fig.3 Sketch map of mesh generation
3 数值模拟结果与讨论
3.1 颗粒体积分布轴向云图分析
颗粒体积分布轴向云图如图4所示,由图4可知:当造粒时间为5 min,颗粒主要堆积均在造粒室底部和上部桶壁。当立柱形状为菱形时,颗粒体积分数大于0.20的颗粒体积约占总体积的16%,堆积现象较为明显,体积分数在0.18-0.20之间的颗粒体积约占总体积34%,体积分数在0.16-0.18之间的颗粒体积约占总体积的14%;当立柱形状为圆形时,颗粒体积分数大于0.20的颗粒体积约占总体积的9%,堆积程度相比菱形有一定改善,体积分数在0.18-0.20之间的颗粒体积约占总体积28%,体积分数在0.16-0.18之间的颗粒体积约占总体积的20%;当立柱形状为正方形时,颗粒体积分数大于0.20的颗粒体积约占总体积的19%,堆积程度最为严重,体积分数在0.18-0.20之间的颗粒体积约占总体积42%,体积分数在0.16-0.18之间的颗粒体积约占总体积的6%。总体而言,当立柱分布为圆形时,堆积最少,造粒室中部颗粒体积分布更为均匀,造粒效果相对较好。
3.2 颗粒体积分布径向云图分析
颗粒体积分布径向云图如图5所示,取距离底面高度20 mm处XY面颗粒的分布情况,由图5可知:当立柱形状为菱形时,颗粒体积分布在0.225以上的面积约占平面70%,颗粒在此平面上堆积现象严重;当立柱形状为圆形时,体积分数在0.225以上的面积约占平面30%,仅在铰刀附近区域有一定的堆积;当立柱形状为正方形时,体积分布在0.225以上的面积约占平面55%,仍然存在大量堆积,但较立柱形状为菱形时有一定改善。综上所述:立柱形状为圆形时最好,发生堆积的面积相对较少。

图4 颗粒体积分布轴向云图Fig.4 Axial nephogram of grain volume distribution
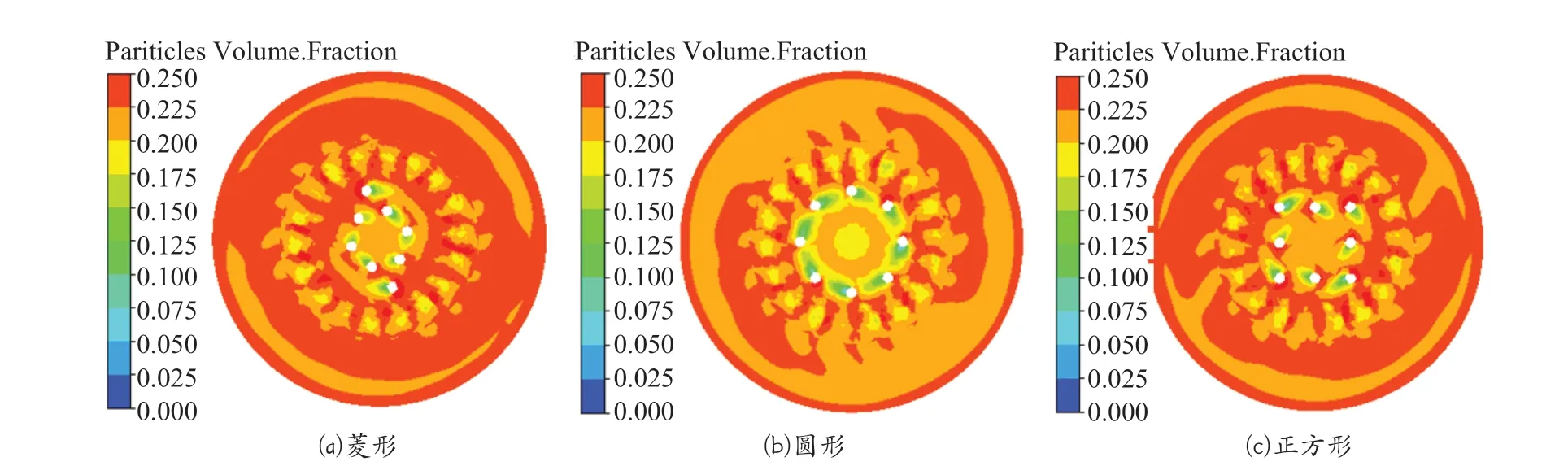
图5 颗粒体积分布径向云图Fig.5 Radial nephogram of particle volume distribution

图6 颗粒速度云图Fig.6 Velocity nephogram of particles
3.3 颗粒速度云图分析
颗粒速度云图如图6所示,取距离底面高度138 mm处XY面颗粒运动速度的分布情况。由图6可知:当铰刀立柱形状分别为菱形、圆形、正方形时,颗粒速度大小均分层分布,桶壁颗粒速度最小,桶壁与铰刀中间区域速度稍大,铰刀附近速度最大,然后铰刀到造粒室中心速度逐渐变小,造粒室中心速度最小。当立柱形状为菱形时,颗粒运动速度在0.10-0.15之间的面积约占32%,主要分布在桶壁和菱形内部,此区域速度较慢,颗粒混合效果不佳;当立柱形状为圆形时,运动速度在0.10-0.15之间的面积约占18%,主要分布在桶壁和圆形周边区域,颗粒混合效果有明显改善;当立柱形状为正方形时,运动速度在0.10-0.15之间的面积约占38%,同样主要分布在桶壁和正方形区域内,此速度较小的区域面积相对于菱形更大,更容易产生堆积,颗粒混合效果更差。综上所述:立柱形状为圆形时,在桶壁和造粒室中心区域堆积相对较少,混合效果最好。

表1 坯料颗粒粒径分布Tab.1 Particle size distribution of blank particles
4 实验分析
4.1 坯料颗粒制备
溶剂性原料、可塑性原料和瘠性原料是实验所需的主要原料。熔剂型原料有钾长石、钠长石、钙长石、大理石、石灰石;可塑性原料有黏土、高岭土、膨润土;瘠性原料有石英、石英砂;加入总质量为2.5 kg的实验原料,其中石英0.250 kg、石英砂0.175 kg、钾长石0.350 kg、钠长石0.250 kg、钙长石0.175 kg、大理石0.300 kg、石灰石0.200 kg、黏土0.400 kg、高岭土0.250 kg、膨润土0.150 kg。所需造粒添加剂有海藻酸钠、邻苯二甲酸二丁酯、聚乙烯醇、聚丙烯酰胺、聚甲基丙烯酸甲酯和水,且造粒添加剂含量不超过总质量的5%。造粒添加剂的配比为:6%的海藻酸钠、3%的邻苯二甲酸二丁酯、5%的聚乙烯醇、6%的聚丙烯酰胺、5%的聚甲基丙烯酸甲酯和75%的水。
制备陶瓷坯料颗粒的工艺如下:首先将瘠性原料、熔剂性原料和可塑性原料按上文的配比加入干法造粒室内,待充分混合均匀,再将配好的造粒添加剂采用超声雾化喷嘴均匀喷洒至造粒室内,陶瓷粉体与雾化液充分混合实现造粒效果,造粒结束将坯料颗粒卸出造粒室,并待检测分析。
4.2 检测分析与实验结果
对于三种不同形状的造粒室立柱分布,分别制备陶瓷干法造粒坯料颗粒,筛分坯料颗粒以获得相关粒度分布如表1所示。当立柱分布为菱形时,粒径为20-80目的有效坯料颗粒占70%,颗粒集中分布在20-60目,约占整体的52%;当立柱分布为圆形时,有效坯料颗粒占82%,颗粒集中分布在30-60目,约占整体的51%;当立柱分布为正方形时,有效坯料颗粒占64%,颗粒集中分布在20-70目,约占整体的64%。由对比分析可得:当立柱分布为圆形时,有效坯料颗粒所占比例最大为82%,此时坯料颗粒级配最优。
5 结 论
⑴研究表明,造粒立柱分布为圆形时,混料过程粉体堆积现象不明显,速度相对较均匀,分散性及流动性较好,有效颗粒占比最大,造粒效果最佳。并且结合实验结果可知造粒立柱分布为圆形时,颗粒的流动性以及级配最佳。
⑵基于CFD方法建立了不同造粒立柱分布混料过程的数理模型,并通过实验验证了数值模拟结果的正确性,说明了数理模型的可靠性,为陶瓷干法造粒过程可视化研究提供了相关理论依据。

