蒸渗仪测定滴灌枣树不同时间尺度下腾发强度特征*

郭丹丹, 马英杰, 马 亮



蒸渗仪测定滴灌枣树不同时间尺度下腾发强度特征*

郭丹丹, 马英杰, 马 亮**

(新疆农业大学水利与土木工程学院 乌鲁木齐 830052)

为精确测定、准确模拟阿克苏地区滴灌枣树腾发过程, 基于大型称重式蒸渗仪测定枣树全生育期逐时及逐日腾发强度(ET), 利用水量平衡方程、PM公式及经典统计原理, 分析不同时间尺度下叶面积指数(LAI)、气象因素[温度()、风速()、净辐射(n)]、表层土壤含水率()与枣树腾发强度的相关关系并建立预测模型。结果表明: 枣树日内腾发强度呈单峰型变化趋势, 夜间变化幅度较小且腾发贡献率低。枣树全生育期逐日腾发强度变化呈先增大后减小的趋势, 花期的腾发强度最大, 为4.42 mm∙d-1; 全生育期腾发总量为640.83 mm, 其中花期和果实生长发育期耗水量占比较大, 分别为38.61%和32.72%。在小时和日时间尺度上, 影响腾发强度的主要因素不完全相同, 且影响程度有所差异。综合考虑各影响因素, 以萌芽期、花期、果实发育期为基础, 分别建立以小时、日尺度下估算腾发强度的经验模型ET1(h)=0.153+0.004+0.012+0.176n+0.002+0.067LAI、ET2(d)=-3.325+0.081+0.163n+0.069+2.089LAI, 拟合度2均在0.7以上, 以果实发育期与成熟期数据对模型进行检验, 纳什效率系数分别达0.63、0.80。经偏相关检验, 冠层净辐射(n)对两种尺度的腾发强度均影响最显著, 因此以枣树全生育期数据量为基础, 仅建立冠层净辐射(n)与腾发强度的回归模型ET1(h)=-0.063 3n2+0.361 2n−0.003 7、ET2(d)=-0.018 3n2+0.684 7n–1.642 1,2分别为0.704 7与0.743 6, 可满足缺少数据支撑情况下的腾发过程估算。这些模型明确了阿克苏地区滴灌枣树腾发机制及影响程度, 可为水分管理精准化提供计算基础。

腾发强度; 气象因子; 时间尺度; 枣树; 滴灌

田间腾发强度的精确测定、模拟可为准确估算土壤水分、预测农田干旱的发生和作物水分胁迫状况提供重要信息[1], 是制定农作物灌溉制度的基础, 也是促进农业节水的关键[2-4]。红枣(Mill.)抗寒抗旱, 耐盐碱, 适应性强, 可减小干旱区降雨少、蒸发量大、盐碱地严重等对农业生产的影响。新疆光热丰富, 昼夜温差大, 是我国优质干枣生产基地, 目前新疆红枣种植面积47.37万hm2, 占水果总面积的46.66%[5-6]。研究枣树的腾发量已有不少结论, 王则玉等[7]采用TRIME水分监测仪测定每次灌水前后土壤含水量, 得出不同灌水处理下9 a枣树腾发量为579.6~668.2 mm; 曹俊[8]采用DIVERN2000每5 d观测一次土壤含水量, 得出不同处理下8 a生成龄枣树腾发量为410.7~472.0 mm。以上枣树腾发量测定时间间隔较长, 且随着灌水结束便终止测定枣树腾发量, 测定结果不完整。大型称重式蒸渗仪可控制土壤边界条件, 直接测定冠层尺度的腾发强度, 测定时间间隔短, 精度高, 目前被认为是测量作物腾发强度最准确的仪器。国内外利用蒸渗仪测定作物腾发强度已经非常普遍, 研究对象多为小麦(L.)、玉米(L.)等一年生作物[9-11], 少见对多年生果树的研究, 滴灌枣树水分精准化管理缺少有力的理论知识。

模拟腾发强度以预测作物需水量是灌溉预报的关键[12]。腾发过程主要受土壤因素、大气因素、作物自身因素影响, 众多因素间的关系错综复杂[13]。汪秀敏等[14]发现环境因子对冬小麦腾发强度影响大小为净辐射>空气相对湿度>土壤温度>空气温度> 40 cm土壤含水量>风速; 杨光超等[15]研究表明, 日照、风速对腾发强度的影响超过了温度。目前各学者建立预测腾发强度的模型时, 仅关注气象条件对腾发强度的影响, 考虑影响腾发强度的因素不够全面, 且得出的结论有所差异。本文使用大型称重式蒸渗仪精确测定枣树逐时及逐日腾发强度变化趋势, 测定截止时间为枣成熟期(采摘结束), 得出一个完整的枣树全生育期腾发量。同时以蒸渗仪实测枣树腾发强度为基础, 分析不同时间尺度下(小时、日)腾发强度与各影响因子间的关系, 建立回归模型, 为满足不同灌溉要求下预估作物需水量提供参考。

1 材料与方法

1.1 试验区概况

试验区地处新疆阿克苏地区红旗坡农场新疆农业大学林果实验基地(80°14¢E, 41°16¢N), 属于典型的大陆性温带干旱沙漠气候, 海拔1 133 m。实验站内气象站测得2014—2017年5—10月间平均降雨量为80.25 mm, 平均地表太阳辐射量为197.96 MJ∙m-2∙d-1, 平均温度达19.41 ℃。土壤为砂壤土, 0~100 cm土层平均土壤容重为1.46 g∙cm-3, 平均田间持水量25.4%。试验时间为2017年枣树全生育期。

试验区设有大型称重式蒸渗仪, 箱体内种植两棵2013年嫁接枣树, 供试枣树品种为‘灰枣’。根据作物参考腾发量(ET0)与作物系数(c)[16]计算各时段腾发量(ET)确定灌溉量, 采用定周期制度(每隔7 d, 可调节), 灌溉方式为滴灌, 一行双管布设在枣树两侧30 cm处, 滴头流量为3.2 L∙h-1。箱体周围架设直径0.5 m、高度1 m的马氏瓶, 高度为3 m, 连接迷宫式滴灌带灌溉。试验期间施肥与其他管理措施与当地农田相同。

1.2 试验设计

1.2.1 观测内容及方法

枣树全生育期的腾发强度由大型称重式蒸渗仪测定(称重系统可直接测定土体水重与渗漏量), 箱体面积为3 m×2.2 m, 深3 m, 箱体内装有与试验地土壤类型一致的原状土, 测量精度为±0.1 mm。土壤水分数据由蒸渗仪自带的5TE采集器获得, 测量值为体积含水率, 测定土壤深度为10 cm、20 cm、30 cm、50 cm、70 cm、90 cm、130 cm、170 cm, 本文选取10 cm、20 cm的平均土壤含水率为表层土壤含水量。试验站内设有HOBO小型自动气象站, 安装高度为2 m, 可测定温度、相对湿度、地表太阳辐射、2 m处风速、降雨量等气象数据。HOBO小型自动气象站、大型称重式蒸渗仪及自带的5TE土壤水分采集器的测定时间间隔均为0.5 h。

叶面积指数测定需在太阳升起之前进行, 用带有鱼眼广角镜头的单反数码相机采集每株枣树东、南、西、北4个方向半球影像图片, 并采用HemiView数字植物冠层分析系统分析, 取平均值为枣树叶面积指数, 测定时间间隔为10 d, 内差法获得其余天数的叶面积指数。

1.2.2 数据处理

称重式蒸渗仪测定植株的腾发量, 其基本的计算原理是水量平衡方程[17-19], 即:

ET = ∆++–– ∆(1)

式中: ET为枣树腾发量; ∆为土壤含水量的变化量, 即蒸渗仪土柱质量的变化, 本研究所用蒸渗仪6.6 kg质量变化对应为1 mm的土壤水分变化;为土壤保存的有效降雨量, 包括降雨和露水;为灌溉水量, 蒸渗仪与大田的灌水量、灌水日期均一致;为地表径流, 由于本试验区域的降雨不足以造成径流, 故可以忽略; ∆为时段内的渗漏量, 通过蒸渗仪配套安装的渗漏桶测量。以上变量单位为mm或m3∙hm-2。

采用联合国粮农组织(FAO)推荐的Penman- Monteith(简称PM)[17]方法计算日尺度下参考作物蒸发蒸腾量(ET0)。美国工程师协会-环境与水资源机构(ASCE-EWRI)提出的标准Penman-Monteith(简称ASCE-PM)模型计算小时尺度下ET0与冠层净辐射量(n)[20-21], 计算公式为:

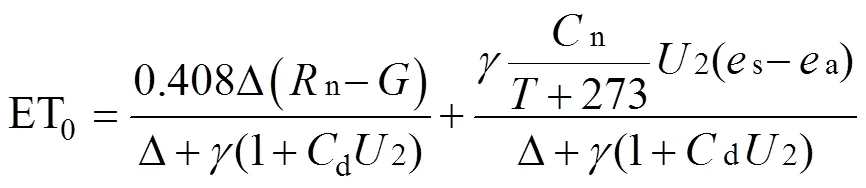
式中: ET0为参考作物腾发量(mm∙d-1或mm∙h-1), 其余各参数表示及计算过程可参考[17,20]。n、d是随着白天(夜晚)作物冠层表面空气动力阻力的变化系数, 计算时间步长不同时n和d取不同的系数。n的单位为K∙mm∙s3∙mg-1∙d-1或K∙mm∙s3∙mg-1∙h-1,d的单位是s∙m-1。本文采用FAO-56计算日尺度下ET0, 其中n取值为900 K∙mm∙s3∙mg-1∙d-1,d取值为0.34 s∙m-1; 采用ASCE-PM计算小时尺度下ET0,n取值为37 K∙mm∙s3∙mg-1∙h-1,d白天取值为0.24 s∙m-1, 夜间取值为0.96 s∙m-1。

通过Microsoft Excel 2013进行数据计算、归一化处理及绘图, 用DPS16.05软件进行多元线性回归分析。

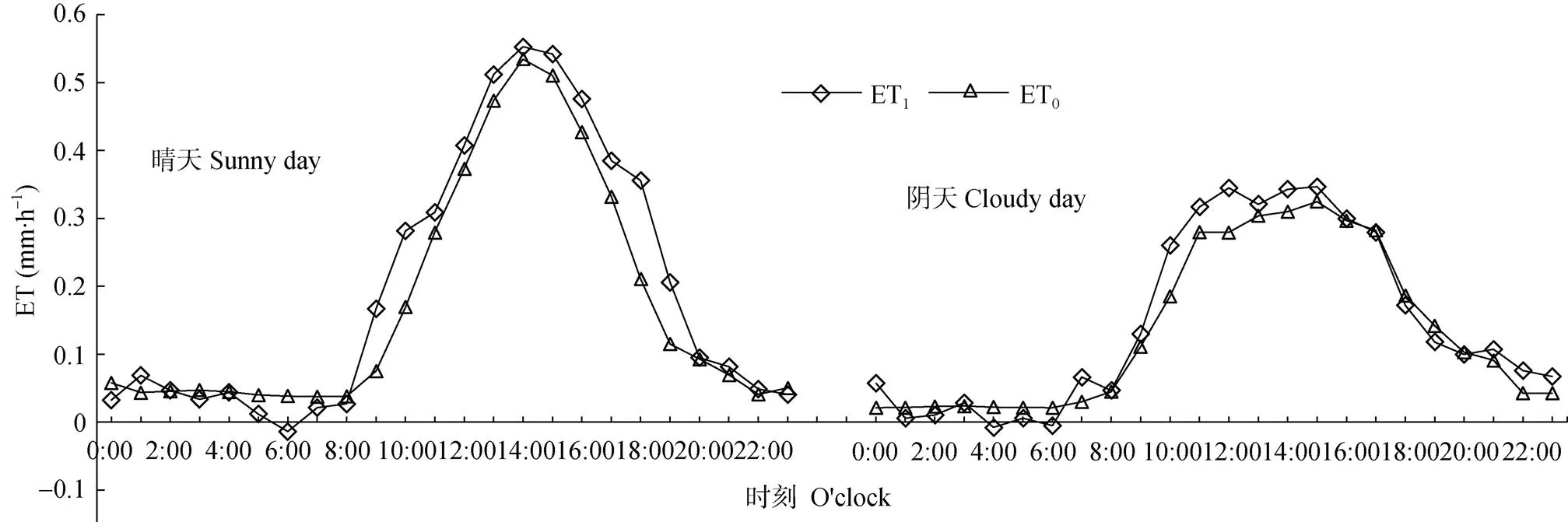
图1 枣树果实发育期典型天气腾发强度变化

ET1表示小时尺度下蒸渗仪实测腾发强度; ET0表示参考作物腾发强度。ET1is the measured evapotranspiration rate at hour scale by lysimeter; ET0is the reference crop evapotranspiration rare.

2 结果与分析

2.1 滴灌枣树典型日腾发特征

运用大型称重式蒸渗仪, 可以精确地刻画出枣树日内逐时腾发强度的变化趋势, 描述枣树日动态耗水特性。以ASCE-PM模型计算的小时尺度下ET0作为参考, 选取枣树2017年生长阶段具有代表性的晴天(8月14日)、阴天(8月17日)分析枣树逐时腾发强度(ET1)的动态变化, 两个时间均处于枣树果实发育期, 生长旺盛, 且期间只间隔3 d, 枣树生理指标的差异影响忽略不计。由枣树腾发强度变化(图1)可以看出, 枣树实际逐时腾发强度与ET0变化趋势基本一致, 二者日变化曲线均呈倒“U”型单峰变化; ET0相比枣树腾发强度曲线较为平滑。腾发强度从9:00左右开始增大, 14:00—16:00达到峰值。晴天枣树腾发强度峰值为0.55 mm∙h-1, 之后慢慢变小, 22:00开始在零附近变动, 且变化起伏较小; 阴天峰值相对晴天较不稳定, 12:00—16:00腾发强度较高; 阴天和晴天的夜间腾发强度都较小, 基本在0.05 mm∙h-1以内变动。枣树腾发强度均大于ET0, 主要是由于测定时间为枣树果实发育期, 枣树叶片、果实生长均较旺盛, 冠层幅度较大, 腾发强度大。晴天各时刻的枣树腾发强度值均大于阴天, 主要是晴天的太阳辐射和饱和水汽压差均大于阴天等因素引起的。枣树腾发作用主要发生在白天, 夜间也有腾发作用, 但较小, 值比较稳定。蒸渗仪测定晴天和阴天的腾发强度基本为正值,夜晚偶尔会有负值, 且阴天负值较多, 这主要是由于夜晚温度降低明显, 相对湿度增加, 空气中水分在作物叶面形成凝水珠, 从而增加了土体水重。

2.2 滴灌枣树各生育期腾发动态变化

由枣树逐日腾发强度动态变化图(图2)可知, 枣树耗水强度在各生育阶段的分配呈现出两头小、中间大的格局, 全生育期的日腾发强度总体趋势为前期缓慢增加, 至7月中旬左右达到最大, 随之进入下降阶段, 直至10月底成熟期结束。萌芽期枣树的腾发强度相对较小, 为2.70 mm∙d-1, 期间有两次灌水, 降雨与总灌溉量为68.5 mm。随着气温逐渐上升, 净辐射增强, 作物生长进入旺盛期, 叶面积指数增大, 植物蒸腾速率随之加强, 花期作物腾发强度增至4.42 mm∙d-1, 且花期在整个生育期中持续时间最长, 达56 d, 腾发总量为247.41 mm; 进入幼果期后, 腾发强度降至4.09 mm∙d-1, 这是由于幼果期时间较短, 仅有17 d, 且期间有5 d为降雨天气, 导致腾发速率较低; 进入果实发育期后, 人工灌水与降雨总量为127.4 mm, 停灌后, 棵间蒸发量减小, 腾发强度有所降低, 为3.81 mm∙d-1; 成熟期后, 枣树生长迟缓, 蒸腾作用减弱, 加之该阶段净辐射较弱, 气温减弱, 土壤蒸发量较小, 导致成熟期的腾发强度仅有1.40mm∙d-1。由此可见枣树不同生育期的耗水量差异较大, 枣树生长前期与末期耗水较少, 花期、幼果期、果实发育期的腾发强度较大。

灌溉环境及生长状况对作物耗水分布产生至关重要的影响, 表1为枣树不同生育阶段腾发特征情况。枣树从萌芽期到成熟期的腾发总量约为640.82 mm, 期间的降雨总量为99.20 mm, 仅为腾发量的14.86%, 全年灌水量为444.3 mm(含春灌30 mm), 其余97.32 mm枣树耗水为蒸渗仪土壤储水量。枣树作物系数在萌芽期至果实发育期呈现逐渐增大趋势, 由0.74增至1.13, 其中萌芽期至花期增率最大, 为31.01%, 成熟期下降至0.87。全生育期综合作物系数为0.94。枣树花期和果实发育期是持续时间最长的两个生育阶段, 达56 d与55 d之久, 且阶段腾发强度较大, 造成花期和果实发育期的需水量较大, 花期、幼果期和果实生长发育期相应各生育阶段的腾发量分别占总腾发量的38.61%、10.85%、32.72%。因此在制定滴灌枣树灌溉制度时, 在不影响植株正常生长的前提下, 应当优先保障枣树花期、幼果期和果实生长发育期的供水需求。

2.3 枣树腾发强度影响因素分析

在农田生态系统中, 作物腾发强度受众多因子影响, 而这些因子之间相互影响, 关系较复杂, 共同影响着农田系统的水汽收支。简单的相关系数不能够反映变量与腾发强度之间的关系, 众多的影响因子增加了预测腾发强度模型的复杂性与计算量, 为确保模型的稳定性, 综合全面考虑各因子, 剔除不显著因子, 以建立最优的回归模型。本研究分别以日和小时为时间尺度, 通过多元线性回归方法, 对蒸渗仪测得的枣树小时尺度下腾发强度(ET1)和日尺度下腾发强度(ET2)与叶面积指数(LAI)、冠层净辐射(n)、相对湿度(RH)、空气温度()、风速()和表层土壤含水率()等建立相关关系, 为不同时间尺度上的农田水分管理提供必要依据。

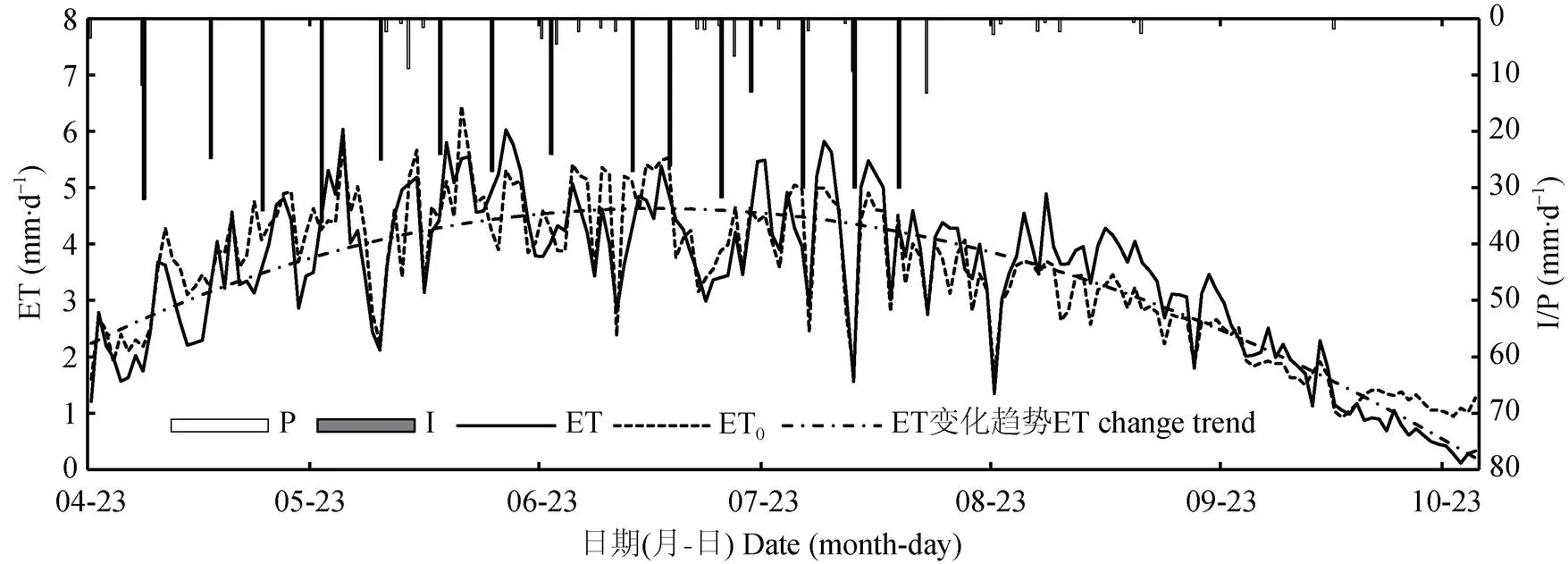
图2 枣树各生育期逐日腾发强度(ET)动态变化

P: 降水量; I: 灌水量; ET0: 作物参考腾发量。P: precipitation; I: irrigation; ET0: crop reference evapotranspiration.

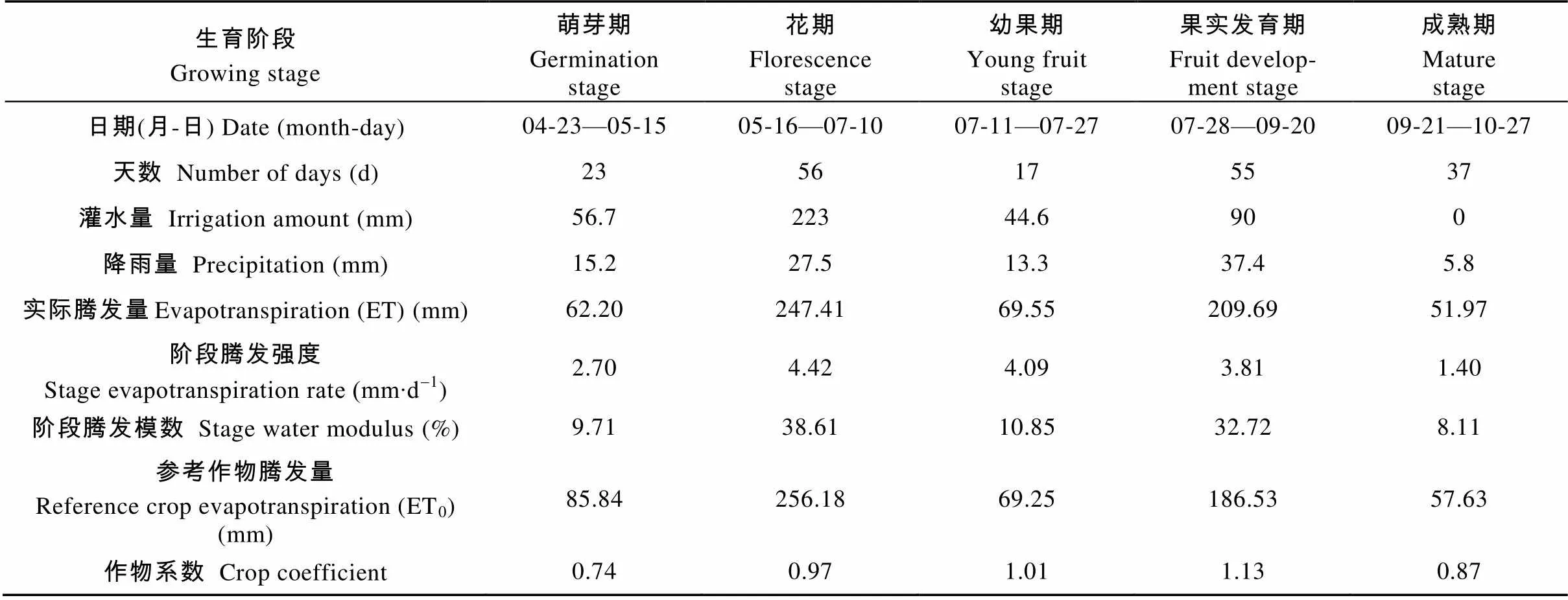
表1 枣树各生育阶段腾发及相关因素特征

2.3.1 不同时间尺度下相关关系分析

选取4月23日—7月10日(萌芽期、花期、幼果期), 对小时尺度下枣树腾发强度与影响因素的回归关系进行分析(表2), 方程置信度为<0.001, 复相关系数为0.853,统计值为394.36, 拟合度为0.721。进一步逐步线性回归分析可知, 回归方程的复相关系数和统计值均满足<0.001的要求, 方程极显著。其中相对湿度(RH)的显著性水平不满足回归系数检验≤0.05, 剔除该因子。由偏相关系数分析可知显著影响枣树腾发强度的因素依次为冠层净辐射(n)>空气温度()>风速()>叶面积指数(LAI)>表层土壤含水率(), 利用这些因子建立小时尺度下估算腾发强度模型为:

ET1(h)=0.153+0.004+0.012+0.176n+0.002+0.067LAI (3)

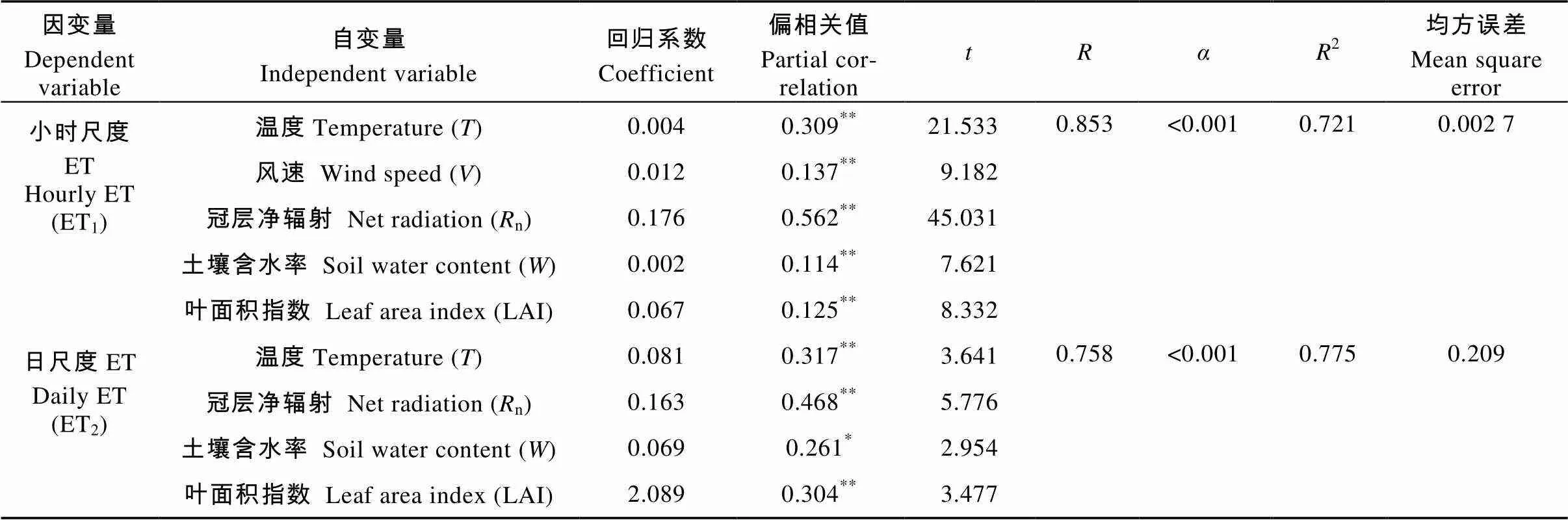
表2 不同时间尺度下腾发强度(ET)与各影响因子的回归关系检验

**为极显著相关, *为显著相关。** and * indicate extremely significant (< 0.01) and significant (< 0.05) correlations, respectively.

同样选取4月23日—7月27日(萌芽期、花期、幼果期), 进行日尺度下枣树腾发强度与影响因素的回归关系(表2), 分析方程置信度为<0.001水平, 复相关系数为0.758,统计值为40.235, 拟合度为0.775。进一步逐步线性回归分析可知, 回归方程的复相关系数和统计值均满足<0.001的要求, 方程极显著。在逐步回归分析中预测样本及验证样本的设定时, 相对湿度(RH)与风速()的显著性水平不满足回归系数检验≤0.05, 将这两个变量剔除。显著影响日尺度下腾发强度的相关因子主要是叶面积指数(LAI)、冠层净辐射(n)、空气温度()和表层土壤含水率()。各因子影响程度不同, 冠层净辐射(n)影响程度最大, 偏相关系数为0.468**; 腾发强度与表层土壤含水率()表现较弱的相关性, 偏相关系数仅为0.261*。杨光超等[15]研究玉米腾发强度也得出类似的研究成果。利用这些参数建立的日尺度下估算腾发强度模型为:

ET2(d)=-3.325+0.081+0.163n+0.069+2.089LAI (4)

2.3.2 不同时间尺度下枣树腾发强度模型预测

由于文章篇幅有限, 选取果实发育期(7月28— 31日)为代表展示蒸渗仪实测小时尺度下腾发强度与模型(3)模拟腾发强度的拟合关系(图3a), 其余时刻枣树果实发育期与成熟期的模型预测过程省略。将叶面积指数(LAI)、冠层净辐射(n)、空气温度()、风速()和表层土壤含水率()带入模型(3)。由图3a可以看出, 小时尺度下枣树实测与模拟腾发强度值对比, 二者变化趋势基本一致, 均呈现倒“U”型单峰变化趋势, 在峰值处普遍存在模拟值大于实测值的现象。实际测定结果在果实发育期和成熟期的腾发强度分别为0.158 mm∙h-1和0.060 mm∙h-1, 模拟值为0.159 mm∙h-1和0.062 mm∙h-1。说明模型(3)在果实发育期、成熟期均出现高估腾发强度的现象, 分别高估0.63%和3.33%。

选取果实发育期、成熟期(7月28日—10月27日)监测的叶面积指数(LAI)、冠层净辐射(n)、空气温度()和表层土壤含水率()带入模型(4), 预测枣树日尺度下腾发强度, 以蒸渗仪实测枣树腾发强度为基准检验模型(4)模拟值。图3b为日尺度下实测腾发强度与模型(4)模拟腾发强度的拟合图, 可以看出, 在果实发育期、成熟期实测与模拟腾发强度均呈逐渐下降趋势。以日为时间步长, 果实发育期和成熟期的实测腾发强度分别为3.798 mm∙d-1和1.434 mm∙d-1, 估算值为3.871 mm∙d-1和1.370 mm∙d-1。说明模型(4)高估了果实发育期腾发强度而低估了成熟期腾发强度, 其中果实发育期高估1.92%, 成熟期低估4.46%。

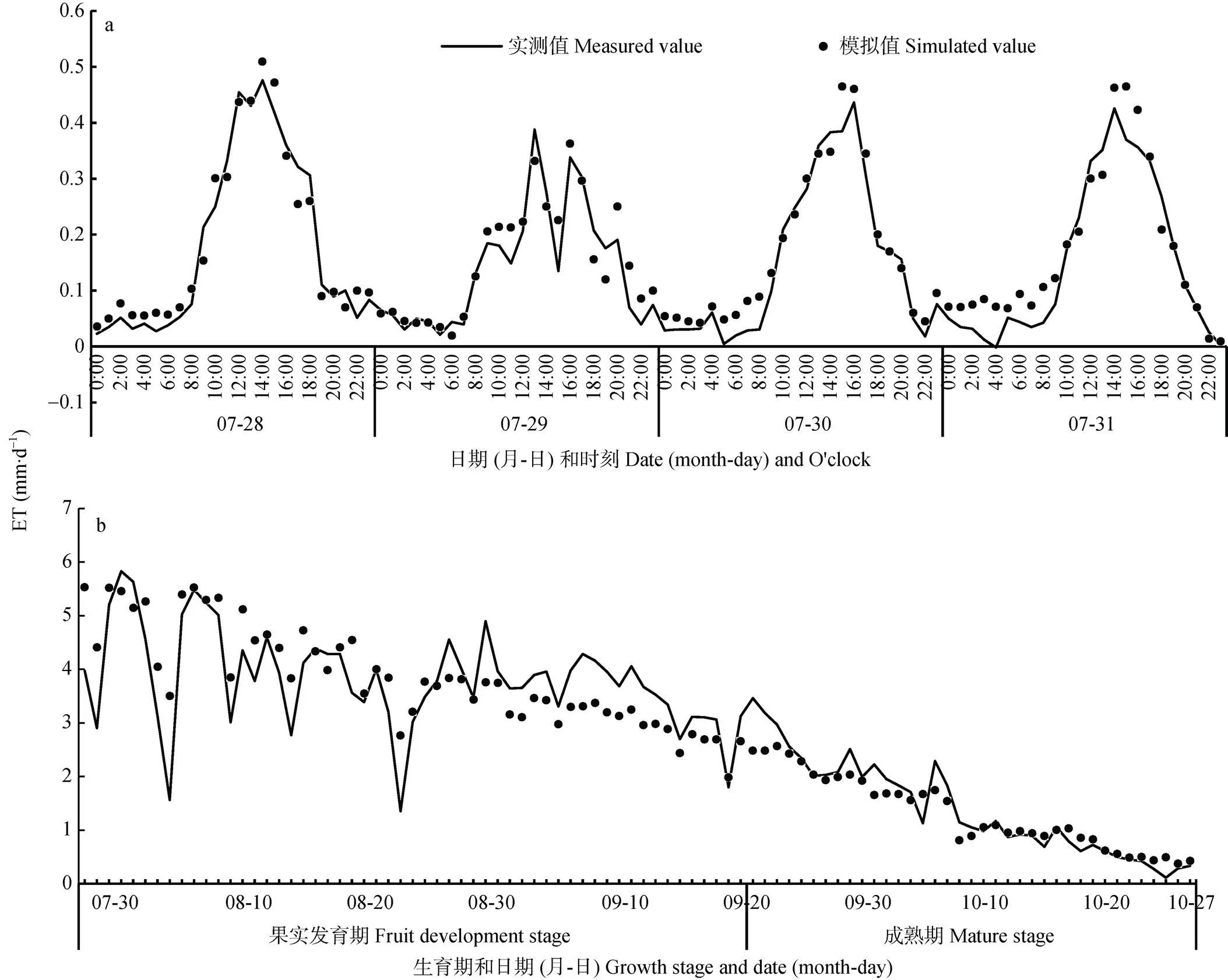
图3 枣树小时尺度(a)和日尺度(b)腾发强度(ET)模拟值和实测值的比较

2.3.3 不同时间尺度下枣树腾发模型误差分析

当以小时为步长, 模型(3)模拟腾发强度的、RMSE和NSE分别为0.784**、0.020 mm∙h-1和0.64, 果实发育期的误差大于成熟期, 且成熟期实测值与模拟值相关系数较高, 为0.796**。当以日为步长, 模型(4)估算枣树腾发强度的、RMSE和NSE分别为0.912**、0.362 mm∙d-1和0.81(表3)。与模型(3)相似, 模型(4)成熟期腾发强度估算值与模拟值较为接近, 两模型的误差分别为0.013 mm∙h-1、0.266 mm∙d-1, 拟合度也较高, 纳什效率系数分别达0.66、0.87, 与实测ET相关系数达0.937。从综合纳什效率来说, 模拟可信度较高的是模型(4), 纳什效率系数达0.81, 与蒸渗仪所测腾发强度值模拟误差最小。主要是因为当以小时为步长时, 土壤含水率测定值不稳定, 叶面积指数基本无变化, 且以小时为步长测定腾发强度值较小, 数值稍有波动对腾发强度的模拟值影响较大。

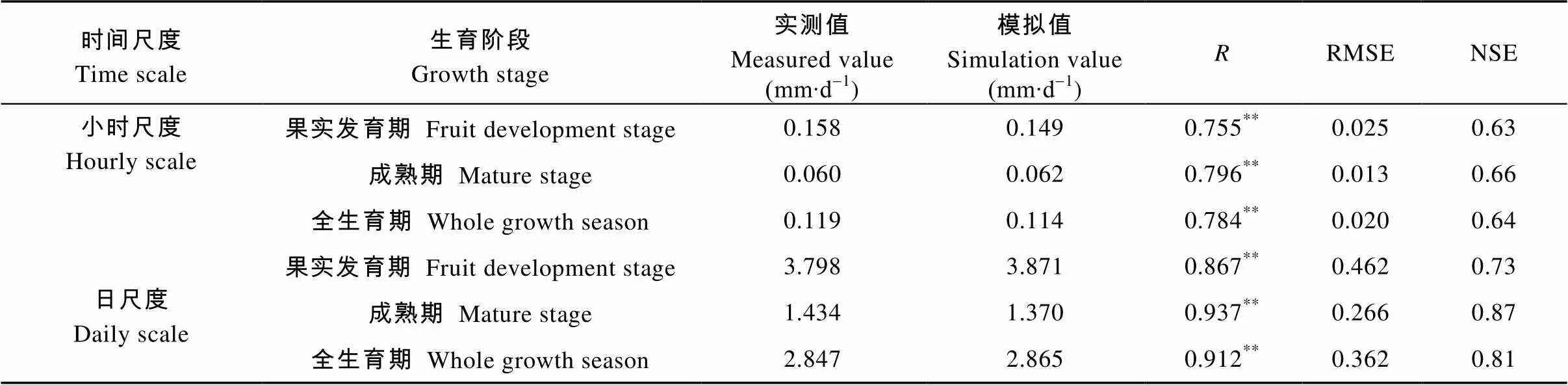
表3 枣树不同生育期估算不同时间尺度腾发强度(ET)误差分析

为复相关系数; RMSE为均方根误差; NSE为纳什效率系数。**为极显著相关(<0.01)。is complex correlation coefficient; RMSE is the root mean square error; NSE is the Nash efficiency coefficient. ** indicates extremely significant (< 0.01).

2.3.4 冠层净辐射对枣树腾发强度预测

通过考虑气象因素、叶面积指数、表层土壤含水量所建立的腾发强度估算模型精度较高, 但其所涉及的参数较多, 不便于在缺少数据支撑的前提下预测。辐射量作为腾发强度的驱动因子, 经检验分析, 在以小时、日为步长计算腾发强度时, 冠层净辐射量(n)是两种尺度上枣树腾发强度最主要的影响因素。为了简化作物腾发强度的估算, 以枣树全生育期冠层净辐射量与腾发强度数据为基础, 对二者做相关关系分析。结果表明, 二项式拟合度最高(图4), 两种时间步长计算出的腾发强度与n均呈较好的相关性, 以小时和日为步长下,n与腾发强度相关系数分别为0.862**和0.841**。

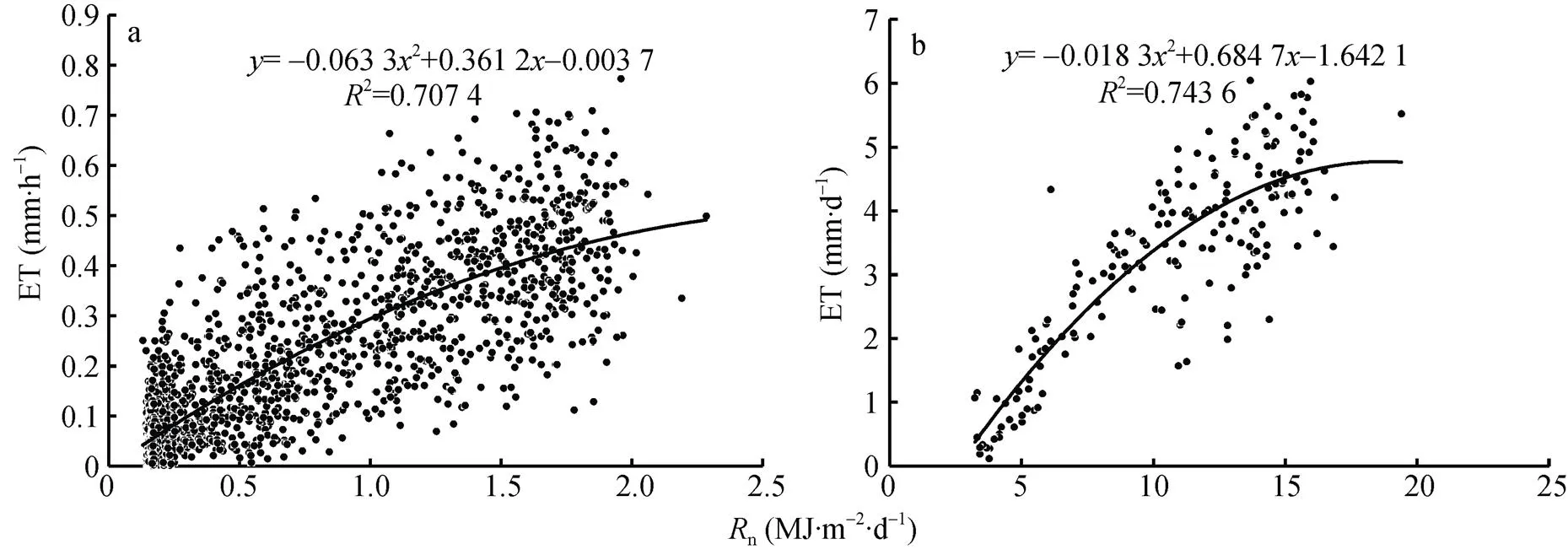
图4 小时尺度(a)和日尺度(b)下枣树冠层净辐射(Rn)与腾发强度(ET)的关系

3 讨论

对于果树腾发量、需水量的研究, 国内外学者已有不少成果[22-24], 大多确定枣树腾发量测量的时间为一个灌水周期, 间隔较长, 且随着灌水结束, 后期测量结束, 造成数据量少且测定周期不完整现象。蒸渗仪可自动监测枣树全年逐时腾发强度, 数据完整精确, 代表性强。根据本研究大型称重式蒸渗仪得出滴灌枣树果实发育期不同天气腾发强度测定结果表明, 农田的耗水量随着天气变化而变化。晴天表现为明显的单峰变化趋势, 峰值在14:00—16:00, 阴天12:00—16:00时段明显高于一天中其他时段。不论晴天、阴天, 农田腾发过程主要发生在10:00—20:00, 其他时段在零附近变动, 腾发强度贡献率极小。本地区晴天腾发高峰在14:00—16:00, 这与王文明等[25]在新疆和田干旱荒漠性气候区测定枣树最大径流在中午14:00前后出现结果类似, 而与甘卓亭等[26]在黄土塬区测定麦田腾发高峰期在11:00—14:00存在差异, 这主要是由于地区气候、时差不同造成的。枣树花期、果实发育期占全生育期腾发量的38.61%、32.72%, 这与王则玉等[7]确定开花坐果期与果实膨大期是枣树需水关键期结论类似。这些结论将有助于加深对本气候区的枣树腾发机制认识, 且观测结果为率定和校验其他方法提供可靠的科学依据[27-29]。腾发强度受多种因素影响, 不同气象水平年下腾发量值不同, 本文所确定的2017年枣树腾发量640.83 mm为单一值, 不是区间值。为确定更加严谨准确的枣树腾发量值, 应结合多年枣树腾发量值分析, 进一步确定枣树腾发量区间与年季变化趋势。作物系数分析较简单, 可结合下一年数据补充另行分析。

作物腾发强度不仅受自身生理影响, 同时受环境、气象因子影响。对于气象、作物、土壤等因素对腾发强度影响的研究已有不少成果。而本文在小时和日时间尺度上, 影响滴灌枣树腾发强度的主要因素并不完全相同, 影响程度也不相同。其中风速()仅为小时尺度下腾发强度的影响因子, 主要是由于以小时为步长时, 风速变化较明显; 而叶面积指数(LAI)与表层土壤含水率()对腾发强度影响较小, 这主要是叶面积指数(LAI)与表层土壤含水率()逐时变化幅度太小。在不同时间尺度下腾发强度与冠层净辐射(n)相关关系均较好, 与其他因素的相关关系随时间尺度变化而变化。这与刘国水等[30]对日尺度下影响腾发强度的研究结果一致, 而与强小嫚等[31]分析表明蒸渗仪实测值日变化和太阳净辐射日变化的关系不很明显不同, 亦与刘笑吟等[32]得出日尺度下对土壤蒸发和植株蒸腾影响最显著的因子分别是叶面积指数与净辐射, 小时尺度下对土壤蒸发和植株蒸腾影响最显著的因子分别是叶面积指数与饱和水汽压差的结果有所差异。主要原因是本文基于作物总腾发强度, 而前者测定的是土壤蒸发与植株蒸腾两方面, 且两个试验区气候有所不同。本文建立不同时间尺度下预测腾发强度的模型(3)、(4)的基础数据为枣树萌芽期、花期、幼果期的数据, 其余时段数据用于模型检验, 由于数据量不足, 模型的拟合度不高, 可结合下一年的数据对模型进行优化并检验, 以建立可信度更高的腾发强度预测模型。

4 结论

1)滴灌枣树腾发强度日内逐时变化曲线呈单峰型, 腾发强度基本从9:00左右开始增大, 中午14:00—16:00达到峰值, 之后慢慢变小, 至22:00左右在零附近变动, 夜间水汽凝结导致偶有负值出现。

2)枣树全生育期逐日腾发强度动态变化呈先增大后减小的趋势, 高峰期出现在花期后期、幼果期、果实发育期前期, 枣树从萌芽期到成熟期的腾发总量约为640.83 mm, 其中花期和果实发育期占全生育期腾发量的38.61%和32.72%, 需水量占比较大。

3)在小时和日时间尺度上, 影响滴灌枣树腾发强度的主要因素不完全相同, 影响程度也不相同, 存在明显的时间尺度差异。但在不同时间尺度下腾发强度与冠层净辐射量(n)相关性较强, 与其他因素的相关关系随时间尺度变化而变化。本文综合考虑各影响腾发强度因素所建立的模型ET1(h)=0.153+0.004+0.012+0.176n+0.002+0.067LAI和ET2(d)=-3.325+0.081+0.163n+0.069+ 2.089LAI的精确度高, 可满足精准灌溉要求下的需水量估算, 仅考虑净辐射建立的模型ET1(h)=-0.063 3n2+0.361 2n−0.003 7和ET2(d)=-0.018 3n2+ 0.684 7n–1.642 1可用于不同时间尺度、缺少数据支撑下的需水量估算, 为阿克苏地区滴灌枣树腾发强度预测提供理论支持。

[1] 赵华, 申双和, 华荣强, 等. Penman-Monteith模型中水稻冠层阻力的模拟[J]. 中国农业气象, 2015, 36(1): 17–23 ZHAO H, SHEN S H, HUA R Q, et al. Simulation of canopy resistance for paddy rice based on Penman-Monteith model[J]. Chinese Journal of Agrometeorology, 2015, 36(1): 17–23

[2] 郑珍, 蔡焕杰, 虞连玉, 等. CERES-Wheat模型中两种蒸发蒸腾量估算方法比较研究[J]. 农业机械学报, 2016, 47(8): 179–191 ZHENG Z, CAI H J, YU L Y, et al. Comparison of two crop evapotranspiration calculating approaches in CSM-CERES- Wheat model[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(8): 179–191

[3] JI J M, CAI H J, HE J Q, et al. Performance evaluation of CERES-Wheat model in Guanzhong Plain of Northwest China[J]. Agricultural Water Management, 2014, 144: 1–10

[4] HE J Q, CAI H J, BAI J P. Irrigation scheduling based on CERES-Wheat model for spring wheat production in the Minqin Oasis in Northwest China[J]. Agricultural Water Management, 2013, 128: 19–31

[5] 郑强卿, 陈奇凌, 李铭, 等. 南疆枣树种植模式改造对骏枣生长发育的影响[J]. 西南农业学报, 2015, 28(4): 1564–1568 ZHENG Q Q, CHEN Q L, LI M, et al. Effect of cultivation mode on growth and development of Jun-jujube from south of Xinjiang[J]. Southwest China Journal of Agricultural Sciences, 2015, 28(4): 1564–1568

[6] 马建鹏, 董建国, 汪有科, 等. 黄土丘陵区枣林地土壤水分时空变化研究[J]. 中国生态农业学报, 2015, 23(7): 851–859 MA J P, DONG J G, WANG Y K, et al. Temporal and spatial variations in soil moisture under jujube forests in the loess hilly region[J]. Chinese Journal of Eco-Agriculture, 2015, 23(7): 851–859

[7] 王则玉, 谢香文, 刘国宏, 等. 干旱区绿洲滴灌成龄枣树耗水规律及作物系数[J]. 新疆农业科学, 2015, 52(4): 675–680 WANG Z Y, XIE X W, LIU G H, et al. Jujube drip irrigation water consumption and its crop coefficient in oasis of arid areas[J]. Xinjiang Agricultural Sciences, 2015, 52(4): 675–680

[8] 曹俊. 陕北山地微灌土壤水分入渗特性与枣树耗水规律试验研究[D]. 西安: 西安理工大学, 2010: 52–70CAO J. Study on the characteristics of mico-irrigation soil water infiltration and jujube of water-consuming law in northern Shaanxi mountain[D]. Xi’an: Xi’an University of Technology, 2010: 52–70

[9] 王怡宁, 朱月灵. 蒸渗仪国内外应用现状及研究趋势[J]. 水文, 2018, 38(1): 81–85 WANG Y N, ZHU Y L. Application status and research trend of domestic and foreign Lysimeter[J]. Journal of China Hydrology, 2018, 38(1): 81–85

[10] KNAPPE S, HAFERKORN U, MATTUSCH J, et al. Water and solute balances in recultivated lignite mining dump soils-field data and lysimeter experiments[J]. Water Air and Soil Pollution, 2004, 157(1/4): 85–105

[11] 刘晓英, 李玉中, 钟秀丽, 等. 基于称重式蒸渗仪实测日值评价16种参考作物蒸散量(ET0)模型[J]. 中国农业气象, 2017, 38(5): 278–291 LIU X Y, LI Y Z, ZHONG X L, et al. Evaluation of 16 models for reference crop evapotranspiration (ET0) based on daily values of weighing lysimeter measurements[J]. Chinese Journal of Agrometeorology, 2017, 38(5): 278–291

[12] 张乐昕, 丛振涛. 基于FAO-Blaney-Criddle方法的河套灌区参考作物蒸散发量估算[J]. 农业工程学报, 2016, 32(16): 95–101 ZHANG L X, CONG Z T. Calculation of reference evapotranspiration based on FAO-Blaney-Criddle method in Hetao irrigation district[J]. Transactions of the CSAE, 2016, 32(16): 95–101

[13] 黄仲冬, 齐学斌, 樊向阳, 等. 土壤水分有效性及其影响因素定量分析[J]. 水土保持学报, 2014, 28(5): 71–76 HUANG Z D, QI X B, FAN X Y, et al. Quantitative analysis of soil water availability and its influencing factors[J]. Journal of Soil and Water Conservation, 2014, 28(5): 71–76

[14] 汪秀敏, 申双和, 韩晓梅, 等. 大型称重式蒸渗仪测定的冬小麦农田的蒸散规律研究[J]. 气象与环境科学, 2011, 34(4): 14–18 WANG X M, SHEN S H, HAN X M, et al. Study on evapotranspiration of the winter wheat measured by large-scale weighting lysimeter[J]. Meteorological and Environmental Sciences, 2011, 34(4): 14–18

[15] 杨光超, 朱忠礼, 谭磊, 等. 怀来地区蒸渗仪测定玉米田蒸散发分析[J]. 高原气象, 2015, 34(4): 1095–1106 YANG G C, ZHU Z L, TAN L, et al. Analysis on evapotranspiration of maize field measured by lysimetersin in Huailai[J]. Plateau Meteorology, 2015, 34(4): 1095–1106

[16] 洪明, 朱航威, 穆哈西, 等. 不同滴头流量及灌水定额下红枣树耗水规律[J]. 干旱地区农业研究, 2014, 32(1): 72–77HONG M, ZHU H W, MU H X, et al. The water consumption rule of jujube trees under different emitter flow rate and irrigation quota[J]. Agricultural Research in the Arid Areas, 2014, 32(1): 72–77

[17] ALLAN R G, PEREIRA L S, RAES D, et al. Crop evapotranspiration-guidelines for computing crop water requirements-FAO irrigation and drainage paper 56[R]. Rome: FAO, 1998: 56

[18] DING R S, KANG S Z, LI F S, et al. Evaluating eddy covariance method by large-scale weighing lysimeter in a maize field of northwest China[J]. Agricultural Water Management, 2010, 98(1): 87–95

[19] 季辰, 朱忠礼, 徐自为. 高精度称量式蒸渗仪数据处理方法研究[J]. 北京师范大学学报: 自然科学版, 2016, 52(5): 628–634 JI C, ZHU Z L, XU Z W. Data processing of high precision weighing lysimeter[J]. Journal of Beijing Normal University: Natural Science, 2016, 52(5): 628–634

[20] ALLEN R G, WALTER I A, ELLIOTT R L, et al. The ASCE standardized reference evapotranspiration equation[R]. Reston: American Society of Civil Engineers, 2005

[21] ITENFISU D, ELLIOTT R L, ALLEN R G, et al. Comparison of reference evapotranspiration calculations as part of the ASCE standardization effort[J]. Journal of Irrigation and Drainage Engineering, 2003, 129(6): 440–448

[22] 孙发政. 水土生态的理论与实践[J]. 中国水土保持, 2017, (12): 14–17 SUN F Z. The theory and practice of soil and water ecology[J]. Soil and Water Conservation in China, 2017, (12): 14–17

[23] 卫新东, 刘守阳, 陈滇豫, 等. Shuttleworth-Wallace模型模拟陕北枣林蒸散适用性分析[J]. 农业机械学报, 2015, 46(3): 142–151 WEI X D, LIU S Y, CHEN D Y, et al. Applicability of Shuttleworth-Wallace model for evapotranspiration estimation of jujube forests in Loess Hilly-gully region[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(3): 142–151

[24] 白永红, 高志永, 汪有科, 等. 修剪强度对枣林地耗水及水分利用效率的影响[J]. 水土保持研究, 2018, 25(4): 206–214 BAI Y H, GAO Z Y, WANG Y K, et al. Effects of pruning intensity on water consumption and water use efficiency of jujube plantation[J]. Soil and Water Conservation Research, 2018, 25(4): 206–214

[25] 王文明, 郑德明, 姜益娟, 等. 滴灌条件下枣树耗水规律的研究[J]. 干旱地区农业研究, 2014, 32(6): 38–42 WANG W M, ZHENG D M, JANG Y J, et al. Research on water consumption rule of jujube tree under drop irrigation[J]. Agricultural Research in the Arid Areas, 2014, 32(6): 38–42

[26] 甘卓亭, 刘文兆. 黄土塬区麦田蒸散特征[J]. 应用生态学报, 2006, 17(8): 1435–1438 GAN Z T, LIU W Z. Evapotranspiration of winter wheat field on Loess Plateau tableland[J]. Chinese Journal of Applied Ecology, 2006, 17(8): 1435–1438

[27] 李杰, 吴杨焕, 陈锐, 等. 基于大型称重式蒸渗仪研究北疆滴灌麦田蒸散量[J]. 作物学报, 2016, 42(7): 1058–1066 LI J, WU Y H, CHEN R, et al. Measurement of evapotranspiration for drip-irrigated winter wheat using large weighing lysimeter in northern Xinjiang[J]. Acta Agronomica Sinica, 2016, 42(7): 1058–1066

[28] 王晓晨, 朱忠礼, 季辰, 等. 几种蒸散计算方法在怀来地区的适用性研究[J]. 气象, 2016, 42(11): 1395–1401 WANG X C, ZHU Z L, JI C, et al. Applicability of evapotranspiration estimation methods in the Huailai region of Hebei Province[J]. Meteorological Monthly, 2016, 42(11): 1395–1401

[29] WEI Z, LIU Y, XU D, et al. Evapotranspiration and ratio of soil evaporation to evapotranspiration of winter wheat and maize[J]. Applied Mechanics and Materials, 2014, 539: 832–837

[30] 刘国水, 刘钰, 蔡甲冰, 等. 农田不同尺度蒸散量的尺度效应与气象因子的关系[J]. 水利学报, 2011, 42(3): 284–289LIU G S LIU Y, CAI J B, et al. Study on scale effect of farmland evapotranspiration and relationship with meteorological factors[J]. Journal of Hydraulic Engineering, 2011, 42(3): 284–289

[31] 强小嫚, 蔡焕杰, 王健. 波文比仪与蒸渗仪测定作物蒸发蒸腾量对比[J]. 农业工程学报, 2009, 25(2): 12–17 QIANG X M, CAI H J, WANG J. Comparative study of crop evapotranspiration measured by Bowen ratio and lysimeter[J]. Transactions of the CSAE, 2009, 25(2): 12–17

[32] 刘笑吟, 王冠依, 杨士红, 等. 不同时间尺度节水灌溉水稻腾发量特征与影响因素分析[J]. 农业机械学报, 2016, 47(8): 91–100 LIU X Y, WANG G Y, YANG S H, et al. Influence factors and characteristics of transpiration and evaporation in water-saving irrigation paddy field under different temporal scales[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(8): 91–100

Prediction of the evapotranspiration rate of jujube using lysimeters for drip irrigation*

GUO Dandan, MA Yingjie, MA Liang**

(School of Water Conservancy and Civil Engineering, Xinjiang Agricultural University, Urumqi 830052, China)

Measuring field evapotranspiration can provide important information needed for estimating soil moisture and crop water stress and premature drying out, and such information is essential for irrigation formulation. Evapotranspiration can be measured using large lysimeters that have the advantage of confining soil boundaries, flexible measuring intervals, and high precision. Most of studies of evapotranspiration have been done for annual crops such as wheat and maize, and the present study was conducted to measure evapotranspiration of jujubes. Jujube trees of four years were transplanted into lysimeters and evapotranspiration was measured at 30-min intervals for complete growth season. The correlation between evapotranspiration rate and leaf area index, meteorological factors, and surface soil moisture content was analyzed based on water balance and the PM formula. The daily evapotranspiration of jujube was unimodal, taking place mainly in the daytime; the contribution of was small and stable. Evapotranspiration peaked at flowering stage, reaching 4.42 mm∙d-1, and then declined gradually. The total evapotranspiration during growth season was 640.83 mm, a large proportion of which occurred during flowering and fruit development stages that accounted for 38.61% and 32.72%, respectively. The observation suggested that there is a need for flowering and fruit stages to be emphasized in irrigation of jujube trees. Hourly and daily evapotranspiration rates of jujube were different in their affecting factors. The wind speed () affected hourly evapotranspiration only. The most sensitive factor for evapotranspiration was canopy net radiation (n), followed by air temperature (), wind speed (), leaf area index (LAI), and surface soil moisture content (W), as summarized in the following empirical equations for hourly and daily evapotranspiration, respectively: ET1(h) = 0.153 + 0.004+ 0.012+ 0.176n+ 0.002+ 0.067LAI, and ET2(d) =-3.325 + 0.081+ 0.163n+ 0.069+ 2.089LAI. Because canopy net radiation had the largest and most significant impact (the partial correlation coefficient was 0.562**and 0.468**for the hourly and daily equation, respectively), the regression was simplified as ET1(h) = 0.232 6n+ 0.018,2= 0.719 6, and ET2(d) = 0.321 2n− 0.141 8,2=0.719 6. These equations were tested to be accurate and could be used to estimate the evapotranspiration rate of jujube for developing drip irrigation in arid areas when input data were complete or partially complete.

Evapotranspiration rate; Meteorological factors; Time scale; Jujube; Drip irrigation

, E-mail: 42409584@qq.com

Jun. 4, 2018;

Nov. 29, 2018

S271

A

2096-6237(2019)03-0474-10

10.13930/j.cnki.cjea.180529

郭丹丹, 马英杰, 马亮. 蒸渗仪测定滴灌枣树不同时间尺度下腾发强度特征[J]. 中国生态农业学报(中英文), 2019, 27(3): 474-483

GUO D D, MA Y J, MA L. Prediction of the evapotranspiration rate of jujube using lysimeters for drip irrigation[J]. Chinese Journal of Eco-Agriculture, 2019, 27(3): 474-483

* 国家自然科学基金项目(51369029)、水利工程重点学科基金项目(SLXK2018-01)、干旱区枣树节水调质技术及智能决策系统研发创新团队(XJEDU2017T004)及新疆水利科技项目(2017G04)资助

马亮, 主要从事节水灌溉理论研究。E-mail: 42409584@qq.com

郭丹丹, 主要从事节水灌溉理论研究。E-mail: 623046780@qq.com

2018-06-04

2018-11-29

* This study was funded by the National Natural Science Foundation of China (51369029), the Key Discipline Fund Project of Water Conservancy Engineering (SLXK2018-01), the Innovation Team of Jujube Water Saving and Quality Control Technology (XJEDU2017T004) and the Xinjiang Water ConservancyScience and Technology Project (2017G04).