六支链轮腿式月面机器人机构优化设计

李 聪，韩亮亮，袁 帅，张元勋

(1. 上海宇航系统工程研究所，上海 201108； 2. 上海市空间飞行器机构重点实验室，上海 201108； 3. 重庆大学 机械工程学院，重庆 400044； 4. 南京航空航天大学航天学院， 南京 210016)

1 引言

月球是人类开展深空探测的起点，而月面机器人将在月球探测活动中扮演着至关重要的角色[1]。月球的主要地形有环山、月海、月陆和山脉等，月面机器人要在此环境中作业就必须具备一定的越障能力。目前月面机器人行走方式主要有轮式、腿式、履带式以及复合式[2]，其中轮腿复合式移动机构融合了轮式移动机构高速高效及腿式移动机构复杂地形适应能力强的优点，但机构相对复杂、移动性能参数在不同构型状态下有所变化。因此，有必要开展轮腿式机器人构型尺寸及可调构型参数与运动性能关系的研究，以获取更优的运动性能。

目前针对轮腿式月面机器人机构的研究多在构型设计、步态规划等方面，在轮式移动性能构型优化方面的研究尚较少。本文针对此问题，以六支链轮腿式月面机器人为研究对象，以机器人爬坡这一典型越障工况为输入条件，通过ADAMS建立参数化分析模型，研究轮腿尺寸参数与腿部角度与爬坡驱动力的关系，优化配置参数。

2 六支链轮腿式月面机器人

轮腿式月面机器人可抽象为悬架、轮腿和车身三部分[3-4]，构型为在六个方向上都具有对称结构的正六边形布局，在传统三个自由度之外另有一个转动副，可使车轮能绕着上一关节整周旋转。六支链轮腿机构构型及组成如图1所示，其单腿机构构型及组成如图2所示。

图1 六支链轮腿式月面机器人机构示意图Fig.1 Schematic diagram of six branched wheel-legged lunar robots

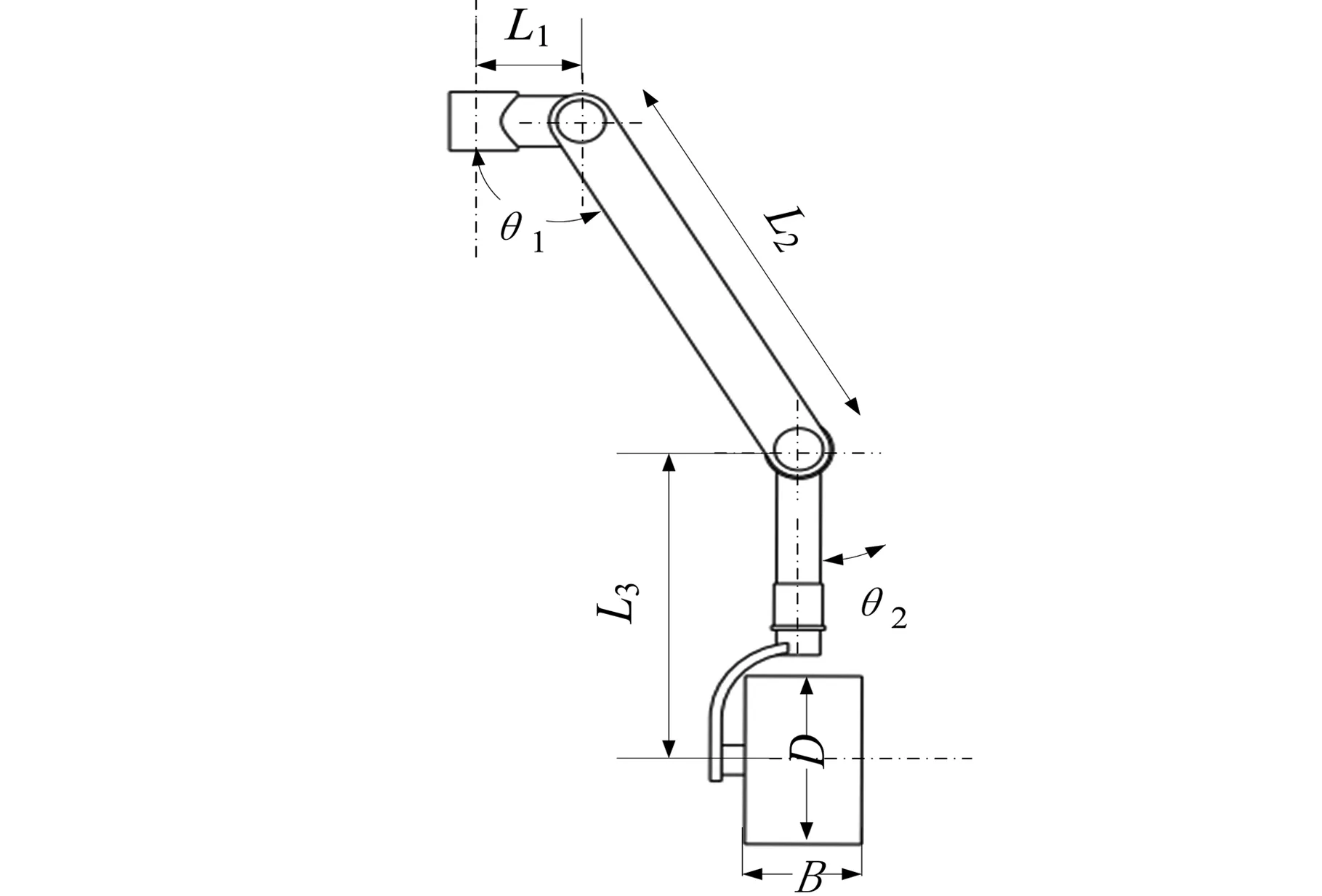
图2 机器人轮腿机构简图Fig.2 Sketch of the mechanism of the robot wheel leg

3 参数化模型

建立六支链轮腿式月面机器人单腿结构及坐标系如图3所示，单腿初始位置设置为腰关节轴线J1与车身上下平面垂直，大腿垂直向下，小腿轴线J4与J1平行，车轮朝向前进方向。腿部建立的四个坐标系分别为基坐标系Oxyz、髋关节坐标系O1x1y1z1、膝关节坐标系O2x2y2z2、踝关节坐标系O3x3y3z3以及轮腿末端坐标系O4x4y4z4。

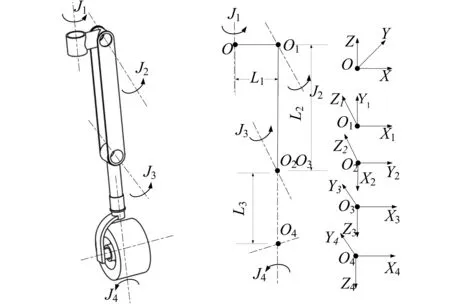
图3 机器人腿部坐标系建立示意图Fig.3 Schematic diagram of the robot's leg coordinate system

根据所建立的机器人腿部坐标系、设定的轮腿杆长及关节角数据得出六支链轮腿式月面机器人腿部D-H参数表(表1)。

表1 机器人腿部D-H参数表

六支链轮腿式月面机器在斜坡上移动的受力情况可简化如图4所示。定义正六边形车身的外接圆直径为D0，则机器人初始状态轮腿分布如图5所示，其中β为机器人大腿分布角，图中为60°，V为速度。

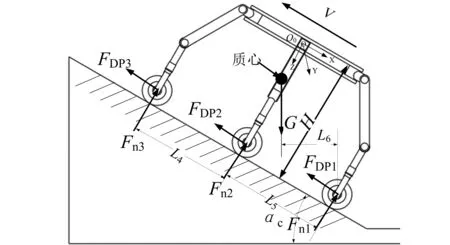
图4 机器人坡面行驶受力示意图Fig.4 Schematic diagram of the force on the slope of the robot

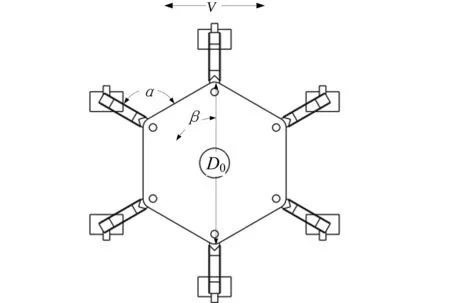
图5 六支链轮腿式月面机器人爬坡位姿示意图Fig.5 Schematic diagram of the climbing posture of Six branched wheel-legged lunar robot

由图1易知机器人质心坐标X=Y=0。假设六支链轮腿式月面机器人各组成部分质量均匀，可定义车身与腰关节与髋关节以及髋节的质量为G1，大腿质量为G2，膝关节与小腿与踝关节与踝节质量为G3，车轮质量为G4。令G1位于车身坐标原点，大腿质心位于其几何中心位置，G3位于小腿长度中心位置处，G4位于车轮轴心位置。则可知六支链轮腿式月面机器人在图5状态下质心Zc的坐标为式(1)：

(1)

定义爬坡中后轮轮心指向质心为一观测向量，则观测向量在水平面上的投影方向与爬坡速度方向相同时，即为六支链轮腿式月面机器人爬坡时不产生倾覆的必要条件，即L6≥0推导可得六支链轮腿式月面机器人爬坡不倾覆的必要条件为式(2)：

(2)

由式(2)可知轮腿杆长及关节角是影响六支链轮腿式月面机器人爬坡稳定性的主要变量。

4 仿真优化

轮式月面机器人的爬坡能力一般优于20°，因此本文六支链轮腿式月面机器人以爬30°斜坡作为计算工况，根据式(2)中的设计变量，通过ADAMS对六支链轮腿式月面机器人进行参数分析与优化。

根据月面机器人初始设计参数设定参数化模型的初始值L2为490 mm、L3为350 mm、θ1为0°，由于小腿轴线与车身轴线平行，故小腿的俯仰角θ2与大腿的俯仰角θ1关系为θ2=θ1-90°。通过对点的参数化实现对六支链轮腿式月面的机器人大腿长度L2、小腿长度L1、小腿俯仰角θ2的参数化。其它机器人参数按照设计值设置如表2所示。在ADAMS的优化设计中以驱动力最小为优化目标，由于机器人爬坡过程中后轮受力最大，如图6所示，故以机器人后车轮转矩为优化对象。

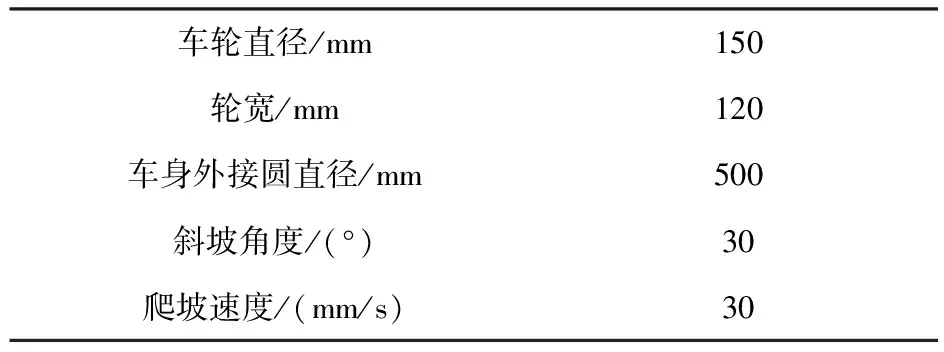
表2 仿真模型参数设置

在ADAMS中运行“设计研究”，即设计变量只有一个在其变化范围内取不同值时，目标函数的变化情况[7]。分析设计变量大腿长度(图7中ARM1_2Z)、小腿长度(图7中xt_l)、小腿俯仰角(图8中DV_1)的参数化对目标函数的灵敏度，可知所设置的设计变量对六支链轮腿式月面机器人后轮驱动力有较高的灵敏度，在机器人的设计与控制中应重点关注。

图6 机器人爬坡中前轮与后轮转矩曲线图Fig.6 Torque curve of front and rear wheels in the climbing robot

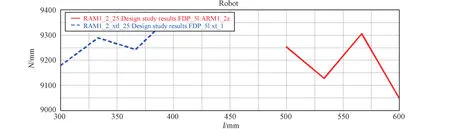
图7 设计变量ARM1_2Z及xt_l对目标函数的敏感度曲线图Fig.7 Sensitivity curve of design variables ARM1_2Z and xt_l to the objective function

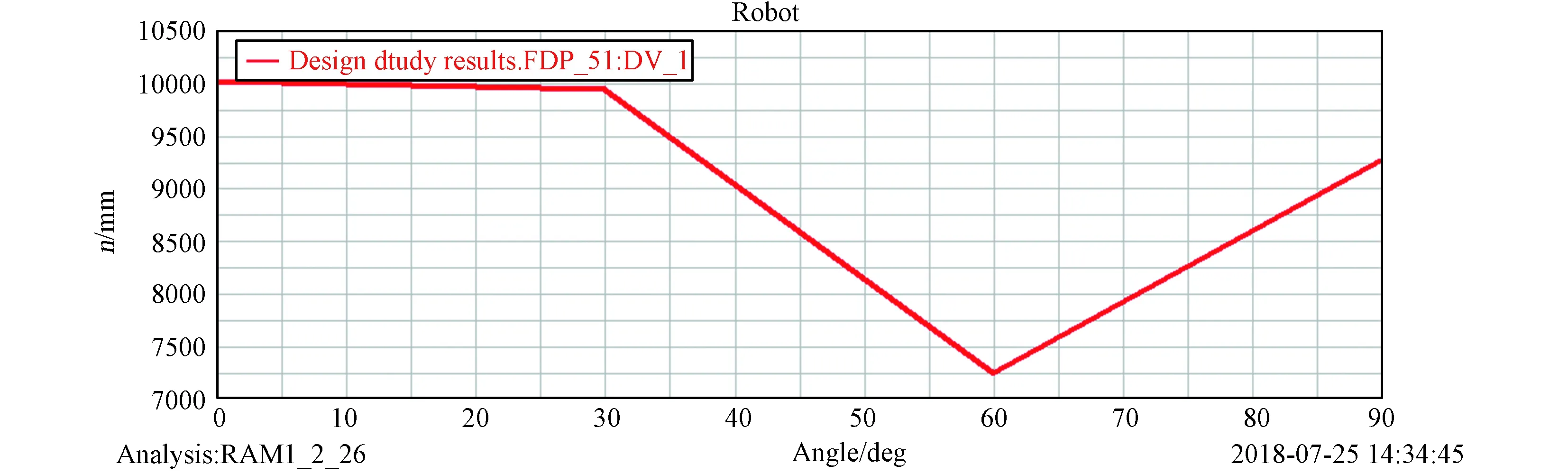
图8 设计变量DV_1对目标函数敏感度曲线图Fig.8 Sensitivity curve of design variables DV_1 to the objective function

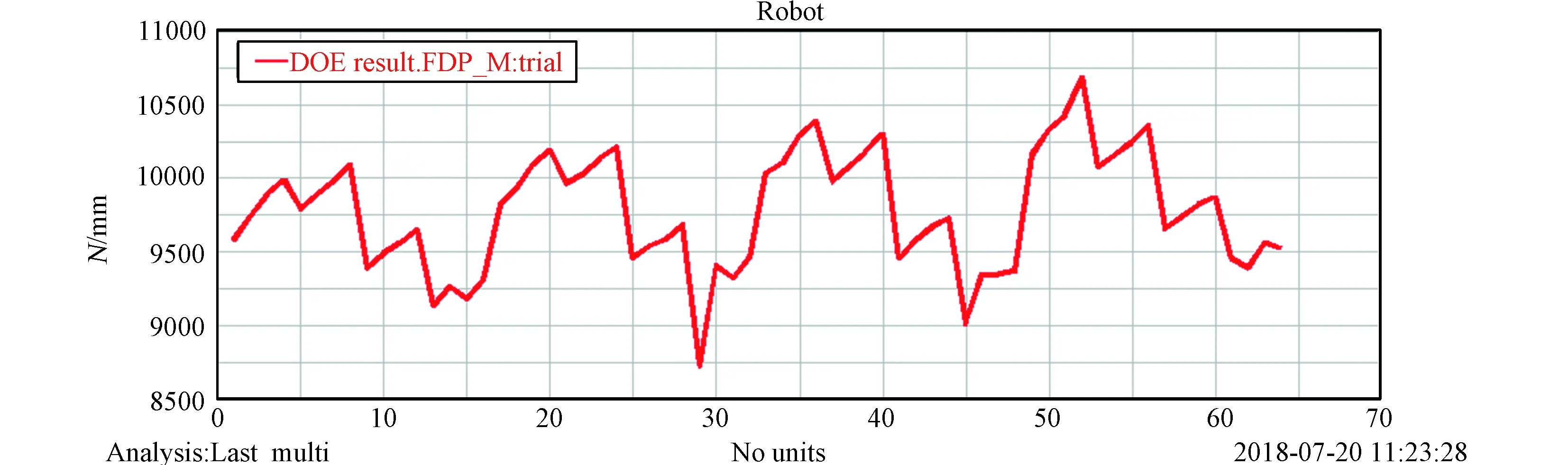
图9 目标函数值与迭代次数曲线图(横坐标为迭代次数、纵坐标为转矩)Fig.9 Graph of objective function value and iteration number

优化分析前先进行“实验设计”，即研究设计变量取不同的可能组合时目标函数的取值情况[7]，结果如图9所示，其最优结果对应的设计变量为大腿最优长度为486 mm、小腿长度为314 mm、大腿俯仰角为90°，此时大腿平行于车身，小腿垂直于大腿，此时机器人爬坡的状态如图10所示。

图10 六支链轮腿式月面机器人最优解下姿态Fig.10 Attitude of the optimal solution of a six branched wheel-legged robot

5 结论

本文开展了六支链轮腿式月面机器人构型及机构参数化优化设计，参数化设计及仿真表明轮腿机构尺寸参数及关节角参数对机器人影响明显，在机器人的设计与控制中应重点关注或动态调整；通过参数化优化设计的方法，优化计算得出了较优的机构尺寸及关节角参数，结论及方法可以用于指导工程产品设计。