条形锚板抗拔承载力的离散元分析

洪 丰，徐 彬

（1.中交第三航务工程勘察设计院有限公司，上海 200030；2.中交第一航务工程勘察设计院有限公司，天津 300222）

引 言

系泊系统基础的型式很多，条形锚板基础作为最简单、应用最广泛的基础型式，系统地研究其在海床土中的拔出行为，有助于合理判断锚板的承载性能，为锚板的安装提供技术指导，具有重要的理论和工程应用价值。

海床中锚板的承载力已广泛的研究。理论方面，Balla[1]在平面应力假定和模型试验的基础上提出了一套系统的理论分析方法，同时给出的承载力计算公式。Meyerhof和Adan[2]根据砂土地基中的模型试验提出了锚板极限承载力的经验公式。Merifield等[3]随后运用极限分析法通过增加上部压力分析其影响，并用有限元公式量化了埋深、上部压力、锚的粗糙度对圆形、条形、方形锚的影响。

数值研究方面，Hu和Randolph[4]运用小变形的网格和插值技术（RITSS）模拟了锚的连续拔出问题，并描述了这种方法的具体发展。Merifield[5]采用塑性理论有限元极限分析法，计算了不同埋深和不同内摩擦角下的锚板极限承载力。刘君和吴利玲[6]采用插值技术（RITSS）和小变形网格的有限元法分析了正常固结粘土中锚板的承载力，模拟了锚板的大位移过程。Song等[7]在2D-RITSS方法的基础上将大变形有限元技术运用到圆形和条形锚中。

目前关于锚板承载力的研究，多采用有限元分析方法。这些方法能够很好地计算出锚板的承载力，但土体本质上属于散粒体介质，颗粒流的离散元方法可更好地揭示锚板上拔过程中周围土体的细观特征及承载力特性。本文采用离散元分析技术-颗粒流（PFC2d）建立能够模拟锚板上拔过程的颗粒流模型，详细考察了颗粒刚度、模型粒径比、颗粒摩擦系数、模型孔隙率等细观参数对荷载-位移曲线以及锚板抗拔承载力的影响。通过数值模拟与试验结果的对比分析，验证了该模拟方法的合理性与可行性。

1 模型的建立

1.1 土体的模拟

在颗粒流（PFC2d）模拟中，颗粒之间的接触形式多采用线性接触，本文选用线性接触建立土体模型。模型建立需确定五个细观参数：切向刚度值Ks、法向刚度值Kn、孔隙率n、粒径比rmin/rmax、颗粒与颗粒的滑动摩擦系数μ。在颗粒流模拟中，颗粒是在指定区域内，半径在设定最小和最大粒径范围内随机生成分布，且当模型尺寸和颗粒孔隙率确定时，土体模型便可确定。例如：为建立一个孔隙比n，总面积为A的土体模型，可计算出颗粒总面积Ap=A(1-n)，若颗粒为随机平均分布，则模型中颗粒平均半径为= (rmax+rmin)/2，则模型中颗粒数目

建立土体模型的过程如下：首先生成4个位置固定的墙体单元，在墙体单元确定的区域内生成颗粒，若颗粒比预定值小，可通过颗粒半径扩张法达到预期效果。通过PFC内置语言编程实现模型的建立，主要算法为半径扩张法，其基本思路如下：

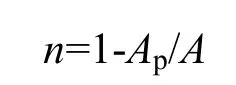
其中：

n为孔隙率；

Ap为颗粒的总体积；

A为模型总体积（假定为单位厚度）。

因此：

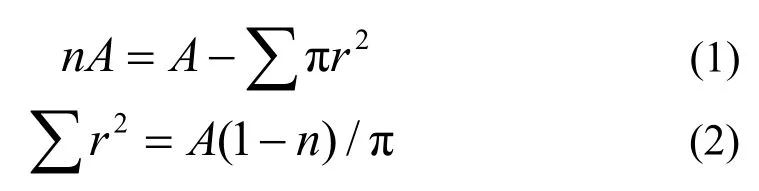
若初始孔隙率为n0，最终孔隙率为n，则：

将所有颗粒都乘以颗粒半径放大系数m，那么有r=mr0，即：

当已知n时，可以预估一个m值，由式（4）反推得到初始孔隙比n0：

当颗粒数目为N时，颗粒的平均半径为：

设最大与最小颗粒半径之比为m，则

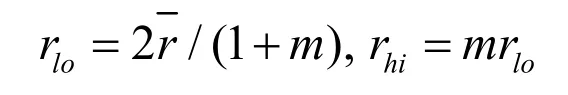
为使颗粒模型在较短时间内达到平衡，即平均接触力和平均不平衡力达到稳定值，可在求解前设置颗粒间的摩擦系数，用于消散颗粒能量，但这种方式干预了颗粒的自由运动，对其最终组合状态有一定影响，因此，需平衡计算时间和颗粒组合状态，选择合适的建模方式。此外，也可以通过软件内置的测量圆方法来观察颗粒局部参数，判断颗粒是否达到平衡状态。

1.2 锚板拔出过程的模拟

锚板由标准墙体单元来模拟，颗粒流PFC中标准墙体单元由任意数目的点连成的线段组成，墙体单元分为有效面与无效面，墙体单元与球体单元的接触只发生在有效面，有效面通过组成墙体单元的点的连接顺序决定，即沿连接方向的左手边为有效面（如图 1）。因而，建立墙体单元时候应运用左手法则，使得墙体单元的有效面与颗粒接触。

图1 标准墙体单元的有效面的划分

2 细观参数的确定

颗粒流PFC数值分析中，可通过设置墙体单元的移动速度和时间来拟合锚板在土体中的位移；墙体单元移动过程中与颗粒发生接触，通过编写内置程序统计墙体在拔出方向所受的合力，以拟合锚板所受的荷载，并将荷载的峰值作为承载力值。

数值分析中的细观参数与试样本身的宏观系数存在很大差异，细观参数的微小变化可能引起宏观结果的重大变化。为确保建立的模型与期望的宏观物理力学行为对应起来，则需要将模型的宏观行为、响应等和与之相关的细观结构力学参数联系起来。本节讨论了颗粒的切向刚度Ks、法向刚度Kn、孔隙率n、摩擦系数μ、粒径比rmax/rmin等微观参数对宏观结果的影响，从而方便模型建立。

2.1 颗粒刚度Kn、Ks对结果的影响

颗粒流PFC数值分析中，通过接触模型来拟合材料的本构特性，本文颗粒间的接触采用刚度模型和滑动模型，刚度模型主要为接触力与相对位移间的弹性关系，即：

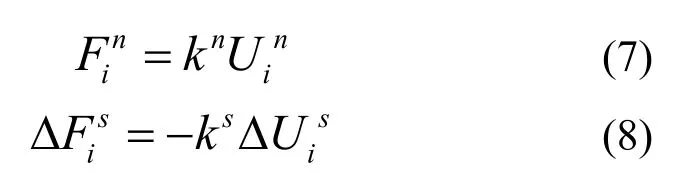
通过两个接触实体（球与墙体或球与球）的切向和法向刚度（Kn、Ks）来定义刚度模型，接触刚度计算式如下：

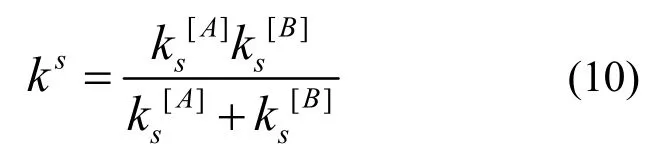
式中[A][B]表示两个接触的实体。

只改变切向刚度Ks，保持模型中法向刚度Kn及其它参数不变，得到切向刚度Ks对结果的影响：图2为不同切向刚度Ks对应的荷载-位移曲线，图3为不同切向刚度对应的承载力曲线，图4为刚度比对应的承载力曲线。从图中可以看出，法向刚度Kn一定时，切向刚度对荷载-位移曲线的影响结果无明显规律，而刚度比(Kn/Ks)接近1时，承载力达到最大。

图2 不同切向刚度Ks的荷载-位移曲线

图3 不同切向刚度Ks的承载力曲线

图4 不同Kn/Ks的承载力曲线

保持模型中切向刚度Ks及其它参数不变，只改变法向刚度Kn，得出法向刚度Kn对结果的影响：从图5、图6中可以看出，切向刚度Ks一定时，法向刚度对荷载-位移曲线的影响结果较为明显，随着Kn增大，曲线也相应增大，即相同位移对应的力更大，而后期都趋于稳定；可初步确定，承载力随Kn的增大而增大，近似为线性正相关关系。

图5 不同法向刚度Kn的荷载-位移曲线

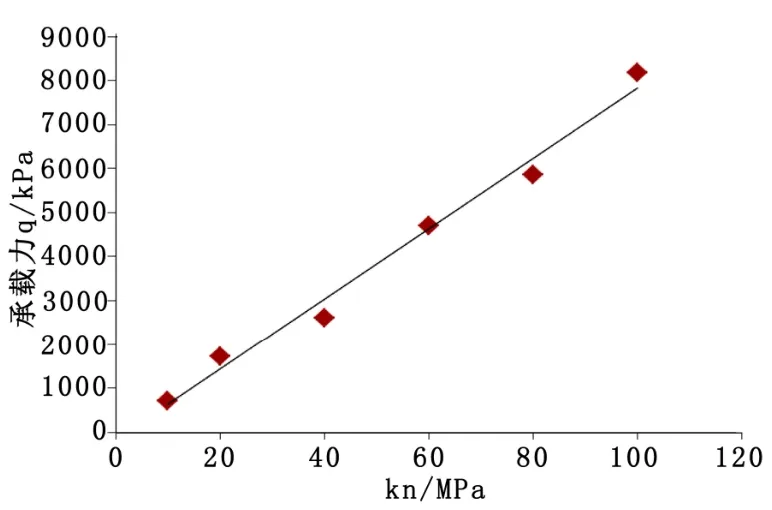
图6 不同法向刚度Kn的承载力曲线

2.2 摩擦系数μ对结果影响

颗粒流PFC数值分析中，接触的滑动模型主要强调切向和法向接触力，两个接触体可以发生相对滑动，通过接触摩擦系数μ来定义滑动模型，通过最大允许切向力来判断是否发生滑动，即：

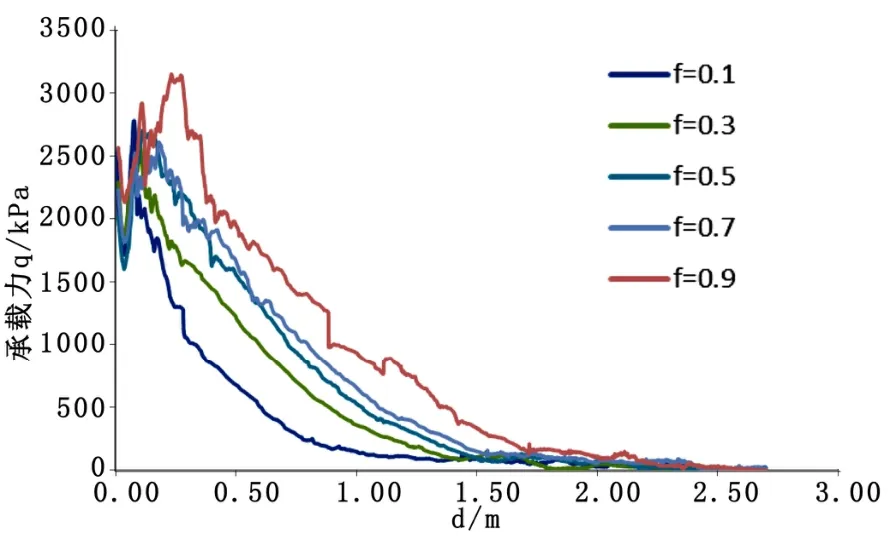
图7 不同摩擦系数μ对应的荷载-位移曲线

图8 不同摩擦系数μ对应的承载力曲线

2.3 模型孔隙率n对结果的影响

模型孔隙率n为建立该模型的一个重要参数，孔隙率n能控制建立模型所产生的颗粒单元的数目，同一模型尺寸下，孔隙率不同，颗粒单元分布密集程度不同。

保持模型中其它参数不变，只改变模型孔隙率n，可得出模型孔隙率n对结果的影响：图9为不同模型孔隙率n对应的荷载-位移曲线，图10为不同模型孔隙率n对应的承载力曲线。可初步确定，模型孔隙率n越大，荷载—位移曲线相同的位移对应的承载力越小；孔隙率n与承载力呈线性负相关关系，即孔隙率n增大，承载力减少。

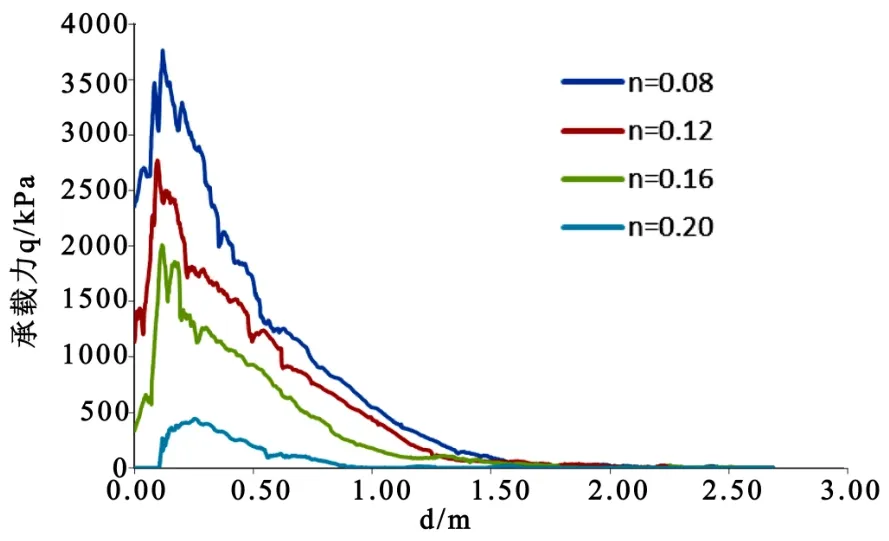
图9 不同模型孔隙率n的荷载-位移曲线

图10 不同模型孔隙率n的承载力曲线

2.4 模型的粒径比对结果的影响

模型粒径比rmin/rmax为建立该模型的另一个重要参数，能够控制建立模型所产生的颗粒单元的粒径分布状况，粒径比rmin/rmax越大，则模型中颗粒单元的半径就越接近，同时，粒径比也能间接控制颗粒数目。

保持模型中其它参数不变，只改变模型粒径比rmin/rmax，得出粒径比对结果的影响：图11为不同模型粒径比rmin/rmax对应的荷载-位移曲线，图 12为不同模型粒径比rmin/rmax对应的承载力曲线。可初步确定，模型粒径比rmin/rmax对荷载—位移曲线有一定影响，粒径比rmin/rmax越小，曲线达到承载力越快；粒径比对承载力影响不明显。

图11 同一模型不同粒径比的承载力曲线

图12 同一模型不同粒径比的承载力曲线

2.5 细观参数标定

通过颗粒模型细观参数对结果影响的初步分析后，进行细观参数的初步确定（表 1），继而进一步建立数值模型并与试验结果进行对比。

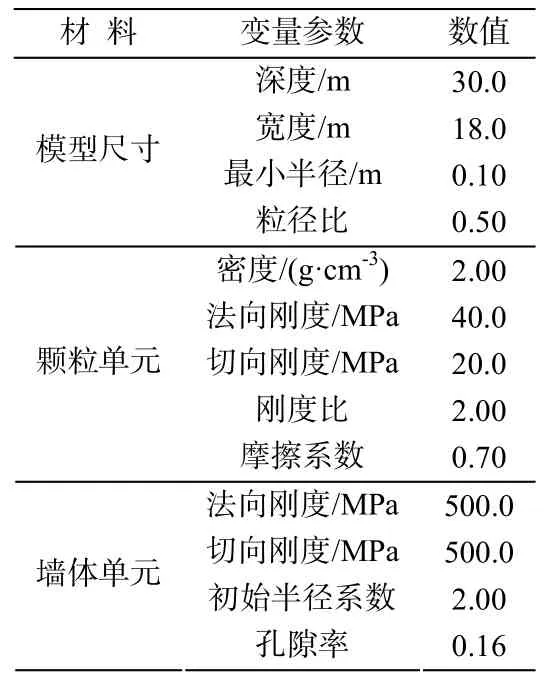
表1 模型的细观参数

3 数值模拟

3.1 数值模拟步骤

颗粒流PFC数值模型初步建立步骤如下：

1）在尺寸为18 m×30 m的空间内，随机生成指定粒径范围的圆形颗粒，并删除该空间外的颗粒；

2）施加重力，进行平衡迭代计算，使颗粒自由运动，直至稳定状态；

3）编制程序删除锚板位置的颗粒，然后生成墙体单元模拟锚板（板宽B=3 m，埋深h=2B和h=5B）；

4）再次平衡迭代，直至平均不平衡力与平均不接触力的比值小于0.1 %，此时颗粒流PFC数值模型初步建成。

通过上述4步生成数值模型如图13所示。

图13 数值试样模型示意

对墙体单元施加竖向速度及运动时间来模拟锚板上拔过程；最后通过参数的调节，将数值结果与试验结果进行对比，使数值结果接近试验结果，从而得到一组恰当的细观参数，进而利用这些参数进行其他加载条件下数值模拟。

3.2 数值模拟结果分析

锚板基础荷载-位移关系曲线数值结果如图14，曲线可大致分为三个阶段：第一阶段为荷载迅速上升段（峰值为承载力）、第二阶段为下降段（承载力后明显地下降）、第三阶段为稳定段（荷载趋于稳定）。

图14 锚板基础荷载-位移关系曲线数值结果

由砂土地基中锚板基础抗拔性能的模型试验[8]荷载-位移曲线可知（图15），锚板荷载-位移关系曲线可分为三个阶段：承载力迅速上升段、剪胀软化段、残余稳定段。数值模型的结果与该试验结果具有相同的趋势，由此可以初步说明颗粒流PFC用于模拟锚板拔出过程是可行的。

图15 锚板基础荷载-位移关系曲线试验结果

4 结 论

本文系统考察了颗粒刚度Kn、Ks，摩擦系数μ，模型孔隙率n，粒径比rmin/rmax等细观参数对荷载-位移曲线和锚板承载力的影响，确定了该模型下的细观参数，给出了数值模拟步骤，并进行相关的数值计算。得到了以下结论：

1）数值计算结果表明法向刚度Kn与承载力值近似为线性正相关关系；切向刚度Ks对承载力值影响不明显，刚度比Kn/Ks接近与1时，承载力值达到最大；摩擦系数μ对承载力值的影响不明显；模型孔隙率n与承载力呈线性负相关关系；粒径比rmin/rmax对承载力值影响不明显。

2）将数值模拟与试验结果的对比表明：颗粒流 PFC可以模拟出的砂土地基中锚板荷载-位移曲线的三个阶段：上升段、下降段、稳定段。这与试验结果的发展阶段吻合，证明了颗粒流PFC用于模拟锚板拔出过程的可行的。