现役地下结构容许位移值在盾构开挖沉降量控制中的应用

赵海亮，李 军

（济南市市政工程设计研究院（集团）有限责任公司，山东 济南 250101）

0 引言

随着我国综合实力的提升，城市地下综合管廊工程和城市轨道交通工程得到快速发展，建设过程中两者交叉施工的工况经常出现。尤其是两者结构距离较近的情况下，既要保证综合管廊结构安全，又能保障管廊内管线正常运营显得尤为重要。本文结合某地工程实例，对采用盾构技术开挖的轨道交通下穿已有综合管廊的工况进行分析，提出基于地下结构正常使用状态下地基沉降控制方法。该方法从保障结构安全及正常运营情况下所能允许的最大沉降值为基础，对盾构开挖过程中沉降量的控制提出要求。

1 现有基本理论

1.1 盾构开挖影响范围—Peck公式及相关修正公式[1,4-8]

盾构开挖过程中原有力学平衡被打破，发生应力重分布，围岩向开挖区域产生位移，对此国内外学者根据施工经验，总结出多种地基沉降预测公式。一般情况下，单线开挖的盾构，其开挖影响范围及最大沉降量一般采用Peck公式及其相关的修正公式；而双线开挖，一般采用叠加法进行计算。Peck认为：地表沉降槽的形状与正态分布相似；横向地表沉降槽形状见图1。

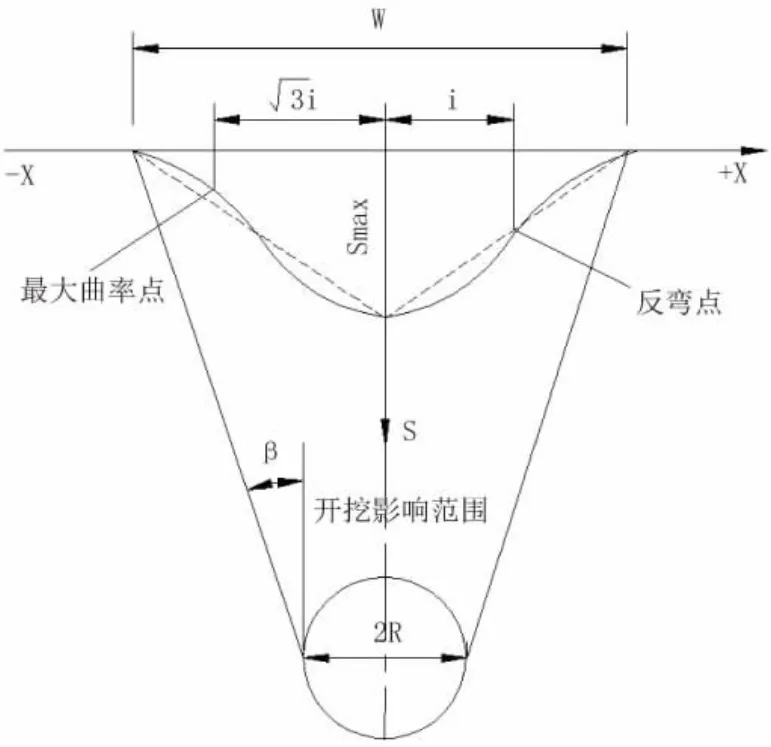
图1 横向地表沉降槽

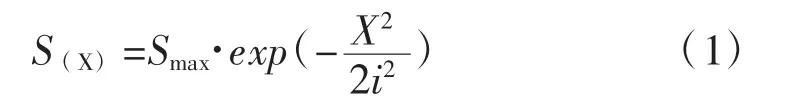
横向地面沉降经验公式为：

式中：S（X）为地面沉降量；x为以隧道中心线位置为原点的地面水平坐标系；Vloss为隧道单位长度的土体损失率；i为地表沉降槽宽度系数；η为土体损失率；R为盾构半径；w为沉降槽宽度；h为盾构覆土厚度。

1.2 地下结构与土相互作用--弹性地基理论[1,3]

弹性地基按照Winkler假定，任意一点的土的抗力与该点的位移成正比求解；假设土体是土弹簧。该假定基本概念明确，方法简单，所得结果一般较安全，在国内外工程界得到广泛应用。

2 基于地下结构正常使用状态下地基沉降控制方法

本文中的方法以地下结构强度、刚度的最大容许值和其内部管线正常使用时所需的条件作为控制条件，反推在满足上述要求下结构位移值，将该位移值作为盾构开挖过程中的控制目标。

2.1 以地下结构强度和刚度容许值为控制条件

首先结合工程实际情况，由Peck公式及相关修正公式[1,4-8]确定盾构开挖影响范围，该工程影响范围见图2。

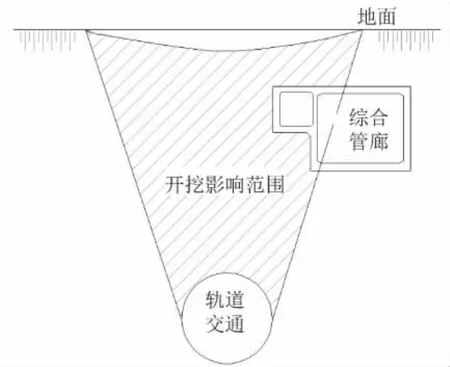
图2 盾构开挖影响范围示意图

盾构开挖后，由于处于盾构开挖影响范围内综合管廊底板下土体产生损失，其下部土体提供的反力减小，从而产生附加荷载。又因管廊结构刚度比较大，结构本身会对附加荷载产生抵抗弯矩，另外管廊与土体之间具有复杂变形协调，最终达到受力平衡[1]。故可以将此时管廊的受力模型简化为如图3所示两种。

图3 管廊边界条件

简化模型1是将位于盾构开挖影响范围外的结构与土体之间相互作用，采用“m法”确定地基土比例系数，面弹性支撑模拟；盾构开挖影响范围内的结构与土体之间相互作用，通过调整面均布荷载n×f1（f1为单位力）的数值来模拟。简化模型1计算公式如下：

简化模型2是将结构与土体之间的相互作用，采用“m法”确定地基土比例系数，面弹性支撑模拟；盾构开挖影响范围内管廊因下方土体损失引起的附加荷载，通过调整面均布荷载n×f1（f1为单位力）的数值来实现附加荷载的影响。简化模型2计算公式如下：

式中：[M]为控制截面结构最大抗力；M为外荷载（除附加荷载nf1）作用下最大内力；n×M1为n×f1附加荷载作用下最大内力。

具体思路：主体结构在上述简化模型情况下，控制截面所能提供的最大抗力[M]作为限值，求解系数n。

根据求解得到的系数n，确定对应系数n状态下结构位移值，该位移即为以地下结构强度和刚度容许值为控制条件下，盾构开挖过程中结构允许变形值。

2.2 结构内部管线正常使用时所需条件作为控制条件[7-10]

如图4所示，盾构开挖影响范围内管廊节段沉降量要大于其相邻节段，管廊节段内管线及相应附属设施能否满足规范要求并正常使用，需要进行评价。故可以通过综合考虑管廊内管线、管线接头、管线挠度、支架等在满足正常使用时所允许的管廊节段最大沉降值，进而对盾构开挖过程中沉降量提出控制条件。

3 数值分析

本数值分析模型以某实际工程为背景，项目中盾构下穿已有综合管廊，并且盾构与综合管廊距离比较近，对沉降值的控制要求非常高；本数值分析主要从地下结构强度、刚度的最大容许值出发，分别对简化模型1和简化模型2进行数值分析，对计算结果进行对比，对盾构施工过程中影响范围内土体沉降值提出控制要求。

图5为计算模型，用Midas civil 2017板单元建模，其边界条件模式见图3，地基基床系数20 000 kN/m3。

图5 计算模型

板单元内力见图6，经数值分析发现，在盾构开挖影响边界处，管廊底板内力值最大。根据控制截面的截面特性，结构所提供最大抗力[M]=218 kN·m。经简化模型1确定的参数n的取值为82.8，此时对应结构位移最大允许位移值为6.4 mm；经简化模型2确定的参数n的取值为21.9，此时对应结构位移最大允许位移值为5.7 mm。简化模型计算结果见图7。

图6 板单元内力图

4 结论

（1）本文提出以管廊结构强度刚度的最大容许值为限值，确定在此限值下结构容许位移值，以此作为盾构开挖过程中沉降量控制条件。

（2）文中提出以管廊内管线、管线接头、管线挠度、支架等在满足正常使用时所允许的最大沉降值为控制条件，以此作为盾构开挖过程中沉降量控制条件。

（3）数值分析结果表明，在盾构开挖影响边界处，结构底板内力值最大；对比数值分析结果发现，简化模型1和简化模型2计算结果基本一致。

（4）本文对边界条件的简化仍需进一步优化，首先结构与土的相互作用采用“m法”确定地基土比例系数，而对地基土比例系数取值方法不同，其计算结果也有差异；其次，通过施加n倍单位面均布荷载来模拟沉降的影响，而不均匀沉降范围内实际受力情况并非均布荷载。后续可在上述基础上做深入研究。