基坑三维弹性地基梁法中m值的确定方法

赵香山

（上海市政工程设计研究总院（集团）有限公司，上海市 200092）

0 引言

近几年城市综合管廊的兴起、地下空间的利用和高层建筑的兴起带来了大量的基坑工程，其中也发生了不少工程事故，造成巨大的经济损失和不良的社会影响。除了经济、管理等方面的因素，技术方面的因素在很大程度上是因为对土体性质认识不足。为了控制环境影响和工程风险，必须合理准确地预测和评估基坑工程的变形特征和大小。数值分析是一种有效的方法，并且已经在基坑工程中得到大量应用[1]。围护结构的强度和变形计算是基坑工程设计的关键技术，m法是基坑工程中把挡墙作为弹性梁单元，用土弹簧模拟坑内被动土压力的竖向平面弹性地基梁法。m法以其计算参数少、模型简单、能模拟分布开挖、能反映被动区土压力与位移的关系等优点而广泛地应用于基坑开挖围护结构受力计算分析中。然后m法受其本身为平面分析方法的局限，在应用于具有明显的空间效应的深基坑工程时不得不进行较大简化，且不能反映实际支护结构的空间特征。采用了可以考虑土与支护结构空间共同作用的简化有限元计算方法——三维弹性地基梁法，该方法基于弹性地基梁法中的m法原理，将其从平面拓展到空间，m值的确定是三维弹性地基梁法数值模拟的关键和难题。

反分析方法的出现为解决这个难题带来了非常优秀的手段。1971年Kavanagh等[2]首先通过有限元方法反分析弹性模量。1980年Gioda等[3]将该方法应用于岩土工程中反算黏聚力和内摩擦角。近年来更是研究多种算法和案例，Hashash等[4-5]提出了SelfSim方法用于分析基坑土体变形。Zhang等[6-7]采用MCMC反分析边坡稳定的可靠性。国内学者也纷纷对此进行研究，李镜培等[8]分析了径向基神经网络并将其用于实际工程中来预测基坑支护结构的水平位移。郑俊杰等[9-10]提出了计算岩土工程可靠度指标和设计验算点的全局优化算法，并讨论了β分布在岩土工程模糊可靠性分析中的应用。张俊峰等[11]以基坑旁的隧道变形为目标反分析基坑开挖的土体弹性模量，引入了权函数来保证反分析出的土体参数同时满足隧道的隆起变形和连续墙的水平位移。但是现有方法通常以单一实测数据为基础确定土体参数，难以反映基坑等地下结构的综合特征。

针对以上现状，采用ABAQUS对上海轨道交通13号线长寿路车站基坑进行有限元模拟，关联AMALGAM算法，选取长寿路车站基坑的长边和短边各一个连续墙侧移作为两个目标，利用MATLAB对基坑进行多目标反分析，得到了可以用于数值模拟长寿路车站基坑的m值，并对多目标反分析结果对后续步施工对环境的影响的预测效果进行了评估。

1 工程实例及数值分析模型

上海轨道交通13号线长寿路站为7号线与13号线的L形换乘站，选定的监测点CX3位于标准段12轴，采用800 mm厚、39 m深的连续墙（8 m素混凝土）；沿基坑深度方向设置五道支撑；其中第一道为钢筋混凝土支撑，其余均为ø609钢支撑。

根据地勘资料，基坑周围土体分为六层，其中第一层为1.7 m厚的①杂填土，第二层为1.6 m厚的②1褐黄至灰黄色粉质黏土，第三层为2.9 m厚的③2灰色砂质粉土夹粉质黏土，第四层为7.8 m厚的④1灰色淤泥质黏土，第五层为10.2 m厚的⑤1-1灰色黏土，第六层为4.2 m厚的⑥暗绿至草黄色黏土，第七层为7 m厚的⑦1草黄至灰黄色砂质粉土，第八层为6.1 m厚的⑦2灰黄至灰色粉土，第九层为28.5 m厚的⑧灰色黏土。

整个施工过程如下：

第一步，添加第一道支撑，并开挖至6.2 m；第二步，添加第二道支撑，并开挖至9.1 m；第三步，添加第三道支撑，并开挖至12.1 m；第四步，添加第四道支撑，并开挖至15.1 m；第五步，添加第五道支撑，并开挖至17.0 m；第六步，添加底板。

2 计算原理及模型建立

2.1 空间m法计算原理

竖向弹性地基梁法是基坑工程中用于计算板式围护体系围护墙的内力和变形的计算算法。计算时需要考虑基坑施工过程中多方面因素的影响，如支撑点的位移、施工工况、支撑刚度及周围基底深坑等对围护结构的影响。

竖向弹性地基梁做了如下假定：坑外土体以侧向压力形式表现，其分布形式通常取地表处为0，至开挖面附近为三角形分布，其下土层可以照矩形分布，也可按照工程经验分布。坑内开挖面以上内支撑和开挖面以下土体以弹性支座模拟，如图1所示。

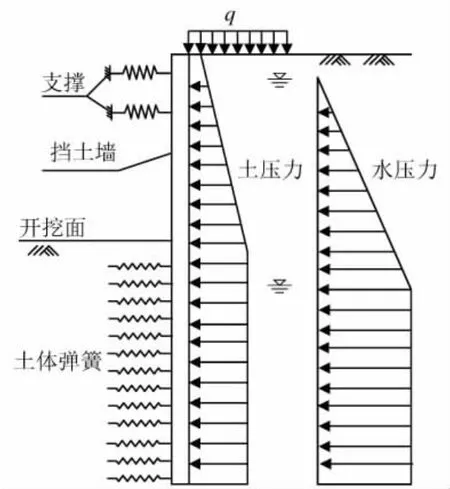
图1 弹性地基梁法示意图

基坑支护结构的三维分析模型如图2所示。

图2 基坑支护结构的三维分析模型

其中，内支撑如对撑、角撑等，压缩弹簧刚度根据支撑体系布置、构件材料等条件按下式计算确定：

式中：KB为支撑弹簧刚度，kN·m/m2；E为支撑弹性模量，kN/m2；A为支撑的截面积，m2；α 为折减系数；l为支撑构件的计算长度，m；S为支撑构件的水平间距，m。α与支撑松弛有关，一般取0.5～1.0；混凝土支撑或钢支撑施加预压力时，取α=1.0。

坑内土体水平向弹簧支座和垂直向弹簧支座的压缩弹簧刚度KH和KV，按下列公式计算：

式中：KH、KV分别为地基土的水平向和垂直向基床系数，kN/m3；m为水平基床系数沿深度增大的比例系数，kN/m4；z为基坑开挖对坑底土体的影响深度；b、h分别为土体弹簧的水平向和垂直向计算间距，m3。

2.2 数值模型

采用ABAQUS对实际方案中的长寿路车站基坑进行三维有限元模拟，围护结构选取S4（四个节点的空间壳单元）进行模拟，板的单元尺寸为1 m×1 m，水平方向的支撑选取三维模型中的梁单元B31进行模拟，开挖面以下设置弹簧单元，如图3所示。

根据监测数据的完整程度，一共对四个工况进行反分析：第二步，添加第二道支撑，并开挖至9.1 m；第三步，添加第三道支撑，并开挖至12.1 m；第四步，添加第四道支撑，并开挖至15.1 m；第五步，添加第五道支撑，并开挖至17.0 m。

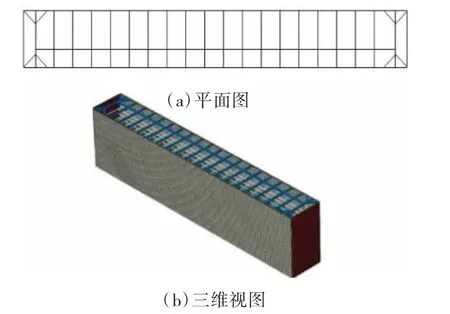
图3 基坑开挖有限元模型

每一步荷载的改变通过ABAQUS中的子程序DLOAD来实现，弹簧刚度的调整通过ABAQUS中的场变量来实现，具体实现方式如下：

在弹簧刚度定义命令中加入如下语句：

*Spring,elset=Springs39-spring,

DEPENDENCIES=1

2;1e7,,,0;1e7,,,1;1e7,,,2;1e7,,,3；1e7,,,4;1e7,,,5

“1e7,,,1”中的“1”代表场变量，同时在每一个step定义结束时添加如下语句，“allnode,1.”中的“1.”对应场变量。从而将弹簧刚度的改变与step关联起来：

*FIELD,VARIABLE=1

allnode,1.

根据上海基坑工程技术规范给出m值的初始值，见表1。

表1 砂土层土体参数

2.3 分析对象

基坑位移变化容易得到，是土体力学性质参数的函数，也是监测的重点。在该案例中，为了更加全面地对土体参数进行分析，同时考虑围护结构长边和短边的变形（墙体侧移）两个因素，采用均方根误差作为目标函数，即

式中：n为测点数目；S*i为第i个测点的实测值；Si为第i个测点的模型计算值。

根据上海基坑工程技术规范，反分析时给定m值范围，见表2。

表2 优化参数上下界

3 参数确定结果分析

3.1 土体参数确定

选取第二步开挖结束的数据进行分析，多目标分析同时考虑测点CX3和测点CX8的墙体变形的影响，经过反分析生成Pareto最优解集，如图4所示。三角是最后一代计算得到的Pareto最优解。由图4a～e可以看出，由于两个目标均为侧移，观察从第一代到第二十代的所有的点时可以发现两个目标都是随着代数的增加而减小的趋势，将最后一代局部放大，将其连接成为Pareto曲线（见图4f），可以看出该曲线有明显拐点。可以认为曲线属于尖锐型，可以获得一个较好的协调最优解。总目标函数权重系数ω1取值对结果有一定的影响。Mertens提出双目标时，取ω1=0.5作为近似最优解，在下面将选取ω1=0.5的反分析参数代入模型进行计算并且讨论。

对两个目标函数进行标定，化为相同量级后作转化Pareto图，如图5所示。三角为转化Pareto最优，大圆为总目标函数取ω1=0.5所得的协调最优点。

3.2 基坑变形预测与比较验证

根据第二步开挖反分析所得ω取0.5时，反分析出的参数代入模型进行正分析的结果与测量结果的比较如图6所示。根据第二步开挖结果确定土体参数之后通过数值模拟分别预测第三至第五步开挖引起的响应，同时与测量结果做比较以验证，由第二步开挖的监测数据确定的m值代入模型进行正分析的预测结果与实际数据的对比如图7所示。由对比结果可以看出，由第二步开挖结果的CX3和CX8测点的连续墙侧移作为目标对m值进行确定之后代入模型进行正分析的结果与实际监测结果的一致程度相当高，误差的出现主要是因为在开挖面以上的部分结构自身的刚度和支撑的刚度都已经确定，这是由于m值确定过程中只能调整开挖面以下的m值，因此对开挖面以上墙体侧移的调整效果不大。确定的m值代入进行正分析的结果与第三至第五步开挖结果的实际监测数据也比较一致。可以认为，由第二步现场监测结果确定的土层参数代入有限元模型能够很好地模拟实际的开挖过程。

图4 CX3和CX8墙体变形多目标分析Pareto图

图5 转换后的CX3和CX8墙体变形多目标分析Pareto图

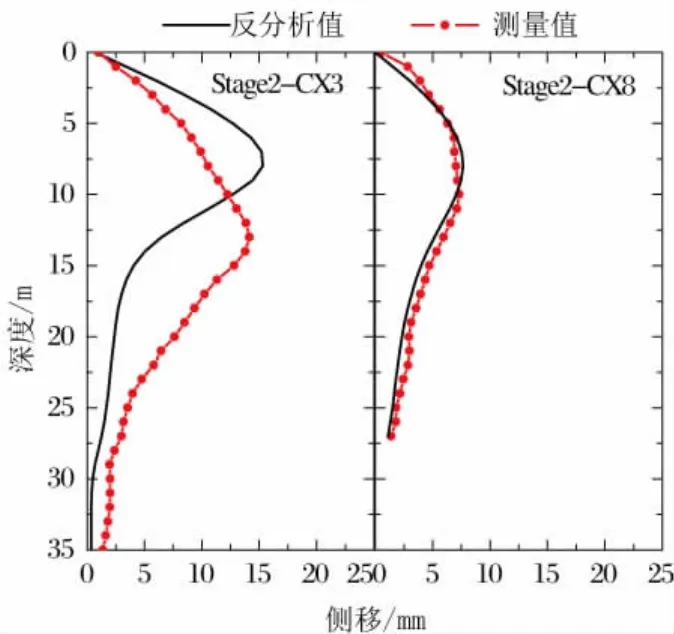
图6 ω不同取值时的正分析结果比较图

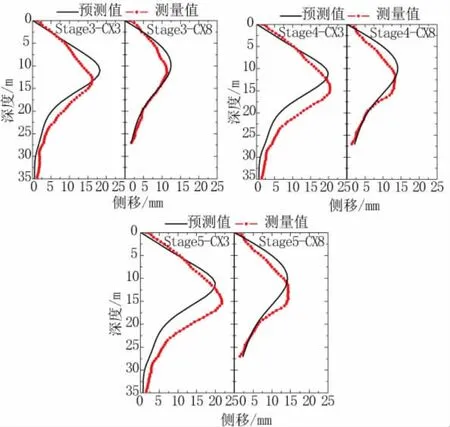
图7 第二步反分析结果地表沉降预测与实测值对比图

根据每一步开挖的实测结果反分析出的m值见表3。可以发现，反分析出的土层参数与输入的初始值有明显的不同，反分析出的第四层土体的m值较大，逼近所给的m值上限，第五至第八层土体反分析出的m值逼近所给范围的下限。

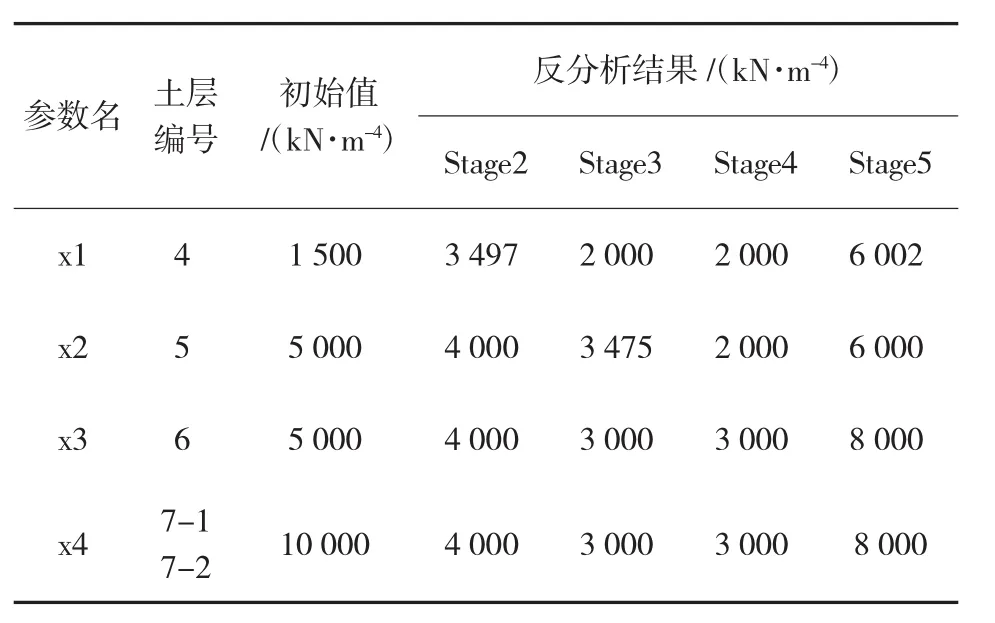
表3 砂土层土体参数

4 结语

（1）三维弹性地基梁法不仅继承了常规情况下的基坑支护结构分析的思路，有原理较简化、计算参数较少、概念明确等优点，又避免了传统的竖向弹性地基梁法过于简化从而导致不能考虑支护结构空间效应的缺点。

（2）由于经验的m值代入三维弹性地基梁模型的计算结果与实测结果有一定差距，提出了多目标反分析法得到能够较为合理的模拟基坑开挖过程的m值。

（3）三维弹性地基梁法能在一定程度上反映出围护结构在基坑开挖过程中的空间效应，但是由于在实际基坑开挖过程中的工况较为复杂、开挖及支撑支护不及时、土体流变等种种因素的影响，导致计算结果与实际施工工况依旧有一定程度的差异。因此如何用三维弹性地基梁法考虑比较复杂的工况还有待进一步的讨论。