基于半解析砰击模型的弹性楔形体入水冲击分析
于鹏垚, 赵 勇, 王天霖, 甄春博, 苏绍娟
(大连海事大学 船舶与海洋工程学院, 辽宁 大连 116026)
船舶砰击载荷与结构响应在船舶与海洋工程领域具有重要的研究意义.高频的砰击载荷可能会引起结构的塑性变形和疲劳损伤,而且伴随着轻质复合材料的应用,冲击过程中的结构变形与流场间的耦合作用也愈发突出.V形剖面是高速船舶的典型剖面形式,因此,在砰击问题研究中,楔形体入水冲击模型被广泛地采用.
Faltinsen[1]结合正交板理论和Wagner解析砰击模型[2]分析了双体船湿甲板的砰击响应,其中,冲击速度考虑了湿甲板弹性变形的影响.Khabakhpasheva等[3]基于Wagner理论和梁理论求解二维楔形体的入水冲击响应,并给出3种近似求解方法,讨论了不同耦合程度下各方法的求解精度.采用不同的结构响应求解方法,Shams等[4]和Datta等[5]也利用解析Wagner砰击理论分析了楔形体的入水冲击响应.陈震等[6]利用Dytran软件对二维楔形体的入水砰击问题进行仿真分析.Stenius等[7]利用LS-DYNA软件分析了二维弹性楔形体入水冲击的流固耦合机理,曹正林等[8]也采用类似方法进行三体船砰击载荷的分析.Piro等[9]采用CFD软件Openfoam求解流场,采用模态叠加法求解结构响应,进而分析了二维弹性楔形体入水和出水过程的振动响应.莫立新等[10]开展了不同刚度楔形体的入水砰击试验.王文华等[11]采用一种新型的CFD方法分析了各状态参数对弹性楔形体入水性能的影响.
按照流场的求解方法不同,弹性楔形体入水冲击的流固耦合分析方法可分为基于解析砰击模型的分析方法和基于计算流体力学的分析方法,与基于计算流体力学的分析方法相比,基于解析砰击模型的分析方法计算效率更高[12].现有的基于解析砰击模型的分析方法普遍是基于Wagner模型进行流场求解,Wagner模型仅考虑了砰击压力的一阶线性项,而且未考虑流动分离后的水动力.本文基于半解析砰击模型[13-15](引入虚拟物面的 Modified Logvinovich Model[12],MLM)建立弹性楔形体入水冲击响应的流固耦合分析方法,其中,流场的求解是在MLM的基础上实现的,结构响应采用模态叠加法来计算,并计入结构弹性振动对冲击速度的影响来实现耦合作用的分析.与基于Wagner模型的水弹性分析方法相比,该方法不仅计及砰击压力的二阶项,而且能够实现流动分离后楔形体动力响应的分析.
1 半解析砰击模型
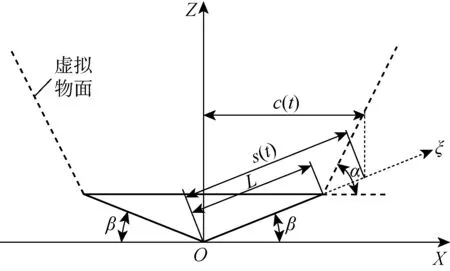
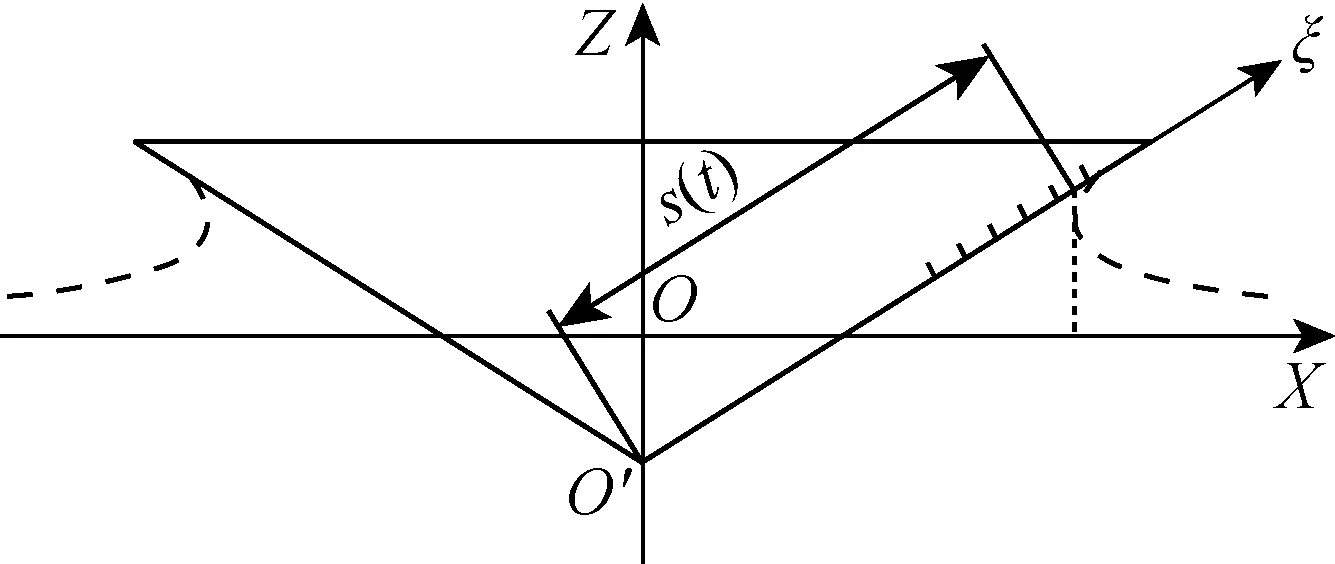
如图1所示,初始时刻t=0,流体静止,OX轴与初始静水面重合,楔形体为对称剖面,其与静水面的交点位于XOZ平面的原点O处.O′ξ轴沿着楔形体的斜边方向,初始时刻,O′与原点O重合.n为楔形体斜边的法向方向,远离流体的方向为正.c(t)为水平方向的浸湿半宽,s(t)为沿着斜边的浸湿长度.假定流体为不可压缩的理想流体且忽略重力的影响,利用伯努利方程并考虑速度势空间导数对应的二阶项,可得流场内任意一点的压力
(1)
式中:ρ为流体的密度;φ(x,y,t)为流场内的速度势;φt为速度势的时间导数.

图1 入水砰击的坐标系与参数Fig.1 Coordinates and parameters of water entry
在砰击剖面为钝形剖面的前提下,Korobkin[12]采用渐近分析方法详细地推导了MLM砰击模型,得到匀速入水时,楔形剖面表面压力沿OX轴水平方向的分布为
(2)
式中:V为剖面匀速入水的速度;β为楔形剖面的斜升角.
c(t)可由下式的Wagner条件进行求解:
(3)
对于斜升角为β的楔形剖面,则有
(4)
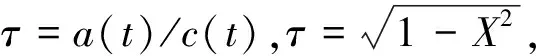
(5)
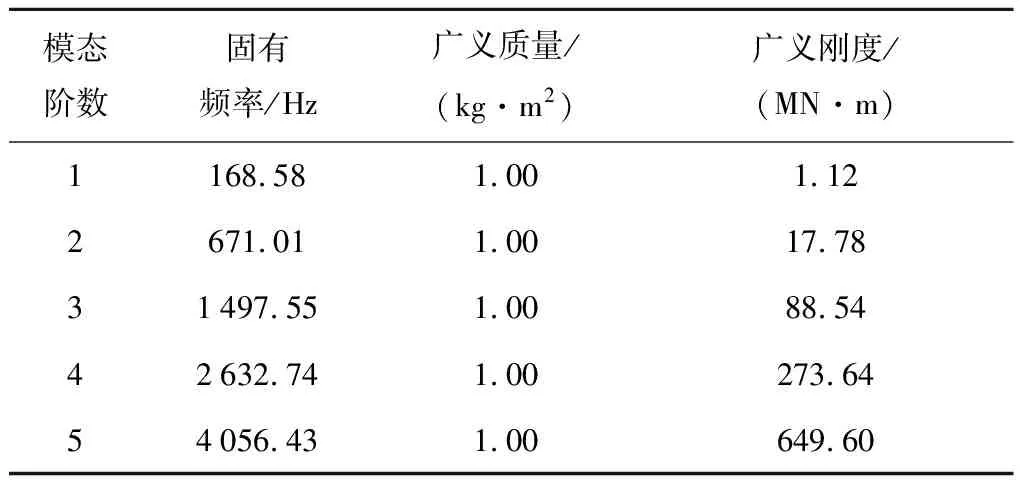
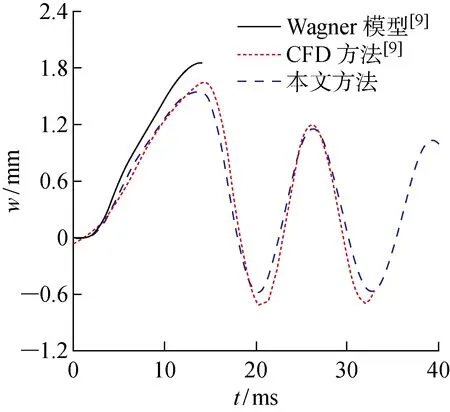
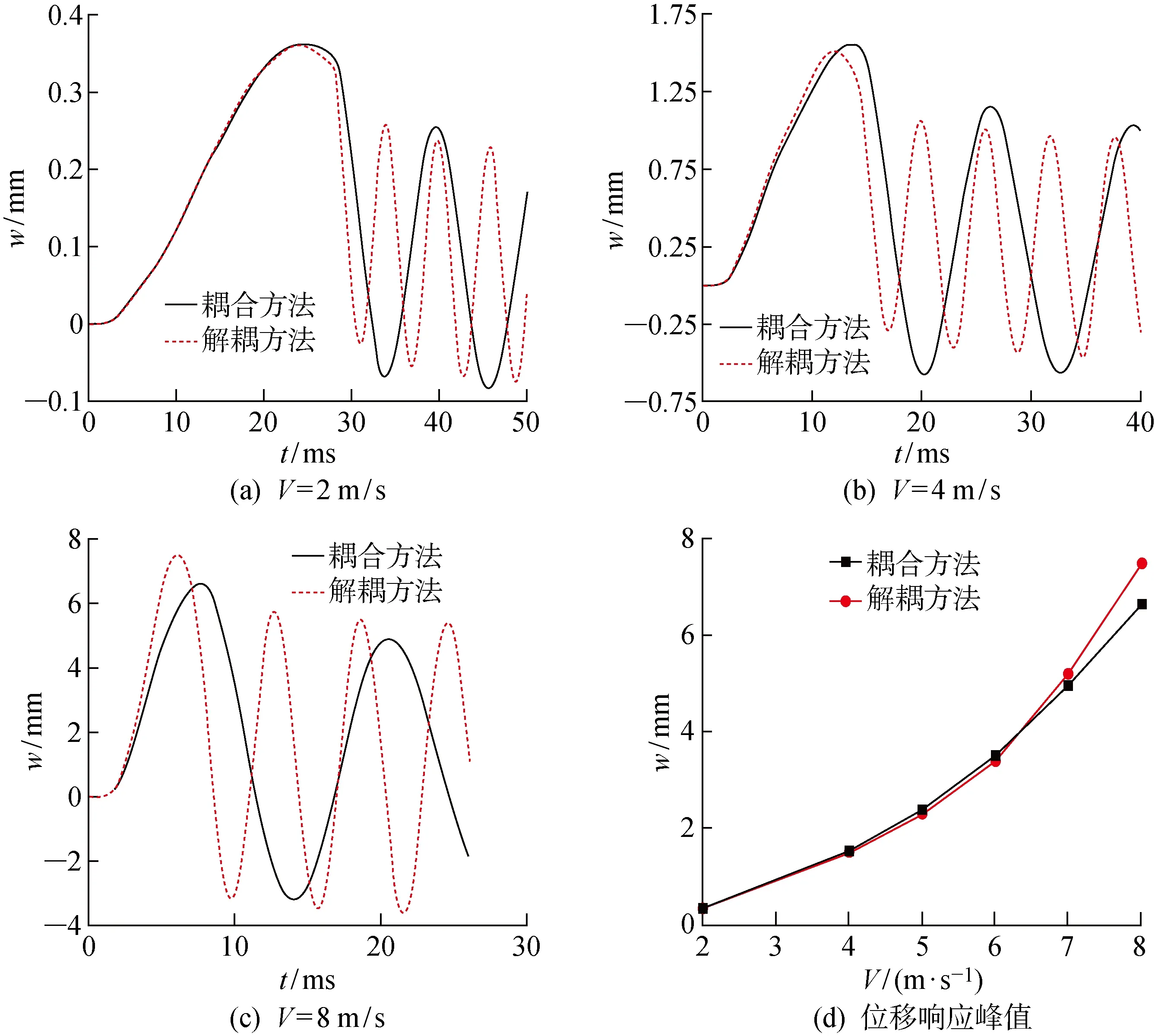
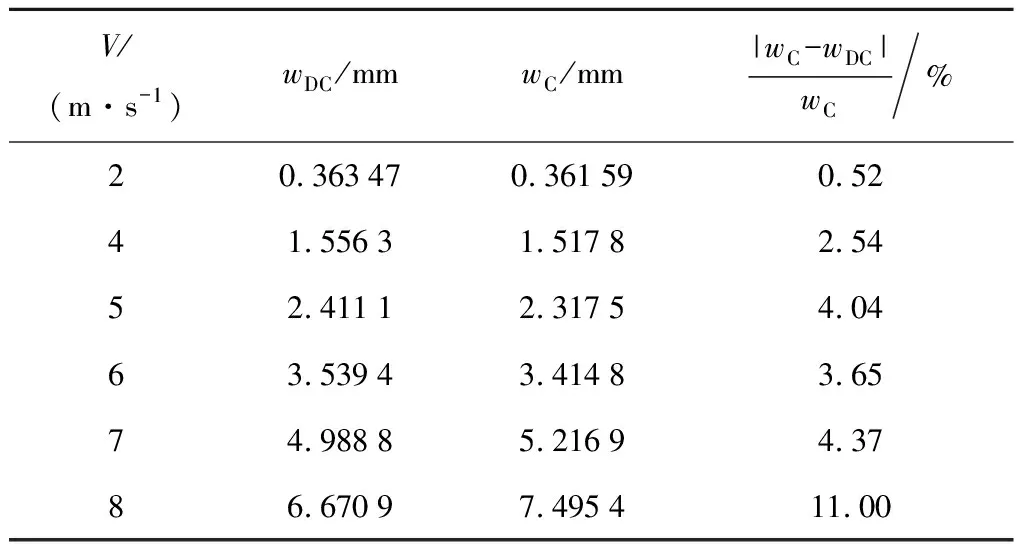
当β已知时,τ即为一个定值.此时利用τ将 -a(t) (6) 可见,当x=c(t)时,P(x,t)=0,避免了不合理的负压. 当楔形剖面为有限宽度时,冲击过程中水流会沿着楔形体的表面发生分离.对于流动分离后的砰击载荷,可以采用引入虚拟物面的方法进行分析[13-15].如图2所示,在流动分离边界处,引入斜升角为α的虚拟物面,假设在流动分离发生后,液面沿虚拟物面上升,对应斜边长度为L的楔形剖面,其剖面形状表达式为 f(x)= (7) 图2 流动分离后的参数Fig.2 Parameters after flow seperation (8) 当发生流动分离后,引入θs,假定当θ=θs时,有c(t)sinθs=Lcosβ,那么 (9) (10) 为便于计算广义力,利用c(t)=s(t)cosβ,x=ξcosβ,可得砰击压力沿O′ξ轴的分布 (11) 相应的楔形体斜边浸湿速度为 (12) 在弹性结构的入水冲击过程中,结构的自身振动会与流场间产生耦合作用,文献[1,7]中的处理方法,是利用楔形体浸湿范围内的平均振动速度来修正刚性楔形体法向n方向的冲击速度,进而得到计及结构弹性效应的压力分布 (13) 同样,考虑弹性振动对冲击速度的影响,可得楔形体斜边浸湿速度 (14) 为便于后续推导,将弹性楔形体周围的压力场分解为刚体冲击对应的压力项Pr(ξ,t)和弹性效应对应的压力项Pe(ξ,t),即P(ξ,t)=Pr(ξ,t)+Pe(ξ,t),则有 (15) (16) 本文采用模态叠加法计算楔形体入水冲击过程中的结构响应,需给出各阶模态对应的广义力.若第i阶振动模态下,沿着斜边法向方向的位移振型为ψi(ξ),则在斜边浸湿长度为s(t)时,对应的广义砰击力为 (17) 令fi(s(t))=fexc,i(s(t))+fela,i(s(t)),则有 (18) (19) 式中:fexc,i(s(t))为楔形体剖面的广义激励力,其仅与剖面的振型和刚性剖面所受的砰击压力有关,而与剖面的弹性振动无关;fela,i(s(t))为弹性效应引起的广义水动力. 若楔形体j阶振动模态对应的主坐标为pj(t),可得湿表面上的瞬时平均振动位移、瞬时平均振动速度和瞬时平均振动加速度的表达式 (20) (21) 将式(16)和(20)代入式(19),弹性效应引起的广义力可以进一步表达为 (22) 式中:Aij(s(t))为楔形体的广义流体附加质量;Bij(s(t))为振动速度线性项对应的广义流体附加阻尼;Dij(s(t))为振动速度平方项对应的广义流体附加阻尼.其表达式应为 ψi(ξ)dξ (23) (24) (25) 那么,在第i阶振动模态下,楔形体剖面对应的广义砰击力为 (26) 在不计及结构阻尼时,基于模态叠加法建立的楔形体动力学方程为 (27) 式中:a为结构广义质量矩阵;c为结构广义刚度矩阵;F为广义力矩阵. 将式(26)代入式(27),可得弹性楔形体入水冲击的流固耦合方程 (28) 式中: m为计入的弹性模态数目. (29) 在具体求解中,本文采用适用范围更广的有限元方法来进行结构模型的模态分析,得到楔形体的离散振型ψi(ξ).对于式 (23)~(25)中的积分值,可借助有限元模型的网格节点通过梯形积分来计算.如图3所示,O′ξ线上的短线代表有限元模型中离散节点的位置,由于楔形剖面上的网格是预先划分,当计算中s(t)从零开始逐渐增大,会存在s(t)的端点恰好位于两节点之间.若计算该时刻广义力,需要重新插值得到s(t)端点位置对应的振型,并求解式(23)~(26)中的积分.而在每个时间步上都进行振型的插值和求积分需要消耗大量时间,也将导致计算更加复杂. 图3 网格与浸湿长度的关系Fig.3 Relationship between mesh and wetted length 为解决上述问题,以第i阶弹性模态为例,预先计算一系列s值下的下列各式的函数值 (30) (31) (32) (33) 式中:sk取值恰好位于有限元模型中的节点处.当t时刻s(t)位于线元的中间时,采用线性插值的方法确定瞬时时刻的上述积分T1,i(s(t))、T2,i(s(t))和T3,i(s(t)),则t时刻Aij(s(t))、Bij(s(t))和fexc,i(s(t))可以分别表达如下 可以看出,利用上述方法更新水弹性方程式(28)中的相应系数,避免了每个时间步上振型的插值和积分的求解,加快了计算速度. 以文献 [9] 中的弹性楔形体为例进行分析,其中,楔形体底升角为10°,斜边长度L=0.5 m,板条梁的厚度h=18 mm,结构材料为钢材,密度为 7 850 kg/m3,弹性模量E=210 GPa,流体的密度为 1 000 kg/m3,板条梁两端取为简支边界.楔形体的冲击速度为4 m/s.本文计算中,楔形体的模态分析利用商业有限元软件Nastran来实现.采用壳单元进行板条梁的建模,建模中板条梁的宽度取值为 0.04 m,并且沿着宽度方向仅划分一个网格.通过模态分析,得到各阶模态的振型、固有频率、广义质量和广义刚度信息,如图4和表1所示.本文仅列出前5阶振型. 图4 模态振型Fig.4 Mode shapes 表1 模态信息Tab.1 Modal information 对本文方法中涉及到的楔形体网格离散数目和计算模态数目进行收敛性分析.将楔形体的斜边分别离散为100、200和400等份进行计算,用于计算的模态数目为前5阶模态,时间步长为 4.0 μs,得到楔形体斜边中心位置处沿着斜边法线方向的振动位移如图5所示.图中:m为楔形体的网格离散数目;w为振动位移.可以看出,不同网格密度下的振动响应十分接近,200与400等份之间的最大位移响应偏差为 0.077%.将楔形体的斜边离散为200份,计算的模态数目为前5阶模态,时间步长Δt分别取值为 4.0、2.0 和 1.0 μs,得到楔形体斜边中心位置处沿着斜边法线方向的振动位移如图6所示.可以看出,不同时间步长下的振动响应十分接近,4.0 μs与 1.0 μs对应的最大位移响应偏差小于 0.001%.将楔形体的斜边离散为200份,时间步长取值为 4.0 μs,用于计算的模态数目分别为前1、3和5阶模态,得到楔形体斜边中心位置处沿着斜边法线方向的振动位移如图7所示.可以看出,不同计算模态下的振动响应十分接近,前3阶与前5阶计算模态的最大位移响应偏差为 0.083%. 图5 网格密度的收敛性Fig.5 Convergence of mesh densities 图6 时间步长的收敛性Fig.6 Convergence of time steps 图7 模态数目的收敛性Fig.7 Convergence of mode numbers 总体看来,本文算法具有较好的网格收敛性和模态收敛性.后续将斜边划分为200等份,并取前5阶振动模态用于计算. 图8 解耦结果的比较Fig.8 Comparison of decoupling results 图9所示为本文方法与文献 [9] 的计算结果的对比.可以看出,本文方法不仅可以求解流动分离前的结构变形,而且也可获得流动分离后的振动响应. 与基于Wanger砰击模型的计算结果相比,本文方法与利用CFD方法求解流场的计算结果更为接近.总体看来,本文方法可以应用于弹性楔形体入水冲击响应的分析. 图9 本文方法与文献结果的对比Fig.9 Comparison of this method with the literature results 为分析流固耦合作用的影响,进行不同冲击速度下弹性楔形体入水冲击响应的解耦方法和耦合方法的对比计算,结果如图10所示.图中,楔形体参数为4.1中的计算模型,比较对象为楔形体中间位置沿着法向方向的位移.可以看出,在低速状态下,解耦方法和耦合方法在流动分离前的结构响应比较接近(见图10(a)),而流动分离后两者存在明显不同,主要由于流动分离后结构的自身振动响应其主要作用,解耦方法未考虑流体的附加质量,以干模态下的固有频率振动,而耦合方法考虑了附加质量的影响,将以湿模态固有频率进行振动.随着冲击速度的增加,在流动分离前的阶段,2种方法计算结果也将出现明显差别.定义wDC和wC分别为解耦和耦合方法的位移响应峰值,如图10(d)和表2,在某些冲击速度范围内,解耦方法的最大位移响应小于耦合方法;而在某些冲击速度范围内,解耦方法的最大位移响应大于耦合方法,表明十分有必要采用合理的考虑弹性效应的耦合方法来分析结构的入水冲击响应. 图10 不同冲击速度下解耦与耦合方法的比较Fig.10 Comparison between decoupling and coupling methods under different impact velocities 表2解耦方法和耦合方法位移响应峰值的比较 Tab.2Comparisonofdisplacementresponsepeakvaluebetweendecouplingandcouplingmethods V/(m·s-1)wDC/mmwC/mm|wC-wDC|wC%20.363470.361590.5241.55631.51782.5452.41112.31754.0463.53943.41483.6574.98885.21694.3786.67097.495411.00 本文基于对半解析砰击模型、弹性结构的广义力和耦合动力方程的研究,系统地建立了弹性楔形体入水冲击的流固耦合分析方法.研究得到结论如下: (1) 通过对比不同网格密度、时间步长和模态数目下的计算结果,验证了该方法的收敛性. (2) 通过与商业软件结果、文献结果的对比,表明该方法可用于冲击过程中解耦和耦合响应的预报.而且与基于Wagner模型的水弹性分析方法相比,该方法不仅能够合理地预报流动分离前的结构响应,而且能够反映出流动分离后的振荡响应. (3) 采用耦合方法和解耦方法对比分析不同冲击速度下楔形体的结构响应,表明在弹性结构入水冲击分析时应合理地考虑流固耦合的影响,而本文方法可为该问题的分析提供参考.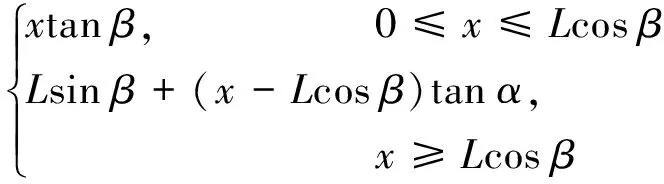
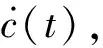


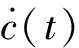
2 弹性体周围的压力场与广义力
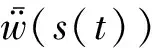
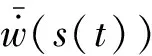


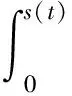


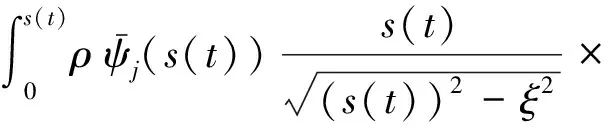

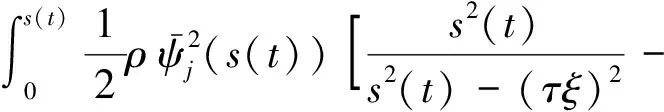
3 流固耦合方程的建立与求解
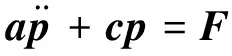
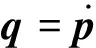
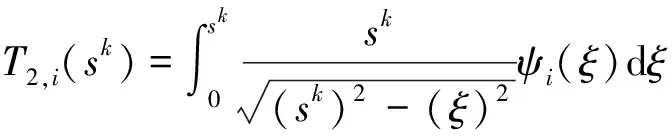
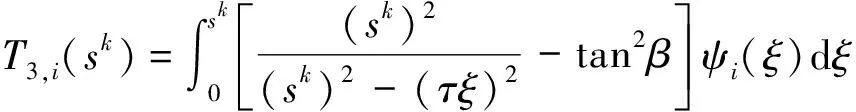
4 算法分析
4.1 计算模型

4.2 收敛性分析
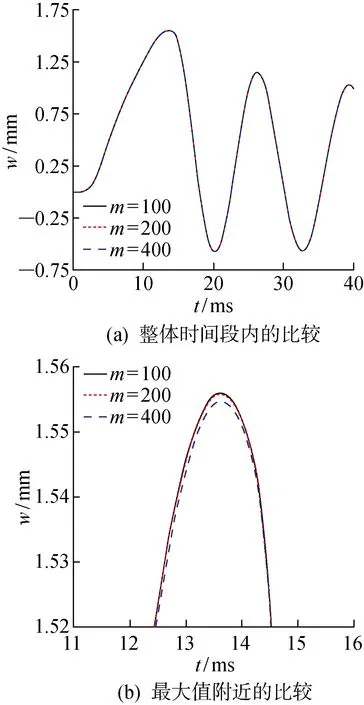
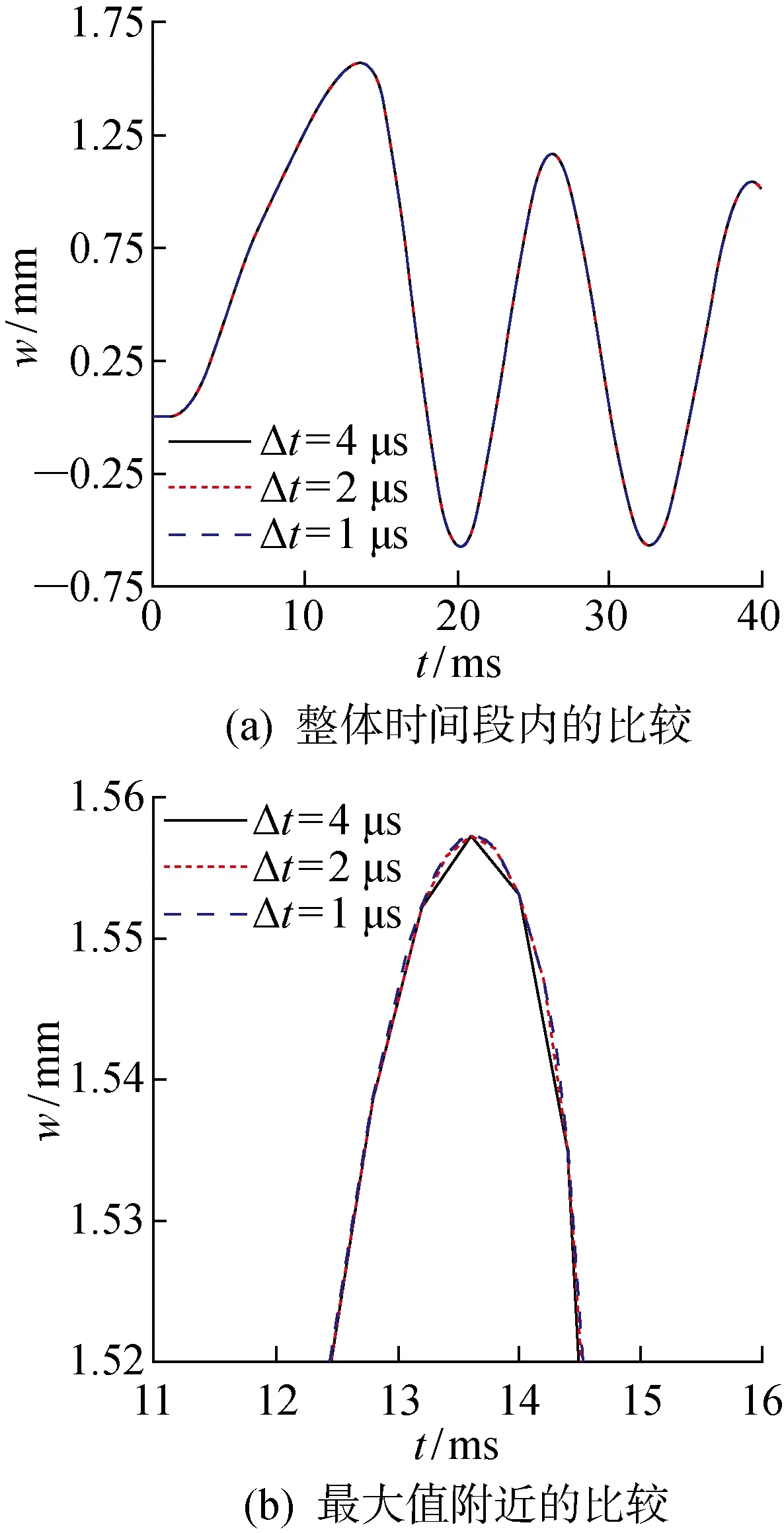
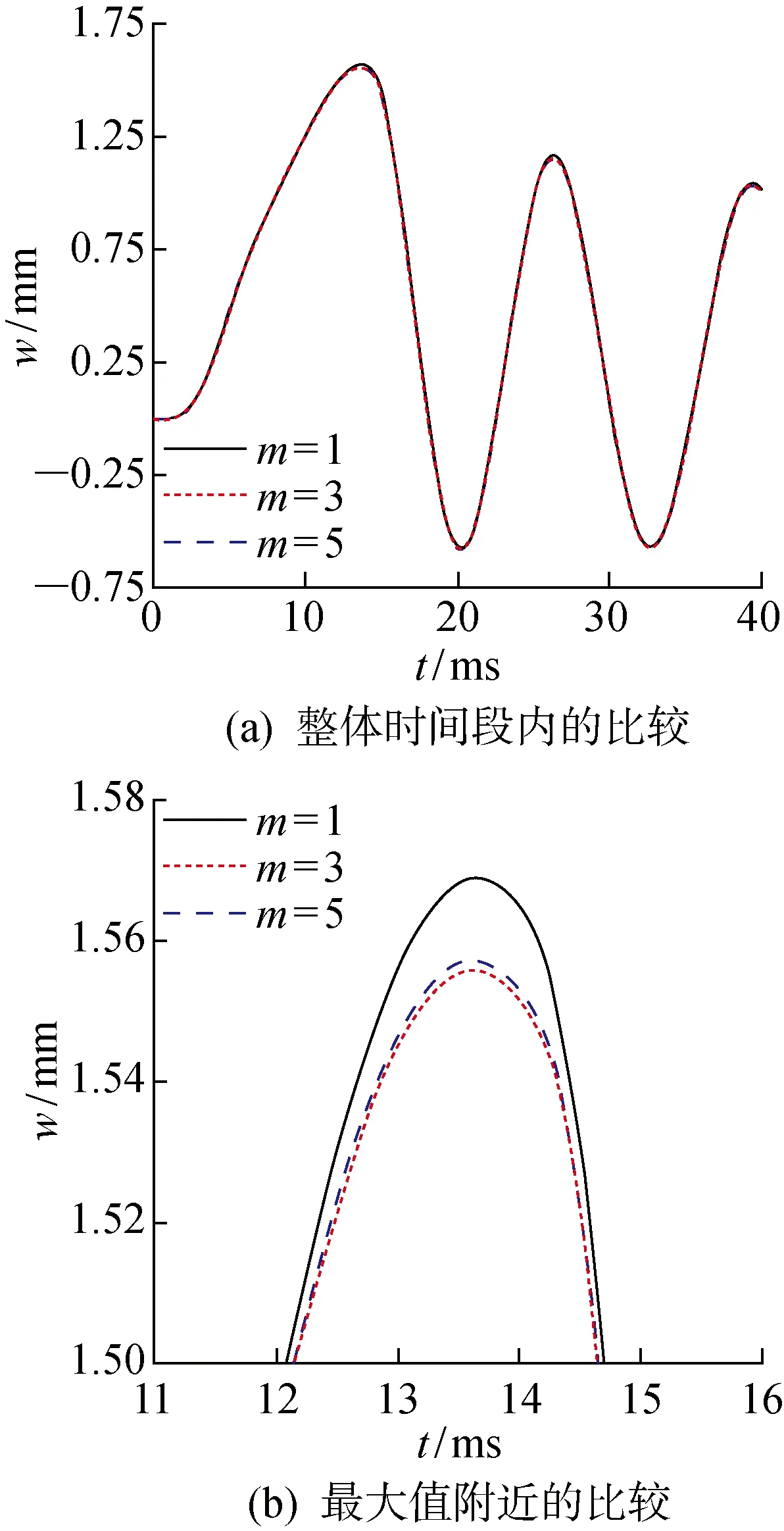
4.3 算法验证
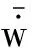

5 流固耦合的影响分析
6 结论
——工程地质勘察中,一种做交叉剖面的新方法

